1. Background
Percutaneous diagnostic and therapeutic procedures are commonly used in the treatment of axial and radicular spinal pain. The success of these procedures depends on the accuracy of needle placement. An assortment of needle types has been developed with a variety of tip shapes. The disparate needle designs play an integral role in determining the extent of needle deflection, accuracy of needle trajectory and, ultimately, in placement of the injectate at the intended target. Needle deflection can be controlled and utilized to correct for needle misalignment or to access non-collinear targets, and is commonly known as needle steering. Further understanding of the precise degree of deflection of each needle type has the potential to aid clinicians in improving needle steering and target accuracy by selecting the appropriate needle for their needs.
Based on limited studies of needle deflection, beveled spinal needles (e.g. Quincke) tend to deflect away from the beveled surface and notch located on the hub and the degree of deflection is related to gauge and depth of insertion (1, 2). Pencil-point needles (e.g. Whitacre) generally minimally deflect in the direction of the distal injection orifice (1). Epidural needles (e.g. Tuohy) tend to deflect toward the notch on the hub and beveled surface, in the direction of the curved tip (3). Thus far, studies have used porcine (1, 2, 4), polystyrene foam (5), and Plastisol (polyvinylchloride suspension) (6, 7) tissue simulants.
Ballistic gel, composed of collagen derived from animal tissue, has been well established as a tissue simulant, as it has a similar density and viscosity to human muscle tissue (8). While having similar physical properties to human muscle tissue, ballistic gel does not contain the heterogeneous properties of muscle (e.g. fascial planes), which can further impact needle deflection (9). The rationale behind using polystyrene foam is not discussed by Ahn et al. (2002) (5). Although polystyrene has been used as an ingredient in other tissue simulants, to our knowledge polystyrene foam has not been validated for this purpose. Additionally, Plastisol is produced by adding a softener to plastic, creating a polyvinylchloride suspension. The ingredients necessary to produce Plastisol are less accessible and the process is more complex when compared to ballistic gel (10). This study is the first experiment known to the authors of needle deflection using a ballistic gel tissue simulant.
2. Objectives
The purpose of this study is to further examine and quantify the deviation of commonly used spinal needles based on needle tip design and gauge, using a ballistic gel tissue simulant.
3. Materials and Methods
Six needles commonly used in spinal procedures were selected. Three beveled spinal needles (Quincke, Short Bevel, Chiba), two epidural needles (Tuohy, Hustead), and one pencil-point needle (Whitacre) were used in this study (Becton, Dickinson and Company, Franklin Lakes, NJ). 25-gauge (Quincke, Short Bevel, Whitacre), 22-gauge (Quincke, Short Bevel, Tuohy, Whitacre, Chiba), and 18-gauge (Hustead) needles were tested.
3.1. Gel Preparation
Ballistic gel samples were made from an 11% by mass 250 bloom Knox gel (Kraft Foods Group Inc, Northfield, IL). The mixture was made with eight ounces of gel mix and 64 ounces of 40° C filtered water stirred slowly to dissolve all the particles and to minimize the formation of air bubbles. This yielded a uniform consistency of all gel samples that were then poured into cylindrical aluminum molds. A total of 20 gel molds were made (10 with 80 mm depth and 10 with 40 mm depth) from a single batch of gel mixture. It was vital that the solution be poured into the molds in a very slow and deliberate manner to avoid frothing of the solution and air bubbles clinging to the mold. Ballistic gel requires a storage temperature of approximately 10° C. The ballistic gel specimens were made one day prior to the experiment trials. This was done because the physical properties of ballistic gel tend to change within 48 hours of curing, as the gel begins to dehydrate and harden.
Ballistic gel samples were made in aluminum molds of two depths, 40 mm and 80 mm respectively. The 40 mm mold had a volume of 82 milliliters and a radius of 26.8 mm, while the 80 mm mold was composed of a 164 mL volume gel. All molds were made from the same gel solution.
3.2. Drill Press Mount
The drill press (also known as a pedestal or bench drill) was used in order to ensure accurate and uniform needle trajectory into the ballistic gel sample. The set up comprised of a base, column (pillar) and spindle with an upright and a movable grip controllable by a handle. Handles radiating from a central hub moved the spindle vertically parallel to the axis of the column. The drill press used was RYOBI Drill (One World Technologies, Inc., Anderson, SC) with five-inch excursion of the spindle (Figure 1). The angle of the spindle was fixed relative to the table allowing consistent and accurate trajectory.
3.3. Needle Placement
Each needle was mounted in a drill press in order to ensure accurate needle trajectory into the ballistic gel sample. A level was used to align the needle vertically to the gel and after each needle was positioned, a bubble level was used to ensure accurate vertical positioning of the needle. The needle was secured to the grip and driven down to the center of the graph paper, piercing it (Figure 2A).
The gel mold was positioned underneath the needle and again the lever arm was lowered. The graph paper was again pierced and the distance between the two holes was measured using a digital caliper. This was repeated on two gels of different heights (40 mm and 80 mm) in order to obtain three points along the needle trajectory. This step was repeated four times for each needle, rotating the needle 90 degrees each time (Figure 2B).
3.4. Data Collection and Analysis
The point at which the needle entered the gel was considered (0,0), as there was no deflection at depth of zero millimeters. Using the shorter 40 mm ballistic gel mold, the distance away from midline at which the needle pierced the graph was termed (X, 40). Finally using the taller 80 mm gel mold, the distance was again measured and this point was termed (X, 80). This step was repeated four times with each needle through two different gels. Taking the mean of these data points and using 3 points, linear and parabolic curves were constructed for each needle. The comparison of deflection between all 22-gauge needles was analyzed using ANOVA test. Similar needles of different gauge size were analyzed using a t-test
4. Results
Each type of needle passed through both the 40 mm and 80 mm gels and distance of deflection away from midline was recorded. Individual passes for 40 mm and 80 mm gels can be found in Tables 1 and 2, respectively. Mean needle deflection data is recorded in Table 3.
| Needle Pass | Needle Deflection (mm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Chiba (22 g) | Quincke (22 g) | Quincke (25 g) | Short Bevel (22 g) | Short Bevel (25 g) | Hustead (18 g) | Tuohy (22 g) | Whitacre (22 g) | Whitacre (25 g) | |
| 1st Pass | 2.79 | 3.06 | 3.28 | 2.95 | 5.48 | 1.78 | 2.86 | 0.74 | 0.79 |
| 2nd Pass | 2.23 | 3.11 | 5.07 | 2.97 | 5.38 | 1.55 | 2.82 | 0.00 | 0.58 |
| 3rd Pass | 2.22 | 2.19 | 5.29 | 3.37 | 5.35 | 1.71 | 3.07 | 1.05 | 0.57 |
| 4th Pass | 2.30 | 3.03 | 5.11 | 3.04 | 5.97 | 1.46 | 3.11 | 0.98 | 0.57 |
Individual Needle Passes in 40 mm Gel Deptha
| Needle Pass | Needle Deflection (mm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Chiba (22 g) | Quincke (22 g) | Quincke (25 g) | Short Bevel (22 g) | Short Bevel (25 g) | Hustead (18 g) | Tuohy (22 g) | Whitacre (22 g) | Whitacre (25 g) | |
| 1st Pass | 6.70 | 8.84 | 11.79 | 8.92 | 15.58 | 4.01 | 7.86 | 0.56 | 0.36 |
| 2nd Pass | 7.06 | 8.70 | 12.45 | 10.75 | 16.30 | 4.52 | 7.49 | 1.20 | 1.36 |
| 3rd Pass | 9.32 | 8.90 | 12.16 | 9.95 | 15.63 | 4.71 | 7.56 | 0.42 | 0.57 |
| 4th Pass | 7.75 | 9.10 | 12.74 | 10.23 | 14.87 | 4.41 | 7.64 | 0.74 | 1.13 |
Individual Needle Passes in 80 mm Gel Deptha
| Needle Type | Mean Deflection ± SD (mm) | |
|---|---|---|
| 40 mm Depth Gel | 80 mm Depth Gel | |
| Chiba (22 g) | 2.39 ± 0.27 | 7.71 ± 1.16 |
| Quincke (22 g) | 2.85 ± 0.44 | 8.89 ± 0.17 |
| Quincke (25 g) | 4.69 ± 0.94 | 12.29 ± 0.41 |
| Short Bevel (22 g) | 3.08 ± 0.20 | 9.96 ± 0.77 |
| Short Bevel (25 g) | 5.55 ± 0.29 | 15.60 ± 0.58 |
| Hustead (18 g) | 1.63 ± 0.15 | 4.41 ± 0.30 |
| Tuohy (22 g) | 2.97 ± 0.15 | 7.64 ± 0.16 |
| Whitacre (22 g) | 0.69 ± 0.48 | 0.73 ± 0.34 |
| Whitacre (25 g) | 0.63 ± 0.11 | 0.86 ± 0.47 |
Mean Deflection of Spinal Needles in Ballistic Gels of Different Depths
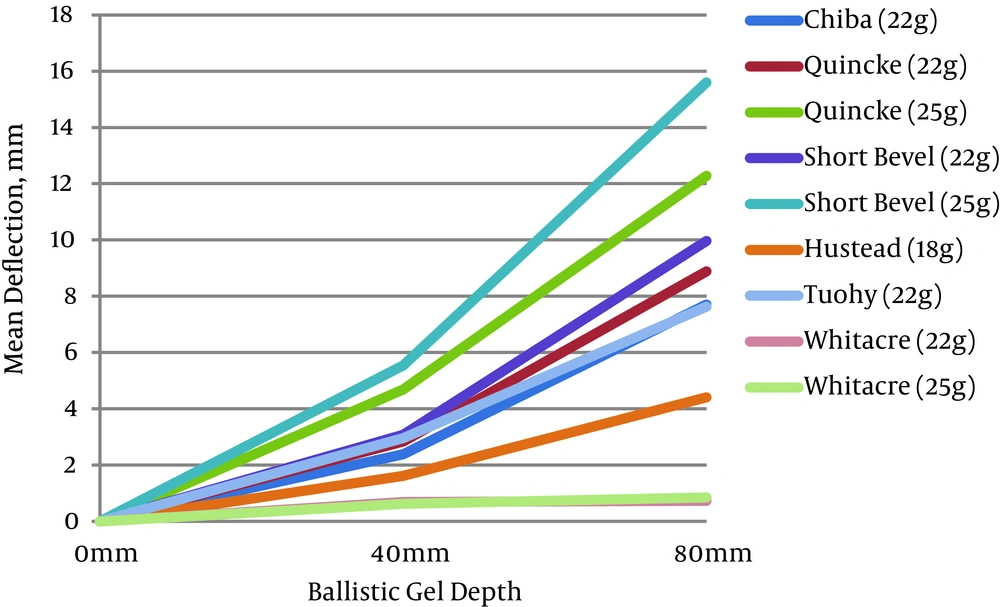
In comparing the mean deflection of 22 gauge needles of all types at 80 mm of depth, deflection was greatest among beveled needles [Short Bevel (9.96 ± 0.77 mm), Quincke (8.89 ± 0.17 mm), Chiba (7.71 ± 1.16 mm)], moderate among epidural needles [Tuohy (7.64 ± 0.16 mm) and least among the pencil-point needles [Whitacre (0.73 ± 0.34 mm)] (Table 4). A similar pattern was present at the 40 mm depth, but with less deflection. Deflection of each needle through 40 mm and 80 mm ballistic gel depths is graphically displayed in Figure 3. The greatest amount of deflection among all needles was seen with the 25 g Short Bevel needle (15.60 ± 0.58 mm), followed by the 25 g Quincke needle (12.29 ± 0.41 mm).
Increased gauge (i.e. thinner diameter needles) led to a statistically significant increase in deflection at 80 mm of depth among beveled needles [Quincke and Short Bevel (P < 0.001)], but not among pencil-point needles (P = 0.681) (Table 5).
| Needle Type | Mean Deflection ± SD (mm) | |||
|---|---|---|---|---|
| 40 mm Depth Gel | P | 80 mm Depth Gel | P | |
| Quincke | 0.012 | < 0.001 | ||
| 22 g | 2.28 ± 0.44 | 8.89 ± 0.17 | ||
| 25 g | 3.75 ± 0.94 | 12.29 ± 0.41 | ||
| Short Bevel | < 0.001 | < 0.001 | ||
| 22 g | 2.47 ± 0.20 | 9.96 ± 0.77 | ||
| 25 g | 4.44 ± 0.29 | 15.60 ± 0.58 | ||
| Whitacre | 0.801 | 0.681 | ||
| 22 g | 0.55 ± 0.48 | 0.73 ± 0.34 | ||
| 25 g | 0.73 ± 0.34 | 0.86 ± 0.47 | ||
A Comparison of Deflection Between Different Gauges of the Same Needle Typea
Of note, aside from the pencil-point needles, the least deflection was seen with the largest diameter needle studies, the 18 g Hustead epidural needle (4.41 ± 0.30 mm).
The direction of deflection of all beveled and epidural needles was reproducible, away from the bevel with Quincke, Chiba and Short Beveled needles and toward the tip curve of the Tuohy and Hustead epidural needles. Deflection of the Whitacre pencil-point needle was minimal, but it was not uniform and did not follow a similar pattern.
5. Discussion
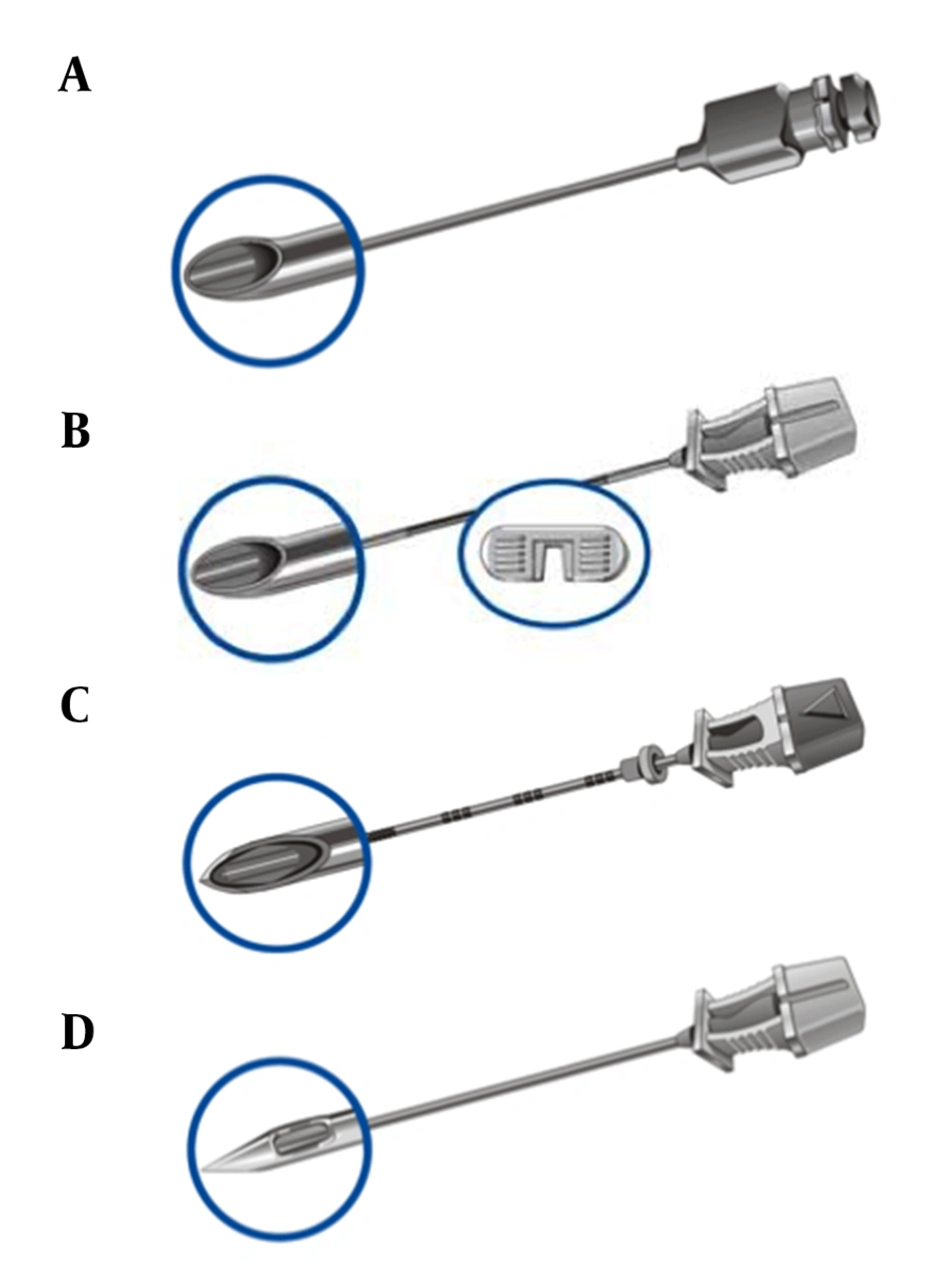
Our data confirms multiple inherent principles with regard to needle steering and deflection. The use of ballistic gel in our model created a homogenous medium to accurately assess needle deflection without the potential bias introduced by animal facial planes that may be present in porcine or bovine injection models. Collectively, beveled needles (Quincke, Short Bevel, Chiba) behaved predictably and consistently. Beveled needles deviate away from the notch (and thus bevel) toward the longer end of the needle. Consistent with Newton’s third Law, is the generation of a force by the gel medium perpendicular to the beveled surface of each needle. Force can be broken down into component vectors. As such, the gel medium produced a force vector directed back along the axis of the needle, as well as another force perpendicular to the beveled side of the needle directing it toward its longer end, away from the bevel opening.
Tuohy needles in contrast behave differently when compared to beveled needles (Figure 4A). Tuohy needles have a curved side with the bevel opening perpendicular to the length of the needle to the side opposite the curve. Therefore, as the needle is advanced, there is little contribution from the bevel opening to generate a perpendicularly directed force vector. More so contributing to a perpendicularly directed force vector is the curved portion of the needle. The force the gel medium imparts back onto the curve as the needle is advanced generates component vectors, with the perpendicularly directed vector component causing needle deviation away from the curve of the needle or toward the bevel opening and notch on the hub.
The Hustead needle has some structural similarities to the Tuohy in that there is a bevel side and curved side to the needle (Figure 4B). It is structurally different in that the beveled end is angled relative to the long axis of the needle and therefore the curve does not extend as far as in the Tuohy. Force vectors therefore are generated perpendicular to the length of the needle by both the curve and the bevel. The curved portion of the needle generates a perpendicularly directed force towards the bevel, whereas the bevel generates an opposing perpendicular force. Our data demonstrates that in the case of the Hustead needle, the curve does more to direct the needle than the bevel. One might further consider that the curve effect on needle deflection is countered by that of the angled bevel, minimizing the overall extent of needle deflection. Indeed, we do see less deflection with the Hustead as compared to the Tuohy, but it is unclear if this disparity is actual a result of varying needle gauges. More research is needed to directly compare needles of equal gauge with respect to the Hustead and Tuohy needles.
It is evident from our data that irrespective of bevel orientation and curve, needles deflect more when they are thinner (i.e. of higher gauge). Thinner needles, therefore may be more difficult to maneuver when a straight trajectory is desired, but offer more flexibility with regard to maneuverability at greater depth. In a practical sense however, thinner needles are more likely to be deflected by fascial planes. Needle thickness influences final placement via a compromise of maneuverability and what the authors have termed “deflect-ability”.
Hooke’s law is used to describe the elastic properties of metal under different forms of stress. Hooke’s law represents a linear relationship between the degree of deformation and force of an elastic coefficient specific to the material being investigated. The amount of force needed to deviate an object - in this case, a needle - would be directly related to the elastic coefficient of the specific needle being evaluated. Each of the beveled needles in question would, therefore, have varying elastic coefficients that would consistently allow for varying degrees of deviation during needle advancement. However, as seen in the data, this deviation increases in nonlinear fashion as depth of advancement increases from 40 mm to 80 mm. Therefore, the elastic coefficient of each respective needle alone cannot explain the extent of our observed needle deflection. One possible explanation for this finding is material non-homogeneity or anisotropy of the ballistics gel.
Our data indicates that the short beveled spinal needle had the greatest degree of deflection of all the beveled needles. The angle of the bevel of the short beveled spinal needle and area of force are such that the force vector directed perpendicularly along the axis would be smaller than that of the Quincke (Figure 4C) and Chiba needles with similarly force magnitudes directed from the hub. The force vector directed parallel to the length of the needle, however, would be greater with the short beveled spinal needle. The authors, therefore, hypothesize that the extent of deflection, therefore, is dependent on the ratio of these two (vertically and perpendicularly directed) force vectors. Specifically, a shallower bevel would generate more resistance to advancement along the gel medium and therefore allow greater deflection of the needle perpendicular to the direction of its advancement.
Furthermore, this hypothesis regarding the ratio of these force vectors may explain in part why the degree of needle deflection followed a nonlinear distribution as depth of advancement is increased. As the needle is advanced and the degree of deflection increased, the bevel opening would come more in line with the direction of needle advancement. This, in effect, would generate more resistance to advancement allowing greater deflection away from the bevel opening. The Chiba, which is a cutting needle, would have the least resistance to needle advancement and therefore deviate the least as seen in our data. Likely contributing to this nonlinear relationship is also the developing curve of the needle itself as it is advanced. The curve as we know from the Tuohy also generates a force vector. The bevel in the instance of the Chiba, Quincke and short beveled needles would have an additive effect to the developing curve as opposed to the negligible and opposing force seen in the Tuohy and Hustead needles, respectively.
Pencil point needle types demonstrated the least movement of all the needle types with minimal deflection after advancement through the gel medium. There was no evidence of reproducibility with regard to direction of deflection as well as the orientation of the orifice opening. Minimal deflection among pencil point needles is consistent with prior studies (1, 2, 4); however, Sitzman et al. demonstrated that the minimal deflection was found toward the bevel or orifice, whereas in our study this was not seen (1). The Whitacre (Figure 4D), therefore, in a homogenous medium would have the greatest predictability with regard to trajectory, but in a heterogeneous medium as in the human body would have the least steerability if deflection from the desired trajectory occurred. Pencil point needles would therefore have the least utility to reach a specific target in a heterogeneous medium as would occur in vivo.
This study did have several limitations. While conceptually, the use of ballistic gel was intended to create a homogenous medium to accurately assess needle deflection, in reality there was likely tissue anisotropy. This study aims to address these confounding variables that would affect needle deflection and steerability properties that would occur in a heterogeneous medium (e.g. tissue planes, fascial layers, scarring, etc.). Additionally, this study was small in terms of number of needle passes collected. More data could be collected to increase the power of the study. Furthermore, though needles varied with regard to gauge and bevel type, there are additional factors at play that can affect elastic coefficients. This may include metal hardness, wall thickness, and industrial preparatory factors that play a role in the intrinsic elastic coefficient of different needle types irrespective of the bevel and/or curve at the end of the needle. In order to most accurately assess the effect of curve and bevel on needle deflection, consistent coefficients of elasticity for similarly gauged needles of different types are necessary.
Our findings confirm that gauge and shape of the needle tip play a crucial role in determining the degree and direction of deflection (1-4). Clinically utilizing this information, when a procedure requires a needle to be steered around obstacles, or along non-collinear targets, the predictable and large amount of deflection obtained through use of a beveled spinal needle may prove beneficial. On the other hand, when minimal deflection is desired, a pencil-point or large diameter (small gauge) needle may be the most appropriate selection. These findings are also significant in the case of obese patients, where the increased tissue depth required to reach a target successfully may cause a greater degree of deflection.