Abstract
Keywords
Cognitive Evolution Exploration Spatial Cognition Spatial Navigation Recapitulation Logic of Neural Network Group Theory Primate Rodent
1. Introduction
The comparative analysis of cognitive development has demonstrated that the prerequisites and/or outcomes for the same task may differ across species (1). Povinelli (2) also proposes that cognitive processes underlying a behavior might differ from one species to another. In a recent article, Nemati (3) entertained the notion that parallel mathematical descriptions of behavioral structures in humans and other species does not necessarily lead to parallel cognitive outcomes.
Thus, following the notion that further analysis is always necessary to determine whether parallel mathematical description of two events actually represents the same phenomenon (4), more examinations of the mechanisms that may lead to the construction of the parallel behaviors has been suggested recently (3). One way of doing so as Penn et al. (5) have pointed out in discussing Darwin’s mistake in portraying the difference between human and nonhuman mind as a quantitative rather than a qualitative one, is the challenging task of explaining how functional discontinuity between the two could be realized biologically. In line with Nemati’s (3) recent analysis, the present study first examines Piaget’s version of recapitulation theory and then examples of brain areas that might be involved in generating superficial parallel structures in spatial navigation will be examined and finally a theoretical framework will be sketched to account for the superior cognitive competence in humans.
Building upon the characteristics of Georg Cantor’s transfinite arithmetic in relation to elementary arithmetic in establishing a non-contradiction status in a system, which was proved by Kurt Godel’s incompleteness theorems to be impossible by means available to the system itself, Piaget’s (6) description of “reflective abstraction” of logico-mathematical structures during development enriched his version of recapitulation theory (ontogeny repeats phylogeny). In his view, such structures bring about the equilibrium of assimilation and accommodation that function consistently throughout the evolution and development of cognition. In the present study, Piaget’s view of the evolutionary transition from action to cognition via abstraction of logico-mathematical structures is evaluated in a “thought experiment”. It will be demonstrated that when dealing with a specific, innate and highly structured behavior (i.e. exploratory excursions), the behavior can be represented “evolutionarily” as a group of integers modulo n by the set {0,1,2,…, n-1} and by the symbol (Z, +) in rats but not in humans (cf. 3 for the examples of parallel structure of behavior). Following the conclusion of the thought experiment, the role that distinct brain areas may play in generating a superficial parallelism in behavioral structure across species will be discussed and finally a theoretical framework will be presented to explain how humans might have achieved such a superior cognitive competence despite lacking the same level of mathematically structured (innate) behaviors.
2. Arguments
2.1. A Thought Experiment on Piaget’s Version of Recapitulation
The thought experiments have been undeniably useful tools in the development of philosophical arguments as well as facilitating scientific discoveries (7). The application of thought experiments might be even more relevant when dealing with the evolution of cognition for which experimental manipulations are virtually impossible. The following “thought experiment” will demonstrate the logical difficulty in the acceptance of Piaget’s version of recapitulation across species. In this thought experiment it is assumed that a mathematician with no formal training in advanced mathematics1 could infer all the axioms by just looking at the behavior, were there the right ingredients in the behavioral repertoire of either rats or humans in the following two tasks: In the first scenario our mathematician lives in the real world and observes the movements of organisms (i.e. rats, humans etc.). In the second scenario, our mathematician is assumed to play the role of species’ computational system living within the brain of different species (i.e. rats, humans etc.) and observing the species’ behavior over the course of evolution.
2.2. Scenario 1
Imagine our mathematician was asked to observe the exploratory behavior by rats or by humans separately after each entered in an open field. Note that the experiment is conducted in a room devoid of any cues that shape the exploratory path in a certain form. The question then would be “What axioms would the mathematician infer from those behaviors and how would he/she go about the proof of the first theorem?”
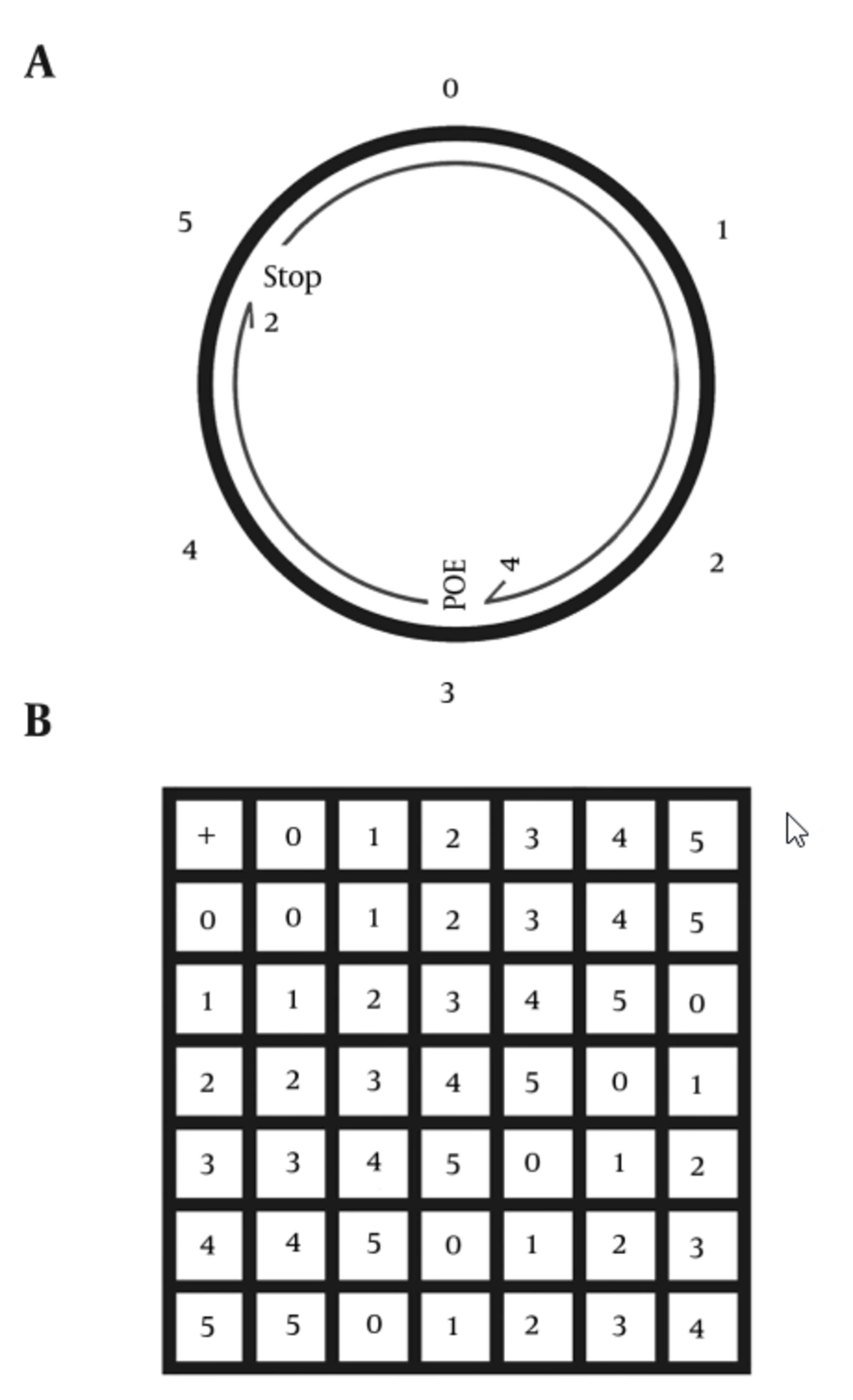
Basically, the mathematician would observe that rats use various spatial strategies to return to the point of entry (POE) on a circular open table. They might reach the POE via a clock or counter clock-wise locomotion along the edge of the table or they might take a shortcut (3). Our mathematician would not observe such an organization of exploratory locomotion to any innately defined place by humans. Thus, for example as a result of observing a rat (not a human) that moves clockwise in a circuitous path from POE to POE, our mathematician would be able to form a group of integers modulo n (i.e. Z6) table (Figure 1) whose correspondence to the laws of group would be testable (8, 9). Because all the axioms can be inferred from the pattern of exploration by rats, it would be possible to prove the first theorem in which ab = ac or ba = bc implying that b = c.
Return to the POE and the Group of Integers Modulo n
2.3. Scenario 2
Now imagine that there is a mathematician that plays the role of a computational system within the brain of each member of different species and the logico-mathematical operations in a particular species can be the result of the inference made by this mathematician from their behavior over the course of evolution. Our observation to this date implies that unlike the observation made in the first scenario, the “biological” mathematician in the rat’s brain has not been able to derive any theorems by observing the behavior from the view of a first person.
Now the question is “Why has the biological mathematician within the human brain done so much better in deriving all the theorems and subsequent mathematics (at the cognitive level) despite the lack of such highly structured innate behaviors (found in other species, i.e. rats) from which the related axioms is expected to be abstracted? “Why the accommodation process has led to more behavioral subsystems in rodents as is expected from Piaget’s version of recapitulation but not to more sophisticated cognitive subsystems?”
2.4. The Brain and the Structure of Behaviour
A more careful analysis indicates that distinct computational processes realized by different brain areas across species may generate parallel (innate and/or learned) behavioral structures. For instance, the concept of shortcuts is the most intimate link to the concept of cognitive map developed as a result of an experiment by Tolman (10). However, the cognitive map is assumed to support other spatial strategies including the circular excursions on an open table etc. (i.e. excursions like the ones discussed in the thought experiment) via the active function of neural ensembles in the hippocampus and related areas (11-13). Although, the concept of cognitive map is a key in understanding spatial cognition (14), spatial navigation has been theorized to be mediated by landmarks and/or movement-related cues in a number of species (15-18) including humans (19). Consistent with the importance of landmarks in guiding spatial navigation either as the only source or in combination with cognitive mapping process, other variables (i.e. scanning, reorientation etc.) associated with locomotion may also play important roles in gathering information for a successful performance of navigational tasks (20, 21). The main underlying argument of the section is that each of these contributing factors may be a product of different but functionally parallel neuroanatomical channels in different species. The possibility of such channels will be briefly discussed with respect to two major sources of navigation in the following examples:
Visual orientation: according to the Schneider’s (22) well-known dichotomy of two visual systems, the tectal and geniculostriate pathways are responsible for the localization and identification of objects in the visual field, respectively. However, further investigations cast doubt on the reliability of this dichotomy (23-26). Among these investigations, Milnar and Goodale (27) provided the evidence for the parallel sensorimotor channels including both the tectal and geniculostriate pathways that serve as the neuroanatomical basis of visually guided locomotion. Interestingly, they argued for the modulatory effect of geniculostriate system on tectal outputs. Considering the superior cortical development in humans, this might make a difference when explaining behaviorally parallel visual navigation across species.
Cognitive map: since the concept of cognitive map was introduced by Tolman (10), the discovery of place cells (28) and that of head direction cells (29) or grid cells (30) have contributed to the theoretical formulation of significant solutions for the puzzle of the neural basis of such a map based on the concept of path integration by rats (11). However, Shrager et al. (31) have argued that the path integration might be supported by the well developed neuocortex in humans while the hippocampus and entorhinal cortex may play more important role in rodents. Such distinctions will clearly introduce the possibility of two parallel but different neuroanatomical bases for parallel structures of spatial navigation across species. The question that has remained unanswered is “What role such potentially different neural mechanisms may play in the construction of the superior cognitive functions in our species?” A theoretical framework will be presented to introduce a potential way of explaining the mechanism of such superiority.
2.5. A Theoretical Framework
The logical difficulty experienced in reaching a parallel intellectual outcome throughout the “thought experiment” suggested that the notion of recapitulation cannot account for the evolution of cognition in all species equally. If the structure of innate behavior as the source of cognitive evolution in Piaget’s view does not explain the logico-mathematical competence, what would? In order to address this question, the present study will expand Piaget’s (6) welcoming approach to McCulloch’s (32) computational proposal of logical network of neuronal impulses by emphasizing on the role of nervous system in cognitive evolution as opposed to Piaget’s main thesis of the behaviour being the “motor of evolution” (33). As a result of such a theoretical redirection, the present study proposes that the neural encoding of the same behavioural structures in distinct brain areas across species may lead to both parallel behavioral but unparalleled cognitive evolutionary outcomes.
Consistent with McCulloch’s (32) computational proposal that the logical operations on inputs to an organism may well be a function of the binary nature of “All-or-None” activity of neurons in a neural network, and in order to explain the superior cognitive function in humans, here the focus is on the transition from logico-mathematical organization of behavior to that of cognition, based on the assumption that if the mathematician in the real world (scenario 1) can infer the logico-mathematical axioms from the behavior realized by the pattern of neuronal impulses, the same pattern of neuronal impulses can be used by the mathematician within the brain (scenario 2) to abstract the same axioms for further processing in other brain areas. In fact, the logico-mathematical axioms may correspond to abstracted patterns of operations embedded in the cortical neural activities of the brain areas that contributes to the realization of the structure of various spatial behavior built on the innate and/or learned behavioral components in humans. These abstracted forms of operations later will be reformulated symbolically (e.g. verbally) during the development of language as a foundation for the derivation of theorems from such axioms. The outcome may be used later as a more conscious strategy to solve spatial problems by humans. The followings are two sets of supporting studies:
- The activity of left frontotemporal and bilateral prietofrontal neural networks in humans have been shown to be associated with the “logico-mathematical” operations, specifically with the logical deduction and computations, respectively (34).
- The role of cortical areas in guiding spatial navigation (cf. 35 for the role of parietal cortex in abstracting spatial features) is proposed by Shrager et al. (31) to be dominant in humans (35).
In order to put this notion into perspective, the shortcut behavior can be examined in this new context. If the shortcut behavior is encoded in the cortical neural network of which parietal cortex may be the core, then humans are in a better position to abstract the logico-mathematical patterns of such cortical activities associated with the behavior (i.e. shortcut), and later during the evolution of language reformulate them in related brain areas. Thus, whether or not a problem in a behavioral task is solved based on transitive inferences and whether it indicates an operation in prepositional calculus (5, 36) may well depend on the brain area that has mediated the behavior over the course of evolution. Metaphorically, the mathematician within the human brain is sitting at the best site (i.e. cortex) to translate (abstract) the behavior related cortical activities into the axioms of group but the one in the rat’s brain cannot do the same, sitting in the hippocampus.
3. Conclusions
The comparative analysis of cognition that begins with behavioral commonalities (instead of differences) provides a common baseline to re-evaluate the differences in affiliated factors and consequent outcomes as a qualitative gap (instead of a quantitative one) between species. Based on the obvious lack of a comparable cognitive capacity between humans and non-humans, a definite example of parallel description of behavioral structure goes against the explanatory power of behaviour for cognition across species (at least in the framework proposed by Piaget cf 3).
The present analysis indicates that different species might demonstrate parallel behaviours while the underlying mechanism of each may stem from different computational processes, which might be realized by different brain structures. For instance, the dominant theory in explaining spatial navigation does not suggest the use of cognitive maps by insects (15). In addition, even when animals use the same spatial strategy (e.g. path integration) to solve a navigational problem, different mechanisms may be used by different species such as the insect vs. rat (11, 37). More specifically among mammals, rats might take a shortcut that is dominantly organized by the contribution of hippocampus and related areas (11, 14, 28) but this behavior maybe more dependent on the pattern of neuronal impulses in cortical areas in humans (31). Note that the influence of language on cognitive capacities makes a difference between humans and great apes even when these species begin with the same spatial reference frames (38, 39). Obviously, the contribution of language to the construction of human cognition is only possible based on a new set of computational and neuroanatomical variables (40), which makes a qualitative difference between humans and great apes a real possibility.
These variables play determining roles in generating different evolutionary cognitive outcomes from one species to another while they all may be able to solve the same problem in a behavioral task. In fact, the Achilles’ hill in our understanding of cognitive evolution may well be in our tendency to give a priority to behavior instead of paying enough attention to the division of labour in the brain and the role that various brain areas may play in producing such parallel behaviors. A question for the future studies then is about the validity of generalization of research findings across species especially generalizing from simpler species to humans, which would have strong implications for translational research in the fields that are concerned with human cognition such as psychology, psychiatry and neurology.
References
-
1.
Rosati AG, Wobber V, Hughes K, Santos LR. Comparative developmental psychology: how is human cognitive development unique? Evolut Psychol. 2014;12(2):147470491401200000.
-
2.
Povinelli DJ. Behind the ape's appearance: Escaping anthropocentrism in the study of other minds. Daedalus. 2004;133(1):29-41.
-
3.
Nemati F. From Parallel Mathematical Description of Action to Unparalleled Outcome of Abstraction: A Comparative Analysis. Arch Neur. 2015;2(4).
-
4.
Kuhn TS. The structure of scientific revolutions. University of Chicago press; 2012.
-
5.
Penn DC, Holyoak KJ, Povinelli DJ. Darwin's mistake: explaining the discontinuity between human and nonhuman minds. Behav Brain Sci. 2008;31(2):109-30. discussion 130-178. [PubMed ID: 18479531]. https://doi.org/10.1017/S0140525X08003543.
-
6.
Piaget J. Biology and knowledge: An essay on the relations between organic regulations and cognitive processes. Chicago: The University of Chicago Press; 1971.
-
7.
Nersessian NJ. Why do thought experiments work? Proceedings of the Cognitive Science Society. 1991.
-
8.
Pinter CC. A book of abstract algebra. Courier Corporation; 2012.
-
9.
Rotman JJ. Advanced modern algebra. 114. American Mathematical Soc; 2010.
-
10.
Tolman EC. Cognitive maps in rats and men. Psychol Rev. 1948;55(4):189-208. [PubMed ID: 18870876].
-
11.
McNaughton BL, Battaglia FP, Jensen O, Moser EI, Moser MB. Path integration and the neural basis of the 'cognitive map'. Nat Rev Neurosci. 2006;7(8):663-78. [PubMed ID: 16858394]. https://doi.org/10.1038/nrn1932.
-
12.
McNaughton BL, Barnes CA, Gerrard JL, Gothard K, Jung MW, Knierim JJ, et al. Deciphering the hippocampal polyglot: the hippocampus as a path integration system. J Exp Biol. 1996;199(Pt 1):173-85. [PubMed ID: 8576689].
-
13.
Sharp PE, Kubie JL, Muller RU. Firing properties of hippocampal neurons in a visually symmetrical environment: contributions of multiple sensory cues and mnemonic processes. J Neurosci. 1990;10(9):3093-105. [PubMed ID: 2398374].
-
14.
O'keefe J, Nadel L. The hippocampus as a cognitive map. Oxford University Press, USA; 1978.
-
15.
Cartwright BA, Collett TS. Landmark learning in bees. J Compar Physiol. 1983;151(4):521-43.
-
16.
Collett TS, Cartwright BA, Smith BA. Landmark learning and visuo-spatial memories in gerbils. J Comp Physiol A. 1986;158(6):835-51. [PubMed ID: 3735168].
-
17.
Hines DJ, Whishaw IQ. Home bases formed to visual cues but not to self-movement (dead reckoning) cues in exploring hippocampectomized rats. Eur J Neurosci. 2005;22(9):2363-75. [PubMed ID: 16262675]. https://doi.org/10.1111/j.1460-9568.2005.04412.x.
-
18.
Nemati F, Whishaw IQ. The point of entry contributes to the organization of exploratory behavior of rats on an open field: an example of spontaneous episodic memory. Behav Brain Res. 2007;182(1):119-28. [PubMed ID: 17590451]. https://doi.org/10.1016/j.bbr.2007.05.016.
-
19.
Wang R, Spelke E. Human spatial representation: insights from animals. Trends Cogn Sci. 2002;6(9):376. [PubMed ID: 12200179].
-
20.
Redish AD. Beyond the cognitive map: from place cells to episodic memory. MIT Press; 1999.
-
21.
Sinnamon HM, Karvosky ME, Ilch CP. Locomotion and head scanning initiated by hypothalamic stimulation are inversely related. Behav Brain Res. 1999;99(2):219-29. [PubMed ID: 10512588].
-
22.
Schneider GE. Two visual systems. Science. 1969;163(3870):895-902. [PubMed ID: 5763873].
-
23.
Harting JK, Hall WC, Diamond IT, Martin GF. Anterograde degeneration study of the superior colliculus in Tupaia glis: evidence for a subdivision between superficial and deep layers. J Comp Neurol. 1973;148(3):361-86. [PubMed ID: 4735378]. https://doi.org/10.1002/cne.901480305.
-
24.
Wurtz RH, Albano JE. Visual-motor function of the primate superior colliculus. Annu Rev Neurosci. 1980;3:189-226. [PubMed ID: 6774653]. https://doi.org/10.1146/annurev.ne.03.030180.001201.
-
25.
Albano JE, Wurtz RH. Deficits in eye position following ablation of monkey superior colliculus, pretectum, and posterior-medial thalamus. J Neurophysiol. 1982;48(2):318-37.
-
26.
Goodale MA, Foreman NP, Milner AD. Visual orientation in the rat: a dissociation of deficits following cortical and collicular lesions. Exp Brain Res. 1978;31(3):445-57. [PubMed ID: 648607].
-
27.
Mlinar EJ, Goodale MA. Cortical and tectal control of visual orientation in the gerbil: evidence for parallel channels. Exp Brain Res. 1984;55(1):33-48. [PubMed ID: 6745353].
-
28.
O'Keefe J, Dostrovsky J. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res. 1971;34(1):171-5. [PubMed ID: 5124915].
-
29.
Ranck Jr JB. Head-direction cells in the deep cell layers of dorsal presubiculum in freely moving rats. Soc Neurosci Abstr. 1984;10(176.12).
-
30.
Hafting T, Fyhn M, Molden S, Moser MB, Moser EI. Microstructure of a spatial map in the entorhinal cortex. Nature. 2005;436(7052):801-6. [PubMed ID: 15965463]. https://doi.org/10.1038/nature03721.
-
31.
Shrager Y, Kirwan CB, Squire LR. Neural basis of the cognitive map: path integration does not require hippocampus or entorhinal cortex. Proc Natl Acad Sci U S A. 2008;105(33):12034-8. [PubMed ID: 18687893]. https://doi.org/10.1073/pnas.0805414105.
-
32.
McCulloch WS, Pitts W. A logical calculus of the ideas immanent in nervous activity. 1943. Bull Math Biol. 1990;52(1-2):99-115. discussion 73-97. [PubMed ID: 2185863].
-
33.
Piaget J. Behavior and evolution. New York: Pantheon Books; 1978.
-
34.
Houde O, Tzourio-Mazoyer N. Neural foundations of logical and mathematical cognition. Nat Rev Neurosci. 2003;4(6):507-14. [PubMed ID: 12778122]. https://doi.org/10.1038/nrn1117.
-
35.
Poucet B, Benhamou S. The neuropsychology of spatial cognition in the rat. Crit Rev Neurobiol. 1997;11(2-3):101-20. [PubMed ID: 9209826].
-
36.
Davis H. Transitive inference in rats (Rattus norvegicus). J Comp Psychol. 1992;106(4):342-9. [PubMed ID: 1451416].
-
37.
Collett TS, Collett M. Path integration in insects. Curr Opin Neurobiol. 2000;10(6):757-62.
-
38.
Haun DB, Rapold CJ, Call J, Janzen G, Levinson SC. Cognitive cladistics and cultural override in Hominid spatial cognition. Proc Natl Acad Sci U S A. 2006;103(46):17568-73. [PubMed ID: 17079489]. https://doi.org/10.1073/pnas.0607999103.
-
39.
Gentner D. Spatial cognition in apes and humans. Trends Cogn Sci. 2007;11(5):192-4. [PubMed ID: 17383219]. https://doi.org/10.1016/j.tics.2007.03.002.
-
40.
Friederici AD. Pathways to language: fiber tracts in the human brain. Trends Cogn Sci. 2009;13(4):175-81. [PubMed ID: 19223226]. https://doi.org/10.1016/j.tics.2009.01.001.
-
41.
Debnath L. Srinivasa Ramanujan (1887-1920) and the theory of partitions of numbers and statistical mechanics a centennial tribute. Int J Mathematics Mathematic Sci. 1987;10(4):625-40.