The Calculation of the Uphill Energy Cost of Running from the Level Energy Cost of Running in a Heterogeneous Group of Mountain Ultra Endurance Runners

1. Background

The energy cost of running on level and on positive gradients has been extensively investigated (1, 2), and the place of Cr among ultra-endurance performance factors is still debated (3, 4). According to (2) and (5), uphill Cr in J.kg^-1.m^-1 or mLO₂. kg^-1.m^-1 can be calculated from level Cr, but Balducci et al. (2016) demonstrated that this statistical relationship could hide individual variations with a significant impact on the performance during mountain races (6) in a homogeneous group of high level mountain endurance runners. Indeed, it was found that uphill Crs at 25% and 12.5% grades (respectively Cr_25% and Cr_12.5%) were associated with each other (r = 0.78, P < 0.01) whereas level Cr was not associated with either Cr_25% or Cr_12.5% (r = 0.09 and r = 0.10). The fact that some runners have an inferior (greater) Cr in level running and a superior (lower) Cr in uphill running can be related to muscular and mechanical factors and other individual characteristics (7, 8). However, this absence of relationship was observed in a smaller group of runners (n = 10).

The aim of the present study was to determine if level and uphill Crs are correlated in a heterogeneous population of mountain runners, and if this relationship is strong enough to calculate uphill Cr from level Cr with di Prampero equation. We hypothesized that level and uphill Crs were correlated in this type of population and we evaluated the differences between the real and the calculated uphill Cr.

2. Methods

2.1. Participants

A total number of 24 healthy male and experienced mountain runners participated in this study (mean ± SD: age 41.7 ± 9.5 years, height 1.77 ± 0.04 m, mass 71.7 ± 5.5 kg, Body Mass Index 22.9 ± 1.3 kg.m^-2, V O₂ max 4.64 ± 0.36 m.s^-1). Subjects were recruited on a voluntary basis. They had to be classified by the International Trail Running Association, with at least one race in the Trail ultra L (70 to 99 km) or Trail ultra XL (> 100 km) category. Participants were healthy, without injuries, and were not taking any medication. Written informed consent was obtained from the participants, and the study was conducted according to the principles laid down in the Declaration of Helsinki. Project approval was obtained from the local ethics committee on human experimentation.

2.2. Procedure

Experiments were carried out in conjunction with the MUM (Interlacs Trail) which took place in Aix-les-Bains (France) in May 2016. The course was 80 km long with a total positive elevation of +3500 m and a total negative elevation of -3700 m. The study was conducted in three phases: pre-race testing one day before the race, MUM race, and the post-race testing within 15 minutes after the end of the race.

2.3. Energy Cost of Running

Under these conditions, two Crs were calculated in a randomized way, during two bouts of 5 minute durations under two slope conditions: 0% and 10%. Before the first measurement of the Cr, and in order to get accustomed to the treadmill, each subject performed a 15 minute warm-up at 50% of V O₂ max and 0% incline. Then the treadmill speed was set for each participant at 60% of V O₂ max. The treadmill used was a MTR-Runner srl (Cavezzo-Italy) with a working speed of 0.1 to 20 km/h, and an inclination of 0 to 16%. Gas exchanges were measured using a portable breath by breath metabolic system (Metamax 3B - Cortex - Leipzig - Deutschland).

Cr per unit of distance was calculated as the net oxygen consumption (V O₂) relative to the body mass per metre (mL.kg^-1.m^-1). For each subject, a mean Cr over two minutes was calculated after the achievement of a steady state in the V O₂ response. A theoretical uphill Cr was calculated using level Cr and di Prampero equation (5).

2.4. Statistical Analysis

Data are expressed as mean ± standard deviation. The correlation coefficient (r) with 95% confidence interval was used to examine the relationships between the selected variables. The relative error between the measured and the theoretical uphill Cr was calculated as follows:

Equation 1.

Statistical analyses were performed using statistica (Statsoft.com, 2011), and the significance level was set at P < 0.05.

3. Results

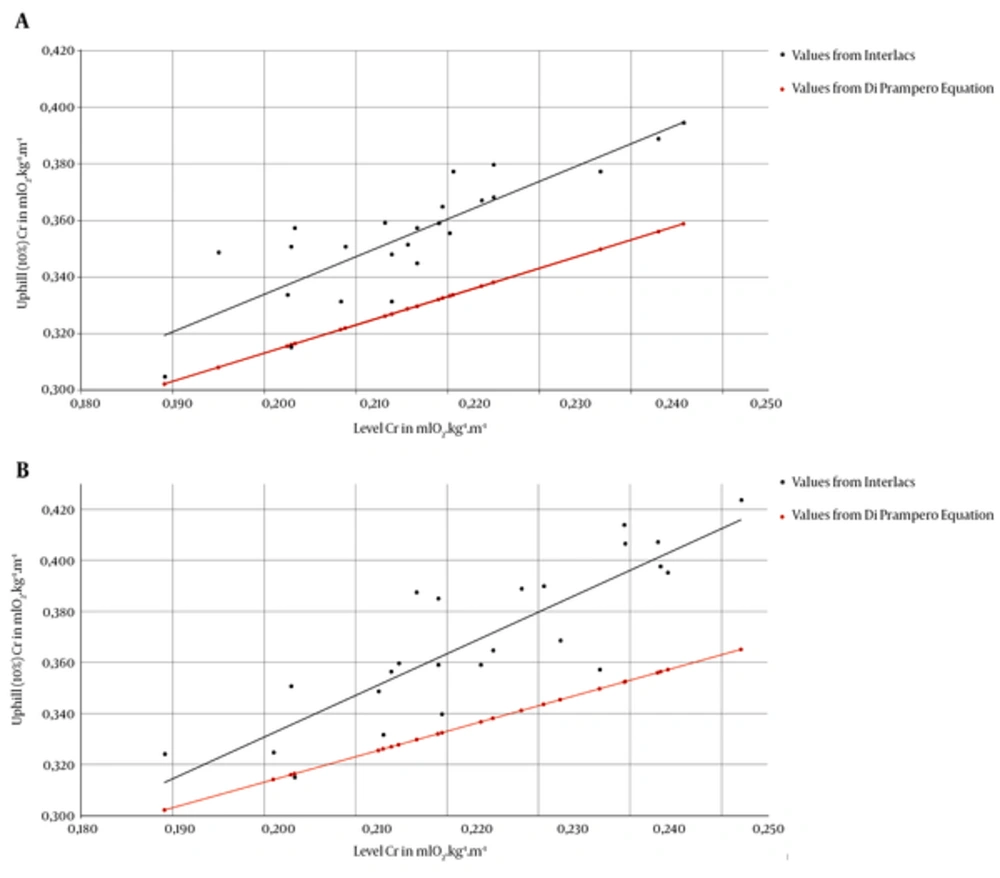
The heterogeneity of the population was attested by a coefficient of variation (CV) of the mean performance on the MUM (728 ± 117 minutes) greater than 15% (CV = 16.1 %). Crs calculated before the MUM: Cr_0% = 0.216 (± 0.014) and Cr_10% = 0.355 (± 0.022) mLO₂.kg^-1.m^-1 (Figure 1A) and after the MUM: Cr_0% = 0.223 (± 0.016) and Cr_10% = 0.369 (± 0.030) mLO₂.kg^-1.m^-1 (Figure 1B) were strongly correlated, with r = 0.84 ± 0.25, P < 0.001, and r = 0.86 ± 0.24, P < 0.001 respectively, (Figure 1A and B). The averaged absolute error between the measured and the theoretical uphill Cr attained 7.9 ± 3.8 % in pre-fatigue and 8.5 ± 4.5 % in post-fatigue.

A and B, Relationship between uphill (10%) and level energy cost of running in a homogeneous group of mountain ultra-endurance runners, and the comparison with di Prampero equation; pre-MUM (A) and post-MUM (B).

Figure 1.

A and B, Relationship between uphill (10%) and level energy cost of running in a homogeneous group of mountain ultra-endurance runners, and the comparison with di Prampero equation; pre-MUM (A) and post-MUM (B).

4. Discussion

On an MUM, as on the road, running velocity sustained over a prolonged time is directly proportional to maximal sustainable V O₂ (Oxygen uptake in L.mn^-1)and inversely proportional to Cr (1). In previous studies, Crs were measured on level running to compare runners. A lack of information exists concerning the values of level and uphill energy cost of mountain runners when running and walking, as well as the significance of the link between these costs. Even if mountain ultra-marathoners could sacrifice Cr in order to minimize lower limb tissue damages (4), performance would remain dependent on running economy, particularly on positive slopes that represent an important part of the total race time. Therefore, the value of uphill Cr should be a relevant factor to evaluate the athletes’ performance capacity. Similarly, the relationship between uphill and level Cr is interesting as part of preparing athletes (Balducci et al., 2016) (6), by developing a runner profile with strengths and weaknesses. For example, a runner with a relatively bad uphill Cr should spend more time training on hilly terrain. As hypothesized, a strong correlation was observed in the heterogeneous group tested in the present study between level and uphill Cr in pre-MUM and post-MUM. This result differs from the results previously reported by Balducci et al. (2016) in a smaller and homogeneous group of runners (6). This indicates that the subject’s morphological, muscular, and technical parameters have an influence on the energy expenditure in running, whatever the slope. However, the relative error between the theoretical and the measured uphill Cr attained 7.9 and 8.5% in the group, in pre-fatigue and post-fatigue respectively and more than 14% in some subjects. The relative error calculated indicates that some subjects are more challenged than others when running uphill. Moreover, the measured Cr_10% are systematically higher than the calculated ones in this study before and after the MUM. This is somewhat surprising considering that the runners are well-accustomed to uphill running. However, some methodological points may explain the differences between di Prampero et al.’s (2009) (5) Crs and those measured in the present study. Indeed, di Prampero et al. calculated the Cr in mLO₂.kg^-1.m^-1 after Minetti et al.’s (2) equation in J.kg^-1.m^-1, assuming that 1 mLO₂ = 20.9 J for a mean respiratory exchange ratio (RER) of 0.96. Actually, RER found in the present study, at 0 and 10% slope in pre-fatigue, were 0.90 and 0.93, respectively. Consequently, Cr values in mLO₂.kg^-1.m^-1 measured in this study are logically slightly greater than those calculated after di Prampero equation. Variance may, also, be explained by differences in the protocols (measuring at a same relative intensity versus a same speed; different sample sizes) and the equipment used to analyze the expired air. Therefore, as proposed by (6), it seems that a single short duration uphill test should be performed in high level runners to measure the athletes’ running energy cost at positive grades in order to evaluate their performance capabilities. Indeed, the stability of the correlations post-fatigue shows that the knowledge of the costs pre-fatigue can be predictive of the performance in the long run.

This study has some limitations; Crs were calculated on a treadmill where gait characteristics may differ from over ground running, which may change the costs. Another study limitation concerns the slope condition applied in the present study; 10% may appear as a steep slope on the treadmill, but in mountain running, slopes may frequently exceed this percentage.

4.1. Conclusion

The results of this study demonstrate that uphill Crs are related to level Crs in a large heterogeneous group of mountain runners, but theoretical uphill Crs are systematically lower than the measured ones, with individual differences ranging from 0% to 14%. Thus, an additional uphill test is still necessary to evaluate the performance parameters in the high level homogeneous mountain endurance runners. A short graded (5 mn at 10 or 12.5%) test should be performed at a submaximal intensity (around 40% of level V O₂ max) to evaluate one runner’s uphill efficiency. The difference between the measured and the theoretical uphill Cr value would allow to assess uphill running efficiency of an athlete and to modify training modalities. For example, a runner presenting a large difference between the calculated and the measured uphill Cr should spend more time running on mountain trails.