Abstract
Background:
Many papers have been published on the topic of basketball players’ performance. Most of them have come from authors covering the field from USA and Europe, whereas the number of papers from the rest of the world, particularly Asia, has so far been small in numbers.Objectives:
Evaluate the significance of the observed parameters in relation to the game outcome (winning/losing) at the last continental championship, 2017 FIBA Asia Cup.Methods:
The sample of entity consisted of 40 games played at 2017 FIBA Asia Cup. The sample of variables consisted of 13 variables registered in the manner as set out by FIBA regulations and 15 derived (relative) variables. Accordingly, two basic models of regression were formed, i.e. absolute and relative, and they had the number of total points scored as their dependent variable. The correlation between the two models was performed by means of regression and correlation analysis of the two models - stepwise regression.Results:
The obtained regression models and partial correlation indicate that winning and losing performance was heavily influenced in the absolute model, by the following: ΔFGM, ΔMFT, and ΔM3, accounting for 95.9% of difference. The second model extracted: ΔFG%, ΔTO%, ΔDR%, ΔPTS3%, and ΔFT%, accounting for 90.7% of difference between winning and losing teams.Conclusions:
Considering the significance of shooting and defensive rebounding, basketball coaches have been strongly advised, in this and many previous works, to pay special attention to these segments of the game.Keywords
Asian Cup Basketball Defensive Rebounds Lose Shooting Stepwise Regression Turnovers Winning
1. Background
Interpretation of basketball tactics, i.e. evaluation of individual, group and team performance in competition -or even more generally speaking- the assessment of tactical performance in team sports, has long been in the focus of sport researchers and coaches alike. Performance analysis is an objective method of performance monitoring in which relevant data can easily be analyzed in a consistent and reliable way, so that information feedback is readily obtained (1). The underlying reason for performance analysis utilization has generally been the fact that it augments our ability to understand sports, which in turn facilitates decision-making for both coaches and players as main actors in sporting events (2). We should take David Smith’s point of view in that respect - the entire issue of performance analysis has certain limitations in the sense that world-best sports performances appear to plateau for only short periods of time before being taken to new levels (3).
Some authors even think that: “In a broader sense, match analysis, namely the study of a competition, has always existed” (4), however Samuel Thornton notes that keeping record of sport performance can be dated back to the 15th century and the first records from structures in dancing movements (5). The first set of objective results of sport performance in team sports were recorded in 1910 when Hugh Fullerton gave his insight into the science of baseball by providing information on the influence of pitching, hitting, and running on the final score (6). Fullerton’s work is therefore considered to be the first scientific research which dealt with sport performances and the influence they had on the final result in a particular sport. Since then, many authors have tackled the same issue by pointing out the importance of proper distinguishing of tactical performances across different team sports.
Basketball has had the reputation and history of a leading sport in terms of notational analysis application (7), and it is also one of the first team sports which “recognizes how important it is to analyze performance indicators because it has been a long time since they are being collected, allowing coaches to rise their knowledge” (8). Johnson highlights that “Basketball in particular has seen a drastic rise in the use of analytics” (9). The first researcher to publish works from this field was Messersmith. He published works in notational analysis about the distance covered by basketball players dating from 1931 to 1944 (10, 11). Many other researchers from this age were inspired by Messersmith’s breakthroughs, for example Elbel and Allen, who introduced the concept of situational analysis by evaluating team and individual performance through subjective recording of game events that might have had a positive or negative influence on the final score (12).
The scientific research of notational analysis can be classified into several subcategories (13, 14): (a) Research on the structure of the game of basketball; (b) evaluation of success in a basketball match, (c) situational efficiency in basketball, and (d) research dealing with anthropological significance of certain types of basketball players and their influence on the final score.
There are almost as many classifications of the structure of basketball as there are authors (15), over 200 different systems of objective evaluation of basketball can be found in the present literature (16). For our purposes, these systems are recognized as having: Simple linear combination, simple linear combination of Z values, partially weighted linear combinations, index of absolute and relative efficiency of the basketball player, MVP evaluation, Swalgin’s evaluation system, and PC system for evaluation of basketball players (17). Martinez even claims that the pursuit of the best performance-related evaluation among basketball players has turned into the Quest for the Holy Grail (16). The reason lies first and foremost in the fact that there is the non-linearity of the relationship between efficiency and multidimensionality, as well as the unpredictability of players’ reactions in concrete, ever-changing conditions of the game (18). In effect, these volatile conditions have urged researchers to come up with novel approaches to the subject matter in order for them to create enhanced systems for selection and development of basketball players, selection of more efficient and reliable training methodologies, and selection of strategic and tactical frameworks, which might result in the desired game outcome (19). This quest is best described by the great NBA coach, Pat Riley, who claimed that not all basketball skills can be measured mechanically, but all of them are still measurable in a way which makes observed and recorded game events transferrable into numerical values (20).
2. Objectives
The objective of the present study is to evaluate the significance of the observed parameters of situational efficiency in relation to the final score of the matches played at 2017 FIBA Asia Cup for men. To determine whether the objective has been reached or not, the study’s findings should explain if the number of points separating the winning from losing team has been in the function of differences of quantitatively observed absolute and relative indicators of the situational analysis in basketball.
3. Methods
3.1. Sample and Variables
The sample of entity in this work consisted of forty (n = 40) games played at the 29th continental championship, 2017 FIBA Asia Cup. The event took place in Lebanon from 8th to 20th August, with participation of 16 national teams which qualified for the championship: Australia, China, New Zealand, Iran, Philippines, Jordan, South Korea, Chinese Taipei, Japan, Qatar, India, Kazakhstan, Lebanon, Hong Kong, Syria, and Iraq.
Data collection during the game needed to be objectified and unified for all observed segments of the match. With respect to that, FIBA standardized 13 indicators of situational efficiency. The sample of variables for this work consisted therefore of manifest variables, which were collected and registered in compliance with FIBA statistics rules and regulations (21): PST - total points, A2 - 2 points attempted, M2 - 2 points made, A3 - 3 points attempted, M3 - 3 points made, AFG - field goals attempted, MFG - field goals made, AFT - free throws, MFT - free throws made, OR - offensive rebounds, DR - defense rebounds, TOTR - total rebounds, AS - assists, PF - personal fouls, TO - turnovers, ST - steals, and BS - block shots.
Alongside variables with absolute values, the present study included the following variables expressed in relative values: 2PTS% - percentage two points (M2/A2) × 100, 3PTS% - percentage three points (M3/A3) × 100, FG% - percentage field goals (MFG/AFG) × 100, FT% - percentage free throws (MFT/AFT) × 100, OR% - efficiency percentage of offensive rebounds in relation to field points missed {OR/(FGA - FGM) + [(FTA - FTM) = 2]} × 100, DR% - efficiency percentage of defense rebounds in relation to field points missed by opponent {DR/(FGAopp - FGMopp) + [(FTAopp - FTMopp) = 2]} × 100, AS% - percentage of assist efficiency (AS/MFG) × 100, PCTPF - percentage of personal foul efficiency (PF/BP)*100, TO% - turnover percentage of inefficiency (TO/BP) × 100, ST% - steals percentage of efficiency (ST/BPopp) × 100; BS% - block percentage of efficiency (BS/ BPopp) × 100, and TBP - team ball possession AFG + 0.5 x FTA - ORB + TO.
Various formulas for calculating relative variables of standardly observed parameters of basketball games can be found in the research literature. The present study adopted the format and recommendations set out by Trninic (22), whereas the variable TBP was calculated according Oliver’s (23) formula, the same approach that had been used by Haruhiko Madarame who compared three FIBA Asia Championships (2011, 2013, and 2015) to FIBA EuroBasket (24). The mentioned research dealt with game-related statistics, which can be readily compared against our findings.
3.2. Statistical Analysis
The difference between the winning and losing team is, as in many team sports, reflected in the diffidence in the total number of points scored at the end of the game. For our purposes, let’s label this difference with ΔPTS. This difference comes as the result of all observed game parameters, or put simply, it is in the function of all parameters. Therefore, ΔPTS can also be defined as an outcome of all observed game parameters as they eventuate. Scoring as many as 80 points does not imply that a team has won, or lost, the game, because the opponent may score only a few points more, or few points less, to put itself in the winning/losing position. Even more specifically, when standard parameters of the game are taken in total, then the difference in the number of total points scored is nothing less than the result of all observed parameters taken together. Bearing this fact in mind, the main assumption about the influence of certain game parameters on the final score is that the difference between the total points scored (ΔPTS) is in function of all other game parameters. For that reason, to design a reliable quantitative model measuring evaluation of influence of certain standard game parameters on the final result, one should make sure the following has been achieved: (a) formation of multiple linear regression models in which ΔPTS stands as a subordinate (dependent) variable, while differences (Δ) of other game parameters stand as insubordinate (independent) variables; and (b) selection of variables in the set of regression should point to the specific weight of each observed variable (25).
When basketball games are observed, researchers are able to record multiple standard and derived parameters, and by processing them we can get an insight into the nature of indicators which may determine the final outcome of the game result-wise. This study made use of two basic models of regression. Both of them incorporated the same dependent variable, ΔPTS. The first model was designed to have a set of independent variables, i.e. to be comprised of differentiations between all absolute parameters of the observed parameters of the game:
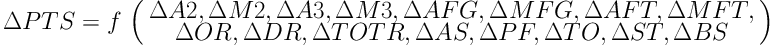
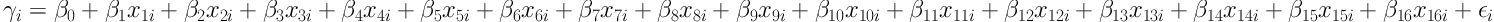
with variables labeled in the equation as: x1i = ∆A2, x2i = ∆M2, x3i = ∆A3, x4i = ∆M3, x5i = ∆AFG, x6i = ∆MFG, x7i = ∆AFT, x8i = ∆MFT, x9i = ∆OR, x10i = ∆DR, x11i = ∆TOTR, x12i = ∆AS, x13i = ∆PF, x14i = ∆TO, x15i = ∆ST, and x16i = ∆BS.
The second model was designed to have all independent variables of relative (derived) parameters of the game:
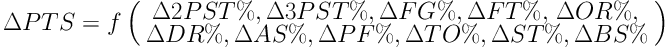
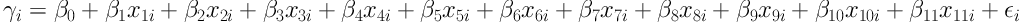
with variables labeled in the equation as: x1i = ∆PTS2%, x2i = ∆PTS3%, x3i = ∆FG%, x4i = ∆FT%, x5i = ∆OR%, x6i = ∆DR%, x7i = ∆AS%, x8i = ∆FT%, x9i = ∆TO%, x10i = ∆ST%, and x11i = ∆BS%.
Both models have PTS (points total scored) as the dependent variable - which is rather logical if we set scoring more points than your opponent as the main objective of the competing basketball teams.
Data processing between and within the variables was performed by means of adequate statistical procedures of regression and correlation analysis applied to the established regression models, and it was based on gradual regression (stepwise), with the defined conditions of regression in place, regarding inclusion or omission of variables in/from the model, i.e. F criterion for inclusion of variable into the equation set at 0.05 level of significance, and 0.10 for omission from the equation (standard values). Standardization at this level ensured consistency and comparability of results at different levels and in different time periods. Also, the determined variables and their parameters were examined in terms of the level of significance they exhibited (t-test and F test), all with an aim to obtain well-defined models providing ground for valid extrapolation.
4. Results
Tables 1 and 2 show the results of regression and correlation analysis of models one and two, relating to the observed parameters in basketball matches.
Regression and Correlation Analysis of the First Model at the 2017 FIBA Asia Cupa
| Model | SE | t | P | r |
|---|---|---|---|---|
| Constant | 0.74 | 1.39 | 0.17 | - |
| ΔMFG | 0.71 | 27.57 | 0.00 | 0.98 |
| ΔMFT | 0.74 | 12.06 | 0.00 | 0.90 |
| ΔM3 | 0.12 | 8.16 | 0.00 | 0.81 |
Regression and Correlation Analysis of the Second Model at the 2017 FIBA Asia Cupa
| Model | SE | t | P | r |
|---|---|---|---|---|
| Constant | 0.23 | 0.17 | 0.86 | |
| ΔFG% | 0.09 | 10.67 | 0.00 | 0.88 |
| ΔTO% | 0.11 | -8.41 | 0.00 | -0.82 |
| ΔDR% | 0.06 | 7.88 | 0.00 | 0.80 |
| ΔPTS3% | 0.07 | 4.01 | 0.00 | 0.57 |
| ΔFT% | 0.04 | 2.64 | 0.01 | 0.41 |
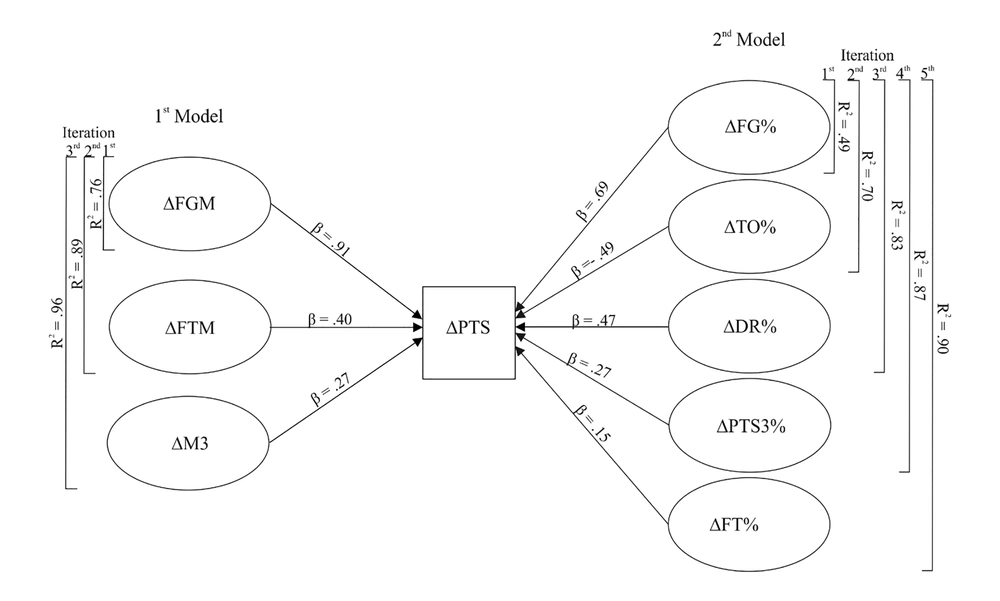
From the obtained regression models and based on the quotients of partial correlation, it can be concluded that, in the first model, the final score of games played at 29th FIBA Asia Cup 2017 was influenced by the variables ΔFGM - field goals made (β = 0.91, P < 0.00) with partial correlation rp = 0.98, and ΔMFT - free throws made (β = 0.40, P < 0.00) with partial correlation rp = 0.90, and ΔM3 - 3 points made (β = 0.27, P < 0.00) with partial correlation rp = 0.81. The second models recorded the following variables: ΔFG% - percentage field goals (β = 0.67, P < 0.00) with partial correlation rp = 0.88, ΔTO% - turnover percentage of inefficiency (β = -0.49, P < 0.00) with partial correlation rp = -0.82, ΔDR% - efficiency percentage of defense rebounds in relation to field points missed by opponent (β = 0.47, P < 0.00) with partial correlation rp = 0.80, ΔPTS3% - percentage three points (β = 0.27, P < 0.00) with partial correlation rp = 0.57, and ΔFT% - percentage free throw (β = 0.15, P < 0.00) with partial correlation rp = 0.41.
Data analysis is particularly noteworthy when looked at from the aspect of partial correlation (rp), due to significant influence that certain selected variables have on the final score of the game (with other, unselected, variables remaining unchanged).
Based on what can be seen from Tables 3 and 4, it can be inferred that the regression models have statistical significance relative to the included variables.
ANOVA of the First Model at the 2017 FIBA Asia Cup
| Model | Total | df | s | F | P |
|---|---|---|---|---|---|
| Regression | 7580.67 | 3 | 2526.89 | 306.36 | 0.00 |
| Residual | 296.94 | 36 | 8.248 | ||
| Total | 7877.60 | 39 |
ANOVA of the Second Model at the 2017 FIBA Asia Cup
| Model | Total | df | s | F | P |
|---|---|---|---|---|---|
| Regression | 7117.55 | 5 | 1423.51 | 63.68 | 0.00 |
| Residual | 760.05 | 34 | 22.35 | ||
| Total | 7877.60 | 39 |
More specifically, both models exhibit significant correlation between dependent (subordinate) variable of (ΔPTS), and the set of insubordinate variables included in the model. The variables included in the first model, which was based on absolute variables and obtained after 3rd iteration, explain 95.9% of the phenomenon (R2 = 0.96, F (3.36) = 306.36, P < 0.00). The variables included in the second model, based on relative variables derived from the absolute ones, explain 88.9% of the phenomenon (R2 = 0.90, F (5.34) = 63.68, P < 0.00).
Figure 1 shows the included variables from the first and second model with iterations performed, i.e. values of adjusted R square in each performed iteration.
Obtained variables in the first and second model with iteration steps. ΔPTS, difference in the number of total points scored; ΔFGM, difference in field goals made; ΔFTM, difference in free throws made; ΔM3, difference in 3 points made; ΔFG%, difference in percentage field goals; ΔTO%, difference in turnover percentage of inefficiency; ΔDR%, difference in efficiency percentage of defense rebounds in relation to field points missed by opponent; ΔPTS3%, difference in percentage three points; ΔFT%, difference in percentage free points; model 1, ΔPTS = f (ΔA2, ΔM2, ΔA3, ΔM3, ΔAFG, ΔAFT, ΔMFT, ΔOR, ΔDR, ΔTOTR, ΔAS, ΔPF, ΔTO, ΔST, ΔBS); model 2, ΔPTS = f (Δ2PTS%, ΔPTS3%, ΔFG%, ΔFT%, ΔOR%, ΔDR%, ΔAS%, ΔPF%, ΔTO%, ΔST%, ΔBS%); R2, adjusted R square stepwise regression; β, standardized coefficient beta.
The values of adjusted R square in the first model (the final step of iteration include) are: (1st) R2 = 0.76, F (1.38) = 127.24, P < 0.00; and, (2nd) R2 = 0.89, F (2.37) = 153.67, P < 0.00. Whereas the second model has the following values for adjusted R square: (1st) R2 = 0.49, F (1.38) = 38.27, P < 0.00; (2nd) R2 = 0.70, F (2.37) = 45.84, P < 0.00; (3rd) R2 = 0.83, F (3.36) = 64.64, P < 0.00; and, (4th) R2 = 0.87, F (4.35) = 66.47, P < 0.00. This provides conclusive evidence that both models show significant correlation between the dependent variable PTS, or ΔPTS, and the relating sets of independent variables.
5. Discussion
Sports analytics, data collection and analysis, when coupled with mathematical and statistical models of data interpreting, can contribute to an improved performance development among both individual players and teams during basketball games (26). Therefore, in-game statistics has become the subject of interest of both basketball coaches and scientific researchers (27); most of the research papers quoted in the present work have dealt with basketball games using quantitative analysis as the basis for describing and understanding individual and team performance during basketball matches (28). Data collected and analyzed accordingly, may be used in different ways - but in recent years they have mostly been used to discriminate between the winning and losing teams (29). Following the suit, the present study aimed to make an analysis relating to which variables, during 29th FIBA Asia Cup, discriminated between the winning and losing teams.
This continental championship was held according to a specific combined tournament format and did not have issues as some researchers had in their works, like home-court advantage or in-form and out-of-form team performances during season long competitions, or as some authors described this phenomenon: “Discriminate between season-long successful and unsuccessful basketball teams” (27) in season-long national championships. Due to the relatively small number of games played during this continental championship, we didn’t make different game subgroups as the differences between the winning and losing teams, in that respect, were not evident in terms of the standard indicators of basketball efficiency. Here we have followed cluster analysis guidelines of Jaime Sampaio and Manuel Janeira, who defined three types of basketball matches for subsequent analysis based on final score differential: close games (games with undecided results up until the very last seconds of the game played), balanced games (games with relatively low final score differential), and unbalanced games (games with relatively high final score differential) (30), because the games played at this continental championship tended to discriminate following the same outline. Future research should focus on the differences between winning/losing teams in a round robin system relative to differences between winning/losing teams in single-elimination system (final stage of championship), as was done by some authors who compared regular season matches to play-off matches (30).
In both observed models, variables included in the first step of iteration were the variables related to field goals: In the first model, the included variable was field goals made (R2 = 0.76, F(1, 38) = 127.24, P < 0.00), explaining 76% of difference between the winning and the losing team at 2017 FIBA Asia Cup, while the second model had the variable of percentage field goals (R2 = 0.49, F(1, 38) = 38.27, P < 0.00) explaining 49% of the difference. To have the variables related to field goals made and field goals attempted as the ones which explain most of the observed phenomenon, is consistent with logic in which the dependent variable of total points scored discriminates the winning from the losing team. Many other researches have come to the same conclusion, i.e. percentage of field goals is the variable with the most significant influence on the discrimination between the winning and losing team (25, 27, 31-35). After all, shooting is one of the most important skills in basketball players. Even if a player has an improved arsenal of other basketball skills, including passing, dribbling, rebounding and defense, which may help him to have high field goals percentage, he will still need to have sufficient shooting skills to score points (23, 36), or as Bill Sharman, one of the four people who was inducted into Naismith Memorial Basketball Hall of Fame both as player and coach, put it: “He wins who scores more points than his opponents in basketball, and shooting is the backbone of the game” (37).
It comes as pretty much coherent with everything said so far that out of eight variables included in this work, six of them (75%) relate to the shooting efficiency, 100% in the first model and 60% in the second model, respectively. Alongside with the variables filed goals made and percentage field goals, free throws made and 3 points made were found significant in the first model (absolute values), and the same for the second model (relative values) - percentage 3 points and percentage free throws. The same findings can be retrieved from many other works - free throws and their efficiency (28, 30, 38-40), and efficiency of 3 point shots (33, 41, 42).
Some previous works (analyzing data from 13th, 14th and 15th World Championship), which applied the same researching methodology as the present study, found the shot-related variables to be dominant in both models (25). The models developed for those championships had nine included variables which were significant in discriminating the winning from the losing team - six out of nine relate to the shooting parameters (66.67%) at the World Championship in Greece, five out of nine (55.56%) at the World Championship in USA, and seven out of nine (77.78%) are shooting variables which were found significant at the World Championship in Japan. It is noteworthy that all the three abovementioned basketball championship reported ΔM2 (2 points made) as the dominant variable with a significant influence on the final score of the game, the same was observed in other researches as well (30, 31, 33, 41, 43), whereas such an outcome was not included as a separate variable; although it was indirectly included as the part of variable field goals made and percentage field goals (presented in this study as sum of ΔM2 + ΔM3). The Asian continental championships held in 2011, 2013 and 2015 recorded a high correlation between 2 points made and the winning teams but only in unbalanced games (24). What might be the underlying cause for this? Many things could account for it: Conceptual and strategic frameworks that participating teams chose to follow, tactical shifts towards certain playing styles, number of players capable of making 3 point shots, tall players capable of taking behind the three-point line shots, etc. Note also that some authors found that in games with winning margin less than 10 points, the winning teams had better 2 point shot percentage, whereas in games with margins of 10+ points, the most significant influence on the final score was recorded in defensive rebounds and assist passes (43). At FIBA Asia Cup 2017, 62.50% of games had final score with 10+ points difference, which points, on the one hand, to uneven balance in quality of the participating teams and, on the other hand, it also indicates that the lack of ΔM2 can be explained by the apparent difference in the quality of the participating national teams.
The similar work whose focus was on the two models from EuroBasket 2011 included thirteen variables, out of which nine, or 75%, were shooting efficiency indicators (44). Therefore, one of the conclusions here is that if teams were to win a basketball game, they should aim at creating plenty of shooting opportunities for their players - a notion observed by other researchers as well (45).
Other studies of the influence of certain game elements on situational efficiency have also found that shooting efficiency and defensive rebounding significantly influence dominant variables in terms of determining the final score of the game (27, 35, 38). Gomez at al. found defensive rebounding as a separate factor which made difference between winning and losing (31), Garcia et al. highlighted the efficiency of 2-point and 3-point shooting with defensive rebounding and assist passes, during the regular season matches, whereas only defensive rebounding had a discriminating influence on the winning/losing team difference in play-offs (43), and de Carvalho et al. found that the game winning was dependent on defensive rebounding, assists, turnovers and 2-point and 3-point shooting efficiency (42). Bartholomew and Collier claim that: “... basketball defensive players and teams are evaluated on traditional basketball metrics such as blocked shots, defensive rebounds, steals, forced turnovers, fouls, and the opponent’s total points and field goal shooting percentage” (46, 47), whereas Trninic et al. assert that: “...defensive rebounds to be not only an indicator of the closing defensive actions, but also as an indicator of overall defensive success; since it follows the unsuccessful opponent’s shot which is, most often, a consequence of the organized pressure defense well performed” (48). Basketball teams with efficient defensive rebounding get more opportunities for shooting, thus creating more scoring chances and potentially win matches (30). Here we have to clarify that it is not just the number of defensive rebounds that can be taken as a reliable indicator, but the efficiency of defensive rebounding as such - something that was pointed out as early as in 1982 by one of the greatest coaches of all times, Dean Smith, in his book titled “Basketball, multiple offense and defense” (49). His research also showed that the winning teams had on average more defensive rebounds, M = 28.20 (0.74), when compared with the losing teams, M = 22.60 (0.86), but also they had more rebounding opportunities on average (3.65). It is only when we take the relative indicators of defensive rebounding that we get a complete picture with respect to the winning teams and their defensive rebounding, i.e. the winning teams managed to get possession of 70% of the shots missed by their opponents, M = 69.64 (1.28), whereas the losing teams got 60% of the missed shots from their opponents, M = 60.65 (1.45).
Madarame found the link between defensive rebounds and winning the matches in both balanced and unbalanced games at three Asian Basketball Championships preceding the 2017 FIBA Asia Cup (24). The situational efficiency variable of defensive rebounding was therefore, alongside with assist passes, found in all the matches played at the championships.
Kubatko et al. proposed, based on their research findings, the inclusion of the four factors into offensive and defensive efficiency analysis, by the following order: Field goal efficiency, offensive rebound percentage, steals and free throws (50). The importance of turnovers relative to the winning/losing outcome of the game was stressed by many researchers (41, 42). For example, a study conducted by Nakic found correlation between the losing teams and personal fouls, turnovers, and missed 2- and 3-point shots (51). This segment of the game was also examined by Fylaktakidou et al., and they found that the underlying reasons for turnovers were the following: passing errors 40.00%, fault ball handling 23.90% and travelling 23.60% (52). Our research found, in the second model, that ΔTO had a significant influence on the final score and that, together with ΔFG%, explained 66% of the research phenomenon (R2 = 0.76, F(3, 36) = 62.54, P < 0.00). This is in line with previous research findings about the defensive rebounding. The winning teams were found to have less turnovers, M = 13.88 (0.53), in comparison to the losing teams, M = 16.50 (0.74). The losing teams had even 1.75 attacks more than the winning teams, or in other terms, they had more of a chance to make more turnovers. It is only with the absolute indicators that we get the clear picture about the whole issue, i.e. relative to the number of offenses, the losing teams made 3.4% turnovers more than the winning teams.
The limitations of this study are primarily concerned with the nature of the study as with regards to the validity and reliability of research findings. For instance, Hughes et al. analyzed different studies (n = 72) from the field of notational analysis and found that almost 70% of authors conducted no examination about the reliability of performance and efficiency indicators (53). Likewise, we should bear in mind that the study data are often provided by data collectors who may not have ample experience in the field, resulting in serious consequences on the reliability of the entire study (54). On the other hand, even coaches are known to be able to observe only around 30% of the events taking place in the course of a basketball match (55). Therefore, we need a reliable and objective set of tools for evaluation of individual and team performances - one example could be the performance analysis (56), a notational approach, which requires an on-going development in terms of its methodological compatibility and overall reliability.
Ibanez et al. pointed out that there are too many studies focusing on game variables differentiating between the winning and losing team but only during a season or two, or during international competitions at best, whereas seldom is the case when researchers examine a set of different basketball seasons for this purpose (27), not to mention a relatively small number of studies examining two or more international competitions (continental championships or cups). Any further research should go in that particular direction (examination of data from consecutive Asian Championships/Cups), and it should be carried out in the similar format with the inclusion of additional game parameters.
5.1. Conclusions
The present study applied the gradual regression models on the eight variables that were found to have the most significant influence on the final score, i.e. those that made most of the difference between the winning and losing teams at 2017 FIBA Asia Cup. Most of the included variables were related to indicators of field goals made, free throws and percentage of points made. Also, the included variables were those relating to defensive rebounding and turnovers. The results obtained in this study are in accordance with many other studies - overall shooting efficiency, particularly field goal efficiency, and defensive rebounds were found to be the main parameters of the situational efficiency with significant influence on the final score in basketball. The obtained results may have a practical value in terms of providing guidelines for basketball coaches in their efforts to maximize the benefits during preparation of their teams for the competitions and regular seasons.
References
-
1.
Hughes MD, Bartlett RM. What is performance analysis? In: Hughes M, Franks I, editors. The essentials of performance analysis: An introduction. London: Routledge; 2008. p. 8-21.
-
2.
O'Donoghue PG. Research methods in performance analysis of sport. London: Routledge; 2010.
-
3.
Smith DJ. A framework for understanding the training process leading to elite performance. Sports Med. 2103;33(15):1103-26. [PubMed ID: 14719980]. https://doi.org/10.2165/00007256-200333150-00003.
-
4.
Ruscello B. Match analysis in team sports [dissertation]. Rome: "Tor Vergata" University of Rome; 2009.
-
5.
Thornton S. A movement perspective of Rudolf Laban. London: Macdonald and Evans; 1971.
-
6.
Fullerton HS. The inside game: The science of baseball. Am Mag. 1912;70:3-13.
-
7.
Mikolajec K, Maszczyk A, Zajac T. Game indicators determining sports performance in the NBA. J Hum Kinet. 2013;37(1):145-51. https://doi.org/10.2478/hukin-2013-0035.
-
8.
Parejo I, Garcia A, Antunez A, Ibanez S. Differences in performance indicators among winners and losers of group a of the spanish basketball amateur league (EBA). J Sport Psychol. 2013;22(1):257–61.
-
9.
Johnson B. Analytics and free throw shooting: Perception vs. reality [dissertation]. Fairfax, VA: George Mason University; 2017.
-
10.
Fay PJ, Messersmith LL. The effect of rule changes upon the distance traversed by basketball players. Res Q Am Assoc Health Phys Educ. 1938;9(2):136-7.
-
11.
Messersmith LL. A study of the distance traveled by basketball players. Res Q Am Assoc Health Phys Educ Recreation. 1944;15(1):29-37.
-
12.
Elbel ER, Allen FC. Evaluating team and individual performance in basketball. Res Q Am Assoc Health Phys Educ Recreation. 1941;12(3):538-55.
-
13.
Jelaska I. Design and application of a new model for evaluating performance in complex sports activities [dissertation]. Split, Croatian: University of Split; 2011.
-
14.
Perica A. Analysis and evaluation of the situation of position and transition defense in the basketball game [dissertation]. Zagreb, Croatian: University of Zagreb; 2011.
-
15.
Selmanovic A. Comparison of the attack structure in European and American basketball [dissertation]. Zagreb: University of Zagreb; 2016.
-
16.
Martinez JA. Factors determining production (FDP) in basketball. Econ Bus Lett. 2012;1(1):21. https://doi.org/10.17811/ebl.1.1.2012.21-29.
-
17.
Dizdar D. Evaluation expensive method to assess the actual quality of basketball [dissertation]. Zagreb, Croatian: University of Zagreb; 2002.
-
18.
Grehaigne JF, Godbout P. Tactical knowledge in team sports from a constructivist and cognitivist perspective. Quest. 1995;47(4):490-505. https://doi.org/10.1080/00336297.1995.10484171.
-
19.
Trninic S, Dizdar D, Dezman B. Empirical verification of the weighted system of criteria for the elite basketball players quality evaluation. Collegium Antropologicum. 2000;24(2):443-65.
-
20.
Riley P. The winner within: A life plan for team players. New York: Putnam's Sons; 1993.
-
21.
2017 FIBA Asia Cup. Mies: International Basketball Federation. 2017, [cited Feb 28]. Available from: http://www.archive.fiba.com/pages/eng/fa/event/p/sid/8110/_/2017_FIBA_Asia_Cup/index.html.
-
22.
Trninic S. Analysis and learning of basketball game. Pula, Croatia: Vikta; 1996.
-
23.
Oliver D. Basketball on paper: Rules and tools for performance analysis. Washington, DC: Brassey’s, Inc; 2004.
-
24.
Madarame H. Game-related statistics which discriminate between winning and losing teams in Asian and European men’s basketball championships. Asian J Sports Med. 2017;8(2). https://doi.org/10.5812/asjsm.42727.
-
25.
Simovic S, Komic J. Analysis of influence of certain elements of basketball game on final result based on differetiant at the XIII, XIV and XV World Championship. Acta Kinesiologica. 2008;2(2):57-65.
-
26.
Drazan JF, Loya AK, Horne BD, Eglash R. From sports to science: Using basketball analytics to broaden the appeal of math and science among youth. MIT Sloan Sports Analytics Conference. Hynes Convention Center, Boston, MA. 2017.
-
27.
Ibanez SJ, Sampaio J, Feu S, Lorenzo A, Gomez MA, Ortega E. Basketball game-related statistics that discriminate between teams’ season-long success. Eur J Sport Sci. 2008;8(6):369-72. https://doi.org/10.1080/17461390802261470.
-
28.
Sampaio J, Janeira M, Ibanez S, Lorenzo A. Discriminant analysis of game-related statistics between basketball guards, forwards and centres in three professional leagues. Eur J Sport Sci. 2006;6(3):173-8. https://doi.org/10.1080/17461390600676200.
-
29.
Williams G. Game-related statistics that discriminate between winning and losing teams in the National Basketball Association [dissertation]. Cardiff: Cardiff Metropolitan University; 2014.
-
30.
Sampaio J, Janeira M. Statistical analyses of basketball team performance: Understanding teams’ wins and losses according to a different index of ball possessions. Int J Perform Anal Sport. 2017;3(1):40-9. https://doi.org/10.1080/24748668.2003.11868273.
-
31.
Gomez MA, Lorenzo A, Barakat R, Ortega E, Palao JM. Differences in game-related statistics of basketball performance by game location for men's winning and losing teams. Percept Mot Skills. 2008;106(1):43-50. [PubMed ID: 18459354]. https://doi.org/10.2466/pms.106.1.43-50.
-
32.
Csataljay G, James N, Hughes M, Dancs H. Performance differences between winning and losing basketball teams during close, balanced and unbalanced quarters. J Hum Sport Exercise. 2012;7(2):356-64. https://doi.org/10.4100/jhse.2012.72.02.
-
33.
Ibanez SJ, Garcia J, Feu S, Lorenzo A, Sampaio J. Effects of consecutive basketball games on the game-related statistics that discriminate winner and losing teams. J Sports Sci Med. 2009;8(3):458-62. [PubMed ID: 24150011]. [PubMed Central ID: PMC3763293].
-
34.
Leicht AS, Gomez MA, Woods CT. Explaining match outcome during the Men's basketball tournament at the Olympic games. J Sci Med Sport. 1968;16(4):468-73. [PubMed ID: 29238245]. [PubMed Central ID: PMC5721175].
-
35.
Simovic S, Nicin D. Latent structure of efficiency at 2009 continental (zone) basketball championships. Res Kinesiol. 2011;39(1).
-
36.
Piette J, Anand S, Zhang K. Scoring and Shooting Abilities of NBA Players. J Quant Anal Sports. 2010;6(1). https://doi.org/10.2202/1559-0410.1194.
-
37.
Hoover P. Pro shooting secrets. 2nd ed. Columbus, OH; 2012.
-
38.
Csataljay G, O’Donoghue P, Hughes M, Dancs H. Performance indicators that distinguish winning and losing teams in basketball. Int J Perform Anal Sport. 2017;9(1):60-6. https://doi.org/10.1080/24748668.2009.11868464.
-
39.
Reano GMA, Calvo LA, Toro OE, editors. Differences between winning and losing under-16 male basketball teams. World Congress of Performance Analysis of Sport VII–Proceedings. 2006. 2006. p. 142-9.
-
40.
Tavares F, Gomes N. The offensive process in basketball – a study in high performance junior teams. Int J Perform Anal Sport. 2003;3(1):34-9. https://doi.org/10.1080/24748668.2003.11868272.
-
41.
Lorenzo A, Gomez MA, Ortega E, Ibanez SJ, Sampaio J. Game related statistics which discriminate between winning and losing under-16 male basketball games. J Sports Sci Med. 2010;9(4):664-8. [PubMed ID: 24149794]. [PubMed Central ID: PMC3761811].
-
42.
de Carvalho EMO, Leicht AS, Nakamura FY, Okuno NM, Alves Okazaki VH. Team statistical determinants of victory in Brazilian basketball. MOJ Sports Med. 2017;1(4):1-7. https://doi.org/10.15406/mojsm.2017.01.00018.
-
43.
Garcia J, Ibanez JS, Gomez AM, Sampaio J. Basketball game-related statistics discriminating ACB league teams according to game location, game outcome and final score differences. Int J Perform Anal Sport. 2013;14(2):443-52. https://doi.org/10.1080/24748668.2014.11868733.
-
44.
Simovic S, Komic J, Matkovic B, Nicin D. Analysis of results at Eurobasket 2011 – final results of observed elements of basketball game. 3rd International Scientific Conference Anthropological Aspects of Sports, Physical Education and Recreation. Faculty of Physical Education and Sport, University of Banja Luka, Banja Luka. 2012. p. 19-28.
-
45.
Sampaio J, Lago C, Drinkwater EJ. Explanations for the United States of America's dominance in basketball at the Beijing Olympic Games (2008). J Sports Sci. 2010;28(2):147-52. https://doi.org/10.1080/02640410903380486.
-
46.
Bartholomew JT, Collier DA. A defensive basketball efficiency score using data envelopment analysis. J Sport Manag Res. 2011.
-
47.
Bartholomew JT, Florida G, Collier DA. The role of contested and uncontested passes in evaluating defensive basketball efficiency. J Serv Sci. 2011;4(2):33-42. https://doi.org/10.19030/jss.v4i2.6643.
-
48.
Trninic S, Dizdar D, Luksic E. Differences between winning and defeated top quality basketball teams in final tournaments of European club championship. Collegium antropologicum. 2002;26(2):521-31.
-
49.
Smith D. Basketball, multiple offense and defense. 4th ed. Boston, MA: Allyn and Bacon; 1999.
-
50.
Kubatko J, Oliver D, Pelton K, Rosenbaum DT. A starting point for analyzing basketball statistics. J Quant Anal Sports. 2007;3(3). https://doi.org/10.2202/1559-0410.1070.
-
51.
Nakic J. Differences in standard and derived situation efficacy parameters between men's and women's basketball teams in senior European basketball championships in 2003 [dissertation]. Zagreb: University of Zagreb; 2004.
-
52.
Fylaktakidou A, Tsamourtzis E, Zaggelidis G. The turnovers analysis to the women's national league basketball games. Sport Sci Rev. 2011;20(3-4):69-83. https://doi.org/10.2478/v10237-011-0055-2.
-
53.
Hughes M, Cooper SM, Nevill A. Analysis procedures for non-parametric data from performance analysis. Int J Perform Anal Sport. 2002;2(1):6-20. https://doi.org/10.1080/24748668.2002.11868257.
-
54.
Skegro D. Evaluating different types of attack in a basketball game based on their start, outcome, duration and number of additions [dissertation]. Zagreb, Croatian: University of Zagreb; 2013.
-
55.
Franks I, Miller G. Eyewitness testimony in sport. J Sport Behav. 1986;9:39-45.
-
56.
Hughes M, Franks I. The essentials of performance analysis: An introduction. Routledge; 2007.