Abstract
Background:
Adsorption isotherms describe the relationship between the equilibrium concentration of the adsorbed matter in the solution and the amount of adsorbed matter on the surface of the adsorbent.Objectives:
The main objective of the present research was to investigate different adsorption isotherms for describing adsorption of humic acid by nanoclay.Methods:
In this study, Langmuir, Freundlich, BET, Temkin and Dubinin Radushkevich isotherms, for describing the behavior of humic acid adsorption by bentonite and montmorillonite nanoparticles, were examined.Results:
The results showed that due to the regression coefficient (R2), humic acid adsorption on bentonite and montmorillonite nanoparticles has greater compliance with Dubinin Radushkevich isotherms. The value of E or average energy of adsorption for humic acid by bentonite and montmorillonite nanoparticles was 0.17 and 0.15 kJ mol-1, respectively, which specifies that the type of adsorption of humic acid on both nanoparticles was physisorption. The qmax value obtained from the Dubinin-Radushkevich isotherms, for bentonite and montmorillonite nanoparticles were 27.78 and 28.70 mg/g, respectively.Conclusions:
According to the results of this study, bentonite and montmorillonite nanoparticles have a great potential for the removal of humic acid from aqueous solutions.Keywords
Nanoparticles Bentonite Montmorillonite Isotherms Humic Acid
1. Background
Humic substances are natural organic polyelectrolyte materials that form most of the dissolved organic carbon in aquatic environments (1). Humic substances are known as precursors of disinfection byproducts (2, 3). The most common disinfection byproducts with chlorine compounds include thrihalomethnes and halo acetic acids, which are toxic, cancer-causing and mutagenic. Humic acid and fulvic are precursors of thrihalomethnes. Thrihalomethnes are organic halides and include: chloroform, bromo-dichloromethane, dichloro-bromo methane and bromoform (4, 5). The existence of humic acid on the surface of water causes many problems such as taste and odor, color, lower efficiency of treatment processes, reaction with chlorine and production of disinfection byproducts (6). Thrihalomethnes causes many cancers, some of these cancers are bladder cancer, kidney cancer, colon and small bowel cancer (7).
Among the various processes for removal of humic acid, the adsorption process, because of its high potential for removal of small molecules including organic material, seems to be one of the best solutions for wastewater treatment (8).
Nanoparticles as adsorbents have two important features that make them suitable as absorbents. First, they have significantly wider surface areas than other particles. Furthermore, they can be combined with different chemical groups to increase their tendency to remove the target compounds (9, 10).
In the recent years, many studies have been conducted on the use of clay to remove various contaminants from the environment, yet the number of investigations on the use of nano clay is very limited. Clay is one of the low cost nano materials, which has properties such as being non-toxic and environmentally friendly, having high specific surface area and high adsorption capacity (11).
The amount of adsorbate that an adsorbent could adsorb is a function of the characteristics of the adsorbate, adsorbent and type of adsorption reaction. During the adsorption process, some of the adsorbate from the liquid phase tends to go to the solid phase and vice versa, and after a certain reaction time, a dynamic equalization between the adsorbate on the surface of adsorbent and its final form in the solution phase, will be established. When an adsorbent, adsorbate and solution achieve a minimum free energy, the thermodynamic equalization of the system will occur. Generally, the amount of the adsorbate per unit of adsorbent dosage is expressed as a function of the equilibrium concentration in the solution phase and at constant temperature; and regarding introduction at a fixed temperature, they are called adsorption isotherm (12). Models and equations of the equilibrium of adsorption isotherms are used to describe adsorbent surface properties, providing a view of the adsorption process and describing the experimental data. Isotherms are also an important factor in designing adsorption systems and they describe the relationship between the concentration of the adsorbate and adsorption capacity of the adsorbent. Adsorption isotherms for different systems can take several different forms.
2. Objectives
In this study, we examined the data of the equilibrium process of humic acid adsorption by bentonite and montmorillonite nanoparticles. We also studied the compatibility of the adsorption process of humic acid with these isotherms: Langmuir, Freundlich, BET, Temkin and Dubinin Radushkevich.
3. Methods
This investigation was a practical experimental study that was performed in a batch system. Adsorbents used in this study were nanoclay (bentonite and montmorillonite nanoparticles). Bentonite and montmorillonite nanoparticles were bought from the Nano Sany corporation. These nanomaterials were washed and dried for 24 hours and were used for adsorption experiments. HCl and NaOH were used to adjust the pH. Stock solution of humic acid was prepared by solving certain amounts of humic acid sodium salt (made by Acros Company) in distilled water. The concentration of stock solution was 500 mg/L.
In order to determine the isotherms, the dosage of nano adsorbents was 100 mg and the volume of humic acid solution was 100 mL, while there were different initial humic acid concentrations (10, 15, 20, 30 and 40 mg/L). Experiments were carried out at a temperature of 25°C. After the reaction, the samples were filtered and then were read with a spectrophotometer (+UV/VIS spectrometer T80) at a wavelength of 254 nm. The amount of humic acid adsorption capacity by bentonite and montmorillonite nanoparticles was calculated with Equation 1:
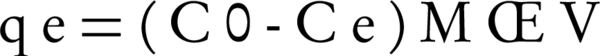
Where, C0 and Ce are the initial and final concentrations of humic acid (mg/L), respectively. M is adsorbent dosage (g), and V is the volume of the solution in liters.
In this study, we examined the Freundlich, Langmuir BET, Temkin and Dubinin-Radushkevich adsorption isotherms for mathematical modeling of adsorption of humic acid.
Langmuir isotherm is based on the monolayer and uniform (homogenous) adsorption of material with the same energy on the entire surface of the adsorbent. Unlike Langmuir model, Freundlich isotherm is based on the heterogeneous adsorption of humic acid by the adsorbent.
3.1. Freundlich Isotherm Model
Freundlich equation describes the adsorption process at a heterogeneous level (according to the adsorption energy). In fact, the Freundlich model assumes that the adsorption process occurs in a mono-layer but is not uniform and homogenous. Equation 2 represents the mathematical model of Freundlich isotherm (13, 14).
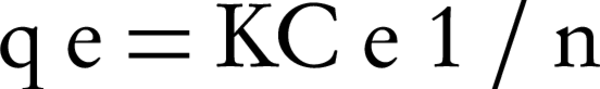
Where, qe is the mass ratio of the solid phase, which is the ratio of the adsorbed mass to the mass of adsorbent (mg /g), Ce is the equilibrium concentration (mg/L) and K is the experimental constant (Freundlich equation coefficients).
3.2. Langmuir Isotherm Model
In the adsorption isotherm of Langmuir, adsorption is single layered and the adsorption regions on the surface of the adsorbent are uniform with the same adsorption power. Connections and bonds of adsorption process are also reversible. Mathematical model of this isotherm is shown by Equation 3 (15, 16):
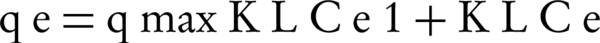
Where, qmax is the maximum adsorption capacity (mg /g), KL is the experimental constant (coefficient of Langmuir equation). Ce and qe parameters are similar to Freundlich isotherm.
3.3. BET Isotherm Model
This isotherm is based on the assumptions of Langmuir isotherm model and is also based on the assumption that adsorption is not single layered but is multi-layer. This isotherm states that when a layer of material is adsorbed by the adsorbent, another layer is also adsorbed on the adsorbent as well. The equation of this isotherm is as follows:
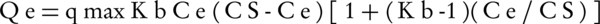
Where, Cs is the saturation concentration of soluble material (mg/L), Kb is a constant that is achieved by the linear equation and states the energy between the adsorbate and the surface of adsorbent. The more there is of this amount, the more there is adsorption energy.
qmax is the amount of adsorbate per unit of mass of adsorbent (g) to form a single molecular layer on the surface of adsorbent (mg/g).
3.4. Dubinin-Radushkevich Isotherm Model
Dubinin-Radushkevich model is usually used to estimate the porosity and free energy of adsorption. The model assumes that the adsorption porosity curves are related to the porosity of the adsorbent. The model equation is as follows:
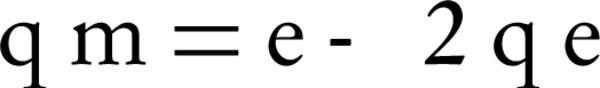
Where, qm is the adsorption capacity of a single-layer and β (constant of the equation) is the factor of porosity;ε is called Polanyi potential, which is defined by the following equation:
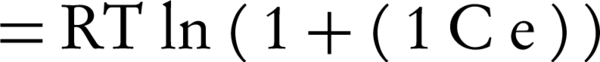
Where, R is the universal gas constant (8.314 J.K-1.mol-1), and T is the temperature (°K).
3.5. Temkin Isotherm Model
Temkin isotherm contains a factor that clearly shows the interactions between the adsorbent and adsorbate. In Temkin isotherm, it is assumed that the adsorption temperature of all molecules decrease when the surface of the adsorbent is more covered. Temkin isotherm is calculated using Equation 7.
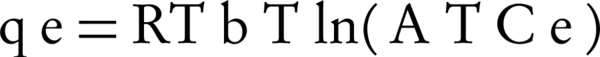
Where BT is Temkin’s constant and is expressed as J/mol and is related to the temperature of adsorption. AT is the constant of Temkin isotherm (L/g), R is the universal constant of gases and T is absolute temperature (°K). In the mentioned equations, the amount of B is usually calculated with Equation 8.
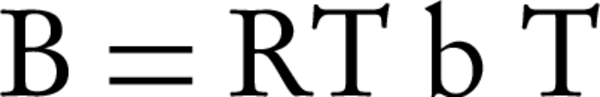
4. Results
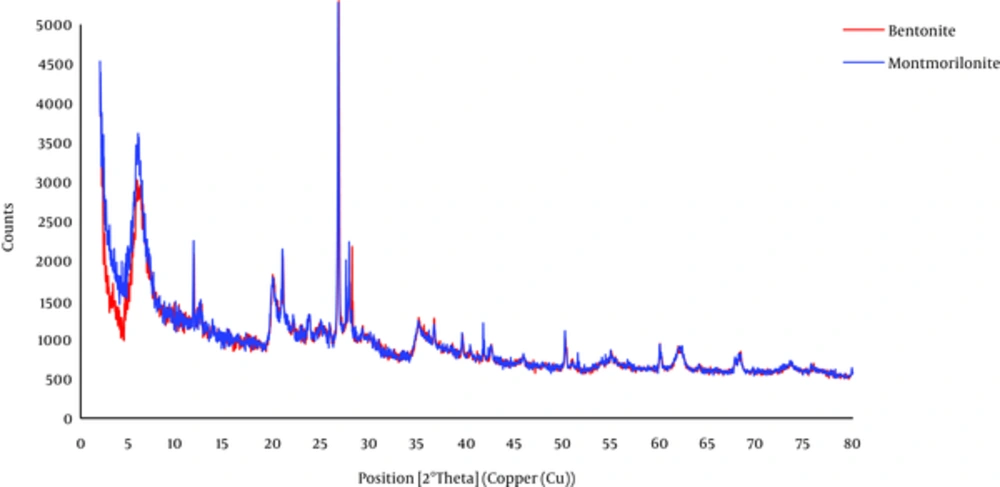
The scanning electron microscope (SEM) and x-ray Diffraction (XRD) spectra of bentonite and montmorillonite are shown in Figures 1 and 2, respectively.
Scanning Electron Microscope Pictures of A, Bentonite and B, Montmorillonite Nanoparticles
X-Ray Diffraction Spectra of A, Bentonite and B, Montmorillonite Nanoparticles
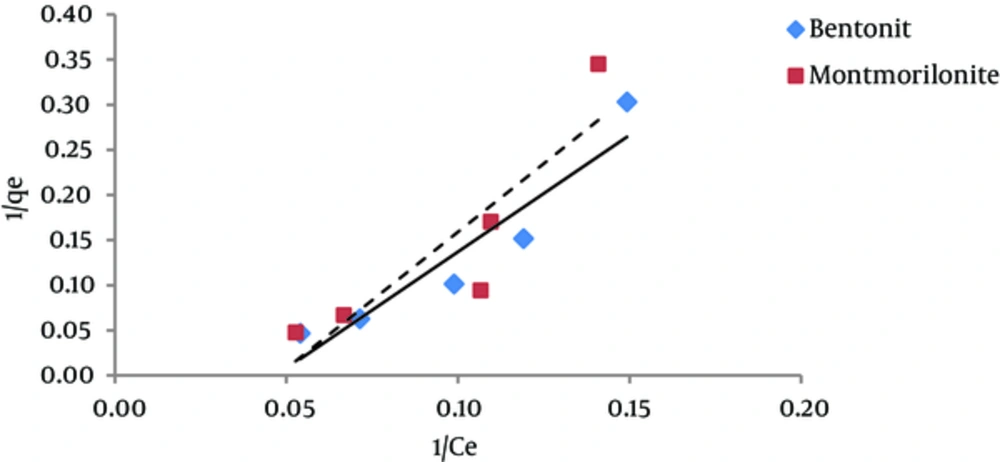
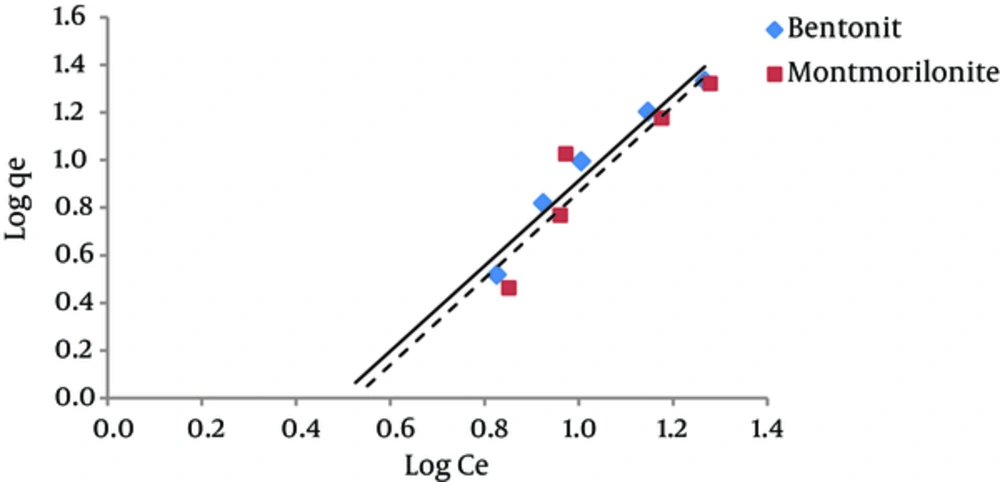
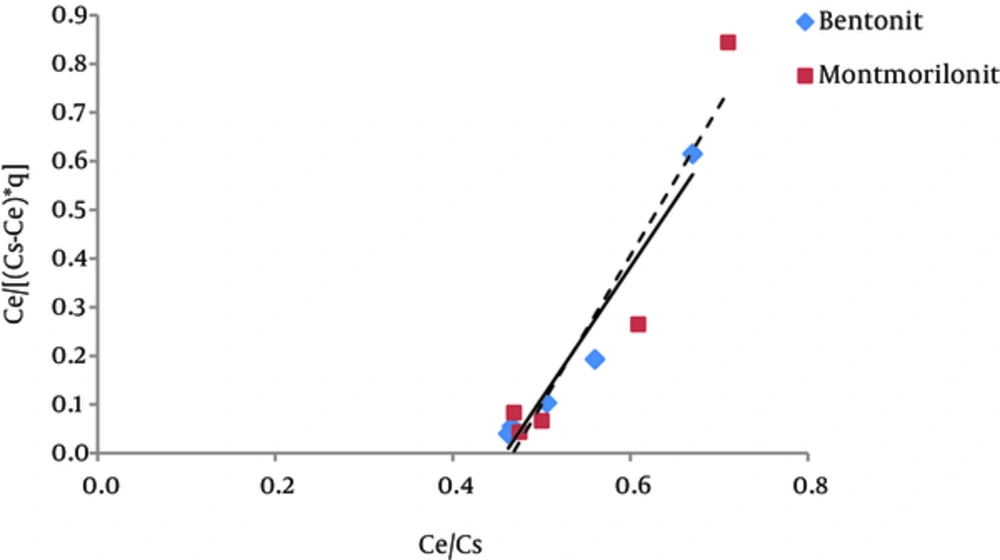
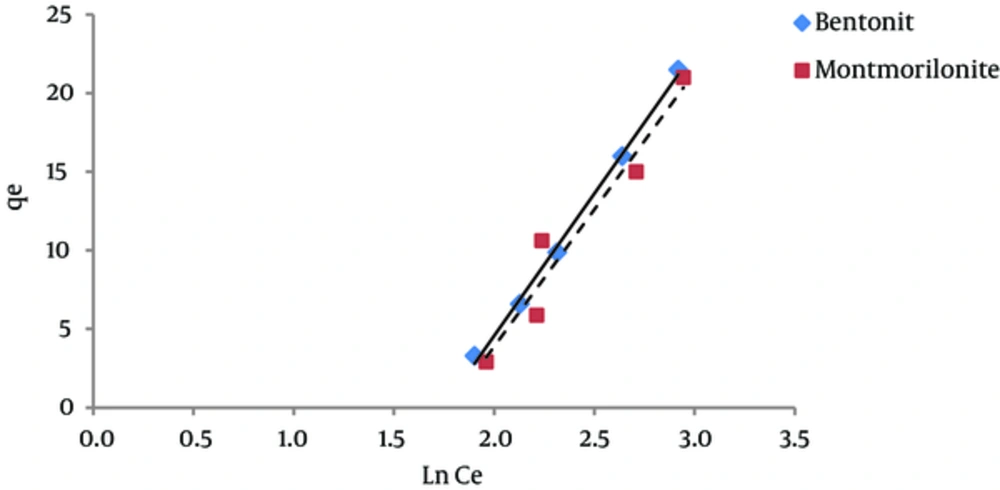
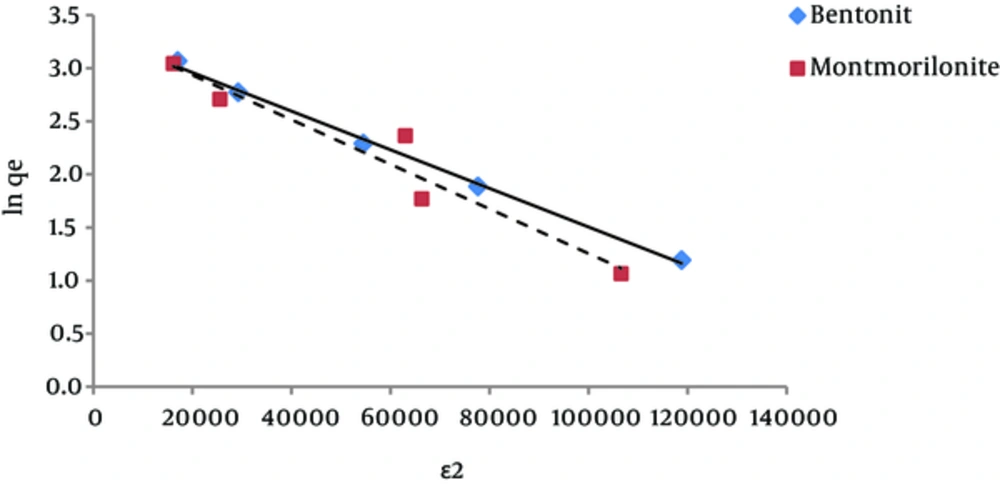
The results of studying the compliance of humic acid adsorption (by nano particles of bentonite and montmorillonite) with different isotherms are presented in Figures 3 to 7 and Table 1.
Compliance of Humic Acid Adsorption on Nanoclay with Langmuir Isotherm
Compliance of Humic Acid Adsorption on Nanoclay with Freundlich Isotherm
Compliance of Humic Acid Adsorption on Nanoclay with BET Isotherm
Compliance of Humic Acid Adsorption on Nanoclay with Temkin Isotherm
Compliance of Humic Acid Adsorption on Nanoclay With Dubinin-Radushkevich Isotherm
Constants and Regression Coefficients of Different Adsorption Isotherms for Adsorption of Humic Acid on Nanoclay
| Isotherms | Constants | Values | |
|---|---|---|---|
| Bentonit | Montmorillonit | ||
| Langmuir | qmax (mg/g) | 8.21 | 6.95 |
| KL (L/mg) | 0.05 | 0.06 | |
| RL | 0.26 | 0.22 | |
| R2 | 0.89 | 0.79 | |
| Freundlich | kf (mg/g) | 0.13 | 0.11 |
| 1/n | 1.79 | 1.81 | |
| n | 0.56 | 0.55 | |
| R2 | 0.96 | 0.86 | |
| BET | 1/A.Xm | 1.24 | 1.43 |
| (A-1)/(A.Xm) | 2.71 | 3.07 | |
| A | 4.37 | 5.40 | |
| Xm (mg/g) | 1.61 | 1.76 | |
| R2 | 0.95 | 0.90 | |
| Temkin | AT, L/mg | 0.17 | 0.17 |
| bT (J/mole) | 136.95 | 142.02 | |
| B | 18.09 | 17.45 | |
| R2 | 1.00 | 0.94 | |
| Dubinin-Radushkevich | β, mole2/kJ2 | 0.00 | 0.00 |
| E, kJ/mole | 0.17 | 0.15 | |
| qm, mg/g | 27.78 | 28.70 | |
| R2 | 1.00 | 0.93 | |
5. Discussion
The relationship between the concentration of adsorbed humic acid (by nano particles of bentonite and montmorillonite) and the final concentration in the solution is described by isotherms. Several isotherms are used to describe the characteristics of adsorption equilibrium.
From Figure 1 the nanoclay structure appears dense with nonporous particles. Furthermore, heterogeneous surface of the particles is clear. The XRD patterns of the bentonite and montmorillonite nanoparticles in Figure 2 show a medium peak at 2θ = 6.05° and 2θ = 5.97° for both nanoparticles, respectively, and also a sharp peak at 2θ = 27.80° and 2θ = 27.81° that corresponds with the nanostructures of the adsorbents.
According to the results of Figure 3, it is evident that due to the low regression coefficient, the behavior of humic acid adsorption onto bentonite and montmorillonite nanoparticles does not follow much to the Longmuir isotherm. According to Table 1, the regression coefficient (R2) for bentonite and montmorillonite nanoparticles is 0.79 and 0.89, respectively. Langmuir model estimated that the maximum amount of humic acid adsorption capacity (qmax) by bentonite and montmorillonite nanoparticles was 8.21 and 6.95 mg/g, respectively. These values were very different from the equilibrium capacity that was achieved by the experiment. The amounts of KL for the adsorption of humic acid by montmorillonite nanoparticles are more than the amounts of KL for adsorption of humic acid by bentonite nanoparticles. KL is a constant that increases when the size of adsorbent molecules is increased (17). According to the results of this study, the amount of KL for montmorillonite nanoparticles was more than the amount of KL for bentonite nano particles, which reflects the larger size of montmorillonite nanoparticles. Also, we studied the tendency of humic acid adsorption by a dimensionless parameter (RL), which is derived from the Langmuir model. If RL = 0, the adsorption is irreversible, if 0 < RL < 1, the adsorption is desirable, if RL = 1, the adsorption is linear and if RL > 1, then the adsorption is undesirable. According to the results of the Langmuir isotherm for adsorption of humic acid, the amounts RL for both adsorbents were between 0 and 1, so humic acid absorption by both adsorbents is desirable (18, 19).
According to Figure 4, the regression coefficient (R2) in Freundlich isotherm for both bentonite and montmorillonite nano particles was more than the R2 coefficient in Langmuir isotherm. The amount of KF in bentonite and montmorillonite nanoparticles was 0.13 and 0.11 (mg/g) (mg/ l) n, respectively. Therefore, due to the higher adsorption capacity of bentonite nanoparticles, the amount of KF is also higher for this nano particle. The 1/n parameter decreases when the adsorption power of the pollutant by the adsorbent increases. The amounts of 1/n for bentonite and montmorillonite nanoparticles were 1.79 and 1.8, respectively. These numbers indicate that humic acid adsorbed onto bentonite nanoparticles with more power in comparison with nano particles of montmorillonite. Other studies have reported similar results (20, 21).
According to Figure 5 regression coefficient, the BET isotherm provides a better description for humic acid adsorption on montmorillonite than the description that Langmuir and Freundlich isotherms provide for this process (adsorption of humic acid by montmorillonite). However, regarding humic acid adsorption by nanoparticles of bentonite, Freundlich and BET isotherms have approximately equal regression coefficients. According to Table 1, the amount of A parameter for Bentonite and montmorillonite nanoparticles was 4.4 and 4.5, respectively; thus, according to the BET isotherm, adsorption energy of humic acid adsorbed on montmorillonite is higher than the adsorption energy of humic acid adsorbed onto bentonite nanoparticles. The amount of Xm, which is the required amount of humic acid for the formation of a single molecule layer on the surface of the adsorbents (22), is 1.61mg/g for Bentonite nanoparticles and 1.76 mg/g for montmorillonite nanoparticles. Generally, BET isotherm has not been used much in different studies.
According to Figures 6 and 7, the amounts of the regression coefficient (R2) for Temkin and Dubinin Radushkevich isotherms for humic acid adsorption by bentonite nanoparticles were equal to one. The amounts of R2 in these two mentioned isotherms for humic acid adsorption by montmorillonite nanoparticles were higher than the amount of R2 for other isotherms. Therefore, it can be said with certainty that humic acid adsorption by nanoclay follows these two isotherms.
In the Temkin isotherm, AT is the bond constant that represents the maximum binding energy (L/mg) (23). The amount of AT for both bentonite and montmorillonite nanoparticles was 0.17 L/mg. The B index, which is related to the heat of adsorption for bentonite and montmorillonite nanoparticles, was 18.09 and 17.45 J/mole, respectively.
According to the Dubinin-Radushkevich isotherm, the amount of β (which is related to the adsorption energy), for bentonite and montmorillonite nanoparticles was 1.8×10-5 and 2.1×10-5 mole2/kJ2, respectively. This parameter gives an explanation about the average free energy or E. The average amounts of adsorption energy is achieved by the following equation (24):
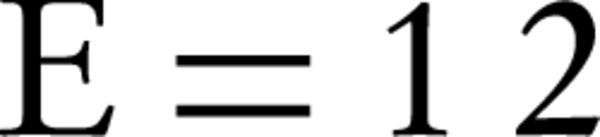
These values for humic acid adsorption by bentonite and montmorillonite nanoparticles were 0.17 and 0.15 kJ.mol-1, respectively. Whenever the value of E is between 8 and 16 kJmol-1, then it means that the adsorption is of chemical or ionic exchange type and if the value of E is between 1 and 8 kJmol-1, it means that adsorption has been carried out physically (23, 25). According to the results of this study, it was determined that the adsorption of humic acid by both nano-particles was physical. In addition, according to the amount of qmax that was obtained from the Dubinin Radushkevich isotherm, considering that this amount for bentonite and montmorillonite nanoparticles was 27.78 and 28.80 mg/g, respectively, it is expected for these amounts to be very close to the measured adsorption capacities that were obtained by adsorption experiments.
5.1. Conclusion
In this study, we examined the compatibility of the data of humic acid adsorption by bentonite and montmorillonite nanoparticles with five isotherm models. The results showed that the degree of compliance of humic acid adsorption by bentonite nanoparticles with these isotherms was as follow:
Langmuir isotherm < BET isotherm < Freundlich isotherm < Temkin isotherm = Dubinin Radushkevich isotherm. Also, the degree of compliance of humic acid adsorption by montmorillonite nanoparticles with these isotherms was as follow: Langmuir isotherm < Freundlich isotherm < BET isotherm < isotherm Dubinin Radushkevich < Temkin isotherm.
Acknowledgements
References
-
1.
Katsumata H, Sada M, Kaneco S, Suzuki T, Ohta K, Yobiko Y. Humic acid degradation in aqueous solution by the photo-Fenton process. Chem Eng J. 2008;137(2):225-30.
-
2.
Khorsandi H, Bina B, Amin MM. Removal of humic substances from water by advanced oxidation process using UV/TiO2 photo catalytic technology. J Water Wastewater. 2009;68:25-32.
-
3.
Naghizadeh A, Nasseri S, Mahvi AH, Rashidi A, Nabizadeh R, Kalantary R. Fenton regeneration of humic acid-spent carbon nanotubes. Desalin Water Treat. 2015;54(9):2490-5.
-
4.
Kamani H, Nasseri S, Khoobi M, Nabizadeh Nodehi R, Mahvi AH. Sonocatalytic degradation of humic acid by N-doped TiO2 nano-particle in aqueous solution. J Environ Health Sci Eng. 2016;14:3. [PubMed ID: 26819709]. https://doi.org/10.1186/s40201-016-0242-2.
-
5.
Kawasaki N, Ogata F, Yamaguchi I, Fujii A. Removal of orange II, methylene blue and humic acid by ozone-activated carbon combination (OZAC) treatment. J Oleo Sci. 2008;57(7):391-6. [PubMed ID: 18536508].
-
6.
Yu C, Jiang J. Comparative performance and computational approach of humic acid removal by clay adsorption. J Environment Protect. 2010;1(1):24.
-
7.
Koparal AS, Yildiz YS, Keskinler B, Demircioglu N. Effect of initial pH on the removal of humic substances from wastewater by electrocoagulation. Sep Purif Technol. 2008;59(2):175-82.
-
8.
Derakhshani E, Naghizadeh A. Ultrasound regeneration of multi wall carbon nanotubes saturated by humic acid. Desalin Water Treat. 2014;52(40-42):7468-72.
-
9.
Kamani H, Bazrafshan E, Ghanbari Ghozikali M, Askari M, Ameri R. Photocatalyst Decolorization of CI Sulphur Red 14 From Aqueous Solution by UV Irradiation in the Presence of ZnO Nanopowder. Health Scope. 2015;4(2).
-
10.
Naghizadeh A. Regeneration of Carbon Nanotubes Exhausted with Humic Acid Using Electro-Fenton Technology. Arab J Sci Eng. 2016;41(1):155-61.
-
11.
Litchfield DW, Baird DG. The role of nanoclay in the generation of poly (ethylene terephthalate) fibers with improved modulus and tenacity. Polymer. 2008;49(23):5027-36.
-
12.
Reynolds RJ. Atomic Absorption Spectroscopy. New York: Barnes and Noble Inc; 1970.
-
13.
Crittenden J, Trussell RR, Hand DW, Howe KJ, Tchobanoglous G. Water Treatment: Principles and Design. 3 ed. New York: John Wiley and Sons; 2012.
-
14.
Naghizadeh A, Nabizadeh R. Removal of reactive blue 29 dye by adsorption on modified chitosan in the presence of hydrogen peroxide. Environ Prot Eng. 2016;42(1):149-68.
-
15.
Safari GH, Zarrabi M, Hoseini M, Kamani H, Jaafari J, Mahvi AH. Trends of natural and acid-engineered pumice onto phosphorus ions in aquatic environment: adsorbent preparation, characterization, and kinetic and equilibrium modeling. Desalin Water Treat. 2015;54(11):3031-43.
-
16.
Ashrafi SD, Kamani H, Soheil Arezomand H, Yousefi N, Mahvi AH. Optimization and modeling of process variables for adsorption of Basic Blue 41 on NaOH-modified rice husk using response surface methodology. Desalin Water Treat. 2016;57(30):14051-9.
-
17.
Naghizadeh A. Comparison between activated carbon and multiwall carbon nanotubes in the removal of cadmium (II) and chromium (VI) from water solutions. Water Supply Res Tech Aqua. 2015;64(1):64-73.
-
18.
Su J, Lin HF, Wang QP, Xie ZM, Chen ZL. Adsorption of phenol from aqueous solutions by organomontmorillonite. Desalination. 2011;269(1):163-9.
-
19.
Ho YS, Porter JF, Mc Kay G. Equilibrium isotherm studies for the sorption of divalent metal ions onto peat: copper, nickel and lead single component systems. Water, Air, Soil Pollut. 2002;141(1-4):1-33.
-
20.
Shirzad Siboni M, Khataee A, Hassani A, Karaca S. Preparation, characterization and application of a CTAB-modified nanoclay for the adsorption of an herbicide from aqueous solutions: Kinetic and equilibrium studies. Comptes Rendus Chimie. 2015;18(2):204-14.
-
21.
Hassani A, Kiranşan M, Darvishi Cheshmehsoltani R, Khataee A, Karaca S. Optimization of the adsorption of a textile dye onto nanoclay using a central composite design. Turk J Chem. 2015;39(4):734-49.
-
22.
Naghizadeh A, Nasseri S, Rashidi AM, Rezaei Kalantary R, Nabizadeh R, Mahvi AH. Adsorption kinetics and thermodynamics of hydrophobic natural organic matter (NOM) removal from aqueous solution by multi-wall carbon nanotubes. Water Supply Water Sci Tech. 2013;13(2):273-85.
-
23.
Itodo AU, Itodo HU. Sorption Energies Estimation Using Dubinin-Radushkevich and Temkin Adsorption Isotherms. Life Sci J. 2010;7(4):31-9.
-
24.
Zheng H, Liu D, Zheng Y, Liang S, Liu Z. Sorption isotherm and kinetic modeling of aniline on Cr-bentonite. J Hazard Mater. 2009;167(1-3):141-7. [PubMed ID: 19171429]. https://doi.org/10.1016/j.jhazmat.2008.12.093.
-
25.
Jain M, Garg VK, Kadirvelu K. Chromium (VI) removal from aqueous system using Helianthus annuus (sunflower) stem waste. J Hazard Mater. 2009;162(1):365-72.