https://doi.org/10.17795/jhealthscope-12492

Adsorption of Methylene Blue Dye from Aqueous Solutions by Modified Pumice Stone: Kinetics and Equilibrium Studies

authors:

avatar Zahra Derakhshan 1 , avatar Mohammad Ali Baghapour 2 , * , avatar Mojdeh Ranjbar 1 , avatar Mohammad Faramarzian 2

Student Research Committee, Shiraz University of Medical Sciences, Shiraz, IR Iran
Department of Environmental Health Engineering, School of Health, Shiraz University of Medical Sciences, Shiraz, IR Iran
Health Scope: Vol.2, issue 3; 136-144
published online: November 3, 2013
article type: Research Article
received: May 27, 2013
revised: July 23, 2013
accepted: July 24, 2013

how to cite: Derakhshan Z, Baghapour M A, Ranjbar M, Faramarzian M. Adsorption of Methylene Blue Dye from Aqueous Solutions by Modified Pumice Stone: Kinetics and Equilibrium Studies. Health Scope. 2013;2(3): 136-144. https://doi.org/10.17795/jhealthscope-12492.

Abstract

Background:

Dyes are one of the most important industrial pollutants, especially in textile industries. Many methods have been proposed in order to remove color from wastewater among which, adsorption is more acceptable due to the ability for its use in the large scale.

Objectives:

The objective of this study was to investigate pumice as an inexpensive adsorbent for removal of Methylene Blue from aqueous solutions.

Materials and Methods:

In this work the Modified Pumice Stone has been applied for removal of the Methylene Blue dye from aqueous environments. The effect of pH, contact time, initial concentration and amount of adsorbent were considered. In order to investigate the mechanism of the adsorption process, several kinetic models including pseudo-first order, pseudo-second order and intra-particle diffusion were used. In addition, equilibrium data was fitted on to Langmuir, Freundlich, Temkin and Dubinin-Radushkevich models.

Results:

Results showed that the adsorption of the Methylene Blue was enhanced with increasing initial dye concentration, pH and contact time. The optimum pH was 10. The qmax for adsorption of methylene blue dye from the Langmuir model was 15.87 mg/g. Considering the values of R2 (0.999) and χ2, Freundlich isotherm model and pseudo-second order kinetic model had the best fitness.

Conclusions:

This study has demonstrated that the modified Pumice stone with HCl can be employed as effective and inexpensive adsorbent for the removal of Methylene Blue from aqueous environments.

1. Background

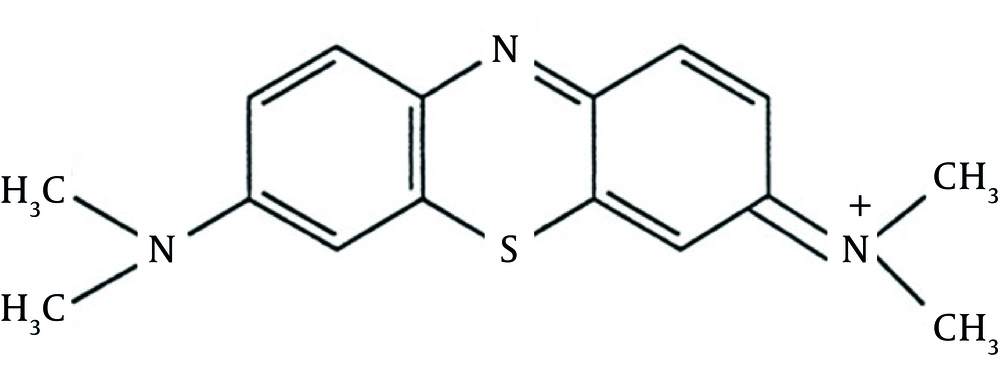
Industrial wastewater is considered as one of the major pollutants of the environment (1). Moreover, textile industries are among each country’s basic industries and have colored wastewater due to making use of colored materials (2). Overall, colored wastewater is produced by various industries, such as textile, dyeing, pharmaceutical, food, cosmetics and healthcare, paper, and leather industries. Such colors not only change the water’s color, which is important regarding aesthetics, but they also prevent light from penetrating through water, disturb photosynthesis, and destroy the aquatic ecosystem as well as several aquatic species (2, 3). One of the high consuming materials in the dye industry is Methylene Blue (MB) which is used for cotton and silk painting (4). Chemical structure of MB is illustrated in Figure 1 (3). Up to now, a great number of methods have been proposed in order to remove dyes from the industrial wastewater among which adsorption is the most acceptable due to its cost effectiveness and its capability to be used in large scales (5).

Molecular Structure of Methylene Blue
Molecular Structure of Methylene Blue
Figure 1.

Molecular Structure of Methylene Blue

The methods of color removal from industrial effluents include biological treatment, coagulation, flotation, adsorption, oxidation and hyper filtration (3, 4, 6, 7). Among the treatment options, adsorption has been found to be superior to other techniques for water treatment in terms of initial cost, simplicity of design, ease of operation and insensitivity of toxic substances (7). Different adsorbents have been used for the removal of various materials from aqueous solutions, such as dyes, metal ions and other organic materials including perlite (4, 6-8), bentonite (9), silica gels (10), fly ash (11), lignite (11), peat (12), silica (13), etc. Among these natural materials, pumice which is a volcanic stone has a low weight and a porous structure (up to 85%) and can be found in many regions of the world. Because of its micro-porous structure, pumice has a high specific surface area, which is advantageous since it allows avoidance of the preliminary step of calcinations, a high energy cost step, and can float in water owing to its low density. Recently, many researchers have used pumice for removal of cadmium (14), disinfection by-products (15), heavy metals (16), sulfur dioxide (17) and azo dye (2).

2. Objectives

Due to several advantages of the pumice stone and its accessibility in Iran, the aim of the present work was to investigate its effectiveness for the removal of MB at various experimental conditions. Since initial pumice has some impurity, shows low sorption capacity and is negatively charged (2), the acidic treated pumice was used in this work. Therefore, the purpose for acidic treatment of pumice was to improve the positive surface charge of adsorbent and its sorption capacity since initial pumice shows low sorption capacity. The present study aims to use modified Pumice stone for removing MB dye from aqueous solutions.

3. Materials and Methods

3.1. Instruments and Reagents

Stock solution was prepared by dissolving the required amount of MB in double distilled water. The test solutions were prepared by diluting stock solution to the desired concentrations. The concentration of the MB was determined at 620 nm. The pH measurements were done using pH/Ion meter (Metrohm model-827, Swiss) and adsorption studies were carried out on DR-5000 spectrophotometer (HACH, U.S.A). All chemicals included NaOH, HCl and MB with the highest available purity and were purchased from Merck, Darmstadt, Germany. All solutions were stirred on a hotplate and stirrer (JENWAY, model-1000, U.K).

3.2. Adsorbent Features

Pumice, foam, firefighting foam and pumicite are siliceous glasses which are mostly light color and are usually created through the accumulation of volcanic flows. In the present experimental study, pumice samples as adsorbents were gathered from Ghorveh, Kurdistan, Iran. The chemical structure of this stone is presented in Table 1 (2, 14, 17). As Table 1 depicts, silicon and aluminum oxides comprise a major part of the utilized adsorbent, which shows the high capability of this adsorbent for absorption process as well as ion exchange.

Table 1.

Chemical Structure of Pumice Stone

Chemical CompositionPercent
SiO269.75
Al2O312.43
Fe2O31.88
CaO1.70
MgO0.12
NaO23.58
K2O4.47
TiO21.54
Other4.53

3.3. Preparing the Adsorbent

At first, pumice mineral cartridge was washed several times by de-ionized water in order to remove the primary impurities. Next, the mineral cartridge was placed in HCl 1 N for 24 hours for increasing the adsorbent’s porosity. Afterwards, the mineral cartridge was washed several times by de-ionized water and this was continued until the effluent’s turbidity reached below 0.1 NTU. Finally, the prepared sample was grinded and mesh 20 with the effective size of 2 mm was utilized as the adsorbent.

3.4. Adsorption Study

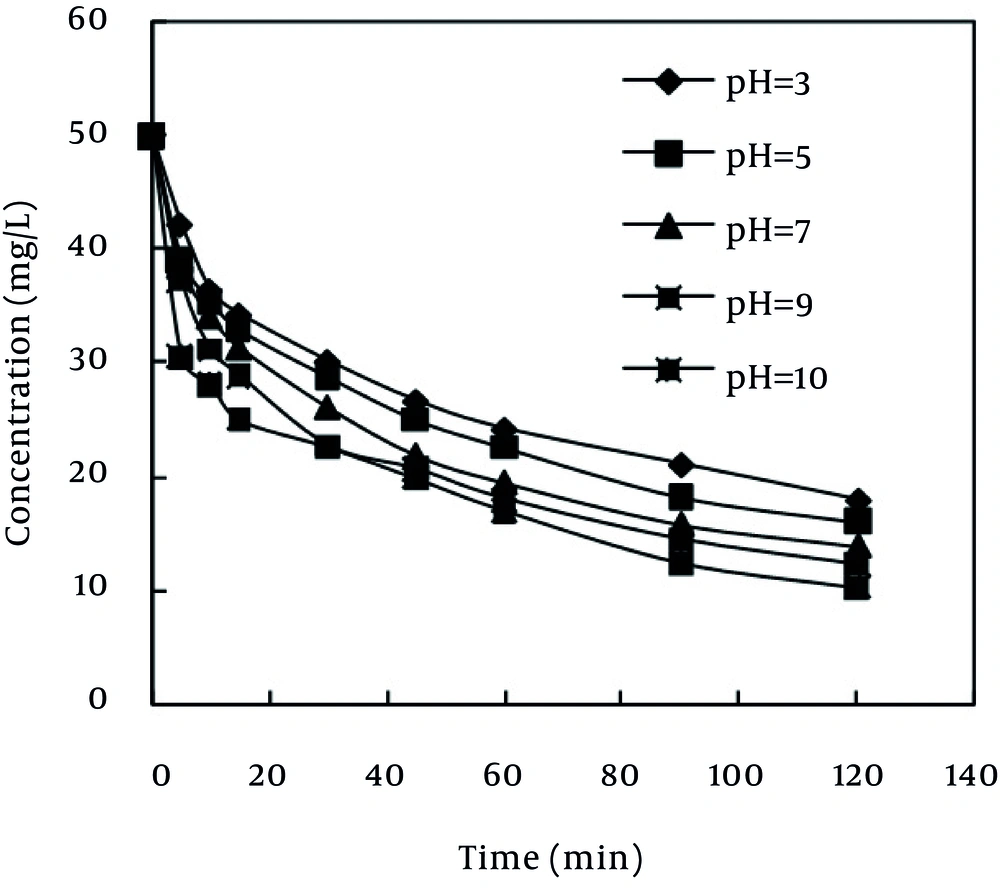
To study the effect of important parameters like the pH, contact time and initial dye concentration on the adsorptive removal of MB, batch experiments were conducted. For each experimental run, 50 cc of different concentrations of the dye solution (30 - 60 mg/L) was agitated with 0.2 g of the adsorbent at 100 rpm until the equilibrium was achieved. Samples were withdrawn at different time intervals (0, 5, 15, 30, 60, 90 and 120 minutes for MPS) and kinetics, isotherm and other parameters of adsorption was determined by analyzing the remaining dye concentration from aqueous solution. In order to evaluate the effect of the initial pH on MB adsorption, the equilibrium study was conducted at different pH levels 3, 5, 7, 9 and 10, and other equilibrium studies were continued at the optimum pH = 10. The pH of the solutions was adjusted by adding 0.1 N aqueous solution of NaOH and HCl.

The percentage removal of dye was calculated using the following equation (1, 18):

1) %MB Removal = (C0 - Ct) / C0 × 100

Where C0 (mg/L) and Ct (mg/L) are the initial dye concentration and dye concentration at time t, respectively. When the system reached the equilibrium concentration, the equilibrium adsorption capacity was calculated through the following equation (2, 19):

2) qe = v (C0-Ce)/w

In this equation, qe (mg/g) represents the rate of the adsorbed dye per mass unit of the absorbent, C0 (mg/L) and Ce (mg/L) are initial and equilibrium dye concentrations, respectively, and v (L) and w (g) are the volume of the dye solution and the weight of the adsorbent, respectively.

4. Results

4.1. The Effect of pH on Removal Efficiency

Solution pH affects both aqueous chemistry and surface binding sites of the adsorbents. The effect of initial pH on adsorption of MB was studied from pH 3 to 10 at initial MB concentration of 50 mg/L, adsorbent dosage of 0.2 g and contact time of 120 min. Two possible mechanisms of adsorption of MB on the MPS adsorbent may be considered include: (a) electrostatic interaction between the adsorbent and the MB molecule, (b) a chemical reaction between the MB and the adsorbent. When pH increases, the concentration of OH¯ ions in the desired solution is increased, as well. This causes the surface of the MPS to become deprotonated and, as a result, the negative charge of the used MPS surface will be amplified. Therefore, the electrostatic attractive force between the MB dye, which has a positive charge, and the adsorbent surface increases, and consequently, the rate of dye adsorption increases, as well (20). As Figure 2 depicts, as the pH of the solution increased from 3 to 10, the rate of removal also increased, which is consistent with the results obtained by El-Qada et al. (21), Chen et al. (22), and Karagoz et al. (23).

The Effect of pH on the Removal of MB Dye
The Effect of pH on the Removal of MB Dye
Figure 2.

The Effect of pH on the Removal of MB Dye

4.2. The Effect of Contact Time on the Removal of MB Dye

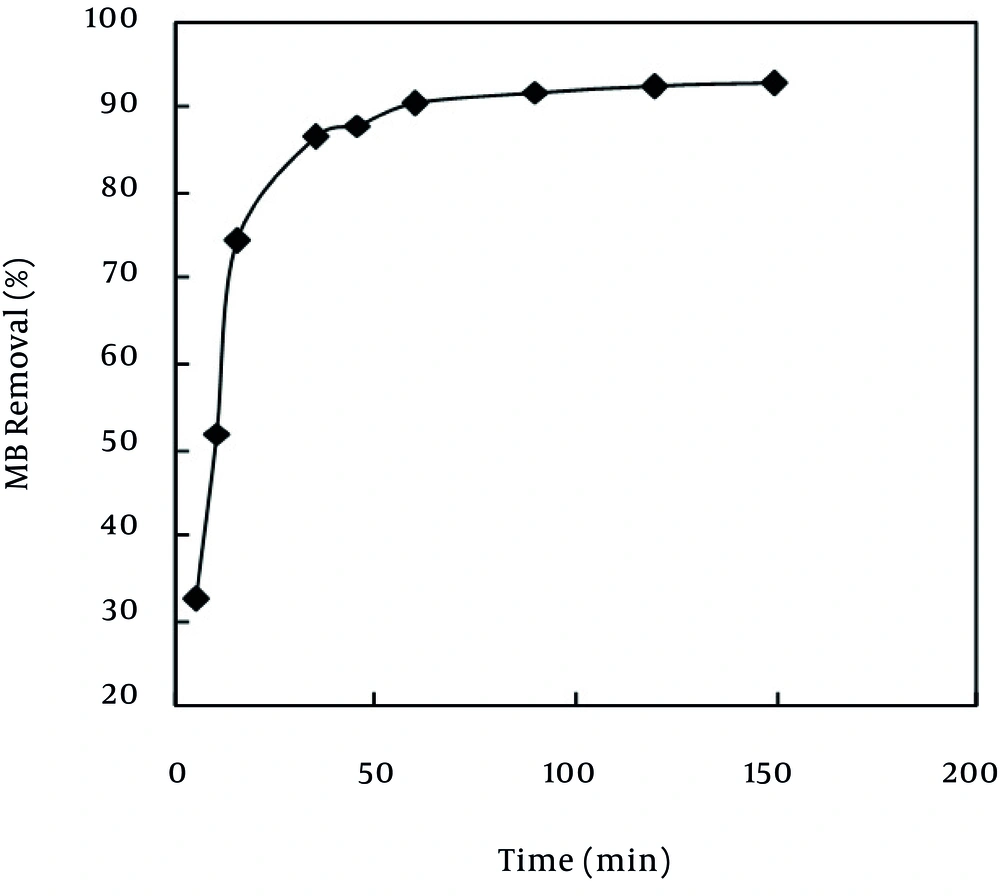
Generally, diffusion of the adsorbate on the used adsorbent and ultimately the adsorption phenomena on the adsorbent are time consuming processes (24). The adsorption rate, obtained for MB adsorption on MPS was observed by decrease of the concentration of MB within the adsorption medium with contact time. The time necessary to reach the equilibrium for the removal of the MB molecules at different concentrations (30 - 60 mg/L) by MPS from aqueous solution was established to be about 120 minutes. As Figure 3 shows, at all the used concentrations, as the contact time between the adsorbent and the adsorbate increased, the adsorption rate increased, as well. According to Figure 3, the highest rate of MB removal took place during the 0 - 20 minute interval. In the remaining concentrations, this reduction continued up to 60 minutes with a lower slope. From this time up to 120 minutes, the system was almost constant and did not have much adsorption. At 50 mg/L of MB, the removal rate varied from 32.6% to 92.3% of the maximum removal onto MPS. For instance, the adsorbents exhibited three stages, which can be attributed to each linear portion of the figure. The first linear portion was attributed to the diffusion process of MB to the adsorbent surfaces (2, 9), hence, was the fastest sorption stage. This result is corroborated by the factionary-order kinetic model. The second linear portion was attributed to intra-particle diffusion, which was a delayed process. The third stage may be regarded as the diffusion through smaller pores, which is followed by the establishment of the equilibrium (2, 9). The surface of MPS may contain a large number of active sites and the solute uptake can be related to the active sites on equilibrium time. The higher sorption rate at the initial period (first 120 minutes) may be due to an increased number of vacant sites available at the initial stage. As a result there exists increased concentration gradient between adsorbate in solution and adsorbate in adsorbent surface. This increase in the concentration gradients tends to increase in MB sorption at the initial stages.

The Effect of Contact Time on the Removal Rate of MB Dye at pH = 10, C0 = 50 mg/L
The Effect of Contact Time on the Removal Rate of MB Dye at pH = 10, C0 = 50 mg/L
Figure 3.

The Effect of Contact Time on the Removal Rate of MB Dye at pH = 10, C0 = 50 mg/L

4.3. The Effect of Initial Concentration on MB Removal Efficiency

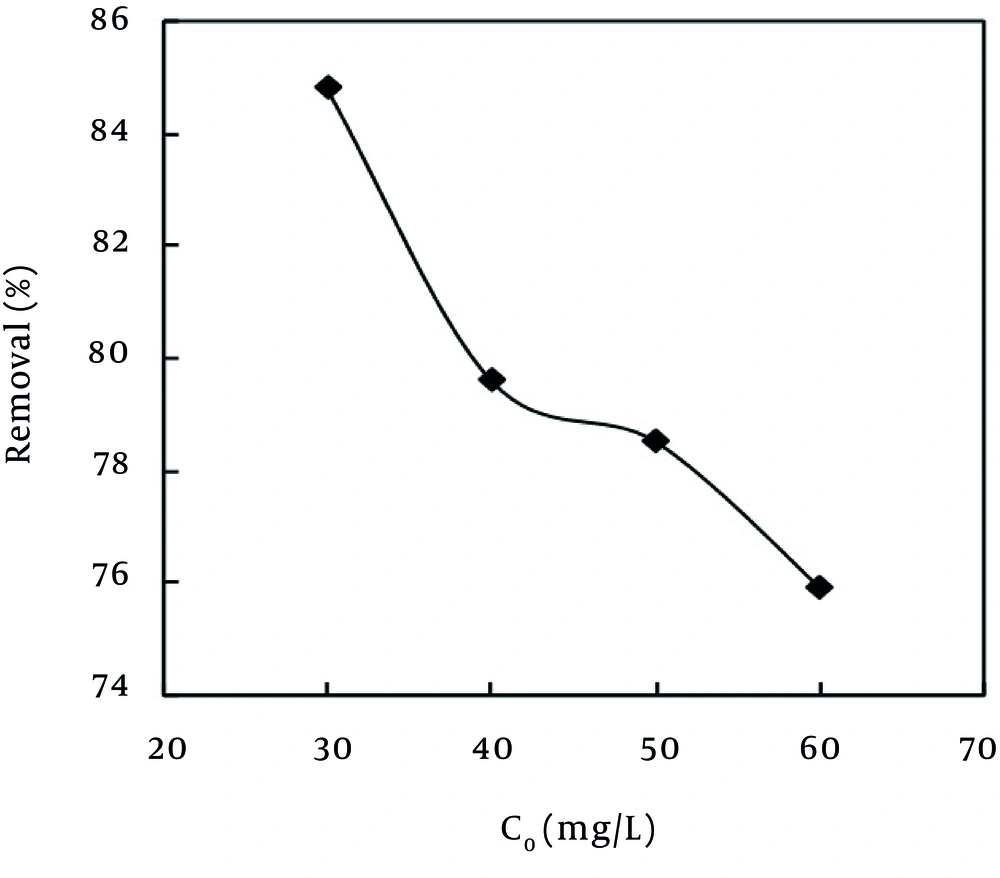
The effect of the initial concentration of MB dye on the adsorption efficiency of the MPS was evaluated at different concentrations of 30, 40, 50, and 60 mg/L. As Figure 4 depicts, one of the effective factors on the rate of dye uptake was the initial dye concentration of MB. In the present study, with the increase of the initial concentration from 30 mg/L to 60 mg/L, the rate of dye removal was reduced from 84.8% to 75.9%. In addition, as the pollutant concentration increased in the aquatic environment, the number of available sites on the adsorbent surface decreased. In other words, with the decrease of the pollutant concentration in the aquatic environment, molecules of the adsorbate have more chance to react with the available active sites on MPS and, as a result, the adsorption rate is increased. Hence, one can claim that one method to increase the percentage of dye removal is dilution of wastewater (25).

The Effect of Initial Concentration (30 - 60 mg/L) on MB Dye Removal Percentage at pH = 10 and Contact Time of 120 Minutes
The Effect of Initial Concentration (30 - 60 mg/L) on MB Dye Removal Percentage at pH = 10 and Contact Time of 120 Minutes
Figure 4.

The Effect of Initial Concentration (30 - 60 mg/L) on MB Dye Removal Percentage at pH = 10 and Contact Time of 120 Minutes

4.4. Adsorption Isotherm

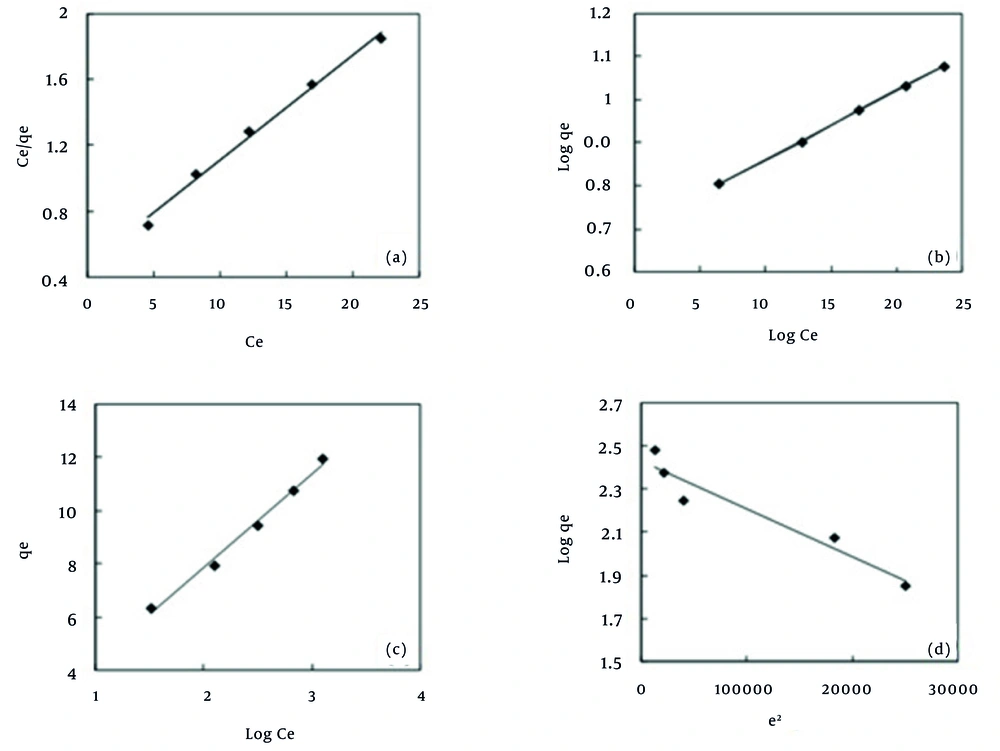
Adsorption isotherms are prerequisites to understand the nature of the interaction between adsorbate and the adsorbent used for the removal of organic pollutants. An adsorption isotherm describes the relationship between the amount of adsorbate up taken by the adsorbent and the adsorbate concentration remaining in solution (26). There are many equations for analyzing experimental adsorption equilibrium data. The equation parameters of these equilibrium models often provide some insight into the adsorption mechanism, the surface properties and affinity of the adsorbent for adsorbate (26-28). The parameters obtained from different models provide important information on the surface properties of the adsorbent and its affinity for the adsorbate. In present study, Langmuir, Freundlich, Temkin, and Dubinin-Radushkevich (D-R) isotherms were utilized in order to analyze the MB adsorption by the MPS. The equations and the linear forms of these models are presented in Table 2 (7, 12, 14), and the results are shown in Table 3.

Table 2.

Isotherm Models and Their Linear Forms

ModelNonlinear FormLinear FormNumber of Equation
Langmuirqe= qmaxkLCe/(1 + KL) CeCe/qe= (1/bqmax) + (1/qmax) Ce3
Freundlichqe= KFCe1/nLog qe= Log KF+ (1/n) log Ce4
Temkinqe= RT/bt (ln (atCe))qe= A + B ln Ce5
Dubinin-Radushkevich-lnQ = lnQm– k [RT ln (1+(1/Ce)) ] 2 E = -(2k)-0.56

In the equations presented in Table 2, qmax (mg/g) is the maximum adsorption capacity of the adsorbent, KL (L/mg) is the Langmuir constant, n and KF (L/mg) are the Ferundlich constants and the intensity of adsorption, respectively, Q (mg/g) is the amount of MB dye adsorbed per unit mass of the adsorbent, Qm (mg/g) is the capacity of the intended adsorbent, R (8.314 J/mol.K) is the universal gas constant, T (K) is the absolute temperature, K is the Dubinin–Radushkevich model constant (mol2/kJ2). E, is the mean adsorption energy and A ((RT/bt) 1nat) and B (RT/bt) are the constants of Temkin isotherm (4, 6, 20, 21).

The Langmuir equation is valid for monolayer adsorption onto a completely homogenous surface with a finite number of identical sites with negligible interaction between adsorbed molecules (26). Figure 5 shows the Langmuir (Ce/qe vs. Ce) plots for adsorption of MB. RL, and the correlation coefficients for the Langmuir isotherm are presented in Table 3. The essential features of the Langmuir isotherm may be expressed in terms of equilibrium parameter RL, which is a dimensionless constant referred to as a separation factor or equilibrium parameter:

7) RL = 1/(1 + KLC0)

where C0 is the initial concentration and KL is the constant related to the energy of adsorption (Langmuir constant). The values of RL indicate the type of isotherm to be irreversible (RL = 0), favorable (0 < RL< 1), linear (RL = 1) or unfavorable (RL > 1). Value of separation for adsorbent is found to be less than unity, confirming thereby the favorable adsorption process. The isotherms of MB on MPS were found to be linear for the entire concentration range studies and the correlation coefficients were extremely high (R2 > 0.99) as shown in Table 3. As Table 3 shows, the maximum adsorption capacity of the MPS in the Langmuir model was obtained as 15.87 mg/g which is considered as a favorable rate compared to other similar studies (Table 4) (29-32). The Freundlich isotherm (33) is derived by assuming a heterogeneous surface with a non-uniform distribution of sorption heat over the surface. Figure 5 shows the Freundlich (log qe vs. log Ce) plots for adsorption of MB. Table 3 shows the Freundlich adsorption isotherm constant and its respective correlation coefficients. Heat of adsorption and the adsorbent–adsorbate interaction on adsorption isotherms were studied by the Temkin isotherm (34). Figure 5 shows the Temkin (qe vs. ln Ce) plots for adsorption of MB. The constants obtained for the Temkin isotherm are shown in Table 3. Langmuir and Ferundlich isotherms do not provide any information about the surface adsorption mechanism. Therefore, other isotherm models, such as Dubinin-Raduchkevich, are used for estimating the mechanism of surface adsorption. Raduchkevich in 1949 and Dubinin in 1965 proposed that the adsorption curve depends on the structure of the adsorbent pores (35). The plot of ln qe vs. ε2 at for MB is presented in Figure 5. The constant obtained for D–R isotherms are shown in Table 3. The mean adsorption energy (E) gives information about the chemical and physical nature of adsorption (36).

Langmuir (a), Freundlich (b), Temkin (c) and Dubinin- Radushkevich (d) Isotherm Models Plots for the Adsorption of MB Concentrations (30-60 mg/L), with Optimum Conditions: MPS Amount (0.2 g/50 mL), Contact Time 120 Minutes and pH = 10
Langmuir (a), Freundlich (b), Temkin (c) and Dubinin- Radushkevich (d) Isotherm Models Plots for the Adsorption of MB Concentrations (30-60 mg/L), with Optimum Conditions: MPS Amount (0.2 g/50 mL), Contact Time 120 Minutes and pH = 10
Figure 5.

Langmuir (a), Freundlich (b), Temkin (c) and Dubinin- Radushkevich (d) Isotherm Models Plots for the Adsorption of MB Concentrations (30-60 mg/L), with Optimum Conditions: MPS Amount (0.2 g/50 mL), Contact Time 120 Minutes and pH = 10

Table 3.

Constants and Correlation Coefficients of Isotherm Models

ParameterValues
Langmuir
KL(L/mg)0.132
Qm(mg/g)15.87
R20.992
RL0.131
χ21.87
Freundlich
1/nf0.458
(L/mg) KF3.45
R20.999
χ20.12
Temkin
KT(L/mg)1.24
BT3.535
bt712.63
R20.990
χ21.56
Dubinin-Radushkevich
Qm(mg/g)11.376
K×10-62
E (KJ/mol)0.5
R20.926
χ25.41
Table 4.

Comparison of the Capacity of Monolayer Adsorption in This Study and Other Similar Studies

Type of AdsorbentRemoved MaterialAmount of Adsorption Per Mass Unit of the Adsorbent, qe, mg/gReferences
Pumice powder (I)Methylene blue0.442(29)
Pumice powder (II)Methylene blue1.488(29)
PumiceFluoride41(30)
Pumice granuleAzo dye0.024(32)
Pumice granulesFluoride2(31)
Modified pumice with hydrochloric acidMethylene blue15.87The present study

As Table 3 depicts, MB dye adsorption on the MPS has a high compliance with the Freundlich model (R2 = 0.999). This shows that the surface of the adsorbent is heterogeneous and the adsorption of MB dye on the adsorbent is multilayer. This finding is in line with the results that reported previously by El-Qada at al. (21) and Altenor et al. (37). Also, in this study, the value of n coefficient in the Freundlich model was found to be 2.182 which indicate a high tendency toward adsorbing the MB dye onto the MPS and this fact had been demonstrated by RL in advance. The coefficient 1/n in the Freundlich model is a value between 0 - 1 which represents the adsorption intensity of adsorbate to adsorbent. In the present study, 1/n was revealed as 0.458 which indicates the favorable adsorption of the adsorbate (37).

4.5. Adsorption Kinetics

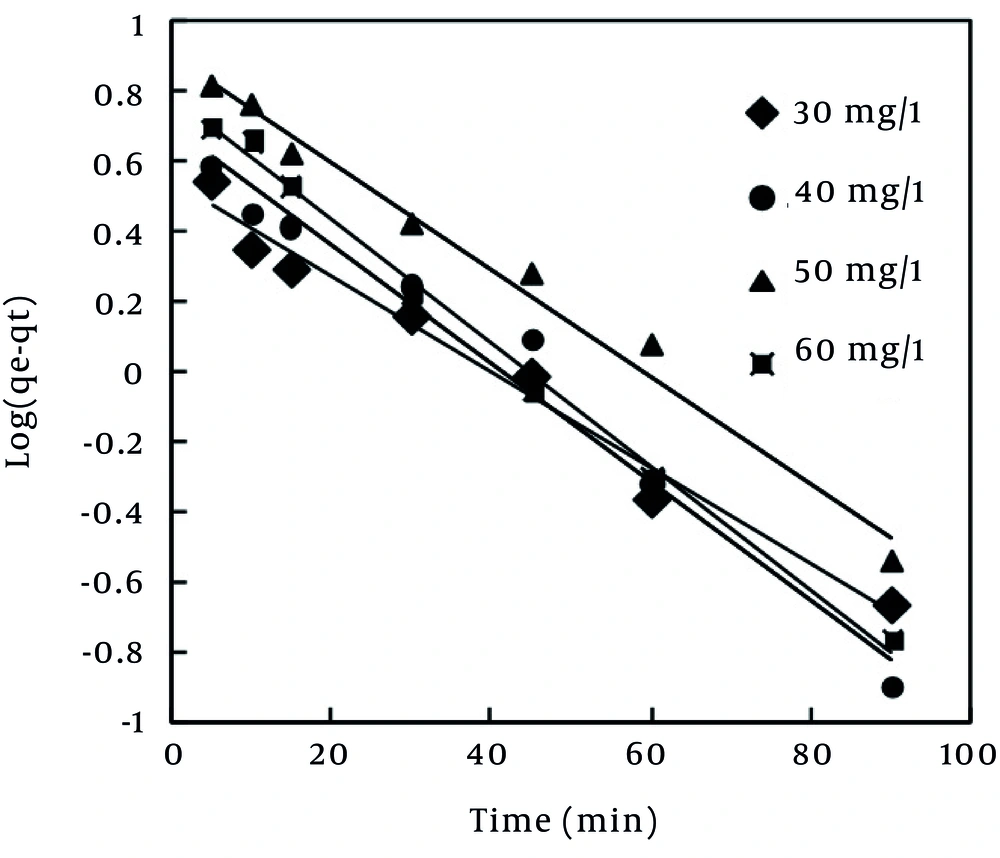
The rate and mechanism of the adsorption process can be elucidated based on kinetic studies. Dye adsorption on solid surface may be explained by two distinct mechanisms: (1) An initial rapid binding of dye molecules on the adsorbent surface; (2) relatively slow intra-particle diffusion. To analyze the adsorption kinetics of the dye, the pseudo-first-order, the pseudo-second-order, and intra-particle diffusion models were applied (38, 39). Each of these models and their linear modes of theme are shown in Table 5 (2, 31). In the equations presented in Table 5, qe and qt refer to the amount of dye adsorbed (mg/g) at equilibrium and at any time, t (min), respectively and K1 (1/min), K2 (g/mg.min) are the equilibrium rate constants of pseudo-first order and pseudo-second order models, respectively. Kdif is the intra-particle diffusion rate constant and values of C in intra-particle diffusion model give an idea about the thickness of the boundary layer.

Table 5.

Kinetic Models and Their Linear Forms

ModelNonlinear FormLinear FormNumber of Equation Group
Pseudo-first-orderdqt/dt= k1(qe-qt)ln (qe-qt) = ln qe-k1t8
Pseudo-second-orderdqt/dt= k2(qe-qt)2t/qt= 1/k2qe2+ (1/qe)t9
Intra-particle diffusionqt= kpt1/2+ C-10

Pseudo-first order model is a simple kinetic model, which was proposed by Lagergren (40) during 1898 and is used for estimation of the surface adsorption reaction rate. In order to obtain the rate constant of pseudo-first order reaction, linear pseudo-first order equation proposed by Lagergen and Svenska was used (Table 5). The values of ln (qe - qt) were linearly correlated with t. The plot of ln (qe - qt) vs. t should give a linear relationship from which the values of K1 were determined from the slope of the plot (Figure 6). In many cases, the first-order equation of Lagergren does not fit well with the entire range of contact time and is generally applicable over the initial stage of the adsorption processes (41). The value of R2 obtained for pseudo-first order model (Table 6) showed that MB dye adsorption on the MPS did not follow this model.

Pseudo-First-Order Kinetic Model Plot for the Adsorption of MB Concentrations
Pseudo-First-Order Kinetic Model Plot for the Adsorption of MB Concentrations
Figure 6.

Pseudo-First-Order Kinetic Model Plot for the Adsorption of MB Concentrations

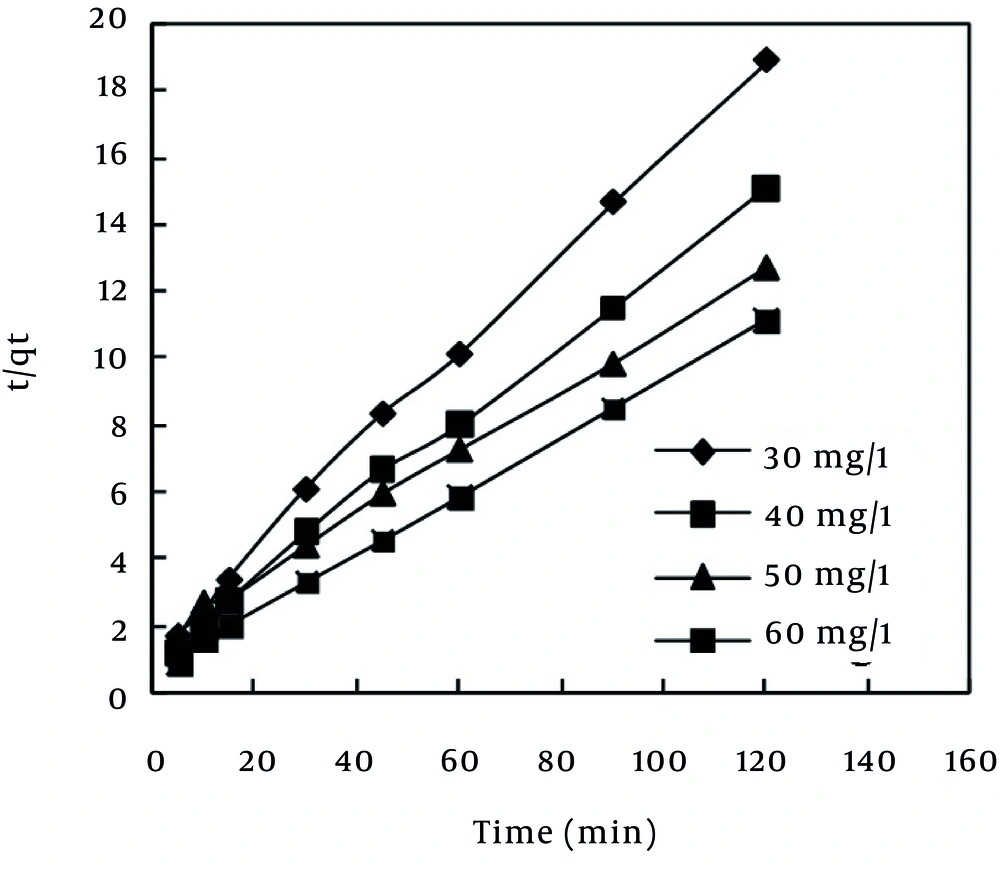
In the pseudo-second order model (42), the slope and intercept of the t/qt vs. t plot were used to calculate the second-order rate constant, K2 (Figure 7). The values of equilibrium rate constant (K2) are presented in Table 6. According to Table 6, the value of R2 (0.999) related to the pseudo-second order model revealed that MB dye adsorption followed this model, which is in agreement with the results obtained by Karagoz et al. (23), Hameed et al. (24), and Altenor et al. (37).

Pseudo-Second-Order Kinetic Model Plot for the Adsorption of MB Concentrations
Pseudo-Second-Order Kinetic Model Plot for the Adsorption of MB Concentrations
Figure 7.

Pseudo-Second-Order Kinetic Model Plot for the Adsorption of MB Concentrations

Table 6.

Constants and Correlation Coefficients of Adsorption Kinetics

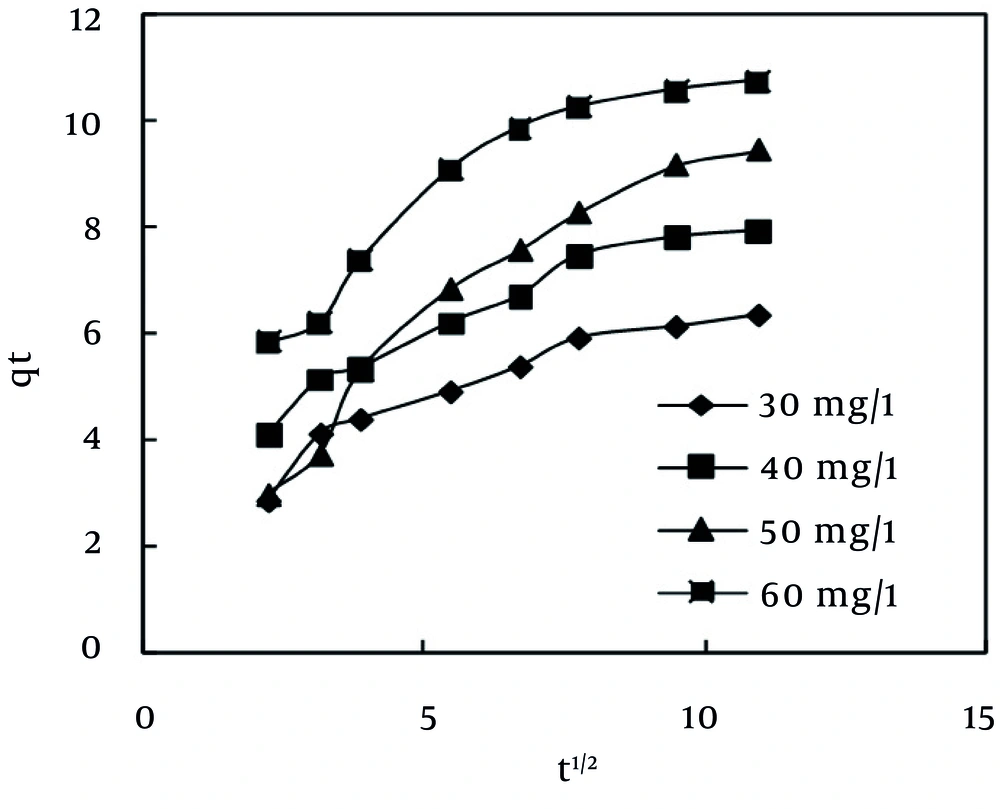
Kinetics modelsInitial Concentration of MB Dye(mg/L)
30405060
First-order kinetick10.0290.0370.039
qe(calc)3.4934.9456.081
R20.9790.9750.995
Second-order kinetick20.0170.0140.012
qe(calc)6.7568.47411.494
R20.9970.9970.999
h0.8031.0451.597
Intra particle diffusionKdiff0.3660.4400.612
C2.7413.6214.964
R20.9050.9430.887

Nevertheless, pseudo-first order and pseudo-second order kinetic models cannot identify the mechanism of diffusion of dye into the adsorbent pores. Therefore, intra-particle diffusion model (43), which is mostly used for expression of the dependence of surface adsorption process on time, was investigated. Plot of qt vs. t0.5 is illustrated in Figure 8. It shows two separate regions, the initial part is attributed to bulk diffusion while the final part to intra-particle diffusion. The value of R2 (Table 6) computed for intra-particle diffusion kinetic model showed that the rate of MB adsorption process was not controlled by the stage of diffusion of the adsorbate in the particles of the MPS (44). As Table 6 shows, Pseudo-second order is the best kinetic model, which can describe the adsorption of MB dye by the MPS. This finding is in line with the results that have been reported previously (2, 24, 37).

Intra-Particle Diffusion Model Plot for the Adsorption of MB Concentrations
Intra-Particle Diffusion Model Plot for the Adsorption of MB Concentrations
Figure 8.

Intra-Particle Diffusion Model Plot for the Adsorption of MB Concentrations

4.6. Error Analysis

In the single-component isotherm studies, the optimization procedure requires an error function to be defined in order to be able to evaluate the fit of the isotherm to the experimental equilibrium data. However, the use of R2 is limited for solving the linear forms of the isotherm equation, but not the errors in isotherm curves. In this study, a Chi-square test was used. The Chi-square test statistic is basically the sum of the squares of the differences between the experimental data and data obtained by calculation from models, with each squared difference divided by the corresponding data obtained by calculation from models (45). The equivalent mathematical statement is:

11) X2 = ∑i=1m (qe,exp – qe,calc)2 / qe,exp

Where qe,exp is the experimental data of the equilibrium capacity (mg/g), qe,calc is the equilibrium capacity obtained by calculating from the model (mg/g). Therefore, it is necessary to analyze the data set using the Chi-square test to confirm the best-fit isotherm for the adsorption of MB on MPS. Given the values of R2, and χ2 in Table 3 it can be concluded that the Freundlich isotherm model has the best goodness of fit among the applied isotherm models.

5. Discussion

The present study investigated the efficiency of MPS as a cheap adsorbent and the results revealed that MPS was an appropriate adsorbent for removing MB from the aquatic environments. pH also plays a major role in removing the MB. The findings of the present study also showed that as the contact time increased, the dye’s primary concentration as well as the dose of the intended adsorbate of the adsorption efficiency increased, as well. Adsorption equilibrium data follows Langmuir, Freundlich, Temkin and Dubinnin-Radushkevich isotherm models. The equilibrium data fitted very well in the Freundlich isotherm equation. The kinetic study of MB on to MPS was performed based on pseudo-first-order, pseudo-second-order and intra-particle diffusion equations. The data indicate that the adsorption kinetics follow the pseudo-second-order rate. This study concludes that the MPS could be employed as an appropriate, inexpensive, accessible and low-cost adsorbent for the removal of MB from aquatic environments.

Acknowledgements

References

  • 1.

    Sapci Z, Ustun B. The removal of color and COD from textile wastewater by using waste pumice. Elec J Environ Agric Food Chem. 2003;2(2):286-90.

  • 2.

    Samarghandi MR, Zarrabi M, Sepehr MN, Amrane A, Safari GH, Bashiri S. Application of acidic treated pumice as an adsorbent for the removal of azo dye from aqueous solutions: kinetic, equilibrium and thermodynamic studies. Iranian J Environ Health Sci Eng. 2012;9(1):9. [PubMed ID: 23369579]. https://doi.org/10.1186/1735-2746-9-9.

  • 3.

    Iqbal MJ, Ashiq MN. Adsorption of dyes from aqueous solutions on activated charcoal. J Hazard Mater. 2007;139(1):57-66. [PubMed ID: 16849033]. https://doi.org/10.1016/j.jhazmat.2006.06.007.

  • 4.

    Yang J, Qiu K. Preparation of activated carbons from walnut shells via vacuum chemical activation and their application for methylene blue removal. Chem Eng J. 2010;165(1):209-17.

  • 5.

    Robinson T, McMullan G, Marchant R, Nigam P. Remediation of dyes in textile effluent: a critical review on current treatment technologies with a proposed alternative. Bioresour Technol. 2001;77(3):247-55. [PubMed ID: 11272011].

  • 6.

    Santhy K, Selvapathy P. Removal of reactive dyes from wastewater by adsorption on coir pith activated carbon. Bioresour Technol. 2006;97(11):1329-36. [PubMed ID: 16040240]. https://doi.org/10.1016/j.biortech.2005.05.016.

  • 7.

    McKay G, Porter JF, Prasad GR. The removal of dye colours from aqueous solutions by adsorption on low-cost materials. Water Air Soil Pollut. 1999;114(3-4):423-38.

  • 8.

    Doğan M, Alkan M, Onganer Y. Adsorption of methylene blue from aqueous solution onto perlite. Water Air Soil Pollut. 2000;120(3-4):229-48.

  • 9.

    Bereket G, Aro AZ, ozel MZ. Removal of Pb(II), Cd(II), Cu(II), and Zn(II) from Aqueous Solutions by Adsorption on Bentonite. J Colloid Interface Sci. 1997;187(2):338-43. [PubMed ID: 9073406].

  • 10.

    Mohamed MM. Adsorption properties of ionic surfactants on molybdenum-modified silica gels. Colloids Surf A: Physicochem Eng Aspect. 1996;108(1):39-48.

  • 11.

    Mohan D, Singh KP, Singh G, Kumar K. Removal of dyes from wastewater using flyash, a low-cost adsorbent. Indust Eng chem Res. 2002;41(15):3688-95.

  • 12.

    Ho Y, McKay G. Sorption of dye from aqueous solution by peat. Chem Eng J. 1998;70(2):115-24.

  • 13.

    McKay G, Otterburn MS, Sweeney AG. Surface mass transfer processes during colour removal from effluent using silica. Water Res. 1981;15(3):327-31.

  • 14.

    Panuccio MR, Sorgona A, Rizzo M, Cacco G. Cadmium adsorption on vermiculite, zeolite and pumice: batch experimental studies. J Environ Manage. 2009;90(1):364-74. [PubMed ID: 18082309]. https://doi.org/10.1016/j.jenvman.2007.10.005.

  • 15.

    Kaplan Bekaroglu SS, Yigit NO, Karanfil T, Kitis M. The adsorptive removal of disinfection by-product precursors in a high-SUVA water using iron oxide-coated pumice and volcanic slag particles. J Hazard Mater. 2010;183(1-3):389-94. [PubMed ID: 20691538]. https://doi.org/10.1016/j.jhazmat.2010.07.037.

  • 16.

    Moraci N, Calabro PS. Heavy metals removal and hydraulic performance in zero-valent iron/pumice permeable reactive barriers. J Environ Manage. 2010;91(11):2336-41. [PubMed ID: 20643500]. https://doi.org/10.1016/j.jenvman.2010.06.019.

  • 17.

    Ozturk B, Yildirim Y. Investigation of sorption capacity of pumice for SO 2 capture. Process Safety Environ Protec. 2008;86(1):31-6.

  • 18.

    Yavuz Ö, Aydin AH. Removal of direct dyes from aqueous solution using various adsorbents. Polish J Environ Studies. 2006;15(1):155-61.

  • 19.

    Alkan M, Doğan M. Adsorption of copper (II) onto perlite. J Colloid Interface Sci. 2001;243(2):280-91.

  • 20.

    Han R, Wang Y, Han P, Shi J, Yang J, Lu Y. Removal of methylene blue from aqueous solution by chaff in batch mode. J Hazard Mater. 2006;137(1):550-7. [PubMed ID: 16600482]. https://doi.org/10.1016/j.jhazmat.2006.02.029.

  • 21.

    El Qada EN, Allen SJ, Walker GM. Adsorption of methylene blue onto activated carbon produced from steam activated bituminous coal: a study of equilibrium adsorption isotherm. Chem Eng J. 2006;124(1):103-10.

  • 22.

    Chen H, Zhao J, Dai G. Silkworm exuviae--a new non-conventional and low-cost adsorbent for removal of methylene blue from aqueous solutions. J Hazard Mater. 2011;186(2-3):1320-7. [PubMed ID: 21185648]. https://doi.org/10.1016/j.jhazmat.2010.12.006.

  • 23.

    Karagoz S, Tay T, Ucar S, Erdem M. Activated carbons from waste biomass by sulfuric acid activation and their use on methylene blue adsorption. Bioresour Technol. 2008;99(14):6214-22. [PubMed ID: 18207735]. https://doi.org/10.1016/j.biortech.2007.12.019.

  • 24.

    Hameed BH, Din AT, Ahmad AL. Adsorption of methylene blue onto bamboo-based activated carbon: kinetics and equilibrium studies. J Hazard Mater. 2007;141(3):819-25. [PubMed ID: 16956720]. https://doi.org/10.1016/j.jhazmat.2006.07.049.

  • 25.

    Rao GB, Kalyani G, Saradhi BV, Kumar YP. Removal of Fluoride from Aqueous Solution Using a Waste Material. Nature Environ Pollut Tech. 2009;8(2):231-6.

  • 26.

    Langmuir I. The adsorption of gases on plane surfaces of glass, mica and platinum. J American Chem Soc. 1918;40(9):1361-403.

  • 27.

    Abdelwahab O. Evaluation of the use of loofa activated carbons as potential adsorbents for aqueous solutions containing dye. Desal. 2008;222(1):357-67.

  • 28.

    Ng C, Losso JN, Marshall WE, Rao RM. Freundlich adsorption isotherms of agricultural by-product-based powdered activated carbons in a geosmin-water system. Bioresour Technol. 2002;85(2):131-5. [PubMed ID: 12227536].

  • 29.

    Akbal F. Adsorption of basic dyes from aqueous solution onto pumice powder. J Colloid Interface Sci. 2005;286(2):455-8. [PubMed ID: 15897057]. https://doi.org/10.1016/j.jcis.2005.01.036.

  • 30.

    Asgari G, Roshani B, Ghanizadeh G. The investigation of kinetic and isotherm of fluoride adsorption onto functionalize pumice stone. J Hazard Mater. 2012;217-218:123-32. [PubMed ID: 22476092]. https://doi.org/10.1016/j.jhazmat.2012.03.003.

  • 31.

    Mahvi AH, Heibati B, Mesdaghinia A, Yari AR. Fluoride Adsorption by Pumice from Aqueous Solutions. J Chem. 2012;9(4):1843-53.

  • 32.

    Veliev EV, Ozturk T, Veli S, Fatullayev AG. Application of diffusion model for adsorption of azo reactive dye on pumice. Polish J Environ Studies. 2006;15(2):347-53.

  • 33.

    Freundlich H. Über die adsorption in lösungen. Engelmann, Leipzig. 1906;57(A):385-470.

  • 34.

    Temkin MJ, Pyzhev V. Recent modifications to Langmuir isotherms. Acta Physiochim USSR. 1940;12:217-22.

  • 35.

    Dubinin MM, Zaverina ED, Radushkevich LV. Sorption and structure of active carbons. I. Adsorption of organic vapors. Zhurnal Fizicheskoi Khimii. 1947;21:1351-62.

  • 36.

    Rieman W, Walton H. Ion Exchange in Analytical Chemistry, International Series of Monographs in Analytical Chemistry. Pergamon Press, Oxford; 1970.

  • 37.

    Altenor S, Carene B, Emmanuel E, Lambert J, Ehrhardt JJ, Gaspard S. Adsorption studies of methylene blue and phenol onto vetiver roots activated carbon prepared by chemical activation. J Hazard Mater. 2009;165(1-3):1029-39. [PubMed ID: 19118948]. https://doi.org/10.1016/j.jhazmat.2008.10.133.

  • 38.

    Çolak F, Atar N, Olgun A. Biosorption of acidic dyes from aqueous solution by Paenibacillus macerans: Kinetic, thermodynamic and equilibrium studies. Chem Eng J. 2009;150(1):122-30.

  • 39.

    Murugan T, Ganapathi A, Valliappan R. Removal of dyes from aqueous solution by adsorption on biomass of mango (Mangifera indica) leaves. J Chem. 2010;7(3):669-76.

  • 40.

    Lagergren S. Zur theorie der sogenannten adsorption geloster stoffe. Kungliga Svenska Vetenskapsakademiens. Handlingar. 1898;24:1-39.

  • 41.

    Ahmad AA, Hameed BH, Aziz N. Adsorption of direct dye on palm ash: kinetic and equilibrium modeling. J Hazard Mater. 2007;141(1):70-6. [PubMed ID: 16887263]. https://doi.org/10.1016/j.jhazmat.2006.06.094.

  • 42.

    Ho Y, McKay G. Pseudo-second order model for sorption processes. Proc Biochem. 1999;34(5):451-65.

  • 43.

    Weber WJ, Morris JC. Kinetics of adsorption on carbon from solution. J Sanit Eng Div Am Soc Civ Eng. 1963;89(17):31-60.

  • 44.

    Mall ID, Srivastava VC, Agarwal NK. Removal of Orange-G and Methyl Violet dyes by adsorption onto bagasse fly ash—kinetic study and equilibrium isotherm analyses. Dyes Pigments. 2006;69(3):210-23.

  • 45.

    Amin NK. Removal of direct blue-106 dye from aqueous solution using new activated carbons developed from pomegranate peel: adsorption equilibrium and kinetics. J Hazard Mater. 2009;165(1-3):52-62. [PubMed ID: 18986765]. https://doi.org/10.1016/j.jhazmat.2008.09.067.