1. Background
The safety of all industries was examined by a group of continuous and systematic infrastructures, which are specified as “Critical Infrastructures” (1). These infrastructures can be systems, resources, a process, or a combination of these elements; the failure or unavailability of these infrastructures can interrupt the normal operation and safety of an industry (1). Maintenance procedures in complex industries are vulnerable to human performance (2, 3). Also, defects in human performance is one of the main reasons for accidents in maintenance operations of natural gas and oil industries. According to various studies in the context of human reliability, human error is the main cause of many accidents in various industries (4-7). For instance, more than 80% of failures in the chemical and petro-chemical industries (7) have been caused by human error. Therefore, it is required to analyze human reliability as well as system reliability. Over the years, various techniques have been developed for assessment of human reliability called human reliability analysis (HRA) methods. The HRA methods are a group of applicable tools for identification, modeling, qualification, and quantification of human error. Furthermore, HRA is a generic title for any method that estimates human error probability (HEP) for vital activities, to which human performance contributes (8). These methods are sometimes used to reduce human error in the context of probabilistic risk analysis (PRA) (9). At the moment, there are more than a dozen HRA methods for HEP in different systems, such as THERP (10), ASEP (11, 12), ATHEANA (13), SHERPA (14), CREAM (15), SPAR-H (16), and new methods are being developed. Today, various HRA methods have been utilized in multiple engineering applications (17-22). For example, Mandal et al. (18) identified probability of human error through overhead crane operation tasks using SHERPA methodology. Recently, Akyuz and Celik (19) applied a hybrid of HEART techniques and Interval type-2 fuzzy sets for assessment of human reliability for cargo operation.
Pipeline inspection gauge (PIG) operation, known as “pigging operation”, is one of the available maintenance activities for the inspection of oil and gas pipelines. Employing PIG devices are considered as a preventive maintenance procedure. Therefore, PIGs are applied for online monitoring of pipeline functionality in an operational condition. This online monitoring helps in taking corrective actions at the proper time and is useful for increasing the lifespan of pipelines (23). The most important identified risks in pigging process, such as high gas/liquid pressure in pipelines, excessive and uncontrolled speed of a PIG, the PIG striking equipment or operators and explosion, may lead to catastrophic accidents. Each year numerous incidents and accidents occur in the pigging process globally, some of which have been reported in the recent years. Table 1 describes some accidents in the current operation. These accidents are a small part of accidents that occur in pigging operations around the world. Although rigorous safety procedures are being applied in oil and gas industries, it seems that these procedures are not secure enough to prevent accidents and factors, such as human error, play a decisive role in these incidents.
Table 1.Examples of Accidents in the Pigging Operation
| Place (Location) | Year | Descriptions | Consequence |
|---|---|---|---|
| Iran, Zahedan (24) | February 6, 2017 | A pig device struck two operators. | Two workers were killed |
| Iran, Fars (25) | August 7, 2016 | In pressure decreasing procedure of receiver in pigging process of gas transmission pipeline an explosion happened. | Two workers with burns covering 90 percent and 45 percent of their bodies and one operator were killed by shock wave from the blast. |
| India, Telangana (26) | April 4, 2015 | The accident occurred when a PIG device, which is used to clean the pipeline, was ejected out of the pipeline. | At least two operators were burnt alive in a gas pipeline explosion, four other workers were also injured in the blast. |
| Nigeria (27) | March 13, 2015 | During an internal inspection project, two batch pigs were ejected under pressure from the barrel pig receiving trap. | PIG device struck two operators and two workers were seriously injured. |
In the present study, SPAR-H methodology and Bayesian Network (BN) were selected for analyzing human error. Although the SPARH technique was not originally developed for petrochemical industries, it has recently been applied for analysis of human reliability in risk assessment of a major accident in the Norwegian petroleum industry, offshore drilling operations in the oil and gas industry, and permit to work (PTW) system in a chemical plant (28-30).
A BN is a probabilistic graphic-based model that represents variables as nodes and also demonstrates the relationship between nodes using directed acyclic arcs. A BN employs a practical manner to utilize information and knowledge from various sources and handle missing data (31). The BN has been implemented in different contexts to estimate the probability of human error knowing that the model can conduct predictive analysis as well as diagnostic analysis. For instance, Islam et al. (3) applied BN for assessment of HEP during maintenance activities of marine systems. Musharraf et al. (32) applied BN during offshore emergency conditions.
2. Objectives
The main objective of the current study was to develop a SPAR-H- BN model to identify and analyze human errors in pigging operation in a gas transmission company. The application of the developed model assists the gas transmission company to analyze the probability of errors for pigging operation more accurately.
3. Methods
3.1. SPAR-H Methodology
In 1999, standardized plant analysis risk-human reliability (SPAR-H) was developed to succeed the accident sequence precursor (ASP) program (16, 33). Moreover, SPAR-H is the most practical technique that can be used by practitioners in any industry and this method calculates the likelihood of risks in post-initiator scenarios. The SPAR-H technique includes eight performance shaping factors (PSFs) that could influence human error probability (HEP), which is tabulated in Table 2 (34). There are two types of activity available in plant operation in the SPAR-H method: diagnosis and action. Moreover, for calculation of probability of human error, this methodology uses a dedicated multiplier for each PSF level and different formulas, according to negative levels of PSFs.
3.2. Fundamentals of Bayesian Networks (BN)
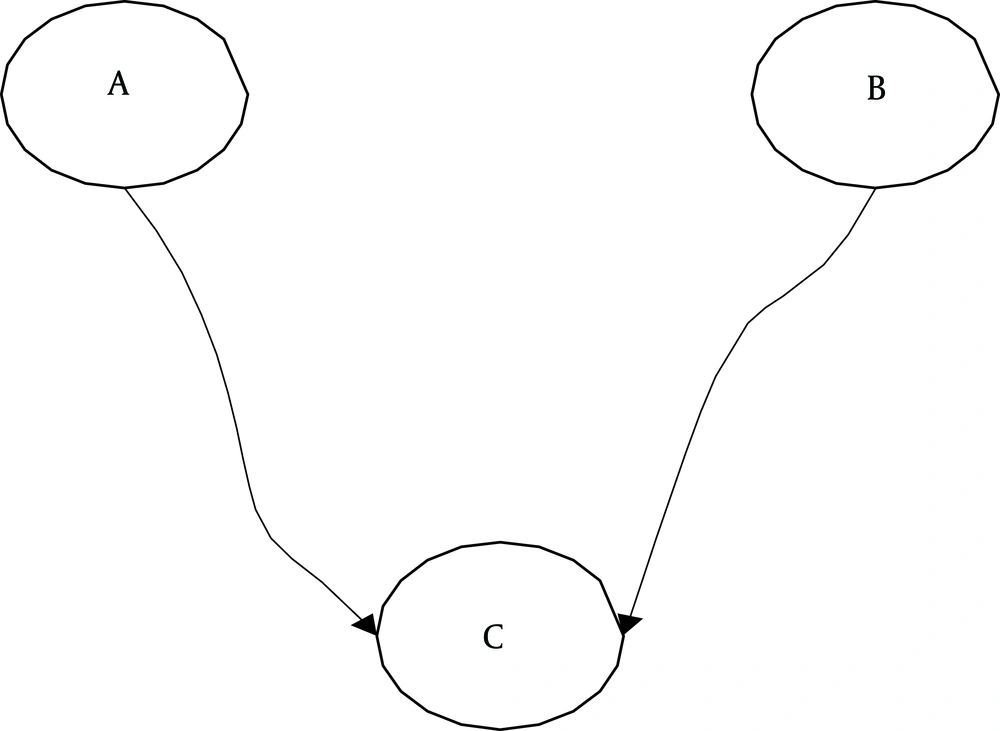
A BN is constituted from a group of unsystematic variables and their casual dependencies indicating probabilistic dependencies and interdependencies among variables through directed acyclic graph (DAG) (35). Besides that, BNs are developed from nodes and arcs (36). Nodes represent a random variable whereas probabilistic dependencies among variables are represented through arcs. Also, arcs directions show cause-effect dependencies among variables (37). A simple Bayesian network has been shown in Figure 1. Node C is a consequence or child node of A and B as parent nodes of C. Generally, in a BN, a node without any parent nodes and incoming arcs is called a “root node” and a node without child nodes and outgoing nodes is called a “leaf node” (38).
Figure 1.
A simple Bayesian network
The BNs are used to specify a joint probability distribution through variables and DAGs (39, 40). Root nodes have a marginal probability distribution (MPD), and all other connected nodes have conditional probability distributions (CPD), which are dependent on the root nodes. Furthermore, a CPD indicates the effect of parent nodes on child node using quantifying process (40). For representing the quantitative effects of discrete parent nodes on their child node, a conditional probability table (CPT) has been assigned to each parent node and in the same way for each discrete root node or each continuous root node, a prior probability table or a function has been defined, respectively (41). According to the chain rule, a BN explains the joint probability distribution over all the variables, which are available in the DAG and in the following estimates the marginal and the conditional probabilities for each node of the network (42). Therefore, chain rule determines joint probability distribution through encoding the BNs process between variables (38) and calculates entries in joint probability distribution on the basis of BNs information. Joint probability distribution P(U) of variable U is:
Where Пi is the parent set of variable Xi. Based on this, the marginal probability is calculated from the following equation:
In the present study, for assessment of HEP, a study group was organized consisting of a health and safety officer, resident supervisor (supervisor 1), gas transmission plant supervisor (supervisor 2), test-men operator, compressor operator, and researcher (as an interviewer). Note that all participated operators had more than four years of experience. In the first step, to capture the prior probabilities about PSFs levels, 45 questionnaires (SPAR-H worksheet) in pigging operation subtasks (three different pigging operations) were filled by experienced operators (experts). These prior probabilities were revised by gas transmission plant senior supervisor (with more than 15 years of experience). In the second step, researchers (as model builders) used prior probabilities to develop the final model. The process of developing the SPAR-H BN model is as follows:
3.3. Combine SPAR-H with Bayesian Network for Pigging Operation
When analyzing HFEs by the SPAR-H method, information and evidence of all PSFs are not available, thus, HRA practitioners have to deal with “insufficient information” for one or more PSFs in these cases. In SPAR-H method, value 1 is assigned to “insufficient information” level, which is the same as a “nominal” level value. This may lead to a HEP, similar to one that is calculated from cases with perfect evidence being generated. In fact, lack of evidence about some PSFs does not mean the evidence is at “nominal” level, which is one of the important issues in the SPAR-H method. Besides, BNs are beneficial for application of prior probabilities in conditions with “insufficient information”. In the present article, the SPAR-H BN model was developed using Agenarisk version 5.0.0 (43). The BN structure was constructed according to the SPAR-H methodology. The conditional probability table (CPT) was developed using expert judgment about performance shaping factors (PSFs) states in pigging operation. In this study, expert judgment has been incorporated with observational data and information contained in the literature (44) to capture the prior probability of each state of each PSF for action tasks. This information was used to extend marginal probability table (MPT) for the PSFs. The ultimate goal of SPAR-H BN model is estimation of MPT for the error node. Therefore, SPAR-H BN model used Equation 2 to capture marginal probability.
3.3.1. Arrangement of SPAR-H in a BN (Qualification Phase)
According to SPAR-H methodology, eight PSFs effect on the probability of error mathematically as in the following function:
Therefore, to construct a qualified model, two types of node were chosen: PSFs nodes and error node. In total, nine nodes exist: eight nodes of eight PSFs and one node of human error. Based on SPAR-H methodology instruction, PSFs in this method are independent and each of these PSFs directly effects on the probability of human error. Hence, arcs were used to demonstrate conditional independence among PSFs. Initial structure of SPAR-H BN is depicted in Figure 2. In the created model, the levels of each PSF were the same as each PSF level in the original SPAR-H methodology (except “insufficient information” level). The PSFs of SPAR-H method and their related levels and prior probabilities are listed in Table 2. The error node calculates human failure events probability based on PSFs nodes level and has two discrete levels: 1 (error occur = P (error)) and 0 (error not occur = 1 - P (error)). With regards to the original SPAR-H method, PSFs are independent so there is no casual arc between PSFs nodes and only the casual arcs exists between each PSF and error node.
Figure 2.
Naïve SPAR-H BN model for pigging process
3.3.2. Development of Conditional Probability Table (CPT)
3.3.2.1. CPT of PSFs Nodes
For development of CPT of each PSF node, the expert-elicited probabilities of PSFs levels in pigging operation were used. The probability values for each PSF level are listed in Table 2. Bayesian networks have the ability to use prior possibilities (40). In SPAR-H methodology, in some cases, information about PSFs levels are incomplete. This methodology assigned “insufficient information” level with multiplier of one for these cases, which is the same as assigning “nominal” level. However, lack of access to information about PSFs does not mean the PSFs are in “nominal” level. Besides, “insufficient information” level in SPAR-H methodology was excluded in order to use available prior probabilities in Table 2.
Table 2.SPAR-H Method PSFs, Their Related State, Multiplier, and Prior Probability of Each State
| PSF, State | Multiplier (Diagnosis Tasks) | Multiplier (Action Tasks) | Prior Probabilities (Action Tasks) |
|---|---|---|---|
| Available time | |||
| Time available ≥ 50 × the time required | 0.01 | 0.01 | 0.005 |
| Time available ≥ 5 × the time required | 0.1 | 0.1 | 0.15 |
| Nominal time | 1 | 1 | 0.80 |
| Time available is ~ the time required | 10 | 10 | 0.055 |
| Inadequate time | P (failure) = 1 | P (failure) = 1 | 0.000001 |
| Stress/stressors | |||
| Nominal | 1 | 1 | 70.1 |
| High | 2 | 2 | 17.7 |
| Extreme | 5 | 5 | 12.2 |
| Complexity | |||
| Clear diagnosis | 0.1 | - | - |
| Nominal | 1 | 1 | 58.5 |
| Moderately complex | 2 | 2 | 36.6 |
| Highly complex | 5 | 5 | 4.9 |
| Experience/training | |||
| High | 0.5 | 0.5 | 43.4 |
| Nominal | 1 | 1 | 56.1 |
| Low | 10 | 3 | 2.5 |
| Procedure | |||
| Nominal | 1 | 1 | 57.2 |
| Available, but poor | 5 | 5 | 30.6 |
| Incomplete | 20 | 20 | 9.7 |
| Not available | 50 | 50 | 2.5 |
| Ergonomics/human machine interference (HMI) | |||
| Good | 0.5 | 0.5 | 11.3 |
| Nominal | 1 | 1 | 44.1 |
| Poor | 10 | 10 | 41.3 |
| Missing/misleading | 50 | 50 | 3.3 |
| Fitness for duty | |||
| Nominal | 1 | 1 | 90.7 |
| Degrade fitness | 5 | 5 | 9.3 |
| Unfit | P (failure) = 1 | P (failure) = 1 | 0.000001 |
| Work processes | |||
| Good | 0.8 | 0.5 | 22.0 |
| Nominal | 1 | 1 | 74.7 |
| Poor | 5 | 5 | 3.3 |
3.3.2.2. CPT of an Error Node
The SPAR-H methodology estimates probability of human error using predefined expression based on PSF composite. The value of HEP depends on the PSFs levels (P (error | PSF1-8). Considering this, to develop a CPT the number of probabilities will increase exponentially according to the number of parent nodes (45). In a case, such as SPAR-H method with the eight parent node, the number of probabilities is more than a thousand. Therefore, to develop the CPT of the error node, simulation node and coding process were applied to build error node CPT more conveniently and more accurately. It follows that:
Agenarisk software benefits from a node probability table (NPT) editing mode, which makes it possible to use a mathematical expression to build a CPT of nodes. Given that to construct the error node CPT, the SPAR-H formula (which is mentioned in the next section explicitly) was coded in the model directly. In the event that the “available time” and “fitness for duty” levels are “inadequate” and “unfit” respectively, the probability of human error is appointed equivalent to 1 notwithstanding the other PSFs levels (like original SPAR-H methodology). Based on the original SPAR-H method instruction, this method uses a correction factor for three or more negative levels of PSFs so a dummy node was used for counting the negative nodes in the Agenarisk model. At the end, a coding was added for testing if estimated value of error exceeded 1.0, rounding down the value of error to 1.0.
3.3.3. Estimating the Probability of Human Error
The BN model of SPAR-H uses the marginal probabilities of CPT of PSF composite to estimate the probability of human error. It is found that:
In cases with complete information about PSFs states, the SPAR-H BN model estimates HEP the same as the original SPAR-H methodology yet in cases with insufficient information, the SPAR-H BN model uses prior probabilities to estimate HEP. It demonstrates the strength of this model to quantify human error. Figure 2 exhibits the SPAR-H BN model with no new information from pigging operation. This means no evidence entered the model (prior model).
3.4. Application of Developed Model: Identifying and Analyzing Human Errors Using the SPAR-H BN Model
This descriptive cross-sectional study was done to analyze human reliability in pipeline inspection gauge (PIG) operation in a gas transmission company in Iran. First, hierarchical task analysis (HTA) was conducted via a walk through in pigging operation and interviewing workers along with assessment procedures of various tasks in the studied company (Table 3). Accordingly, investigating human error probability (HEP) in PIG operation tasks/subtasks set was a goal of the present study. Afterwards, the BN model of SPAR-H (for action tasks) and SPAR-H (for diagnosis tasks) method (16) were utilized to estimate the probability of human error.
According to SPAR-H, step-by-step guidance (46), the following steps were done for human reliability analysis in PIG operation:
Step 1: Categorizing the HFE as Diagnosis and/or Action
In this step, PIG operation recognized HFEs, were classified as either diagnosis tasks or action tasks or both. For quantification purpose of SPAR-H method, diagnosis tasks represent the complete spectrum of cognitive processing and action tasks represent tasks that have been executed. According to Gertman et al.’s study (16), SPAR-H method dedicated nominal human error probability (NHEP) values of 0.01 and 0.001 for diagnosis tasks and action tasks, respectively. These values refer to error rate in cognitive processing for diagnosis tasks and also refer to error rate on simple action implementation, such as pressing a button or turning a dial, and simple slips or lapses for action tasks.
Step 2: Assessment and Rating Eight Performance Shaping Factors (PSFs)
The next step was to analyze HFEs in pigging operation based on eight PSFs in Table 2. Each PSF was investigated with respect to HFEs contexts. Therefore, numerical values were allocated according to SPAR-H instruction to each HFE. To achieve this goal, a series of interviews with experts and operators, who participated in PIG operation along with observation of work procedure, was done. Note that in the action tasks, when there was some doubt about choosing the appropriate PSF levels, the multiplier was shown by a question mark (Table 4) and then, the BN model of SPAR-H was used to estimate HEP. It should be noted in some subtasks of action tasks, some doubt existed with regards to rating PSFs. Therefore, in these cases, SPAR-H BN model was used to estimate HEP.
Step 3: Estimating PSF-Modified HEP
After the PSFs levels were determined, the PSF composite was estimated through multiplying these PSFs levels. Then, the final HEP was calculated by multiplying NHEP by the PSF composite (Equation 5).
For condition with three or more negative PSFs levels (levels with multiplier greater than 1), HEP was calculated using the correction factor, according to Equation 6:
Where HEP is human error probability, NHEP is nominal human error probability for diagnosis task and action task activity are 0.01 and 0.001, respectively. PSF is performance shaping factors multiplier.
It should be noted that the prior probability of states of PSFs, which have been mentioned in previous sections, is only for PSFs of action task, moreover, the prior probability of diagnosis tasks is being studied. Therefore, in this step, Bayesian model of SPAR-H methodology was used to estimate probability of human error for action tasks. Original SPAR-H methodology was used for estimation of probability of human error in diagnosis tasks, which means that in a condition with partial information (“insufficient information”), the SPAR-H BN model and original SPAR-H methodology were applied for action tasks and diagnosis tasks, respectively.
Step 4: Calculation of Independent HEP
For a single HFE with composed diagnosis and action tasks, two HEPs were determined separately and then summed to produce the composite HEP. Human error probability for independent tasks was calculated according to Equation 7:
Where PW/OD is human error probability (HEP) for Independent task, HEPA is human error probability (HEP) for action tasks, HEPD is human error probability (HEP) for diagnosis tasks.
Step 5: Accounting for Dependency
In the SPAR-H method, dependency between two tasks refers to the extent, to which performance on one task effects performance of a subsequent task (47). Dependency may be recognized between two tasks carried out by the same crew or among multiple tasks conducted by different operators (16). As a result, the HEP on one task increases the probability of human error on a subsequent task (47). Given the dependence of some tasks, dependency among tasks in the studied process is calculated from Table 4. Accordingly, there were five types of dependency (complete, high, moderate, low, and zero) among tasks that were determined according to crew (same or different), time (close in time or not close in time), location (same or different), and cause (additional or not additional).
Table 3.Hierarchical Task Analysis (HTA) of Tasks in Pigging Operation
| Operator | Task | Sub Task (Symbol) |
|---|---|---|
| Supervisor | Checking the gas flow rate in the pipeline | Estimation of the average flow rate of the pipeline (X1) |
| Calculation of gas velocity based on gas flow rate (X2) | ||
| Calculation of the required average gas velocity for crossing the pig (X3) | ||
| Comparison of the average gas flow rate in the pipeline and the required average velocity for PIG crossing (X4) | ||
| Ensuring the PIG dimensions | Controlling the changes in a pig that had been used previously (X5) | |
| Comparing the diameter of the PIG with the barrel-shaped section of pipeline and trap (X6) | ||
| Ensuring the openness of the valves in lines | Paying attention to the relief valve gauge (X7) | |
| Checking valves manually (X8) | ||
| Issuing permit to work | Handover the work to the operators (X9) | |
| Signing the permit (X10) | ||
| Validation & revalidation after shift handover (X11) | ||
| Compressor operator and semi-skilled worker | Injection of air to the back of PIG | Connecting the hose to the pipeline (X12) |
| Turning on the compressor (X13) | ||
| Enhancing the pressure (X14) | ||
| Pressure decreasing (X15) | ||
| Turning off the compressor (X16) | ||
| Test man | PIG launching | Importing the PIG to header and pipeline (X17) |
| Closing the header (X18) | ||
| Activation of PIG signaler (X19) | ||
| Checking vent and drain valves (X20) | ||
| Opening the kicker valve for enhancing pressure (X21) | ||
| Checking pressure gauges (X22) | ||
| PIG receiving | Opening bypass valve for decreasing pressure (X23) | |
| Opening drain and vent valve for evacuation of pipeline (X24) | ||
| Checking pressure gauges and ensuring full discharge of pressure in pipeline (X25) | ||
| Taking of the pig (X26) | ||
| Cleaning the garbage that remains from pigging operation for fire and explosion prevention (X27) |
Table 4.An Example of the SPAR-H Worksheet for Dependency Determination in “Opening the Kicker Valve for Enhancing Pressure” Task
| Condition Number | Crew (Same or Different) | Time (Close in Time or not Close in Time) | Location (Same or Different) | Cause (Additional or not Additional) | Dependency | HEP Calculation Formula |
|---|---|---|---|---|---|---|
| 1 | S | c | s | na | complete | For complete dependence the probability of failure is 1 |
| 2 | a | complete | ||||
| 3 | d | na | high | For high dependence the probability of failure is (1 + Pw/od)/2 | ||
| 4 | a | high | ||||
| 5 | nc | s | na | high | ||
| 6 | a | moderate | For moderate dependence the probability of failure is (1 + 6 × Pw/od)/7 | |||
| 7 | d | na | moderate | |||
| 8 | a | low | For low dependence the probability of failure is (1 + 19 × Pw/od)/20 | |||
| 9 | D | c | s | na | moderate | For moderate dependence the probability of failure is (1 + 6 × Pw/od)/7 |
| 10 | a | moderate | ||||
| 11 | d | na | moderate | |||
| 12 | a | moderate | ||||
| 13 | nc | s | na | low | For low dependence the probability of failure is (1+19 × Pw/od)/20 | |
| 14 | a | low | ||||
| 15 | d | na | low | |||
| 16 | a | low | ||||
| 17 | zero | For zero dependence the probability of failure is Pw/od |
Table 5.Rating of PSFs and Estimation of HEPA and HEPD in Pigging Operation Tasks in the Studied Gas Transmission Plant
| Task/sub task | Operator | Diagnosis or Action or Both | PSF | HEP | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Available Time | Stress/Stressors | Complexity | Experience/ Training | Procedure | Ergonomics | Fitness for Duty | Work Processes | HEPA | HEPD | |||
| X1 | Supervisor 1 | D | 1 | 1 | 2 | 1 | 5 | 1 | 1 | 1 | - | 0.1 |
| X2 | Supervisor 1 | D | 1 | 1 | 2 | 1 | 5 | 1 | 1 | 1 | - | 0.1 |
| X3 | Supervisor 1 | D | 1 | 1 | 2 | 1 | 5 | 1 | 1 | 1 | - | 0.1 |
| X4 | Supervisor 1 | D | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.01 | |
| X5 | Supervisor 1 | D | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | - | 0.01 |
| X6 | Supervisor 1 | D | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | - | 0.01 |
| X7 | Supervisor 1 | D | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | - | 0.01 |
| X8 | Supervisor 1 | A | 1 | 1 | 1 | 1 | (?,?,0,0) | 1 | 1 | 1 | 0.0023941 | - |
| X9 | Supervisor 2 | D | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | - | 0.02 |
| X10 | Supervisor 2 | D | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | - | 0.01 |
| X11 | Supervisor 2 | D | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | - | 0.01 |
| X12 | Compressor operator | A | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.001 | - |
| X13 | Compressor operator | A | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 0.002 | - |
| X14 | Compressor operator | A | 1 | 5 | 1 | 1 | (?,?,0,0) | 1 | 1 | 1 | 0.01197 | - |
| X15 | Compressor operator | A | 1 | 1 | 1 | 1 | (?,?,0,0) | 1 | 1 | 1 | 0.0023941 | - |
| X16 | Compressor operator | A | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.001 | - |
| X17 | Test man 1 | A | 1 | 2 | 2 | 1 | 1 | 10 | 1 | 1 | 0.038499 | - |
| X18 | Test man 1 | A | 1 | 1 | 1 | 1 | (?,?,0,0) | 10 | 1 | 1 | 0.023941 | - |
| X19 | Test man 1 | A | 1 | 1 | 1 | 1 | (?,?,0,0) | 1 | 1 | 1 | 0.0023941 | - |
| X20 | Test man 1 | D | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | - | 0.01 |
| X21 | Test man 1 | A | (0,0,?,?,0) | 5 | 2 | 1 | (?,?,0,0) | 10 | 1 | 1 | 0.20389 | - |
| X22 | Test man 1 | D | 1 | 1 | 1 | 1 | 0.5 | 1 | 1 | 1 | 0.005 | |
| X23 | Test man 2 | A | (0,0,?,?,0) | 5 | 2 | 1 | (?,?,0,0) | 10 | 1 | 1 | 0.20389 | - |
| X24 | Test man 2 | A | 1 | 2 | 2 | 1 | (?,?,0,0) | 10 | 1 | 1 | 0.083216 | - |
| X25 | Test man 2 | D | 1 | 2 | 2 | 1 | 0.5 | 1 | 1 | 1 | 0.02 | - |
| X26 | Test man 2 | A | 1 | 5 | (?,?,0) | 1 | (?,?,0,0) | 10 | 1 | 1 | 0.1305 | - |
| X27 | Test man 2 | A | 1 | 2 | 1 | 1 | (?,?,0,0) | 10 | 1 | 1 | 0.044742 | - |
4. Results
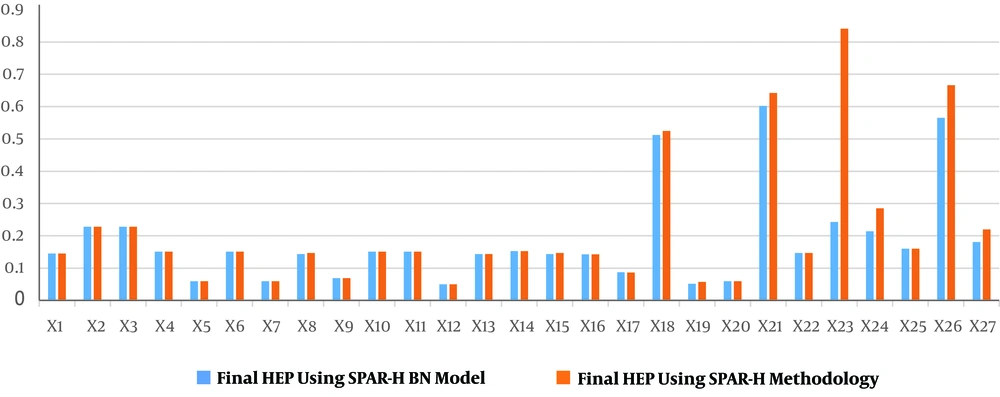
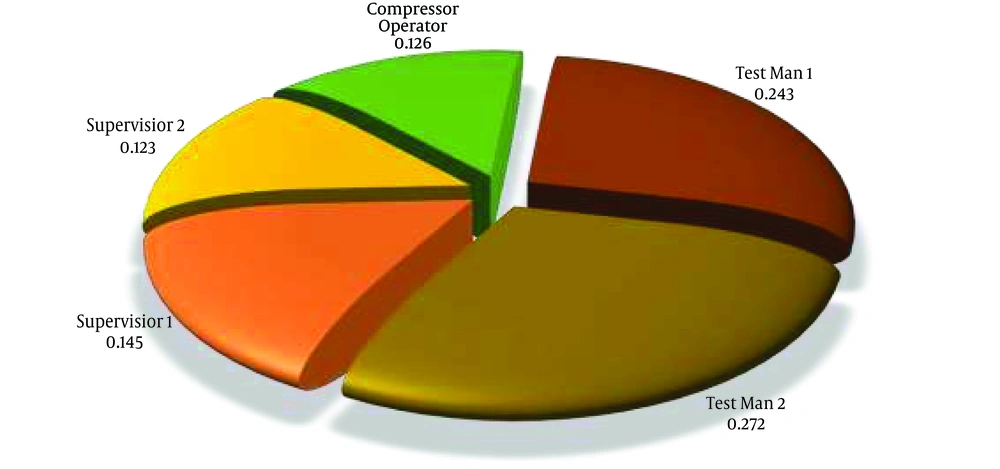
Application of the BN model of SPAR-H to the pigging operation is summed up in Figures 3 and 4. In total, five operators participated in pigging operation in the studied gas transmission company, and human reliability analysis was conducted for all tasks that were done in this operation. These operators included two supervisors (with seven and four years work experience, respectively). One compressor operator (with six years’ work experience) and two test-men (with eight and four years of work experience). Tasks and subtasks as a result of HTA are tabulated in Table 3. As the table illustrates, the pigging operation is comprised of seven tasks and also 27 subtasks. Table 5 presents the results of evaluation of each of the eight PSFs with regards to the context of subtasks, including diagnosis, action or both, along with the participated operators and HEPA or HEPD for all of them. Table 6 presents the values of HEPA, HEPD, PW/OD, PW/OD, the level of dependency, and final HEP for each subtask in pigging operation. According to the developed model outputs, the mean of final HEP in the studied pigging operation was 0.1724. The highest and the lowest final HEP was relevant to “opening the kicker valve for enhancing pressure” and “connecting the hose to the pipeline”, with values of 0.602 and 0.05, respectively. Figure 3 presents the comparison of final HEP among pigging operation tasks, and comparison of the final HEP in occupational groups that participated in pigging operation has been illustrated in Figure 4. These figures show the considerable differences between probabilities of human error in “test-man” operators with mean HEP.
Figure 3.
Comparison of the mean human error probability among tasks of pigging operation
Figure 4.
The mean probability of human errors in the operators involved in pigging operation in the studied gas transmission company
Table 6.Final Human Error Probabilities in Pigging Operation Tasks
| Task/Sub Task | Operator | HEPD | HEPA | PW/OD | Dependency | PW/D | Final HEP Using SPAR-H BN Model | Final HEP Using SPAR-H Methodology |
|---|---|---|---|---|---|---|---|---|
| X1 | Supervisor 1 | - | 0. 1 | 0.1 | Low | 0.145 | 0.145 | 0.145 |
| X2 | Supervisor 1 | - | 0. 1 | 0.1 | Moderate | 0.228 | 0.228 | 0.228 |
| X3 | Supervisor 1 | - | 0. 1 | 0.1 | Moderate | 0.228 | 0.228 | 0.228 |
| X4 | Supervisor 1 | 0.01 | 0.01 | Moderate | 0.151 | 0.151 | 0.151 | |
| X5 | Supervisor 1 | - | 0.01 | 0.01 | Low | 0.059 | 0.059 | 0.059 |
| X6 | Supervisor 1 | - | 0.01 | 0.01 | Moderate | 0.151 | 0.151 | 0.151 |
| X7 | Supervisor 1 | - | 0.01 | 0.01 | Low | 0.059 | 0.059 | 0.059 |
| X8 | Supervisor 1 | 0.0024 | - | 0.0024 | Moderate | 0.144 | 0.144 | 0.1471 |
| X9 | Supervisor 2 | - | 0.02 | 0.02 | Low | 0.069 | 0.069 | 0.069 |
| X10 | Supervisor 2 | - | 0.01 | 0.01 | Moderate | 0.059 | 0.151 | 0.151 |
| X11 | Supervisor 2 | - | 0.01 | 0.01 | Moderate | 0.059 | 0.151 | 0.151 |
| X12 | Compressor operator | 0.001 | - | 0.001 | Low | 0.050 | 0.050 | 0.050 |
| X13 | Compressor operator | 0.002 | - | 0.002 | Moderate | 0.144 | 0.144 | 0.144 |
| X14 | Compressor operator | 0.012 | - | 0.012 | Moderate | 0.153 | 0.153 | 0.153 |
| X15 | Compressor operator | 0.0024 | - | 0.0024 | Moderate | 0.144 | 0.144 | 0.147 |
| X16 | Compressor operator | 0.001 | - | 0.001 | Moderate | 0.143 | 0.143 | 0.143 |
| X17 | Test man 1 | 0.039 | - | 0.039 | Low | 0.087 | 0.087 | 0.0865 |
| X18 | Test man 1 | 0.024 | - | 0.024 | High | 0.512 | 0.512 | 0.525 |
| X19 | Test man 1 | 0.0024 | - | 0.0024 | Low | 0.052 | 0.052 | 0.0574 |
| X20 | Test man 1 | - | 0.01 | 0.01 | Moderate | 0.059 | 0.059 | 0.059 |
| X21 | Test man 1 | 0.204 | - | 0.204 | High | 0.602 | 0.602 | 0.642 |
| X22 | Test man 1 | 0.005 | 0.005 | Moderate | 0.147 | 0.147 | 0.147 | |
| X23 | Test man 2 | 0.204 | - | 0.204 | Low | 0.243 | 0.243 | 0.841 |
| X24 | Test man 2 | 0.084 | - | 0.084 | Moderate | 0.214 | 0.214 | 0.285 |
| X25 | Test man 2 | 0.02 | - | 0.02 | Moderate | 0.160 | 0.160 | 0.160 |
| X26 | Test man 2 | 0.13 | - | 0.13 | High | 0.565 | 0.565 | 0.666 |
| X27 | Test man 2 | 0.045 | - | 0.045 | Moderate | 0.181 | 0.181 | 0.220 |
| Average | - | - | - | - | - | - | 0.184 | 0.217 |
5. Discussion
The current study was performed in order to model SPAR-H methodology in BN in the context of pigging operation and also to characterize HFEs along with determining HEP in PIG operation in a gas transmission company through implementation of SPAR-H BN model and original SPAR-H methodology for action tasks and diagnosis tasks, respectively. First, SPAR-H methodology was modeled using BN and expert-elicited probabilities. In the second stage, for analyzing human error, firstly, a hierarchical task analysis was performed. In a total of seven main tasks and also twenty-seven subtasks were recognized in the studied company. According to the final HEPs in Table 6, HEP intervals for pigging operation were in the range of 0.05 and 0.602 and also the mean probability of human error in pigging operation was 0.184. Furthermore, the highest probability of human error was related to “opening the kicker valve for enhancing pressure” subtask (0.602), which may increase the risk of launcher rupture or hose rupture of pressure compressor and as a result increases the risk of exposure to high pressure of gas/liquid (400 - 1200 PSI) and operator mortality. This error is due to high dependency on the previous task, no availability of time (doubt exists), extreme stress level, moderate complexity in subtask, poor ergonomic condition, and also lack of (doubt exists) applicable procedure. The “taking of the pig” subtask also had high HEP value (0.565), which is due to probability of PIG device being struck in pipeline and also risk of PIG device striking the operator that can lead to extreme stress level. Furthermore, task complexity (doubt existed between levels), poor ergonomic condition, lack of a strong procedure (doubt existed between levels), and high dependency on the previous subtask made it a critical subtask. The “closing the header” subtask was another critical subtask in pigging operation (0.512). This error can lead to the launcher header staying open and cause the operator to be exposed to high pressure (gas/liquid). “Calculation of gas velocity based on gas flow rate” and “calculation of the required average gas velocity for crossing the pig” subtasks also had HEP (0.228) higher than mean HEP. Error in these subtasks can have catastrophic consequences, such as pipeline rupture (also launcher/receiver), explosion or jet fire. Moreover, X23, X24, and X27 subtasks have the high HEP value, which are due to poor ergonomic condition, no availability of strong procedure (doubt exists) and high stress level. Given the above, the mean HEP value in present study was 0.184, which was close to HEP value in the “sweep the line by pigging in order to drain all cargo residues” sub task (0.186) in Akyuz and Celik’s (48) study. In the current study, 37% of subtasks had high or extreme stress level and 50% of these cases with stress had complexity. This shows high correlation between these PSFs, which is in agreement with Abreu et al.’s study (21).
Given Figures 3 and 4, the subtasks that have been done by test man operators had the highest probability of human error. Because of the high interaction of “test-man” operators by pigging operation, they are faced with more stressful conditions, more complex tasks, and awkward ergonomics conditions. Supervising operators had a vital role in the pigging operation yet because of appropriate level of PSFs (the nominal level of stress, nominal ergonomic condition, etc.), the HEP values were lower than mean HEP. However, in some supervisor subtasks, the complexity was high and also the procedure was poor.
According to Peterson’s (49) study, human errors caused by weakness in the procedures are responsible for 24% of industrial accidents. Furthermore, using improper procedures can lead to rule-based human error (50). As mentioned above, the available procedures in pigging operation are not applicable and strong, which has a considerable effect on probability of human error. Therefore, by revising the procedures the HEP values can be decreased.
5.1. Evaluation of the Final Model
Based on models purpose, different evaluation methods are available. If the model was developed to carry out inference, the evaluation process of the model can be done via stakeholders or expert panel opinion (51). If the model (the BN model) has a target node, a sensitivity analysis can be used to determine the effect of sensitivity nodes (parent nodes) on the target node (child node) (52).
5.2. Sensitivity Analysis
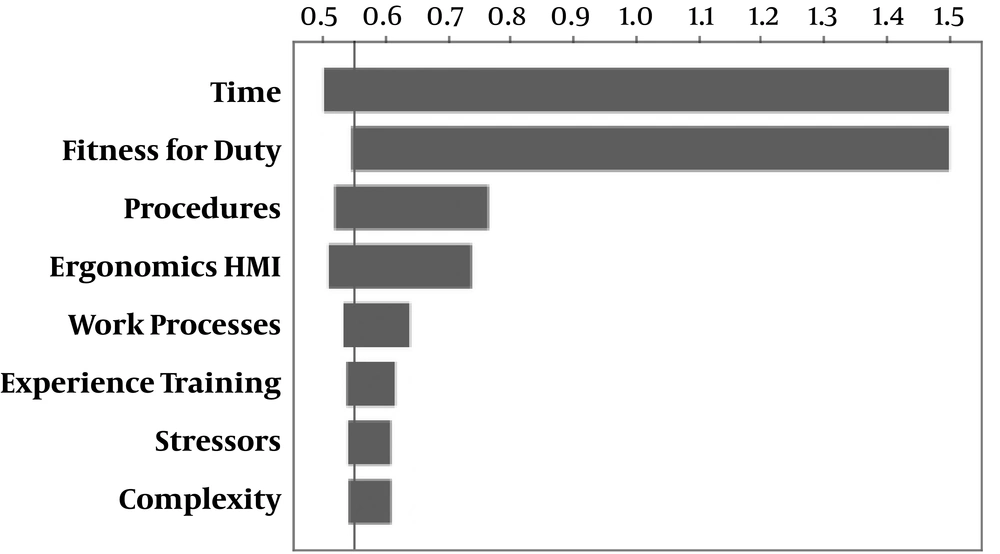
One of the most used features to validate BN models is sensitivity analysis. Therefore, in the present study, it was applied to test the developed model. Figure 5 illustrated the tornado graph for excepted values of error probability, which is resulted from the sensitivity analysis of the final model. According to tornado graph, the estimated final HEP are sensitive yet did not show abrupt changes to any minor change of the levels associated with the PSFs, except for levels of two PSFs (“time = not available” and “fitness for duty = unfit”, for these two level final HEP estimated equivalent to 1). Nevertheless, these changes are in accordance with the SPAR-H methodology completely. Therefore, sensitivity analysis approved the logically of the final model.
Figure 5.
Tornado graph for excepted values of error probability
5.3. Expert Judgment
As discussed at the end paragraph of section 2.2, in the present article, a study group (an expert panel) was organized consisting of a health and safety officer, resident supervisor (supervisor 1), gas transmission plant supervisor (supervisor 2), test-men operator, compressor operator, and researcher (as an interviewer). After initial evaluation about PSFs levels, experts panel were requested to judge the final probability of human error in the action tasks. The results of expert judgment were in convergent with output results of the developed model (correlation value = 0.73). Hence, the logically of the final model was authorized by expert judgment.
5.4. Comparison of SPAR-H BN Model with SPAR-H Methodology
In Figure 3, results of final human errors were compared. According to the comparison of output values from both SPAR-H BN model and SPAR-H methodology, which are presented in Table 6, although the HEPs of diagnosis task (subtask X1 to X11) are equal (because SPAR-H BN model is developed for action tasks), the main difference between the two methods can be seen in action tasks (X12 to X27). It was found that due to more accurate calculation of HEP in SPAR-H BN model than SPAR-H methodology, outputs of SPAR-H BN model are more realistic and are lesser than SPAR-H methodology outputs. For instance, for “opening bypass valve for decreasing pressure” subtask the output of SPAR-H BN model and SPAR-H methodology was 0.243 and 0.841, respectively. This means that in these cases, SPAR-H methodology estimates HEP very pessimistically, also this problem can be seen in X18, X19, X21, X24, X26, and X27. Pessimistic calculation of HEP increases the costs of industry and also enhances the stresses in managerial level. In addition, SPAR-H BN model prevents pigging operation practitioners from the optimistic calculation of HEP. This can lead to a lack of attention to the system or human performance deficiencies.
5.5. Conclusions
The SPAR-H method demonstrates an acceptable spectrum of factors influencing human performance in assessment of industries operations through a framework of an acceptable number of PSFs. This method is easy to use, simple, and a useful tool for practitioners to utilize for calculating HEP. Even though some deficiencies exist in this methodology, through implementing SPAR-H in BNs, some of the issues were addressed. The BNs were helpful to adapt the SPAR-H methodology to the pigging operation using dedicated prior probabilities. One of the main advantages of the presented SPAR-H model in this study was that once doubt existed for choosing PSFs states, the prior probabilities were used to estimate HEP accurately. Therefore, the probabilities of human error can be updated taking into account the more realistic operational and environmental conditions, such that SAPR-H methodology did not benefit from these advantages. In total, SPAR-H BN is a practical model for managers to understand working condition more realistically than SPAR-H methodology to decrease risks contributed with human performance.
