1. Background
The potential for thorough and precise evaluations has increased dramatically with the introduction and broad use of advanced imaging tools in dentistry. Although there are drawbacks to traditional two-dimensional imaging, advanced techniques like magnetic resonance imaging (MRI), computed tomography (CT), and cone-beam computed tomography (CBCT) offer high-resolution, multi-planar views in sagittal, coronal, and axial sections, enabling accurate quantification of linear, areal, and volumetric parameters (1, 2). Volumetric analysis is now an indispensable tool in modern dental practice, with applications across a wide range of clinical domains. Cone-beam computed tomography-based volumetric assessments allow clinicians to evaluate maxillofacial pathologies, periodontal defects, bone loss from periapical lesions, changes before and after orthognathic surgery, implant planning, graft monitoring, paranasal sinus evaluation, and airway space assessment. These volumetric evaluations provide detailed information regarding lesion characterization, treatment planning, and post-treatment monitoring (3-7).
Stereology has drawn attention among the many methods for volumetric calculations because of its mathematical rigor and proven reliability. Stereology is a field that derives three-dimensional information from two-dimensional images, allowing for robust estimation of the structural characteristics of complex biological objects (8, 9). Its core strengths lie in mathematical accuracy, objectivity, and a strong theoretical foundation (10, 11). Notably, stereological methods routinely yield unbiased and precise volumetric measurements (11, 12). The Cavalieri principle, a foundational stereological technique, is particularly valued for its effectiveness in volume estimation. By minimizing bias, it is especially suitable for evaluating irregular or complex structures — an area where conventional two-dimensional methods often fall short (13-15). According to this principle, the target structure is sliced at regular intervals, and the area of each cross-section is determined. The total volume is then calculated as the sum of the areas multiplied by the section thickness (16-22).
The following is a mathematical expression for the Cavalieri principle (9, 16):
Where V is the total volume of the structure, Ai is the area of each representative cross-section i, and t is the average section thickness. The total volume is obtained by summing the contributions of all slices:
Volume total = V1 + V2 + ⋯ + Vn
Finding the area of the projections or pictures inside each segment of the region of interest is the first step in applying the Cavalieri principle (11, 21). Planimetry and point-counting are two primary methods which commonly used to study this field (16, 22, 23). Planimetry often involves digital image analysis tools that either manually or automatically delineate structure boundaries on each image (11, 22-24). The point-counting method, on the other hand, uses a regularly spaced grid superimposed on each section (11, 15, 25). Each grid point marked (typically with a "+") represents a unit area
Where (∑Pi) represents the total number of grid points falling within the structure of interest.
This approach provides an unbiased estimate of the section area by multiplying the unit area per point by the total number of intersecting points (8, 9, 11, 16). The total volume (V) is then calculated by summing the area estimates for all sections and multiplying by the section thickness (t):
Despite the widespread use of CBCT in dental volumetric analysis, the combined influence of section orientation and slice interval on volume estimation using stereological techniques remains insufficiently studied (15, 16). This study addresses this important gap by systematically evaluating how these parameters influence volumetric calculations across multiple section orientations (axial, sagittal, and coronal) and slice intervals. The results could inform the development of standardized CBCT protocols and contribute to enhanced accuracy and reproducibility in clinical diagnoses. Archimedes’ principle is well-established as the gold standard for assessing volumetric accuracy in experimental settings. However, the specific effects of section orientation and slice interval on CBCT-based volumetric measurements under clinical conditions remain underexplored. This study directly addresses these factors by comparing stereological volume estimates across orientations and slice intervals. Our aim is to enhance both the accuracy and efficiency of volumetric assessments, thus supporting their broader implementation in routine dental practice.
2. Objectives
The objective of this study was to evaluate the volumetric accuracy of two CBCT-based measurement techniques — point-counting and planimetry — under varying section orientations and slice intervals. The results were compared with those obtained using Archimedes’ principle, which served as the reference standard.
3. Materials and Methods
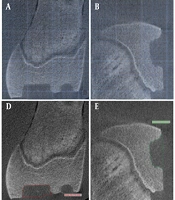
This study was approved by the Experimental Animals Local Ethics Committee, Bezmialem University, Turkey (2019/109). The study was conducted at the Department of Oral, Dental, and Maxillofacial Radiology, Istanbul University Faculty of Dentistry. Based on a power analysis with parameters α = 0.05, 1-β = 0.80, f (α,β) = 7.85, SD = 0.03, and effect size (μ₁ − μ₂) = 0.02, the required sample size was calculated to be 35,325. This theoretical value approximates 35 practical samples; thus, 35 defects were included in the study. Literature reports indicate that bovine bone from 2 - 3-year-old animals approximates human jawbone properties, particularly regarding trabecular density and cortical thickness. In contrast, metaphyseal and diaphyseal bone regions are considered unsuitable due to differences in mineralization and biomechanical properties (18). Therefore, epiphyseal regions of 2 - 3-year-old bovine femurs were used. Specimens not meeting these inclusion criteria were excluded. Seven bovine femoral bones were used to create 35 intraosseous defects. The defects were formed behind cap-shaped molds affixed to the femoral condyles and were purposefully made irregular in shape and depth to simulate the complexity of jawbone pathologies. A single experienced radiologist created all defects using tungsten carbide burs under standardized conditions to minimize intra-operator variability (Figure 1).
The defects were scanned using a Scanora® 3D-X CBCT unit (Soredex, Tuusula, Finland). The bones were embedded in water-filled plexiglass containers to simulate soft tissue and prevent movement during imaging. Imaging parameters included: 90 kV, 10 mA, a focal spot size of 0.5 mm, a target angle of 15°, and an exposure time of 24 seconds. High-resolution scanning was performed with a field of view (FOV) of 140 × 160 mm and a voxel size of 0.2 mm³. Section thickness was 0.2 mm, and the study assessed slice intervals of 6, 8, 10, 12, 16, and 20 slices. These values were selected based on clinical practice, where 1 mm intervals are commonly used but may be reduced for detailed assessments (17). No additional artifact-reduction algorithms were applied to preserve the standard clinical imaging environment. Images with significant artifacts or low diagnostic quality were excluded upon visual inspection by an experienced radiologist.
In this study, a radiologist with twenty years of experience prepared the defects and performed the Archimedes' evaluation, which was determined as the gold standard. For the radiologic examination, a separate examiner was deemed sufficient for the measurements, as the Cavalieri method is considered objective (19, 20). The volume measurements were performed by an oral and maxillofacial radiologist with four years of experience using the specified software to estimate the volume of bone defects. To evaluate intra-observer reliability, this examiner repeated every measurement after a 1-month interval. Kostec (Gangwon, South Korea) used an Advantech KT-R240FEE medical LCD display to evaluate the CBCT pictures.
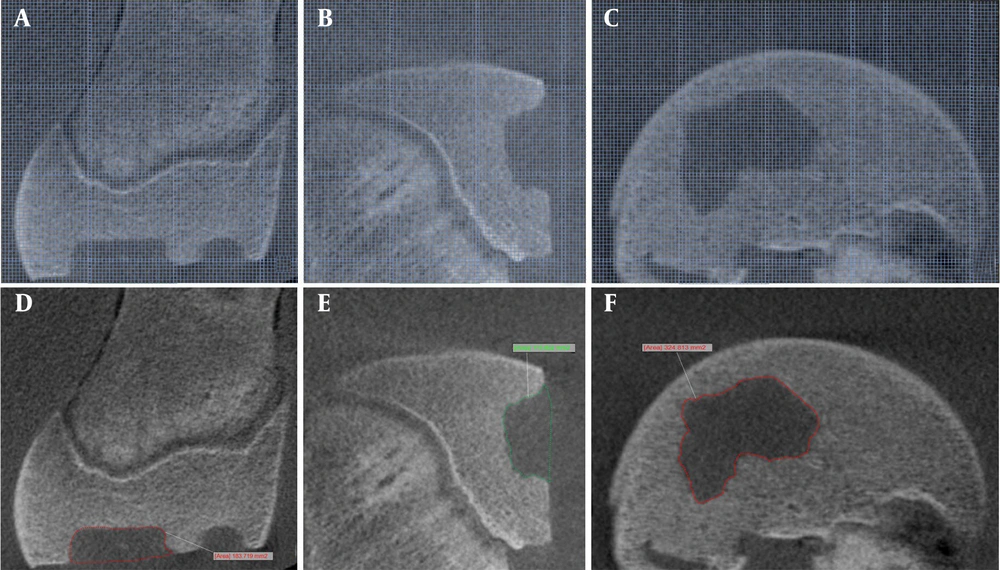
Cavalieri's concept was used to compute the volumes of the intraosseous defects using both the planimetry and point counting techniques. Image J (National Institutes of Health, Bethesda, USA) and OnDemand 3D TM software (Cybermed, California, USA) were used to carry out these computations. Three orthogonal sections were used to determine the sectional areas of all flaws using the planimetry and point counting techniques. Defect boundaries were manually defined using the OnDemand 3D TM software (Cybermed, California, USA) in the planimetry technique (Figure 2). The software automatically calculated the area after the defects' borders were determined. A constant slice thickness of 0.2 mm was used, and analyses were repeated at slice-intervals corresponding to 6 - 20 images. For each interval, the cumulative sectional area was multiplied by the slice thickness and by the number of intervals to yield the final volume.
"The ImageJ program from the National Institutes of Health (Bethesda, USA) was used to perform the point-counting method. This method involved calculating the area that corresponded to the number of points in each segment that intersected with the defect (Figure 2). During this procedure, a minimal area of 1.57 mm² was determined for each location. The software's point-counting ruler allows for the visual distinction of individual points, facilitated by this specific value. For each defect, an average of 80 to 120 points were selected, in accordance with Gunderson’s recommendation. To calculate the final volume, the entire area was multiplied by the sum of the slice thickness and the interval count Following the completion of the volume measurements using CBCT images, Archimedes' principle was applied to quantify the real volume of the defects. This approach, recognized as the gold standard, was the primary method used in our study to obtain accurate volume measurements. A silicone-based imprint material (Coltene® Speedex Light Body, Switzerland) was employed to ensure that each defect was fully filled. Before the polymerization of the impression material was completed, a pre-made cover was placed to prevent any gaps. The silicone imprint material was successfully polymerized, and the resulting impression was carefully removed from the model defectThe volumes of the measurement items removed from the defects were determined using a 50 ml pycnometer and a high-precision scale. The scale, provided by KERN & Sohn GmbH (Balingen, Germany), had a measuring accuracy of 0.0001 grams. To estimate the actual volume of internal voids or defects within the test samples, Archimedes’ principle was applied using a pycnometric method. The procedure involved three separate weight measurements:
Wpyc + water: The weight of the pycnometer completely filled with distilled water,
Wmat: The weight of the dried measurement sample, and
Wmat + pyc + water: The weight of the pycnometer after the sample was placed inside and displaced the excess water.
The real volume of the defect (V) was calculated based on the volume of water displaced by the sample using the following equation:
ρwater denotes the density of pure water (taken as 1.00 g/cm³ at 25°C). This method provides an accurate and reproducible estimate of the internal volume by comparing mass differences caused by water displacement.
All measurements were performed at room temperature, and each measurement was repeated three times to ensure reliability.
3.1. Statistical Analysis
SPSS 25.00 (IBM Corp. Released 2017. IBM SPSS Statistics for Windows, version 25.0. Armonk, NY: IBM Corp.) was used for statistical analysis. The Kolmogorov-Smirnov test was used to determine whether continuous variables were normal. The Mann-Whitney U test was used to compare the real volumes with those determined using radiographic methods, as the data did not follow a normal distribution. Descriptive statistics, including the mean, standard deviation, minimum, and maximum values, were calculated for continuous variables. A 95% confidence interval was maintained throughout the investigation, and a threshold of P < 0.05 was considered statistically significant. The intra-rater reliability of the observer in this study was assessed using the intraclass correlation coefficient (ICC). The agreement between Archimedes' data and both section orientation and slice intervals was evaluated using ICC analysis. A two-way random model with absolute agreement was applied. No missing data were present. Outlier analysis was performed using the interquartile range (IQR) method. A small number of outliers, primarily among the planimetry measurements, were identified; however, these outliers were retained for analysis as they did not significantly affect the overall statistical outcomes.
4. Results
The intra-rater reliability of the observer in this study was assessed using the ICC. The high ICC value (ICC = 0.9706) indicates excellent agreement between the two time points, confirming that the obtained data are reliable and suitable for analysis. The p-values listed in Table 1 correspond to statistical comparisons made among different reconstruction techniques (NV vs. PV), slice intervals (6 - 20), and sectional orientations (axial, sagittal, coronal), using one-way ANOVA followed by post-hoc analysis.
| Variables | Axial | Sagittal | Coronal | |||
|---|---|---|---|---|---|---|
| Technic | Mean ± SD | P-Value | Mean ± SD | P-Value | Mean ± SD | P-Value |
| NV6 | 1215.76 ± 789.69 | 0.810 | 1184.08 ± 788.16 | 0.948 | 1169.54 ± 795.07 | 0.828 |
| NV8 | 1211.97 ± 794.51 | 0.837 | 1191.2 ± 792.38 | 0.920 | 1172.8 ± 788.4 | 0.846 |
| NV10 | 1209.21 ± 797.22 | 0.856 | 1183.97 ± 789.16 | 0.911 | 1169.14 ± 787.78 | 0.874 |
| NV12 | 1211.17 ± 816.25 | 0.920 | 1189.84 ± 788.27 | 0.995 | 1162.43 ± 783.7 | 0.774 |
| NV16 | 1200.33 ± 821.55 | 0.995 | 1183.09 ± 815.42 | 0.883 | 1167.32 ± 790.71 | 0.783 |
| NV20 | 1198.44 ± 785.9 | 0.958 | 1188.52 ± 806.18 | 0.930 | 1156.22 ± 788.14 | 0.729 |
| PV6 | 1229.32 ± 792.48 | 0.729 | 1198.33 ± 787.73 | 0.986 | 1183.84 ± 795.94 | 0.939 |
| PV8 | 1223.03 ± 795.68 | 0.738 | 1212.04 ± 795.22 | 0.930 | 1186.72 ± 790.48 | 0.948 |
| PV10 | 1220.62 ± 799.26 | 0.837 | 1198.09 ± 794.4 | 0.995 | 1183.93 ± 789.06 | 0.977 |
| PV12 | 1221.86 ± 818.07 | 0.846 | 1205.28 ± 790.23 | 0.911 | 1185.41 ± 792.78 | 0.893 |
| PV16 | 1212.87 ± 823.87 | 0.848 | 1196.49 ± 808.55 | 0.967 | 1183.88 ± 790.26 | 0.874 |
| PV20 | 1215.6 ± 792.15 | 0.846 | 1204.68 ± 807.78 | 0.930 | 1171.1 ± 788.29 | 0.792 |
It is evident from Table 1 that the volume values for each parameter closely align with those obtained using Archimedes' method. The results of the Mann-Whitney U test indicate no statistically significant difference between the techniques (P > 0.05).Similarly, no significant difference was observed between the different slice intervals for either technique (P > 0.05) (Table 2). Furthermore, when examining section orientation, no difference was found between the orientations (P > 0.05) (Table 3).
Mann-Whitney U Test Results for the Comparison of Multiple Variables Between the Techniques and the Different Slice Intervals
| Orientation | P-Value a |
|---|---|
| Axial | 0.897 |
| Sagittal | 0.888 |
| Coronal | 0.901 |
Mann-Whitney U Test Results for the Comparison of Section Orientation
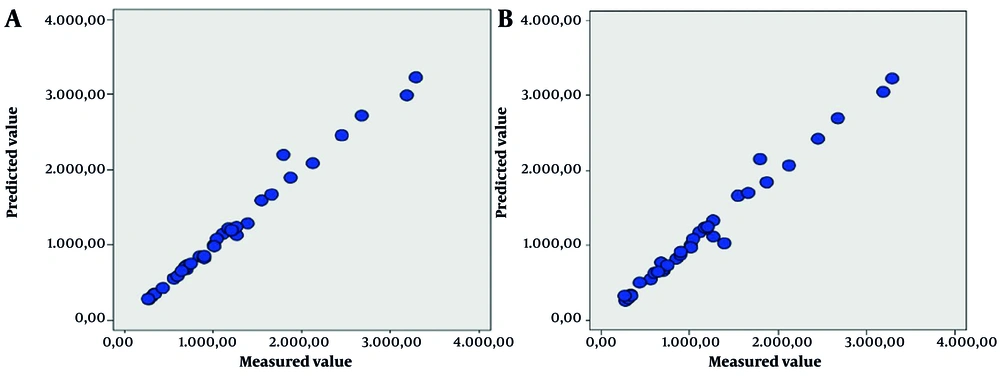
The agreement between Archimedes' data and both section orientation and slice intervals was assessed using ICC analysis. A two-way random-effects model with absolute agreement was applied. The ICC value for section orientation was 0.951 (95% CI, 0.90 - 0.98), while for slice intervals, it was 0.923 (95% CI, 0.90 - 0.98). These results indicate a high level of agreement between the methods and Archimedes' data. The reliability of the measurements was statistically significant (P < 0.001) (Figure 3).
Scatter plots illustrating the relationship between measured and predicted volume values. A, Volumetric measurements based on different section orientations; B, Volumetric measurements across varying slice intervals. The linear trend in both graphs indicates high consistency between predicted and actual data.
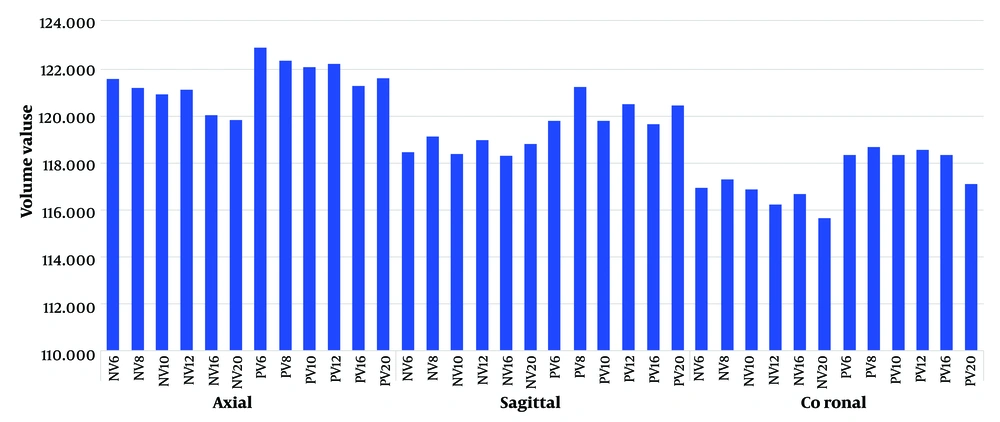
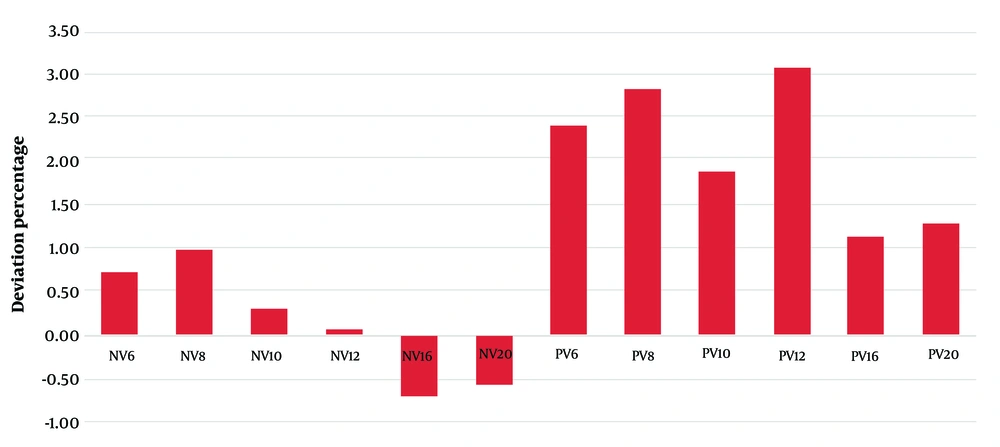
Despite the absence of a statistically significant difference among all evaluations, some deviations were observed. Figure 4, a graphical representation of the data, clearly shows that in every evaluation, the volume values determined by the planimetry technique are consistently greater than those determined by the point counting technique. No statistically significant difference was found in the percentages of deviations between the methods (P = 0.628).However, it is evident that the point-counting method tends to underestimate the measurements (Figure 5).
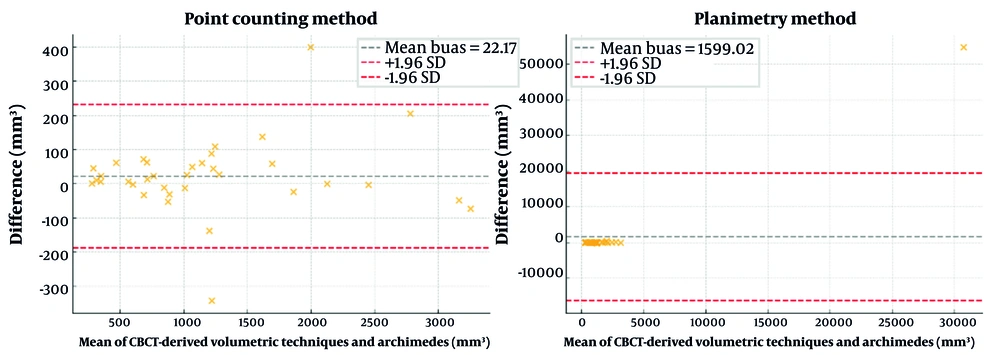
Bland-Altman plots were generated to assess the agreement between the CBCT-derived mean volumes (across different slice intervals) and the Archimedes measurements for both the point counting and planimetry methods. The plots demonstrated good agreement, with no significant systematic bias observed (Figure 6).
The mean percentage errors between CBCT-derived volumetric techniques and Archimedes-derived measurements are presented in Table 4. The point-counting method exhibited a mean percentage error of +2.63% (± 7.96), indicating close agreement with the reference standard. The planimetry method showed a higher mean percentage error of +51.11% (± 277.68), reflecting greater variability across measurements.
| Method | Mean Percentage Error (%) | Standard Deviation (%) |
|---|---|---|
| Point counting | 2.63 | 7.96 |
| Planimetry | 51.11 | 277.68 |
Mean Percentage Error Between Cone-beam Computed Tomography-Derived and Archimedes-Derived Volume Measurements
5. Discussion
This study investigated the impact of section orientation and slice interval on volumetric measurements obtained from CBCT images using point-counting and planimetry methods. Our findings demonstrate that neither section orientation nor slice interval variations had a statistically significant effect on the accuracy of volumetric estimations. This suggests that while these two parameters may influence individual measurements, they do not substantially alter the overall volumetric assessment. The high ICC values observed for both section orientation and slice intervals further support this conclusion, indicating strong agreement between the different measurement conditions and the gold standard, Archimedes' principle. These results have important implications for clinical practice, as they suggest that clinicians can be confident in the accuracy of volumetric measurements obtained from CBCT images regardless of the chosen section orientation or slice interval within the tested ranges. Both planimetry and point-counting approaches, based on the assumptions of the Cavalieri method, are stereological techniques for determining volume. Different conclusions have been drawn when comparing the outcomes of these approaches. According to numerous studies that have used the point-counting technique for organ volume estimations, the volumetric approach is superior to the planimetry technique (14). When assessing postmortem brain volume using MRI, Cotter et al. found that the point-counting technique is more effective than planimetry (26). Acer et al.'s investigation revealed a high degree of agreement between the outcomes derived from planimetry and point-counting methods. The amount of time needed for the assessment was the main difference between the two methods. The planimetry technique produced more accurate findings, while the point-counting technique was found to be faster (27). Koç et al. utilized CBCT imaging along with point-counting, manual segmentation, and semi-automatic segmentation techniques to evaluate intraosseous bone defects in bovine femoral condyles. Both manual and semi-automatic segmentation methods showed strong agreement with the Archimedes method.. However, the point-counting technique was found to be inconsistent with the volume estimations derived from the Archimedean approach (28). In this investigation, the planimetry and point-counting approaches demonstrated no statistically significant difference in volumetric estimations. The results obtained from both methods were consistent with the data derived from the Archimedes' principle, suggesting that both techniques can be reliably employed for volumetric assessments. While some deviations were observed, we attribute the lack of statistical significance to the size of the lesions. This interpretation is supported by the observation of similar discrepancies in the literature, where lesion size has been identified as a potential contributing factor. Furthermore, given the low probability of encountering large lesions in the maxillofacial region, our findings support the general applicability and interchangeability of these techniques in clinical practice. Additionally, percentage error analysis further confirmed the strong agreement between CBCT-derived and Archimedes-derived volumetric measurements.. The point-counting method exhibited a low mean error of +2.63% with minimal variability (± 7.96%), falling within clinically acceptable thresholds reported in the literature. In contrast, the planimetry method demonstrated a higher mean error rate of +51.11% (± 277.68%), potentially reflecting increased sensitivity to slice interval selection or manual delineation challenges. Despite this variability, the lack of statistically significant differences in volumetric measurements supports the general reliability of both techniques for clinical applications involving small and regular defects CT and MRI are the primary imaging modalities used in most studies that use the Cavalieri principle for volume estimations in the literature. For example, in a study involving domestic geese, Onuk et al. used the Cavalieri principle to compute the volumes of the nasal cavity and its structures from CT images. Physical parts of the structures were re-evaluated, and the results showed no statistical difference between the two approaches (29). In their investigation, Ertekin et al. employed CT scans to measure the intracranial and posterior cranial fossa volumes and performed volume computations using the point counting method. According to their research, the point counting approach is a useful tool for estimating volume and can produce precise volume estimations (30). Volume calculations employing sectional pictures obtained from CBCT systems have been the subject of relatively few studies, but their frequency has increased in recent years. Agbaje et al., for example, used a dry skull to automatically segment CBCT images in order to determine socket volumes. They found no discernible difference between the two methods when they compared the sockets' physical volumes as determined by Archimedes' method and the volumes obtained from the CBCT images (19). In a study, Kayipmaz et al. computed the volumes of defects really formed in the sheep's mandible and contrasted them with the volumes determined on CBCT images using the Cavalieri principle. When compared to one another, their results showed that the collected data were statistically comparable (21). Using the manual segmentation method, Bayram et al. computed the volumes of nine condyles from CBCT images taken from skulls. According to their findings, the quantities calculated using this method and the actual volumes were statistically consistent (31). Esposito et al. mimicked periapical lesions by simulating a defect in the cow jaw. There was no statistically significant difference between the two sets of volumes when they compared the volumes determined using CBCT with the volumes determined from the defect impression models (32). Using the manual segmentation method at different slice thicknesses, Sezgin et al. created a defect on the sheep's jaw and measured the volume of CBCT images. They found no significant difference between the volumes of the sockets as determined by Archimedes' method and those obtained from the CBCT images (16). In fact, CBCT has been used in many studies for a variety of dental applications, such as evaluating maxillary sinus volume, measuring mandibular condyles, assessing dental volumes, and examining the visibility of the inferior alveolar canal.
The Cavalieri principle can be used to calculate volume by splitting an image of the structure of interest into parallel sections and acquiring the image in the axial, coronal, or sagittal planes. Using CT images, Odaci et al. computed the stereological volumes of the lumbar vertebrae in the axial, sagittal, and coronal planes. They found no statistically significant differences in n the volumes they calculated in the various planes, suggesting that the accuracy of volume computations using the Cavalieri approach is not greatly affected by the choice of plane (33). Using CT scans, Bilgic et al. assessed the intervertebral disc volume in the axial, sagittal, and coronal planes. Their results showed that the accuracy of volume computations was not significantly affected by the plane selection, confirming the method's dependability (34). While no studies specifically evaluated CBCT images, similar evaluations were performed using CT scans. Our study contributes to this expanding body of work by examining the effect of volume estimations in CBCT images across the axial, sagittal, and coronal planes. Results show that slice orientation has no discernible effect on volumetric estimates. We speculate that this is due to the isotropic voxel structure of CBCT, which keeps voxel sizes constant in all three dimensions. The precision and reliability of the technique in this imaging modality are further supported by the consistency of volume computations across several planes in CBCT.
Slice thickness is a key variable influencing volumetric measurements on sectional images. Previous research has indicated that the accuracy of volume estimates derived from images is significantly impacted by slice thickness. Specifically, narrower slices tend to reduce the risk of underestimation, while variations in slice thickness have been associated with inflated and imprecise volume estimations (20, 22). One of the aims of the present study was to evaluate the impact of slice interval variations on CBCT-based volumetric calculations. Although our findings revealed some variability in measurements across different slice intervals, these differences did not reach statistical significance, which may be attributed to the relatively small size of the simulated lesions. Nevertheless, considering the theoretical potential for increased measurement error with wider slice intervals, we recommend, from a clinical and practical perspective, using the smallest feasible slice interval. One limitation of this study is that volumetric measurements were performed by a single observe. Although the intra-rater reliability was excellent, future studies involving multiple observers are recommended to further validate reproducibility and to minimize potential observer bias. Despite certain limitations, this study provides valuable insights. While bovine femurs are a widely accepted surrogate for human bone, inherent inter-species differences must be acknowledged. Additional studies that include several observers and a broader range of volumetric techniques will help address inter-observer variability and practical considerations such as ease of use and processing time. Finally, although the defects in this study were created with varying depths and irregular shapes to mimic the heterogeneity of clinical bone lesions, real pathological lesions may exhibit even greater morphological complexity; therefore, validation in clinical settings is recommended. Pursuing these future directions will build on the present findings and contribute to a more comprehensive understanding of volumetric analysis.
In conclusion, this study examined how section orientation and slice interval affect the accuracy of CBCT-based volumetric measurements obtained with point-counting and planimetry methods, using Archimedes’ principle as the reference standard. Within the tested ranges, neither parameter had a statistically significant impact on volumetric estimates. Although minor deviations were detected, they did not reach statistical significance. These findings corroborate the reliability of CBCT for stereological volume calculations. Future research should evaluate these parameters in larger or more complex lesions and explore protocol refinements that could further optimize CBCT for specific clinical applications.