Abstract
Background:
Brain segmentation from diffusion tensor imaging (DTI) into white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) with acceptable results is subjected to many factors.Objectives:
The most important issue in brain segmentation from DTI images is the selection of suitable scalar indices that best describe the required tissue in the images. Specifying suitable clustering method and suitable number of clusters of the selected method are other factors which affects the segmentation process significantly.Materials and Methods:
The segmentation process is evaluated using four different clustering methods with different number of clusters where some DTI scalar indices for 10 human brains are processed.Results:
The aim was to produce results with less segmentation error and a lower computational cost while attempting to minimizing boundary overlapping and minimizing the effect of artifacts due to macroscale scanning.Conclusion:
The volume ratios of the best produced outputs with respect to the total brain size are 16.7% ± 3.53% for CSF, 35.05% ± 1.13% for WM, and 48.2% ± 2.88% for GM.Keywords
Brain Segmentation Diffusion Tensor Diffusion Volume DTI Clustering
1. Background
The segmentation of medical images of the brain has an important impact in modeling and diagnosing the brain’s structure and function. However, the segmentation process still cannot be accomplished in an automatic manner; therefore, simple segmentation methods, such as the threshold method, are still used in a large scope and experts enhance the produced results manually. The selection of suitable threshold value to separate gray matter (GM) (that constitutes almost 50% of whole brain components (1-3)), white matter (WM) (that constitutes almost 37% of whole brain components (1-3)), and cerebrospinal fluid (CSF) (that constitutes almost 13% of whole brain components (1-3)) is also another question of whether many values are suggested even within the same medical imaging modality (4-7).
1.1. Diffusion Tensor Imaging (DTI)
Live tissue in any part of the body is assumed to be almost uniform (8), which is reflected in medical images such as magnetic resonance imaging (MRI) (9) and computed tomography scan (CT-scan) (10) as areas of almost the same greyscale. Other modalities such as diffusion tensor imaging (DTI) (11) can produce more data that describe tissues’ fiber structure in terms of eigenvalues and eigenvectors (11-16). More details about DTI can be found in the appendix.
1.2. Rotational Invariant Quantities
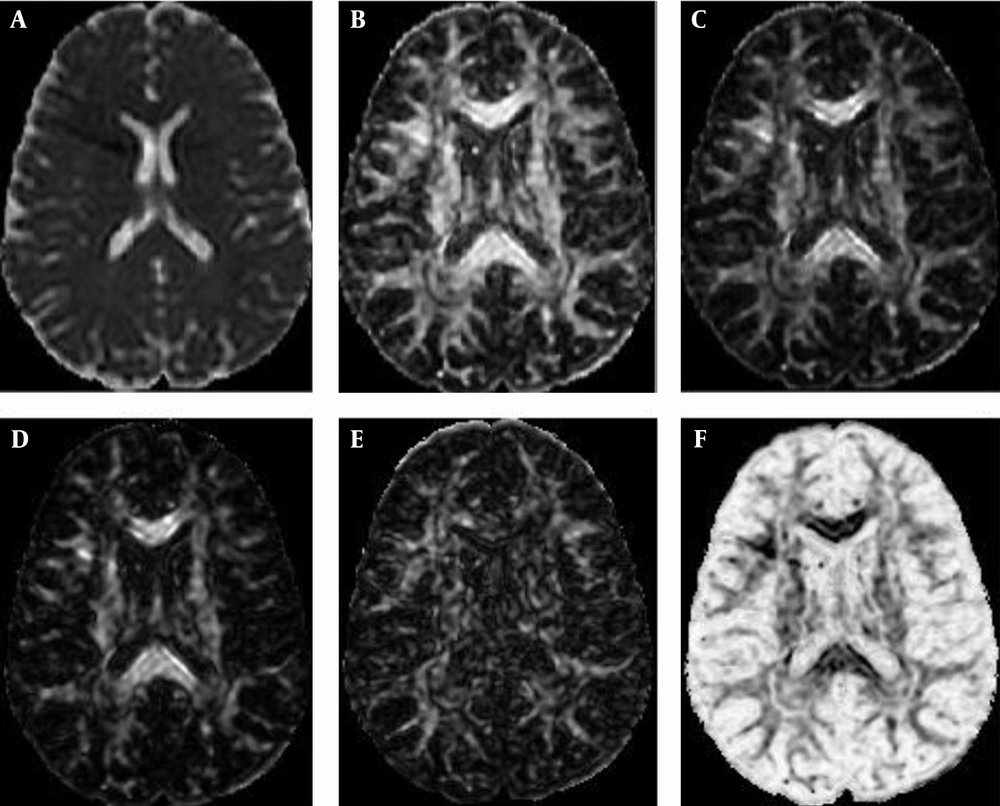
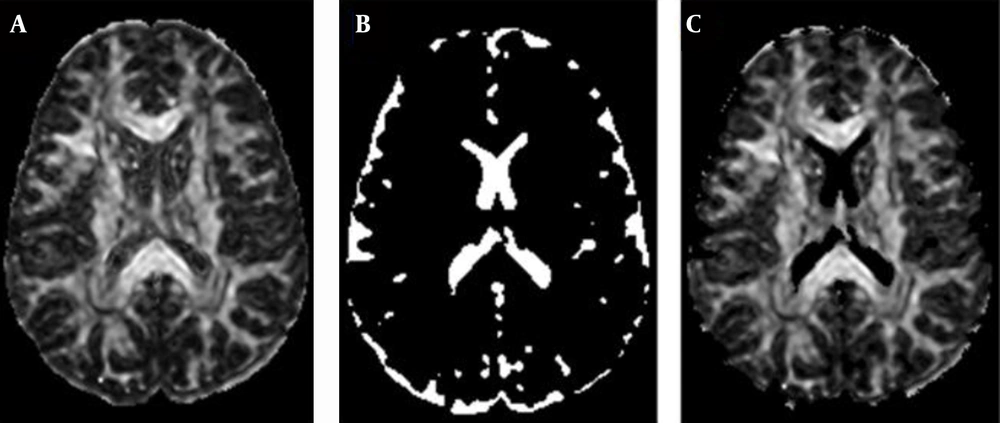
The direction of the fibers varies from one location to another location; thus, rotational invariant quantities (called also scalar indices) are required to describe the diffusion of each element in the sample (scalar indices are presented as following formulas). Many methods are derived to provide the rotational invariant quantities of diffusion, which include mean diffusivity, rational anisotropy, fractional anisotropy, skewness, linear-anisotropy, planner-anisotropy, and isotropy (11-15). By processing DTI data using rotational invariant quantities, more meaningful images can be produced to help in distinguishing between different tissues referring to their structure (Figure 1).
Mean diffusivity (MD):
Fractional anisotropy (FA):
Rational anisotropy (RA):
Linear anisotropy (CL):
Planner anisotropy (CP):
Spherical anisotropy (CS):
Diffusion volume (DV):
The diffusion volume (DV) scalar index (17, 18) reflects the relative amount of water in tissues, referring to the working methodology of the MRI scanner that depends on the spinning property of water molecules in tissue (11, 19, 20). Regions with large amounts of water, such as blood and CSF, thus have large values and regions with small amounts of water, such as fats, muscles, WM, and GM, have lower values (2, 3, 16, 18, 20).
1.3. Segmentation Problems
In general, according to the resolution limitation of the scanner, it is only possible to generate macroscale images such that the unit area in an image will represent the average property of the corresponding group of tissues at that zone (11, 13). The limitation of the macroscale will lead to a problem in the boundary that separates two different types of tissues in the image; during the segmentation process, it would be difficult to assume whether a point at that boundary belongs to the first tissue or to the other tissue, or whether there is a boundary overlapping problem. The noise produced from artifacts is another problem in medical imaging that affects the segmentation process for areas of the same type of tissue (16, 21, 22)
1.4. Image Segmentation Methods
In general, the segmentation of the brain structure from MRI, diffusion weighted imaging (DWI), and DTI has been accomplished using the boundary-based methods and the hybrid methods, particularly the level-set method or using labeling (23); however, region-based methods are more widely used in medical image segmentation (13, 18, 21, 22, 24-28)
Region-based methods rely on clustering algorithms such as Otsu’s (29), K-means (30), expectation maximization (EM) (31), C-means (32), and the simple manual threshold method. The Markov random field (MRF) and its models, such as iterated conditional modes (ICM), are widely used in region-based image segmentation processes (21, 22, 27, 28). It should be taken into consideration that there is no unique solution for the segmentation problem (21, 22, 28) whereby changing the number of clusters leads to different results.
2. Objectives
This paper is a comparative study of different clustering techniques applied on some DTI scalar indices that can be used in the segmentation of the brain’s DTI images. Here, problems of suitable scalar index selection, suitable clustering algorithms, and the suitable number of clusters are addressed by taking into consideration minimizing boundary overlapping and minimizing the effect of artifacts during the segmentation process.
3. Materials and Methods
3.1. Data Acquisition and Preprocessing
Datasets of 10 healthy human brains were acquired from John Hopkins medical institute. These datasets consist of volumes of brain DTI data. Each brain DTI volume contains 50 slices of 256×256 voxels per slice. Each dataset has a file consisting of 35 gradient orientations used to calculate tensor data (eigenvalues and eigenvectors). (The voxel width = 0.9375 mm, the voxel height =0.9375 mm, and the space between two successive slices = 2.5 mm in every slice).
DTI-Studio (a special utility that manages raw DTI data) was used to calculate the three eigenvalues and their corresponding three eigenvectors for every voxel in addition to some of the scalar indices. Before performing the segmentation process; the scalp, skull, skin, and other noisy materials surrounding the brain tissues were removed (this is the only manual operation in the segmentation process).
3.2. Parameters and Data Selection
A clear understanding of the detailed structure of the brain components in addition to the working principal of the DTI scanner will lead to better selection of the suitable scalar index that best describes the targeted tissue according to its biological characteristics (2, 3). From these characteristics, it is concluded that CSF contains the largest amount of water and WM and GM contain the least. Moreover, the arrangement of the contained water for each of these components differs, as the water content of CSF is completely free (isotropic), but that of WM is arranged in axon cells (very restricted or highly anisotropic). The arrangement of the water content of GM is not as sharply restricted as WM and not as free as CSF. Thus, it is possible to employ the eigenvalues, the MD or the DV in the classification of the CSF and non-CSF regions, and rational quantities such as the FA, the RA, or the VR, could be employed to differentiate between the WM and non-WM regions.
It was reported that the eigenvalues of CSF diffusion are more than double the GM and WM values (4) and a threshold in the MD map that is greater than 1.05 × 10-3 mm2/s will separate the CSF and non-CSF components (5). However, a threshold in the normalized FA map that is greater than 0.25 (if the CSF is not removed and greater than 0.35 if the CSF has been removed) would be sufficient to separate the WM and non-WM components (6, 7) where it is proven to provide a good estimation of different tissues structures (14). This baseline information could be used as reference to identify the quality of the produced results later on.
Region-based segmentation methods are widely used in medical imaging segmentation, which makes them the preferred choice for this task. However, the selection of the best clustering algorithm with a suitable number of clusters is another issue that is addressed in this paper in which accurate results, lower computational costs, and the guarantee of artifact reduction are taken into consideration.
3.3. CSF/Non-CSF Tissue Segmentation
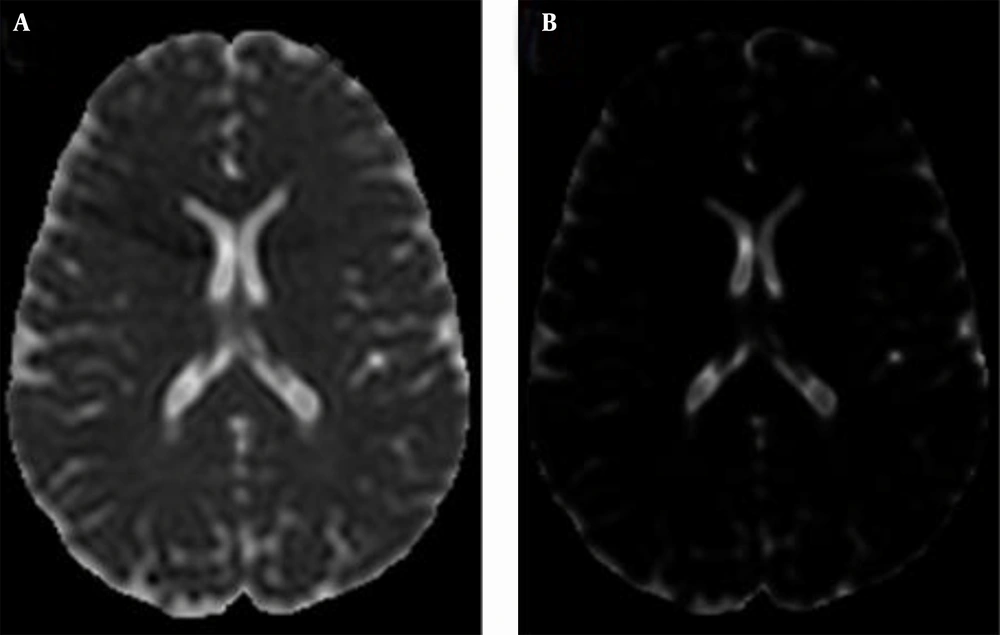
To analyze the data on the 10 brains included in this study, the MD and the DV scalar indices were used to generate MD and DV images, respectively. These images are normalized greyscale images (Figure 2).
Some scalar indices of a human brain where A, Mean diffusivity; B, Fractional anisotropy; C, Rational anisotropy; D, Linear anisotropy; E, Planner anisotropy, and F, Spherical anisotropy.
Cross-section in a human brain that shows A, The mean diffusivity image that is produced from the mean diffusivity scalar index; and B, The diffusion volume image that is produced from the diffusion volume scalar index for the same slice.
Referring to the biological and physiological data of brain components and the working methodology of the MRI scanner, lighter regions in these images correspond to regions with more water, and this represents CSF. However, darker regions correspond to regions with less water than lighter ones, representing WM and GM (non-CSF).
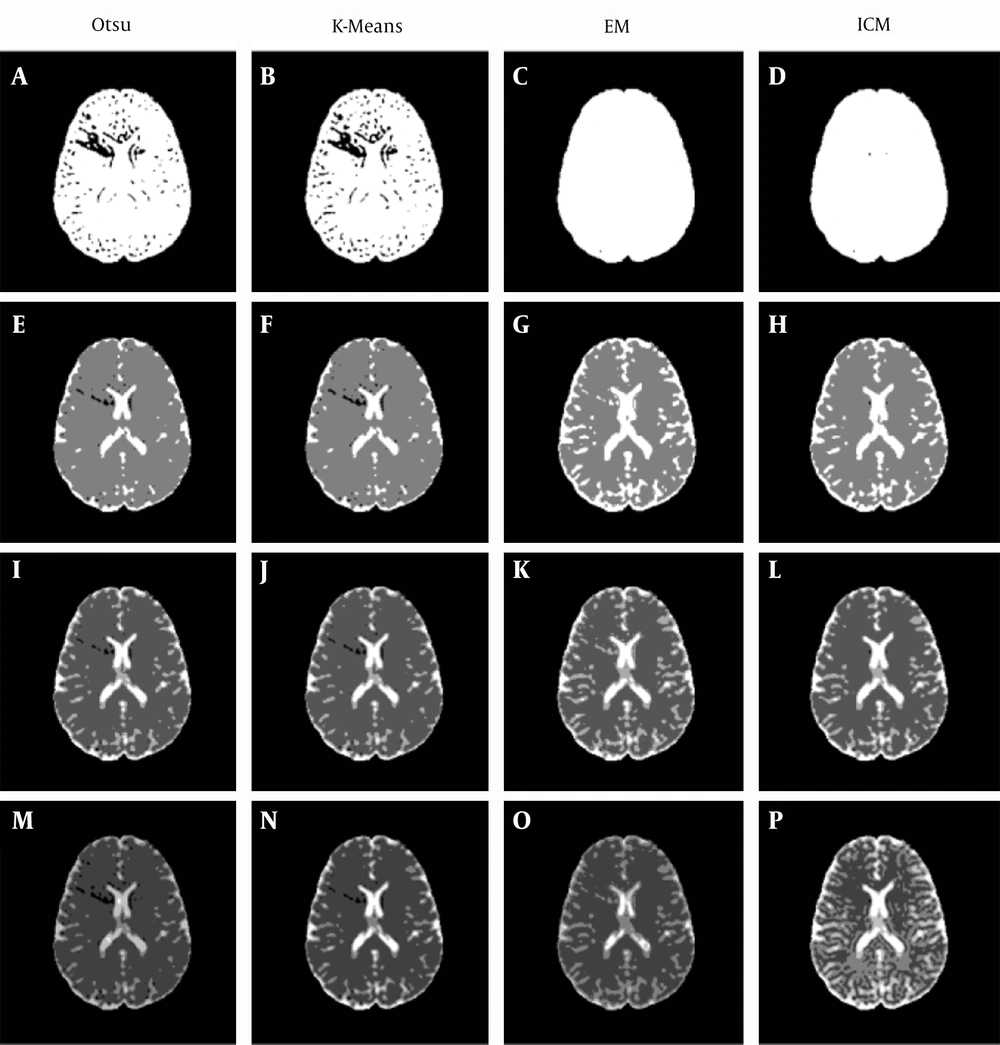
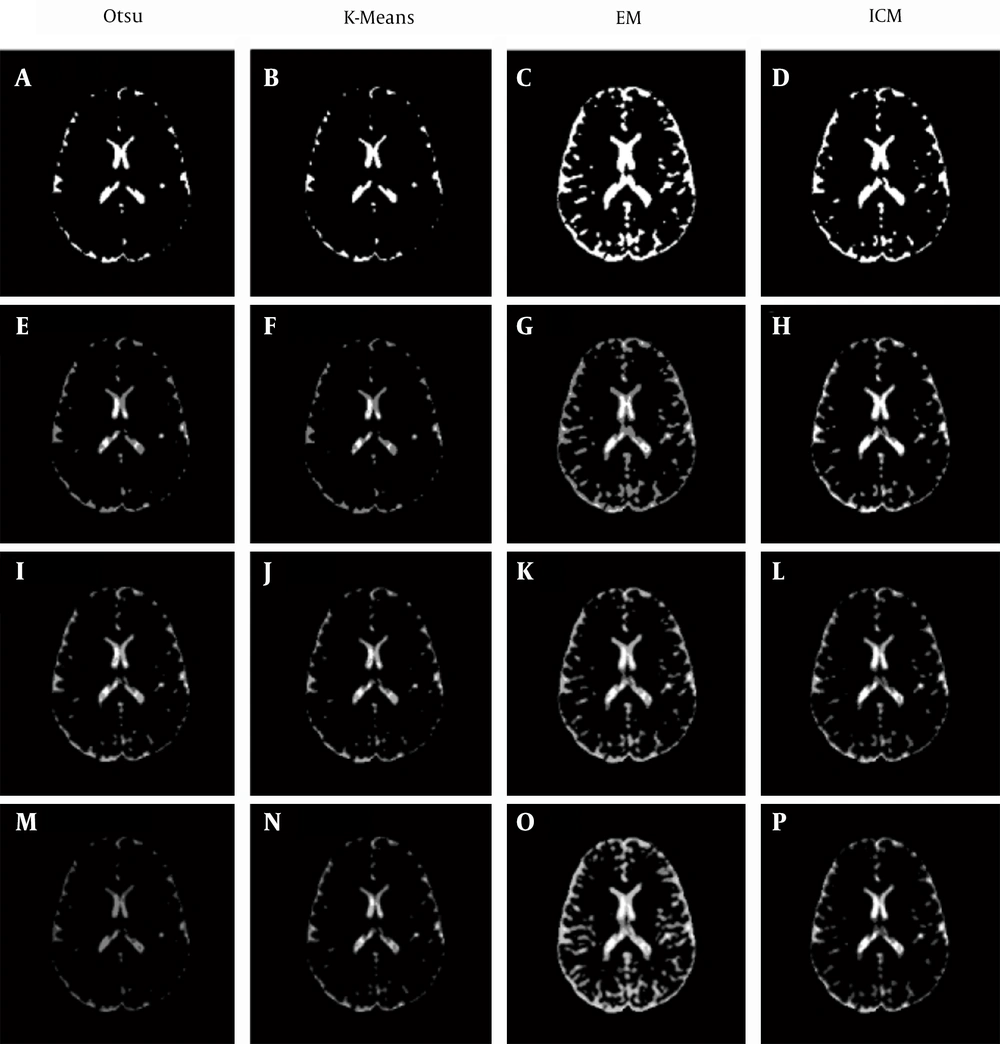
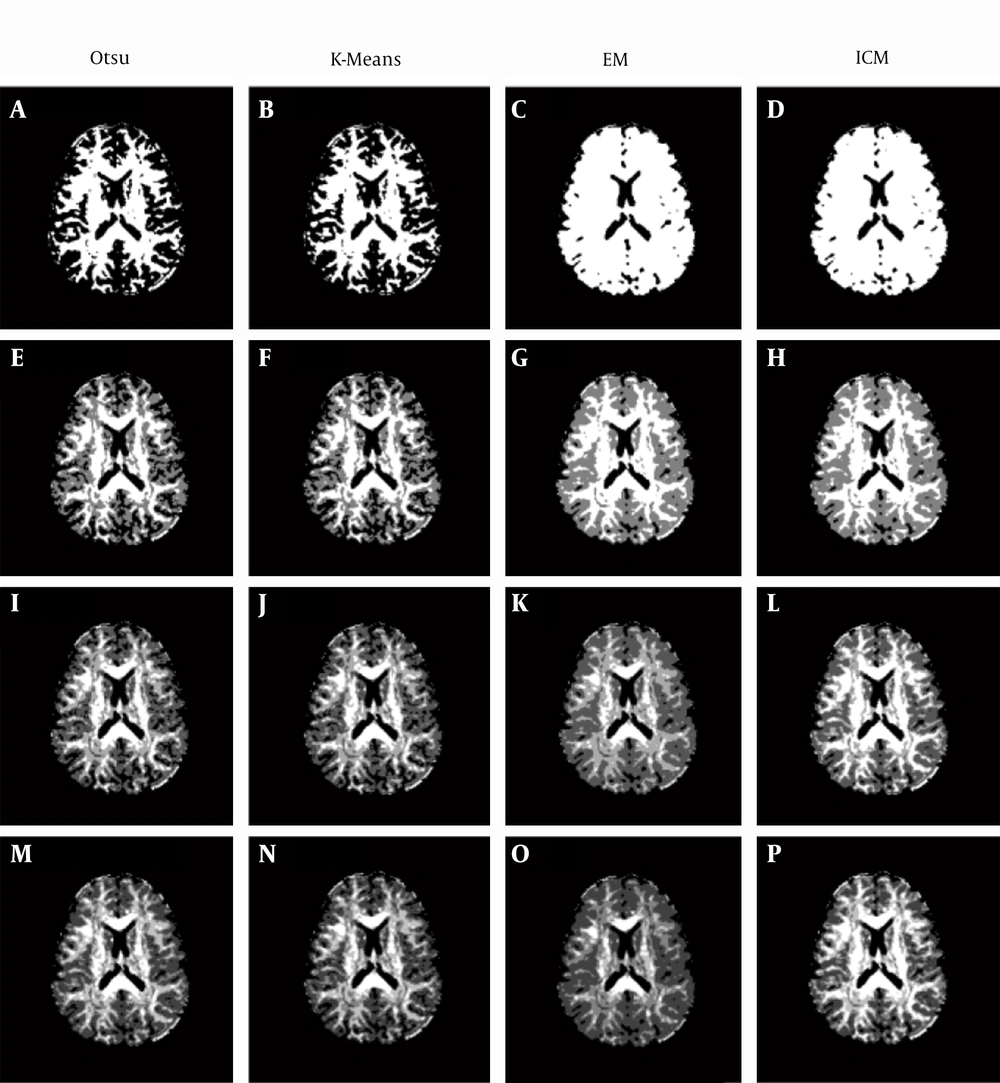
Four clustering methods are applied to the MD and DV images with different numbers of clusters: Otsu’s, K-means, EM, and ICM methods (using MATLAB tool box (15)). When Otsu’s method is being applied to MD images and the number of clusters is set to two, then it is written as Otsu2-MD and so on for other settings.
For the MD images (Figure 3), when two clusters are used, the produced clustering maps are significantly unreadable (Figure 3 A - D) because the non-CSF tissues’ intensities are closer to the CSF regions’ intensities. In this case, it would be better to use three (Figure 3 E - H) or four clusters (Figure 3I - L) to produce more readable clustering maps.
Clustering maps of an mean diffusivity image using different methods. A, Otsu2-MD; B, K-means2-MD; C, EM2-MD; D, ICM2-MD; E, Otsu3-MD; F, K-means3-MD; G, EM3-MD; H, ICM3-MD; I, Otsu4-MD; J, K-means4-MD; K, EM4-MD; L, ICM4-MD.
However, for the DV images (Figure 4), when two clusters are used, the produced clustering maps are quite readable (Figure 4A - D) because the non-CSF tissues’ intensities are closer to the background color; even when increasing the number of clusters to three (Figure 4E - H) or four clusters (Figure 4 E - H), slight changes are produced.
Clustering maps of a diffusion volume image using different methods. A, Otsu2-DV; B, K-means2-DV; C, EM2-DV; D, ICM2-DV; E, Otsu3-DV; F, K-means3-DV; G, EM3-DV; H, ICM3-DV; I, Otsu4-DV; J, K-means4-DV; K, EM4-DV; L, ICM4-DV.
Regions with a lighter color (white) within MD-based clustering maps correspond to regions that are most likely to be considered CSF regions. It should be noted that there is a significant reduction in these white regions with an increasing number of clusters, which reflects the significant effect of the number of clusters on MD-based clustering maps.
This is not the case for DV-based clustering maps, in which all of the non-black colors of DV images represent regions that are the most likely to be considered CSF regions. With an increasing number of clusters, the change in non-black regions (occupying more points from the boundary between the CSF and non-CSF regions) is relatively small, which makes DV-based clustering maps less sensitive to the change in the number of clusters.
The best methods for the segmentation of CSF/non-CSF tissues that achieve the closest ratios to real measurements are as follows: Otsu3-MD, K-means3-MD, K-means7-DV, K-means8-DV, and ICM2-DV. However, the selected method is ICM2-DV in which the reduction of noise produced due to artifacts is guaranteed. Further justification for these results will be provided later.
3.4. WM/Non-WM Tissue Segmentation
According to the brain structure, the remarkable feature of WM is its higher anisotropy than other parts of the brain; the FA scalar index can be used to identify the WM/non-WM parts of the brain. Referring to the biological and physiological data of the brain components, lighter regions in FA images (Figure 5A) correspond to tissues of high anisotropy, which represents WM. However, darker regions correspond to regions of less anisotropy than the lighter ones; this represents GM and CSF (non-WM).
A, Normalized fractional anisotropy map; B, Cerebrospinal fluid clustering map (ICM2-DV clustering map); C, Normalized fractional anisotropy image after removing cerebrospinal fluid.
By applying the used clustering methods (Otsu, K-means, EM, and ICM) to FA images after removing the CSF regions using the ICM2-DV method (Figure 5), the produced FA-based clustering maps (Figure 6) face the non-unique solution of clustering problem. Regions with a lighter color (white) within FA-based clustering maps correspond to regions that are most likely to be considered the WM regions; significant reductions in these regions increase the number of clusters, except for the ICM method in which the reduction is relatively much smaller.
Clustering maps of an fractional anisotropy image using different methods. A, Otsu2-FA; B, K-Means2-FA; C, EM2-FA; D, ICM2-FA; E, Otsu3-FA; F, K-Means3-FA; G, EM3-FA; H, ICM3-FA; I, Otsu4-FA; J, K-Means4-FA; K, EM4-FA; L, ICM4-FA.
The best methods for the segmentation of the WM/non-WM tissues that achieve the closest ratios to real measurements are ICM3-FA and EM3-FA. However, the selected method is ICM3-FA for two reasons: the reduction of the noise produced due to artifacts and the lowest relative error compared to the threshold method. Further justification for these results will be provided later.
3.5. Brain Tissue Reconstruction
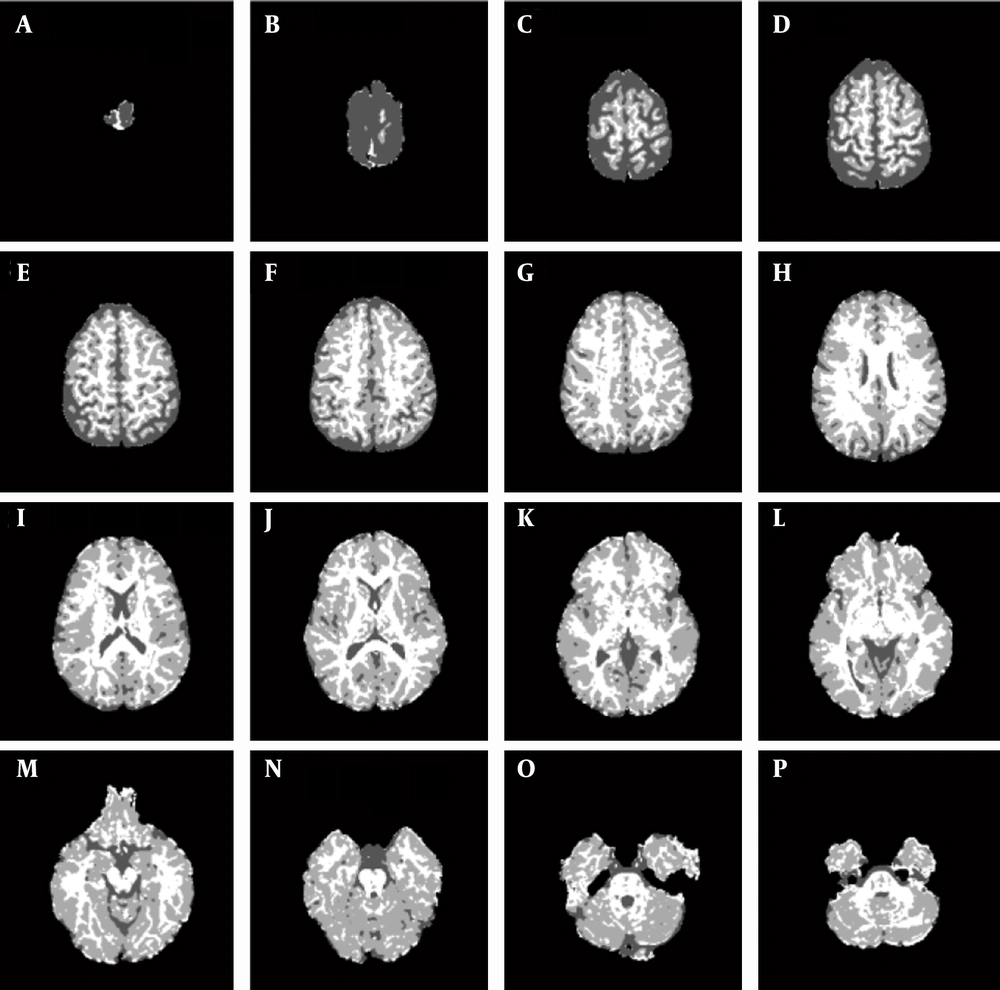
Finally, it is possible to reconstruct the brain into maps that show brain tissues as regions with different colors (Figure 7).
Clustering maps of the brain components at different levels with level ID in the corner (WM = White, GM = Light gray and CSF = Dark. A, level ID = 48; B, level ID = 45; C, level ID = 42; D, level ID = 39; E, level ID = 36; F, level ID = 33; G, level ID =30; H, level ID = 27; I, level ID = 24; J, level ID = 21; K, level ID = 18; K, level ID = 15; M, level ID = 12; N, level ID = 9; O, level ID = 6; P, level ID = 3.
The ICM2-DV method is used to identify the CSF regions, the ICM3-FA method is used to identify WM regions, and the remaining parts are the GM regions. The volume ratios of these maps are 16.7% ± 3.53% for CSF, 35.05% ± 1.13% for WM, and 48.2% ± 2.88% for GM, and these results are close to the ratios reported in the literature (13% for CSF, 37% for WM and 50% for GM).
4. Results
4.1. CSF/Non-CSF Tissue Segmentation Results
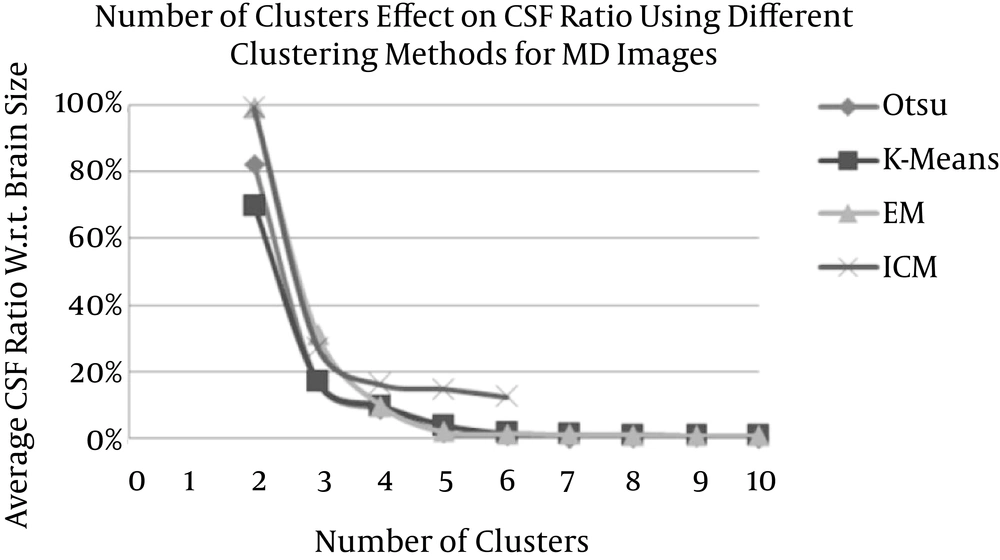
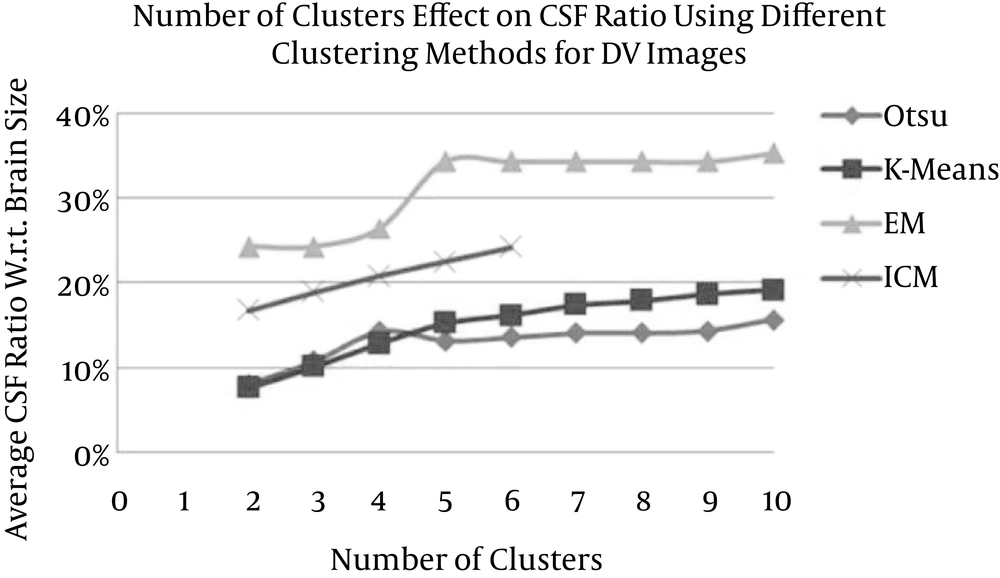
By measuring the CSF ratio (that is derived from Otsu’s, K-means, EM, and ICM methods) with respect to the total brain size as well as measuring the CSF relative error (RE) with respect to the CSF regions of a reference model (which are extracted from the MD images using the threshold method) for different numbers of clusters (2 to 10 clusters in the case of Otsu, K-means, and EM and 2 to 6 in the case of ICM) for both the MD and the DV images (Tables 1 and 2), the variation in the CSF ratio is decreasing (because one cluster is selected to represent the CSF and the other cluster for the non-CSF) to zero with a relatively fast rate in accordance to the increase in the numbers of clusters for Otsu’s, K-means, and EM methods.
Average Cerebrospinal Fluid Ratio and Average Relative Error of Mean Diffusivity Images
| # of Clusters | Otsu | K-Means | EM | ICM | ||||
|---|---|---|---|---|---|---|---|---|
| CSF (%) | RE (%) | CSF (%) | RE (%) | CSF (%) | RE (%) | CSF (%) | RE (%) | |
| 2 | 82.21 ± 24.28 | 391.61 ± 229.54 | 69.60 ± 29.83 | 327.84 ± 264.14 | 99.02 ± 0.06 | 472.50 ± 161.90 | 98.99 ± 0.06 | 472.34 ± 161.93 |
| 3 | 16.84 ± 3.27 | 7.79 ± 3.79 | 16.77 ± 3.23 | 8.13 ± 3.58 | 30.85 ± 3.80 | 76.25 ± 24.62 | 26.85 ± 2.81 | 54.49 ± 24.35 |
| 4 | 8.69 ± 4.00 | 52.48 ± 17.93 | 9.55 ± 2.75 | 48.95 ± 6.78 | 9.40 ± 5.44 | 46.19 ± 29.43 | 15.81 ± 3.24 | 48.35 ± 64.26 |
| 5 | 1.60 ± 3.01 | 91.34 ± 15.70 | 3.67 ± 2.22 | 79.92 ± 10.63 | 1.80 ± 0.49 | 89.76 ± 3.78 | 14.52 ± 3.68 | 66.75 ± 66.74 |
| 6 | 0.48 ± 0.78 | 97.28 ± 4.46 | 1.45 ± 0.32 | 91.99 ± 1.26 | 1.11 ± 0.11 | 93.72 ± 1.30 | 12.20 ± 2.34 | 41.28 ± 22.81 |
| 7 | 0.00 ± 0.00 | 100.00 ± 0.00 | 1.03 ± 0.12 | 94.24 ± 0.90 | 0.88 ± 0.08 | 95.04 ± 0.89 | - | - |
| 8 | 0.00 ± 0.01 | 99.99 ± 0.03 | 0.82 ± 0.11 | 95.39 ± 0.73 | 0.77 ± 0.10 | 95.69 ± 0.67 | - | - |
| 9 | 0.13 ± 0.28 | 99.29 ± 1.60 | 0.64 ± 0.13 | 96.44 ± 0.61 | 0.62 ± 0.08 | 96.52 ± 0.56 | - | - |
| 10 | 0.00 ± 0.00 | 100.00 ± 0.00 | 0.50 ± 0.06 | 97.20 ± 0.49 | 0.50 ± 0.08 | 97.23 ± 0.44 | - | - |
Average Cerebrospinal Fluid Ratio and Average Relative Error of Diffusion Volume Images
| # of Clusters | Otsu | K-Means | EM | ICM | ||||
|---|---|---|---|---|---|---|---|---|
| CSF (%) | RE (%) | CSF (%) | RE (%) | CSF (%) | RE (%) | CSF (%) | RE (%) | |
| 2 | 8.05 ± 2.92 | 57.78 ± 10.45 | 7.62 ± 2.85 | 60.10 ± 10.4 | 24.30 ± 3.50 | 38.98 ± 11.35 | 16.74 ± 3.53 | 8.86 ± 2.49 |
| 3 | 10.78 ± 3.08 | 42.29 ± 7.17 | 10.12 ± 2.92 | 45.90 ± 7.05 | 24.30 ± 3.50 | 38.98 ± 11.35 | 18.89 ± 3.12 | 10.63 ± 5.46 |
| 4 | 14.27 ± 3.20 | 22.01 ± 8.73 | 12.87 ± 2.82 | 30.06 ± 4.61 | 26.51 ± 3.07 | 57.02 ± 53.88 | 20.80 ± 3.25 | 20.03 ± 8.68 |
| 5 | 13.17 ± 3.22 | 27.79 ± 13.38 | 15.28 ± 3.27 | 16.82 ± 2.99 | 34.32 ± 4.62 | 99.65 ± 49.21 | 22.52 ± 3.13 | 29.58 ± 12.13 |
| 6 | 13.64 ± 4.53 | 28.23 ± 10.19 | 16.18 ± 3.49 | 11.86 ± 3.23 | 34.32 ± 4.62 | 99.65 ± 49.21 | 24.22 ± 3.02 | 39.28 ± 15.91 |
| 7 | 14.11 ± 2.40 | 22.67 ± 8.47 | 17.43 ± 2.79 | 8.64 ± 4.39 | 34.32 ± 4.62 | 99.65 ± 49.21 | - | - |
| 8 | 14.13 ± 2.55 | 22.37 ± 8.66 | 17.95 ± 2.89 | 8.02 ± 4.43 | 34.32 ± 4.62 | 99.65 ± 49.21 | - | - |
| 9 | 14.37 ± 3.76 | 22.08 ± 9.54 | 18.68 ± 3.13 | 9.63 ± 5.49 | 34.32 ± 4.62 | 99.65 ± 49.21 | - | - |
| 10 | 15.67 ± 2.60 | 14.39 ± 3.70 | 19.15 ± 3.20 | 11.49 ± 4.90 | 35.34 ± 4.11 | 104.24 ± 43.97 | - | - |
However, in the ICM method, the CSF ratio decreased rapidly at the beginning and then decreased at a lower rate (Figure 8).
Average CSF ratio (with respect to total brain volume) versus various numbers of clusters for Otsu’s, K-means, EM, and ICM methods when employed for the MD map. (CSF, cerebrospinal fluid; MD, mean diffusivity).
This is not the case for DV clustering maps; as the number of clusters increase, the CSF ratio increases (because all clusters are selected to represent CSF except one cluster for non-CSF) at relatively low rates (Figure 9).
Average CSF ratio (with respect to total brain volume) versus various numbers of clusters for Otsu’s, K-means, EM, and ICM methods when employed for the DV map. (CSF, cerebrospinal fluid; DV, Diffusion Volume).
Referring to the calculated relative errors, the best settings for the segmentation of CSF tissue that achieve the closest CSF ratios to the reference model would be as follows: Otsu3-MD (16.84% ± 3.27%), K-means3-MD (16.77% ± 3.23%), K-means7-DV (17.43% ± 2.79%), K-means8-DV (17.95% ± 2.89%), and ICM2-DV (16.74% ± 3.53%). The selected setting is ICM2-DV, which achieves a closer CSF ratio to the measured values in the literature, the RE is relatively small, the computational cost is relatively small, and noise reduction is guaranteed.
4.2. WM / Non-WM Tissue Segmentation Results
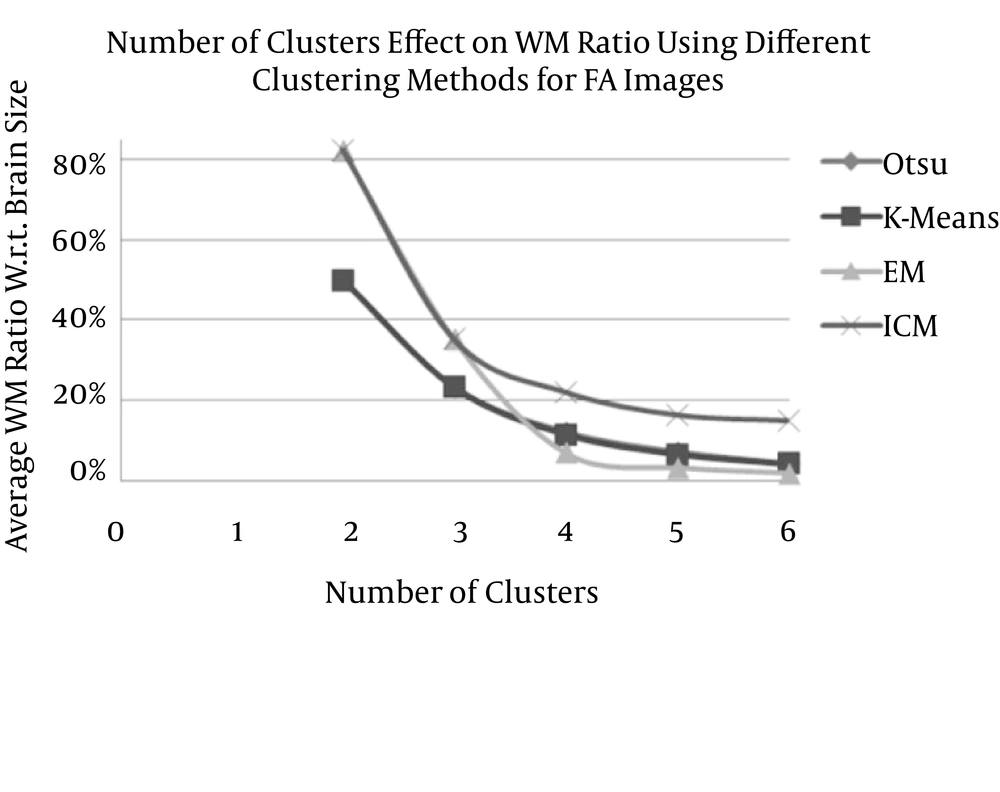
By measuring the produced WM ratio with respect to the total brain size as well as measuring the WM relative error with respect to the WM regions of a reference model (which are extracted from FA images using the threshold method) for different numbers of clusters (2 to 6 clusters) for FA images (Table 3), the variation in the WM ratio decreases at a relatively fast rate in accordance with increasing numbers of clusters for Otsu’s, K-means, and EM methods.
Average White Matter Ratio and Average Relative Error of Fractional Anisotropy Images
| # of Clusters | Otsu | K-Means | EM | ICM | ||||
|---|---|---|---|---|---|---|---|---|
| WM (%) | RE (%) | WM (%) | RE (%) | WM (%) | RE (%) | WM (%) | RE (%) | |
| 2 | 50.04 ± 3.12 | 44.81 ± 5.09 | 49.73 ± 3.18 | 43.98 ± 4.47 | 82.29 ± 3.53 | 129.95 ± 18.79 | 82.22 ± 3.52 | 131.47 ± 18.99 |
| 3 | 23.32 ± 1.22 | 38.95 ± 2.76 | 23.12 ± 1.38 | 39.53 ± 2.62 | 35.1 6± 0.69 | 11.60 ± 2.34 | 35.05 ± 1.13 | 4.77 ± 3.15 |
| 4 | 12.03 ± 0.96 | 68.52 ± 2.34 | 11.32 ± 0.71 | 70.36 ± 1.99 | 6.96 ± 0.42 | 81.70 ± 2.15 | 21.87 ± 0.89 | 38.94 ± 4.14 |
| 5 | 7.07 ± 0.60 | 81.46 ± 1.72 | 6.39 ± 0.43 | 83.27 ± 1.23 | 3.20 ± 0.28 | 91.58 ± 1.24 | 16.20 ± 1.05 | 54.75 ± 4.18 |
| 6 | 4.32 ± 1.60 | 88.63 ± 4.10 | 4.00 ± 0.27 | 89.55 ± 0.42 | 1.77 ± 0.27 | 95.32 ± 1.00 | 14.83 ± 0.86 | 58.55 ± 4.12 |
However, in the ICM method, the WM ratio decreased rapidly at the beginning and then decreased more slowly (Figure 10). The best setting for segmenting the WM and non-WM tissue that achieves a closer WM ratio to the measured values in the literature as well as the minimum RE with a noise reduction guarantee would be ICM3-FA.
Average WM ratio (with respect to total brain volume) versus the number of clusters for Otsu’s, K-means, EM, and ICM methods when FA images are employed after removing CSF tissues. (CSF, cerebrospinal fluid; WM, white matter, FA, fractional anisotropy).
5. Discussion
The segmentation of DTI images of the brain into WM, GM, and CSF with acceptable results is subjected to many factors. The most important issue of brain segmentation from DTI images is the selection of suitable scalar indexes that best describe the required tissue in the images. Specifying the suitable clustering method and the suitable number of clusters of the selected method are other factors that significantly affect the segmentation process. The selection of the recommended segmentation setting is based on five factors: (a) the tissue ratio with respect to the total brain volume compared to the reference model, (b) the RE of a tissue with respect to the reference model, (c) a guarantee of artefact reduction, (d) a low computational cost, and (e) the selection (for MD and FA images) or elimination (for DV images) of one cluster only to support the automatic function.
Four clustering methods, Otsu’s, K-means, EM, and ICM, are used for CSF/non-CSF tissue segmentation using both MD images and DV images as these images’ scalar indices reflect the relative amount of water content in tissues. Regions within MD-based clustering maps that are most likely to be considered CSF regions are assumed to occupy only one cluster in these maps (to enable the automatic segmentation process); however, for DV-based clustering maps, all clusters are considered CSF regions except one cluster that represents non-CSF regions. The computational cost for the ICM method is much higher than Otsu’s, K-means, and EM methods. However, the ICM method would guarantee the elimination of any existing noise in data; thus, the recommended setting for CSF segmentation is when the ICM method is used with two clusters within DV images to build a clustering map (ICM2-DV).
The same four clustering methods are used for WM/non-WM tissue segmentation using FA images, as these images’ scalar indices reflect the relative amount of tissue anisotropy. Regions within FA-based clustering maps that are the most likely to be considered WM regions are assumed to occupy only one cluster in these maps, where other clusters are considered non-WM regions. The best setting for segmenting WM and non-WM tissues would be ICM3-FA. The EM3-FA is the second-best method to achieve the second smaller RE; however, this RE is larger than ICM3-FA (about 240%), which makes ICM3-FA the best choice.
Removing CSF regions from the FA images before applying the clustering algorithms did not significantly affect the results. However, it reduces the opportunity of overlapping between CSF and other non-CSF tissues, as FA images represent rational quantities but the MD and the DV images represent non-rational quantities. One important factor should be taken into consideration when using ICM with FA images: the number of iterations should be sufficiently large (more like 30 iterations) to obtain saturated clustering maps.
Finally, it is possible to separate brain components with less segmentation error and a lower computational cost by employing DV images in segmenting CSF/non-CSF components using the ICM method with two clusters (ICM2-DV) in which the foreground cluster represents CSF regions and by employing FA images in segmenting WM/non-WM components using the ICM method with three clusters (ICM3-FA) in which only one cluster represents WM regions. The removal of CSF before the WM/non-WM segmentation process will minimize the overlap between CSF and non-CSF tissues. The volume ratios of the produced output with respect to the total brain size are 16.7% ± 3.53% for CSF, 35.05% ± 1.13% for WM, and 48.2% ± 2.88% for GM; these results are close to the ratios reported in the literature (1-7) (13% for CSF, 37% for WM, and 50% for GM).
Supplements
Supplementary material(s) is available at below link: http://iranjradiol.com/?page=download&file_id=56267
Acknowledgements
References
-
1.
Kandel ER, Schwartz JH, Jessell TM. Principles of Neural Science. 4. New York: McGraw-Hill Medical; 2000. p. 1227-46.
-
2.
Mortamet B, Zeng D, Gerig G, Prastawa M, Bullitt E. Effects of healthy aging measured by intracranial compartment volumes using a designed MR brain database. Med Image Comput Comput Assist Interv. 2005;8(Pt 1):383-91. [PubMed ID: 16685869].
-
3.
Gur RC, Gunning-Dixon F, Bilker WB, Gur RE. Sex differences in temporo-limbic and frontal brain volumes of healthy adults. Cereb Cortex. 2002;12(9):998-1003. [PubMed ID: 12183399].
-
4.
Sidaros A, Engberg AW, Sidaros K, Liptrot MG, Herning M, Petersen P, et al. Diffusion tensor imaging during recovery from severe traumatic brain injury and relation to clinical outcome: a longitudinal study. Brain. 2008;131(Pt 2):559-72. [PubMed ID: 18083753]. https://doi.org/10.1093/brain/awm294.
-
5.
Holtmannspotter M, Peters N, Opherk C, Martin D, Herzog J, Bruckmann H, et al. Diffusion magnetic resonance histograms as a surrogate marker and predictor of disease progression in CADASIL: a two-year follow-up study. Stroke. 2005;36(12):2559-65. [PubMed ID: 16269644]. https://doi.org/10.1161/01.STR.0000189696.70989.a4.
-
6.
Albrecht J, Dellani PR, Muller MJ, Schermuly I, Beck M, Stoeter P, et al. Voxel based analyses of diffusion tensor imaging in Fabry disease. J Neurol Neurosurg Psychiatry. 2007;78(9):964-9. [PubMed ID: 17449543]. https://doi.org/10.1136/jnnp.2006.112987.
-
7.
Concha L, Gross DW, Beaulieu C. Diffusion tensor tractography of the limbic system. AJNR Am J Neuroradiol. 2005;26(9):2267-74. [PubMed ID: 16219832].
-
8.
Bomans M, Hohne KH, Tiede U, Riemer M. 3-D segmentation of MR images of the head for 3-D display. IEEE Trans Med Imaging. 1990;9(2):177-83. [PubMed ID: 18222762]. https://doi.org/10.1109/42.56342.
-
9.
Westbrook C, Roth CK. MRI in Practice. United States: John Wiley and Sons; 2013.
-
10.
Scampini J. Introduction to computed tomography (CT) medical imaging. Maxim Integrated Products; 2014. Available from: https://www.maximintegrated.com/en/app-notes/index.mvp/id/4682.
-
11.
Mori S. Introduction to diffusion tensor imaging. USA: Elsevier; 2007.
-
12.
Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys J. 1994;66(1):259-67. https://doi.org/10.1016/s0006-3495(94)80775-1.
-
13.
Liu T, Li H, Wong K, Tarokh A, Guo L, Wong ST. Brain tissue segmentation based on DTI data. Neuroimage. 2007;38(1):114-23. [PubMed ID: 17804258]. https://doi.org/10.1016/j.neuroimage.2007.07.002.
-
14.
Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J Magn Reson B. 1996;111(3):209-19. [PubMed ID: 8661285].
-
15.
Vilanova A, Zhang S, Kindlmann G, Laidlaw D. An introduction to visualization of diffusion tensor imaging and its applications. Visual Process Tensor Fields. 2006:121-53.
-
16.
Zarei M, Johansen-Berg H, Matthews PM. Diffusion tensor imaging and tractography in clinical neuro sciences. Iran J Radiol. 2003;1(2):45-52.
-
17.
El-Aff IAI. Extraction of Human Heart Conduction Network from Diffusion Tensor MRI.In: Hierlemann A, editor. The 7th IASTED International Conference on Biomedical Engineering. 2010; Anaheim, CA. Acta Press; p. 217-22.
-
18.
El-Aff I, editor. Human brain tissues segmentation based on DTI data. 11th International Conference on Information Science, Signal Processing and their Applications (ISSPA). 2012; Montreal, QC. IEEE; p. 876-81.
-
19.
Stark DD, Bradley WG. Magnetic Resonance Imaging. USA: Mosby; 1999.
-
20.
Lufkin RB. The MRI Manual. USA: Mosby; 1998.
-
21.
Khotanlou H, Colliot O, Atif J, Bloch I. 3D brain tumor segmentation in MRI using fuzzy classification, symmetry analysis and spatially constrained deformable models. Fuzzy Sets Sys. 2009;160(10):1457-73.
-
22.
Dubey RB, Hanmandlu M, Gupta SK, Gupta SK. The brain MR Image segmentation techniques and use of diagnostic packages. Acad Radiol. 2010;17(5):658-71. [PubMed ID: 20211569]. https://doi.org/10.1016/j.acra.2009.12.017.
-
23.
Portela NM, Cavalcanti GDC, Ren TI. Semi-supervised clustering for MR brain image segmentation. Expert Sys Appl. 2014;41(4):1492-7. https://doi.org/10.1016/j.eswa.2013.08.046.
-
24.
Clarke LP, Velthuizen RP, Camacho MA. MRI Segmentation: Methods and Applications. Magnet Reson Imaging. 1995;13:343–68.
-
25.
Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans Med Imaging. 2001;20(1):45-57. [PubMed ID: 11293691]. https://doi.org/10.1109/42.906424.
-
26.
Chen T, Huang TS, editors. Region Based Hidden Markov Random Field Model for Brain MR Image Segmentation. The Second World Enformatika Conference. 2005; Istanbul, Turkey.
-
27.
Perez P. Markov random fields and images. IRISA; 1998. 31 p.
-
28.
Demirkaya O, Asyali MK, Sahoo PK. Image Processing with MATLAB: Application in Medicine and Biology. USA: CRC Press; 2009.
-
29.
Otsu N. A threshold selection method from gray-level histograms. IEEE Trans Sys Man Cyber. 1979;9:62-6.
-
30.
Wagsta K, Cardie C, Rogers S, Schroedl S. Constrained K-means Clustering with Background Knowledge. Proceedings of the Eighteenth International Conference on Machine Learning. 2001; San Francisco, CA. Morgan Kaufmann Publishers; p. 577-84.
-
31.
Dempster AP, Laird NM, Rubin Maximum DB. Likelihood from Incomplete Data via the EM Algorithm. J R Stat Soc, B. 1977;39:1-38.
-
32.
Wen Y, He L, von Deneen KM, Lu Y. Brain tissue classification based on DTI using an improved fuzzy C-means algorithm with spatial constraints. Magn Reson Imaging. 2013;31(9):1623-30. [PubMed ID: 23891435]. https://doi.org/10.1016/j.mri.2013.05.007.