1. Background
Brain disease is one of the most common diseases that threatens human health and is one of the hottest researches in the medical community and profession. Medical imaging is an essential tool for diagnosis, understanding and treatment of various diseases, including cancer. A vast majority of medical studies and diagnoses are carried out using Magnetic resonance imaging (MRI), positron radiation tomography and computed tomography (CT) scan. MRI is an important experimental investigation technique used for screening abnormal changes in tissues and organs (1). Among the available medical images, MRI images are of higher quality, and unlike some other imaging techniques that use ionizing radiation, MRI makes use of strong electromagnetic waves or radio frequencies; therefore, this imaging method is less harmful, since this imaging technique is one of the most widely used methods in medical science (2).
Diagnosis of brain disease requires a high resolution brain MRI. MRI images have a multidimensional nature and can provide accurate information about the disease (2).
In MRI, by applying an external field (B0), the atomic cores of the body tissues are placed along this magnetic field. At this time, if a radio frequency (RF pulse) is applied at a specific frequency and a particular angle to a patient, the energy level of spins in various tissues of the body will change. For this purpose, firstly, spins of the desired tissues, such as the brain or heart are placed under a strong magnetic force, so that all spins are aligned with the applied field. Then an external radio frequency with appropriate frequency is applied. Spins change their direction based on the RF radio frequency, and their energy level will change. In the absence of this radio frequency, the spins release energy. By making use of MRI, the signal of released energy can be measured, and it can be employed to provide imaging of various body tissues (3, 4).
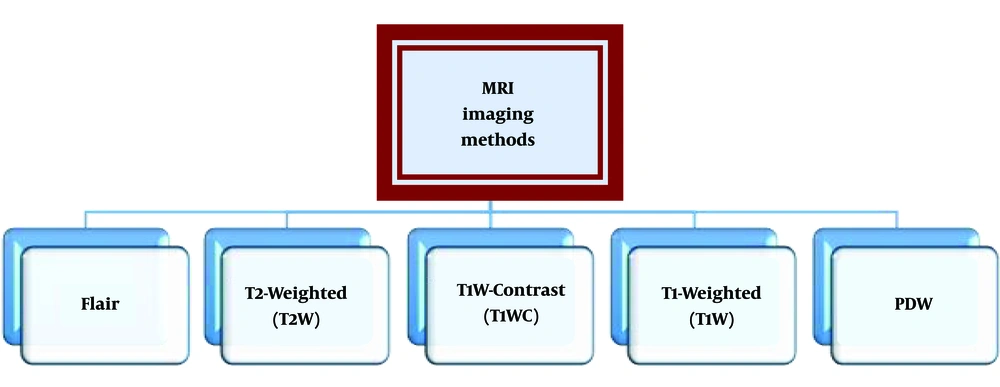
The received signal and signal damping time constant provide important information about the molecular structure of the body. The amplitude of the signal corresponds to the density of the hydrogen atom in one part of the body. The damping time constant T1 weighted determines long relaxation time and the damping time constant T2 weighted specifies the transverse relaxation time of the type of molecule to which the hydrogen atom is bonded. In MRI images, the brightness of each area in the image indicates the size of one of the mentioned parameters. This is evident because this method has the ability to differentiate in atomic level and is one of the most accurate imaging methods (3, 4). Figure 1 shows the imaging techniques.
Figure 1.
Different types of imaging techniques (Flair, fluid-attenuated inversion recovery; PDW, proton-density-weighted)
2. Objectives
The main objective of this research is developing a precise segmentation algorithm for noisy MRI images. The main focus is on a fuzzy clustering method based on evolutionary processing, in order to accurately segment the magnetic resonance images contaminated by different levels of noise.
3. Materials and Methods
Use of intelligent algorithms to diagnose human disease based on medical imaging methods, namely computer-aided diagnosis (CADx) systems contributes significantly to the radiologists' decision-making process. The purpose of these systems is to minimize the efforts needed to investigate the lesion, and to reduce the number of false positive factors along with the cost of treatment (5). Computer-aided detection (CAD) systems for analyzing MRI images exist in the literature (6, 7).
3.1. Image Segmentation Techniques
One of the intelligent methods in analyzing images is the use of segmentation algorithms, which can be considered as a suitable approach in diagnosing and analyzing brain images. Image segmentation is widely used in the processing of different image applications; including clinical applications and medical research. The goal is to split the image into different regions, depending on several criteria.
Medical image segmentation is carried out with the aim of extracting features, measuring different parts of the image, categorizing image pixels into anatomical regions such as bones, muscles and blood vessels, as well as categorizing pixels into pathologic regions such as cancer, tissue abnormalities and multiple sclerosis.
Various methods have been used for MRI image segmentation. Some methods depend on edge and are intended to identify the target boundaries. These methods create closed areas in images, and often fall into false and fake edges, which makes their performance unpredictable. Area-dependent methods extract similar areas based on predefined criterion. This criterion can be related to similar brightness levels, similar texture, uniformity or sharpness in the image. Area growth technique is one of these methods. Pixel-dependent methods perform segmentation according to the brightness of the image, so they are also referred to as light-dependent methods. They include thresholds, K-Means clustering and fuzzy clustering techniques. Statistical segmentation technique is another type of MRI image segmentation technique that considers image statistical properties, such as the distribution of image brightness probabilities. The statistical methods assign the label of each cluster to the corresponding pixel and perform the segmentation of the image with the aid of estimation of the brightness functions. Methods such as the Markov random model are also among these methods (8).
Among the segmentation methods, fuzzy clustering based methods are of higher accuracy. Fuzzy c-means clustering algorithm (FCM) has been widely used for this purpose (6-12). The main motive of this algorithm is segmenting the image into several clusters by minimizing a distance metric between the pixels and the centers of the clusters. The main drawback of FCM is its sensitivity to the noise. So, sometimes, factors such as the internal noise of the MRI imaging device may result in wrong segmentation and hence incorrect diagnosis of the disease in brain images (10).
Some methods are introduced to eliminate noise from MRI images before applying segmentation algorithms on them. Some of them are anisotropic diffusion filter (ADF) (3), wavelet (13), non-local means (NLM) (14), and independent component analysis (15). ADF is the most commonly used noise elimination method in MR images for segmentation of brain images. Skull stripping is another important step in processing for analyzing MR images. Skull stripping is the process of identifying and eliminating non-cerebral tissues such as the skull, skin and other soft tissues of the brain (5).
Several efforts have been performed to make FCM robust against noise. For example Arora and Pandey have mix FCM by a fuzzy support vector machine (SVM) in (9). They have used image spatial information for introducing a noise adaptive FCM algorithm for MRI images segmentation. Xiao and Tong (10) have also shown that combining FCM and SVM can produce good application presentation. On the other hand, Venu has evaluted using Guassian kernals for FCM algorithm (11) and Lan et al. have used Kerneled FCM combining image filtering method for this purpose (12).
Applying metaheuristic on FCM is another way for making a robust algorithm against noise. Jansi and Subashini have tested it (16). Ghassabeh et al. have used an improved version of FCM (IFCM) for overcoming FCM algorithm weakness by introducing two new parameters for considering pixel’s neighborhood and location effect called λ and ζ (1). Then, they tried to optimize IFCM using genetic algorithm.
3.2. The Proposed Method (PSO-IFCM)
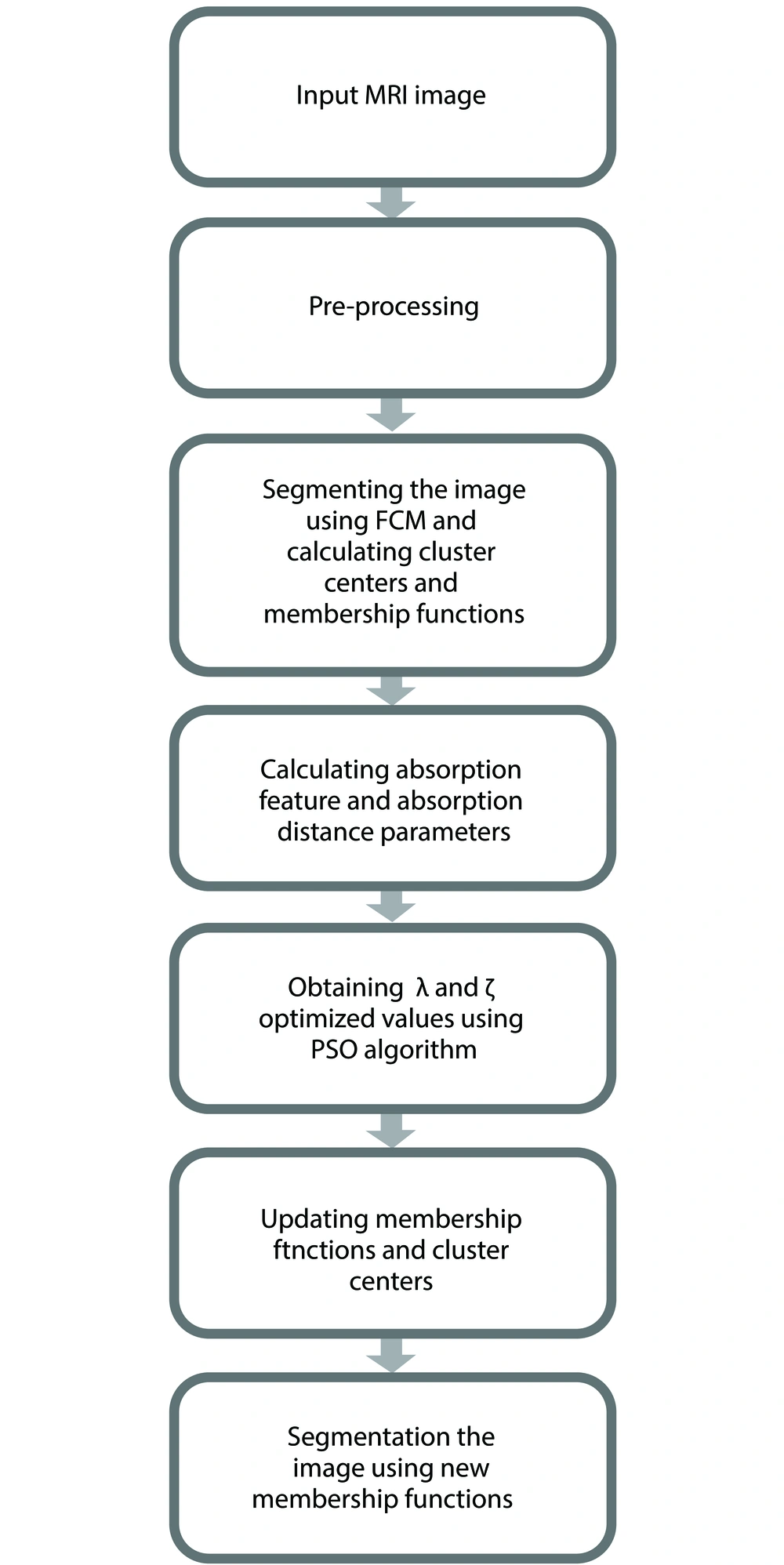
In this paper, a new method for reducing FCM sensitivity to noise is proposed. In this way, first the IFCM algorithm (1) is applied to MRI images. In the next step, PSO algorithm is used to optimize the parameters. Figure 2 shows the flowchart of the proposed algorithm.
Figure 2.
Flowchart of the proposed algorithm (PSO, particle swarm optimization)
The MRI image or its intentionally noise-added version is used as the input of the algorithm. First, some pre-processing methods as well as skull stripping are applied on it to prepare it for other steps. Original FCM algorithm is performed over it to initially segment it into its four cluster. Absorb feature and absorb distance parameters and their related λ and ζ coefficients are calculated. These coefficients are fed into PSO algorithm to find their optimized values.
PSO proposed by Eberhart et al. (17), is an iteratively computational method for solving the optimization problem. Recently it has gained more attention and has been more used for several applications (18, 19).
In the PSO, each particle represents a solution to the problem and moves around a multi-dimensional search space at the initial velocity assigned to the particles. During the flight, each particle adapts its location to its experience and experience of its neighboring particles, and uses the best place it encounters with itself and its neighbors, and then the particles move towards the best solution, which is the particle that is more fitted. The performance of each particle is measured in terms of fitness function. This act is repeated so as to achieve convergence.
The membership functions and cluster centers of the previously performed FCM algorithm is updated using the optimized values of PSO step. Finally segmenting the MR image using updated FCM will generate the output of the algorithm.
3.3. Data Collection
Simulated brain database (SBD), as a realistic MRI data volume, is used for validation of different computer-aided and quantitative techniques in the analysis of medical images. In this paper, a simulated MRI image with the weight of T1 (181 × 217 × 181), is taken from BrainWeb image database (20, 21). In order to see the algorithms’ performance, some Gaussian noise is added to it. Segments 90 to 100 of brain images in the presence of different noises were selected for segmentation using the proposed algorithms, and performance of algorithms in different noises and segments was investigated.
3.4. Segmentation Evaluation Methods
There are several indicators for evaluating the segmentation techniques and quality of algorithms. In this research, a standard metric that was more accurate was used to measure the performance of the proposed algorithms. The Dice index or overlap ratio was used to compare the similarity between two sets of samples that were similar to each other and were defined as:
Where, in our case, S1 and S2, are image pixels segmented with suggested algorithm and reference image pixels, respectively. When the segmentation image results completely match the non-noisy reference image, the value of this criterion will be 100%. On the other hand, when there is no matching between the two images, the value of this criterion will be 0%.
4. Results
To measure the performance of the proposed method, T1W brain images were used. During the experiments, for comparing the proposed algorithms, standard FCM clustering algorithm, Gaussian kernel FCM, and genetic algorithm improver fuzzy c-mean (GA-IFCM) were performed also. Following this, the results of each of the optimized and improved FCM clustering algorithms were compared.
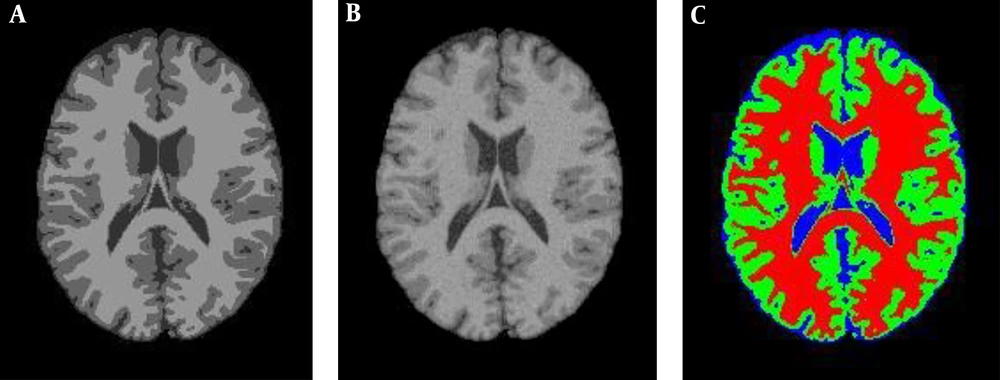
Figure 3A is the 90th segment of the simulated MR image with the weight of T1, and Figure 3B illustrates the image in the presence of 5% noise, and the segmentation operation is shown in Figure 3C, which is the result of applying the proposed PSO-IFCM algorithm. Each brain MR image can have four clusters namely, background (BGND), gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF) (1). Every algorithm that extracts these tissues by higher precision has a better performance. To evaluate the accuracy of segmentation, Dice coefficient (DC) described in equation 1 is used. The results of this section are illustrated in Table 1.
Figure 3.
An example of the implementing the proposed algorithm
Table 1.Accuracy Results of MR Image Segmentation for the 90th Cut
| Brain tissues | Metric, % | FCM | KFCM | GA-IFCM | PSO-IFCM |
|---|---|---|---|---|---|
| WM | DC | 98.1745 | 98.1745 | 98.605 | 98.6099 |
| GM | DC | 96.0919 | 97.0543 | 97.821 | 97.8232 |
| CSF | DC | 97.3572 | 98.6455 | 99.132 | 99.1318 |
| BGND | DC | 99.4399 | 99.7556 | 99.916 | 99.9185 |
| Average | DC | 97.7659 | 98.4075 | 98.868 | 98.8708 |
Abbreviations: BGND, background; CSF, cerebrospinal fluid; DC, Dice coefficient; FCM, fuzzy c-means; GA-IFCM, genetic algorithm-improver fuzzy c-mean; GM, gray matter; KFCM, kernel FCM; PSO-IFCM, particle swarm optimization-improver fuzzy c-mean; WM, white matter
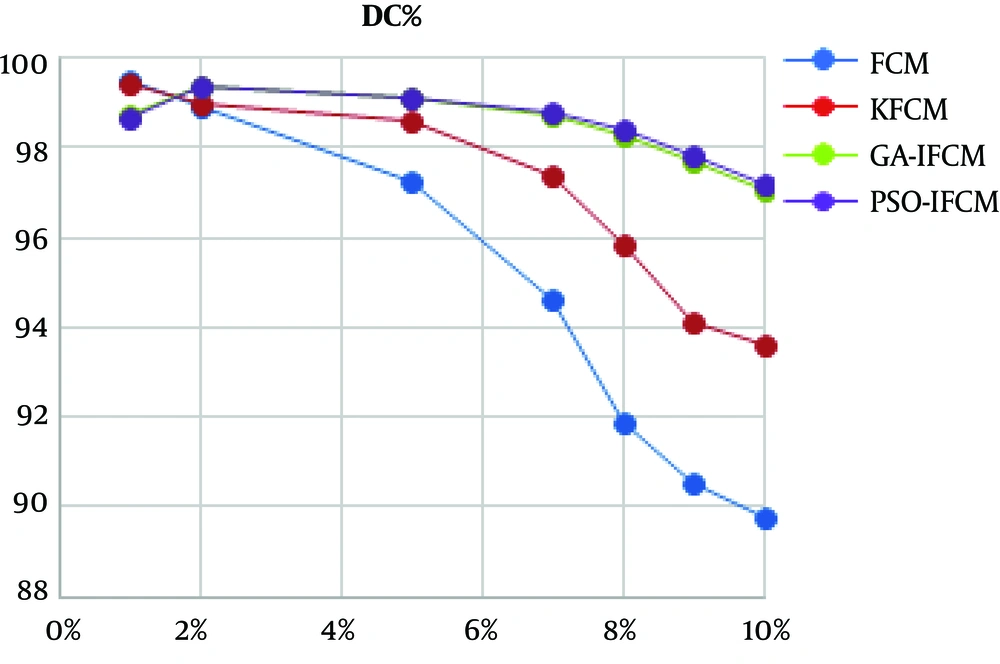
In order to see the performance of the proposed algorithm in noisy images, all algorithms were applied over MR images contaminated by different levels of noise. Figure 4 shows a continuous chart of Dice coefficient for different noises at 100th cut of brain MR image.
Figure 4.
Continuous chart of DC for different noises at 100th cut from brain MR image (DC, Dice coefficient; GA-IFCM, genetic algorithm-improver fuzzy c-mean; FCM, fuzzy c-means; KFCM, kernel FCM; PSO-IFCM, particle swarm optimization-improver fuzzy c-mean)
5. Discussion
The advantage of basic FCM clustering algorithm in segmenting MR images is shown the literature. As shown in Table 1, FCM and all its derivations, including PSO-IFCM as the proposed method, have acceptable segmental accuracy in low noise images. All the algorithms have above 97% accuracy in segmenting this image. Figure 3 shows the algorithm performances in noisy images. The horizontal axis is percentage of Gaussian noise added to 100th cut MR image. The vertical axis shows the DC value of segmentation. As shown, with the increase of noise, the accuracy of basic FCM and kernel FCM (KFCM) algorithms drops. But enhanced FCM algorithms such as GA-IFCM and PSO-IFCM are more robust against noise augmentation. In high noises, GA-IFCM and PSO-IFCM algorithms function similarly, and the accuracy of these algorithms is very close to each other.
In conclusion, according to the importance of analyzing magnetic resonance images of the brain, a new segmentation method is proposed in this paper named PSO-IFCM. By applying the proposed method on real images in the presence of different levels of noise, the advantages over the existing methods is shown. Fuzzy clustering method has a higher accuracy and processing speed than classical methods. The results of applying standard FCM algorithm on noisy brain MRI imagery indicate that is has a desirable accuracy for very low noise. For moderate noise, the KFCM algorithm has a desirable accuracy. For high noise, the GA-IFCM and PSO-IFCM algorithms are well-suited. Main limitation of using metaheuristic algorithms such as GA and PSO is their consumed time. As the segmentation methods are used offline, no processing time comparison between algorithms is done in this paper.
