https://doi.org/10.5812/jjhr.12028

A Comparison of Stress Distribution Around Dental Implants in Three Models of Arch Form to Replace Six Anterior Teeth of Maxilla using the Finite Element Analysis (FEA) Method

authors:

avatar Mahmoud Jahangirnezhad 1 , avatar Hojatollah Yousefimanesh 1 , avatar Maryam Zarei 1 , * , avatar Iman Ivaz 2

Department of Periodontics, School of Dental Medicine, Ahvaz Jundishapur University of Medical Sciences, Ahvaz, IR Iran
School of Dental Medicine, Ahvaz Jundishapur University of Medical Sciense, Ahvaz, IR Iran
Jentashapir Journal of Health Research: Vol.8, issue 6; e12028
published online: August 31, 2017
article type: Research Article
received: April 24, 2017
accepted: July 23, 2017

how to cite: Jahangirnezhad M, Yousefimanesh H, Zarei M, Ivaz I. A Comparison of Stress Distribution Around Dental Implants in Three Models of Arch Form to Replace Six Anterior Teeth of Maxilla using the Finite Element Analysis (FEA) Method. Jentashapir J Cell Mol Biol. 2017;8(6):e12028. https://doi.org/10.5812/jjhr.12028.

Abstract

Background and Objectives:

Dental implant is a method to replace missed teeth, and especially for aesthetic it is important to replace the missing anterior teeth. Thus, in this study, for replacement of 6 maxillary anterior teeth by finite element analysis (FEA) method, stress distribution around implants in 3 models of maxillary arch were compared.

Methods:

In this in-vitro study, a toothless patient’s CBCT was used to create a model for maxillary anterior teeth. The ITI dental implant with a 10-mm length and 4.1-mm diameter was used to replace central and canine teeth.
Using the ABAQUS software, simulation was performed for reconstruction of 6 maxillary anterior teeth, so that 2 implants were placed on both sides of the canine tooth region (model A); 2 implants on both sides of the canine tooth region and another on one side of the central region (model B); as well as 2 implants on both sides of the canine tooth region and 2 implants in the central area (model C). These models were repeated in the triple square, ovoid, and tapering arches. In all cases, a 100-N force with a 30-degree angle was imposed buccolingually to each veneer to simulate the functional forces. Data were then analyzed by the finite analysis software, ABAQUS.

Results:

By applying a 100-N force under a 30-degree angle, along with the increase of implants number, von Mises stress in the models was reduced. In a comparison of models A in each maxillary arch, the stress created in the cortical and cancellous bones in the square arch was less than ovoid and tapering arches. In addition, in a comparison between models B and C in the 3 maxillary arches, stress in the cortical and cancellous bones in the tapering arch was less than square and ovoid arches. The stress created in implants and cortical and cancellous bones in model C was less than the A and B models.

Conclusions:

The results show that unlike 2- or 3-implant models, in the 4-implant model, the stress distribution was reduced in cortical and cancellous bones.

1. Background

Tooth loss can be single-tooth, partial and/or becoming completely toothless. The teeth are missed due to decay and endodontic treatments and fracture. Replacement of these teeth to maintain the shape of the arch and the proper occlusion is important. One of the areas of the patient’s jaw, which may suffer from edentulous due to decay, the failure of endodontic treatment and fractures caused by trauma and periodontal problems, is the six maxillary incisors. This area has been a very important area in terms of aesthetic and its reconstruction causes problems. A perfect solution in this area is the use of dental implant and implant-supported fixed denture. For many years, the most common method for replacing missed anterior teeth was making multiple-unit fixed bridges. This type of restoration can return the construction and the patient to natural conditions within 1 or 2 weeks in terms of performance, comfort, beauty and speech, and the shape of the tissue (1).

The fundamental problem with this type of treatment is the limited time for repair of performance problems, especially problems created for the abutments. Basic dental decay and endodontic failure of the abutments is among the main reasons for the failure of the prosthesis. The risk of periodontal problems, such as bone loss in abutment tooth is also high. Undesirable results in the conventional constant therapy do not only lead to the need of prosthesis for replacement, but also abutment will be missed and the bridge is longer (2).

In terms of the acceptability of treatment, soft tissue-supported removable partial denture is one of the weakest dental treatments. The low survival percentage, risk for tooth health, and adjacent tissues of partial denture are some of the undesirable characteristics (3).

Dental implants are known as the most predictable way to replace missing teeth methods. Because of improvements observed in implant treatment and excellent long-term results, the use of implants takes place for reconstruction of partial edentulous areas (4).

The shape of the premaxillary arch influences the fixed prosthetics treatment plan of the edentulous anterior maxillary. Three of the specific shapes of the arches are ovoid, square, and tapering. As a result of bone loss, the edentulous ridge arch shape may be different from the toothed arch shape. The shape of the patient’s arch is determined by final positions of premaxillary crowns and 9 of the rest ridge arch shapes. The shape of the anterior maxillary dental arch is determined by the distance between the 2 horizontal lines. The first line is drawn from the incisal edge of the canine to the incisal edge of the canine. The second line is drawn parallel to the first line and along the anterior facial position.

When the distance of these 2 lines is less than 8 mm, there is a square-shaped dental arch. When there is a distance between the 2 lines of 8 to 12 mm, there is an ovoid-shaped dental arch that is the most common shape that can be seen. When the distance between the 2 lines is over 12 mm, the dental arch is tapering-shaped.

In the square arch, the 2 implants in canines may be enough to replace the 6 anterior teeth. If the final position of the teeth is oval-shaped, at least 3 implants should be placed in the premaxillary: One implant in the position of canines on both sides, and the third implant preferably in the central location. Tapering-shaped arch applies the most force on the anterior implants; for this same reason, for the replacement of 6 anterior teeth, 4 implants should be considered. Bilateral canines and central incisors are the best areas (5).

Dimensions of oval and square dental arches do not provide and inter-implant space for placement more than four implants. The larger inter-implant distance is found mainly in the tapering-shaped arc. As a result, typically more than 4 dental implants are not used to replace the 6 anterior teeth, even when the bone implantation makes the shape of the remaining ridge more appropriate (6). The existing methods for understanding these items can often be done through clinical measures, yet given that it was not morally feasible and considering that the risks are unclear, treatments were simulated in the form of laboratories and risks were investigated (7).

In the past 2 decades, Finite element analysis has served as an appropriate and useful tool for predicting the effects of stress on the implant and the bone around it. The main problem in the simulation of mechanical behavior of dental implants is modeling of bone tissue and responses to the applied mechanical forces. Detailed decisions should be adopted for the realization of modeling and analysis (8).

According to what was said, in all types of dental arches, a fixed number of implants are used. In this research project, using the finite element method, the researchers investigated the effect of dental arches on the number of implants by evaluating stresses around the dental implants to replace the 6 anterior teeth.

2. Methods

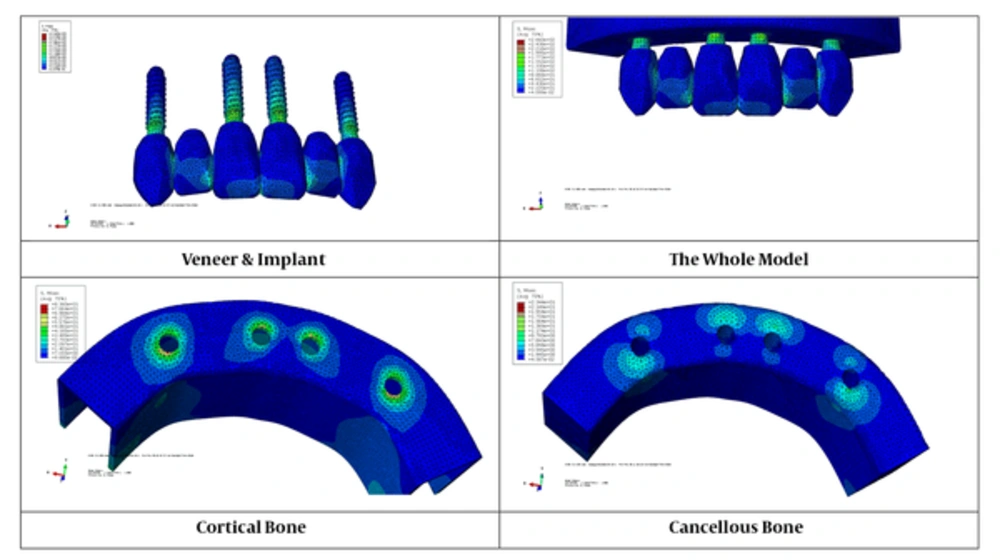
In this in vitro study, a 50-year-old toothless patient’s CBCT was used in order to build a 3-dimensional model of the anterior maxillary teeth (9). The CBCT data were transferred to the MATERIALISE MIMICS v10.01 modeling software, and the exact and 3D maxillary contour was designed using this software. Based on the Lekholm and Zarb classification, the maxillary bone model was chosen. The type 2 bone (trabecular bone modeled as a solid structure in the cortical bone) that included a cancellous bone in the center with 1-mm circumambient cortical bone (10) was simulated (11).

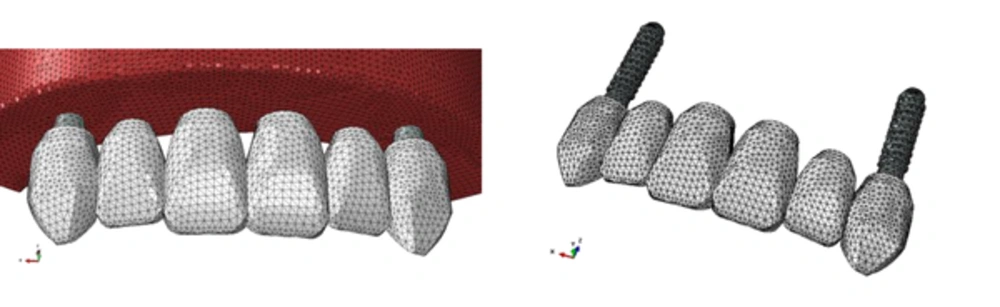
Models created with the stl format (output format of the software) were transferred to the Rapidform and Geomagic studio software, where the created meshes were optimized and non-necessary points and fields were removed and an editable 3D volume was prepared. Furthermore, in this study, 2 screw-form dental implants (ITI; Institut Straumann AG, Waldenburg, Switzerland) with 10-mm length and 4.1-diameter were used to replace central and canine teeth (11).

Moreover, cobalt-chromium (Wiron 99; Bego, Bremen, Germany) and feldspathic porcelain were selected for crown metal frame and occlusal surface. The thickness of porcelain and metal was 0.8 to 2 mm and the thickness of the cementum layer was ignored (12). The data were analyzed by the ABAQUS FEA software 6.8 (Simulia Corporation, Velizy-Villacoublay, France). In this software, the models for veneer and implant were designed using available references and manufacturer’s instructions. The thickness of the porcelain and metal used for this study was 8.0 up to 2 mm, and the thickness of the cement layer in the study was ignored (12). The final file was transferred to the Abaqus 6.8 software (Simulia Corporation, Velizy-Villacoublay, France) for finite element analysis. In this software, at first, the teeth veneer model was drawn and created using existing references and the implant model with the use of the catalog of the manufacturing company.

Then, different parts of the jaw consisting of cortical and cancellous bones (obtained from the Mimics software), veneer, and implant (drawn in the environment of the ABAQUS software and with a suitable genus attributed to each of them) were assembled together (13). In all cases, to simulate the functional forces, a 100-N force with a 30-degree angle was buccolingually imposed to each veneer (14, 15). Then, the data were analyzed using the Abaqus Finite Element Application software.

In this study, based on dental arches for reconstruction of 6 maxillary anterior teeth, the researchers simulated 9 models as follows:

In the square arch:

A1 Model: two implants in the area of canines on both sides (Figure 1)

The 3D view of the A1 model
The 3D view of the A1 model
Figure 1.

The 3D view of the A1 model

B1 Model: two implants in the canines’ area on the both sides and another in the central area

C1Model: two implants in the canines’ area and two implants in the central area

In the ovoid arch:

A2 Model: two implants in the area of canines on both sides

B2 Model: two implants in the canines’ area on both sides and another in the central area

C2 Model: two implants in the canines’ area on both sides and two implants in the central area

In the tapering arch:

A3 Model: two implants in the area of the canines on both sides

B3 Model: two implants in the canines’ area on both sides and another in the central area C3 Model: two implants in the canines’ area on both sides and two implants in the central area

3. Results

The stress distribution of von Mises was examined in each of the nine models and in diverse areas. According to the results, in the three models, the stress distribution was nearly similar and only a difference was seen in stress amount.

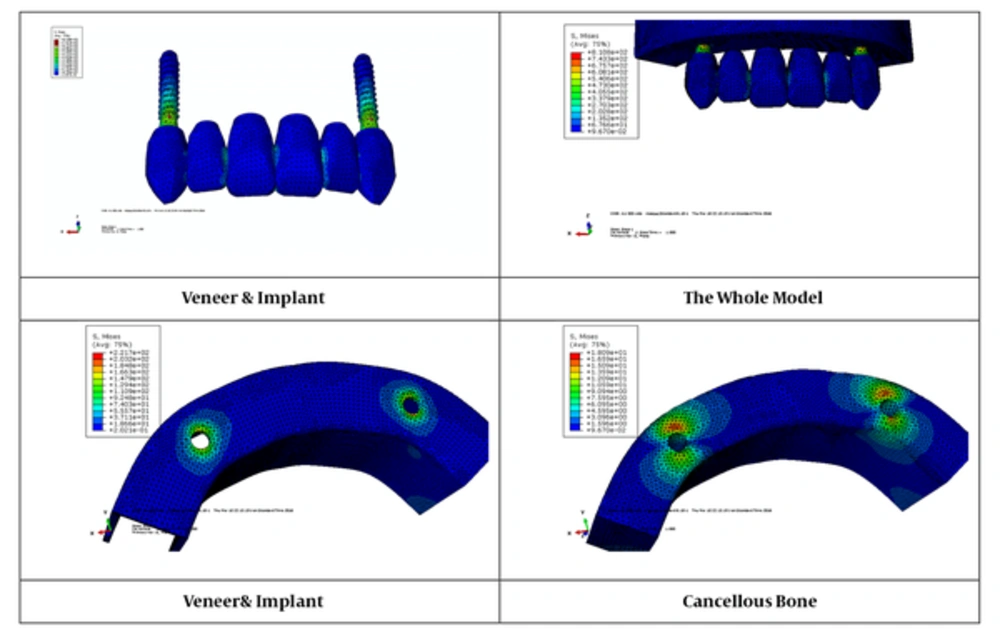
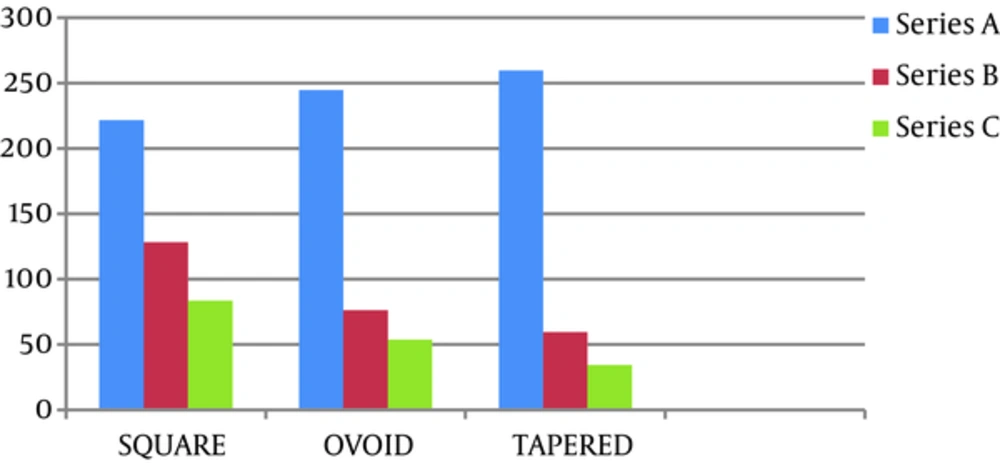
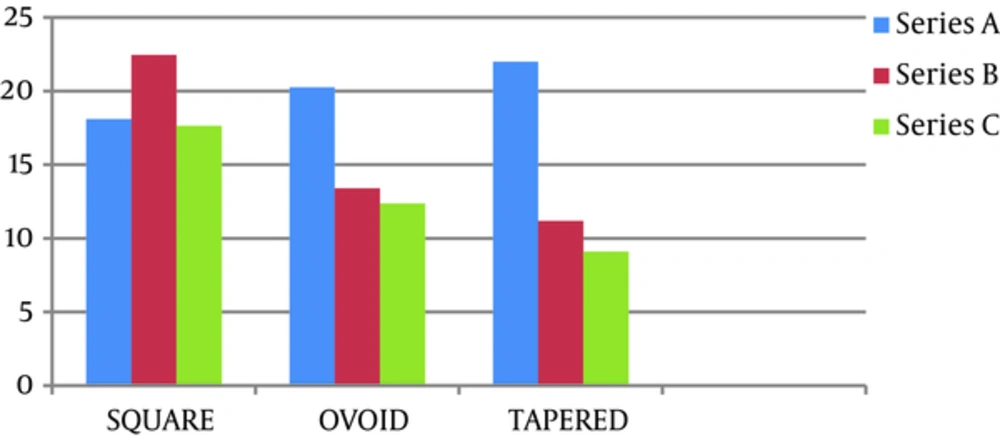
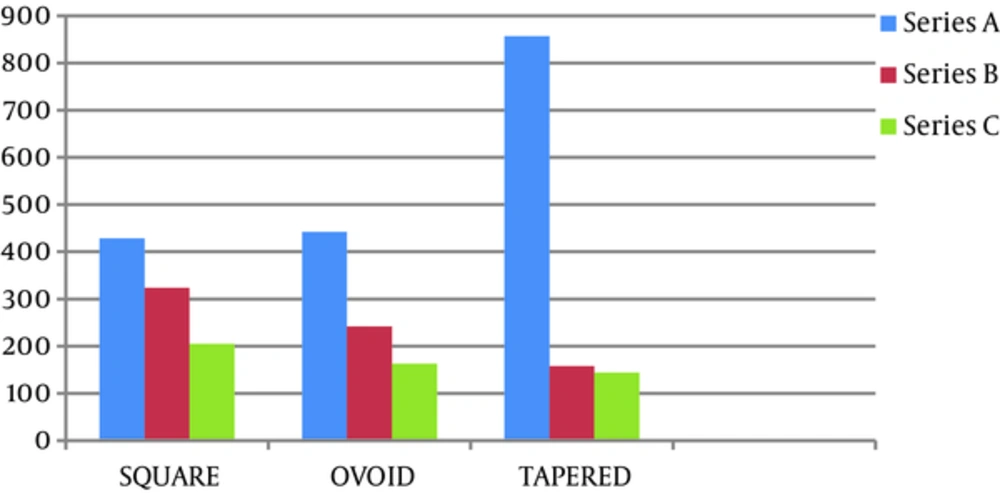
The results showed that after impose of a 100-N force, the stress amount of von Mises in the cortical and cancellous bones around implants under a 30-degree angle in comparison between models A1, B1, and C1 in the square arch in the C1 model was less than all others, and next, respectively B1 and A1 (Figures 2 and 3). Furthermore, in the oval and tapering arches, the results were comparable.

The distribution model of stress in the A1 model
The distribution model of stress in the A1 model
Figure 2.

The distribution model of stress in the A1 model

The distribution model of stress in the B1 model
The distribution model of stress in the B1 model
Figure 3.

The distribution model of stress in the B1 model

A comparison between the two-implant model in the triple arches showed that the amount of stress created in implants and cortical and cancellous bones around them in the square arch (A model) was less than oval (A2 model) and tapering arches (A3 model). Stresses in the oval arch are less than the triangular arch (Figures 2 to 4).

The distribution model of stress in the C1 model
The distribution model of stress in the C1 model
Figure 4.

The distribution model of stress in the C1 model

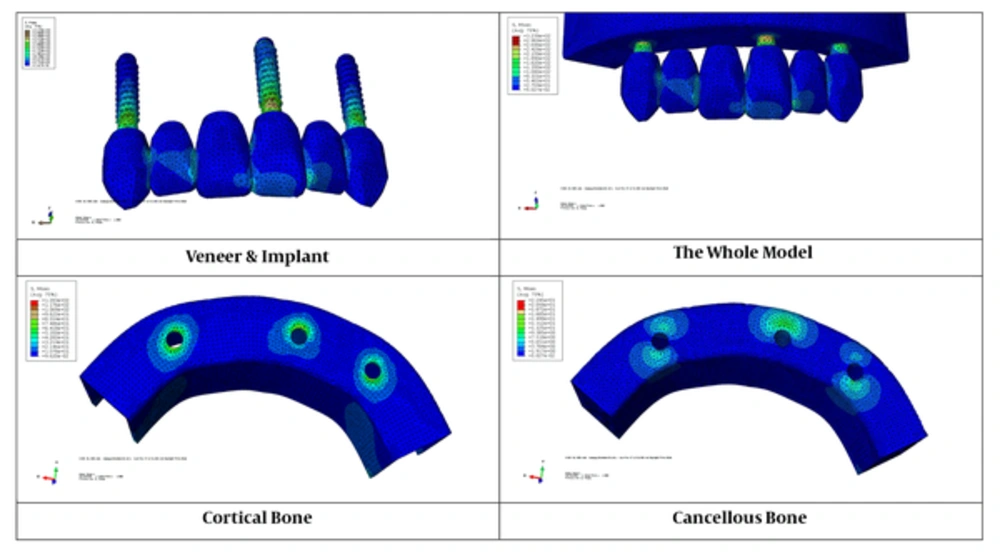
A comparison between the three-implant model in the 3 jaw arches showed that the amount of stress created in the implants and cancellous and cortical bones around them in the triangular arch (B3 model) was less than in the oval (B2 model) and square arches (model B1). In the oval arch, stresses were less than in the square arch (Figures 2 to 4).

A comparison between the 4-implant model in the 3 jaw arches showed that the amount of stress created in the implants and cortical and cancellous bones around them in the triangular arch (C3 model) was less than in the oval (B2 model) and square arches (model B1). In the oval arch, stresses were less than in the square arch (Figures 2 to 4).

Moreover, the amount of stress created around the implants in the cortical bone was more than the cancellous bone (Figures 5 and 6).

A comparative chart of stress created in the cortical bone in various arches
A comparative chart of stress created in the cortical bone in various arches
Figure 5.

A comparative chart of stress created in the cortical bone in various arches

A comparative chart of stress created in cancellous bone in the various arches
A comparative chart of stress created in cancellous bone in the various arches
Figure 6.

A comparative chart of stress created in cancellous bone in the various arches

Furthermore, the figure showed that the greatest amount of stress applied to the implant in these models was in the neck area of the implants, and the stress levels were reduced by moving towards the apical implant (Figures 2 to 4 and 7).

A comparative chart of stress created in the implant in various arches
A comparative chart of stress created in the implant in various arches
Figure 7.

A comparative chart of stress created in the implant in various arches

4. Discussion

The aim of this study was to compare the amount of stress distribution around dental implants to replace the 6 anterior maxillary teeth using the finite element analysis. The finite element analysis is a proven theoretical technique that is used to solve engineering problems and can be an alternative for studies of clinical samples, for which data collection of in vivo data is impossible or scientifically questionable (16). There are some limitations in case of emulating the example by FEA. Dimensions of the substructures were obtained from real clinical samples, and implant size was taken from commercial sources. These cases ensure real geometry of the models of this study. However, in this model, the structures were assumed to be homogenized and isotropic while the contact area between the bone and the implant was considered thoroughly as osteointegrated, which is away from reality (17); they are considered as one of the limitations of this study as in a study by Baghai et al. it was demonstrated that by applying the same force, higher stress values are seen in the bone around the implant with a lower percentage of osteointegration (18). In any case, the results achieved from the finite element analysis only provided a general overview of biomedical aspects in the normal conditions; thus, the results achieved from FEA need to be proved with clinical research.

In this study, a force of 100 N was applied under a 30-degree angle. According to the results obtained in this study, it was shown that whenever the number of implants in different models of the arch of the jaw is increased, the amount of the stress Von Mises created in the implant, veneer, and spongy and cortical bone around implants is reduced and the lowest stress is created by the force of 100 N in a 30-degree angle in the 4-implant triangular jaw arc model. These findings are in contrast with the study conducted by Mahshid et al. They showed that the level of stress in cancellous bone decreases from the 2-implant model to the 4-implant model, yet it increases in the 5-implant model. Furthermore, stress on cortical bone of the end implants in the 2, 3 and 4-implant models were similar. While in the 5-implant model, the amount of stress on the end implants was dramatically higher (19). In another study, Correa et al. assessed the fixed denture restorations-supported three- or four-implant structure, and showed that the failure rate of the 3-implant-supported prosthesis was more. As a result, this type of prosthesis is not structurally recommended, because it does not provide enough support for the occlusal forces (16). Liu et al. investigated the impact of the number of implants on the biomechanical behavior of the implant-supported overdentures. They concluded that the 3 or 4-implant models were more stable than the 2-implant model, and transferred less stress to the bone around the implant (20).

According to the results obtained from the comparison of stress in the cortical and cancellous bones, it was demonstrated that the amount of stress created in the cortical bone around implants in each of the studied models was more than cancellous bone around the same implant, and maximum stress on all the models was accumulated in the crystal area of the bone and the implant. Similar findings were reported in laboratory studies on animals. Hoshaw et al. reported that applying an excessive force to the implants caused an increase in loss of bone in the neck area of the implant and the percentage of bone in the mineralized tissue cortex was reduced (21). Papavasiliou et al. investigated stress distribution around the implant. They showed that stress in the crystal area of the implant in all situations was more than the apical area (22). Tada et al. showed that the utmost stress created with the applied power in models with low density bone was seen in the apex of the implant due to a lower density of bone in the area; thus, this finding was the opposite of the current findings (23). Baumeister et al. expressed that when 2 substances with different modulus of elasticity are placed together without any interstitial substance and one of them is loaded, there is greater increasing stress on the area where they are in contact with each other for the first time. As a result, they showed that the most stress in the place of contact of implants to the bone was seen in the crystal area of the implant (24). The results of this study were consistent with the findings of other studies (21, 25, 26).

According to the values of the Von Mises, it was shown that in any of the models the amount of stress created in Veneer, implants, cortical, and cancellous bones dropped and the lowest stress was applied to cancellous bone in each model. This finding could be due to the very high modulus of elasticity of superstructures and implants than cortical and cancellous bones. As a result, more stress is created in an object that has a higher modulus of elasticity (27).

According to the results obtained from the comparison of 3 models, it was shown that under the same force in model C, the amount of tension created in the implants and spongy and cortical bone around them, was less than the stress created in the A and B models. Moreover, the greatest amount of stress was seen in the mesial area of the implant, at the junction with the pontic. Misch showed that two-pontic implant-supported prosthesis is bent 8 times more than one-pontic implant-supported prosthesis (28). As a result, a greater length of pontic in the A model can be the cause of further stress in this model.

In addition, the amount of tension created in the implants and cortical and cancellous bone around them in A model, was more than tension created in the B model. It seems that the result is due to greater length of the pontic in the A model.

4.1. Conclusions

In conclusion, model C with 4 implants (2 implants in the canine area on both sides and 2 implants in the central region on both sides) and a 4-unit partial denture on the implants is recommended as the proposed treatment plan for the reconstruction of 6-teeth anterior maxillary in each of the 3 jaw arches.

Acknowledgements

References

  • 1.

    Misch CE. Maxillary arch implant considerations: Fixed and overdenture prostheses. In: Misch C, editor. Contemporary Implant dentistry. St Louis: Mosby; 2008. p. 367-71.

  • 2.

    Misch CE. Treatment planning for the edentulous posterior. In: Misch C, editor. Contemporary implant dentistry. St Louis: Mosby; 2008. p. 389-418.

  • 3.

    Adell R, Eriksson B, Lekholm U, Brånemark PI, Jemt T. A long-term follow-up study of osseointegrated implants in the treatment of totally edentulous jaws. Int J Oral Maxillofac Implants. 1990;5(4).

  • 4.

    Adell R, Lekholm U, Rockler B, Branemark PI. A 15-year study of osseointegrated implants in the treatment of the edentulous jaw. Int J Oral Surg. 1981;10(6):387-416. [PubMed ID: 6809663].

  • 5.

    Misch CE. Maxillary arch implant considrations: Fixed and overdenture prostheses. In: Misch C, editor. Contemporary implant dentistry. St Louis: Mosby; 2008. p. 374-7.

  • 6.

    Misch CE. Treatment plans for partially and completely edentulous arches in implant dentistry. In: Misch C, editor. Contemporary implant dentistry. St Louis: Mosby; 2008. p. 406-18.

  • 7.

    Jensen J, Sindet-Pedersen S, Oliver AJ. Varying treatment strategies for reconstruction of maxillary atrophy with implants: results in 98 patients. J Oral Maxillofac Surg. 1994;52(3):210-6. discussion 216-8. [PubMed ID: 8308618].

  • 8.

    Wakabayashi N, Ona M, Suzuki T, Igarashi Y. Nonlinear finite element analyses: advances and challenges in dental applications. J Dent. 2008;36(7):463-71. [PubMed ID: 18455859]. https://doi.org/10.1016/j.jdent.2008.03.010.

  • 9.

    Eskitascioglu G, Usumez A, Sevimay M, Soykan E, Unsal E. The influence of occlusal loading location on stresses transferred to implant-supported prostheses and supporting bone: A three-dimensional finite element study. J Prosthet Dent. 2004;91(2):144-50. [PubMed ID: 14970760]. https://doi.org/10.1016/S0022391303007418.

  • 10.

    Gapski R, Wang HL, Mascarenhas P, Lang NP. Critical review of immediate implant loading. Clin Oral Implants Res. 2003;14(5):515-27. [PubMed ID: 12969355].

  • 11.

    Holmes DC, Loftus JT. Influence of bone quality on stress distribution for endosseous implants. J Oral Implantol. 1997;23(3):104-11. [PubMed ID: 9477847].

  • 12.

    Vojdani M, Sabouri A, Jafari K, Khajehpour S, Farjoud E. Effect of Framework Material on Stress Distribution around Implants using Three-Dimensional Finite Element Analysis. Shahid Beheshti Univ Dent J. 2013;30(4):233-9.

  • 13.

    Lewinstein I, Banks-Sills L, Eliasi R. Finite element analysis of a new system (IL) for supporting an implant-retained cantilever prosthesis. Int J Oral Maxillofac Implants. 1995;10(3):355-66. [PubMed ID: 7615332].

  • 14.

    Bahuguna R, Anand B, Kumar D, Aeran H, Anand V, Gulati M. Evaluation of stress patterns in bone around dental implant for different abutment angulations under axial and oblique loading: A finite element analysis. Natl J Maxillofac Surg. 2013;4(1):46-51. [PubMed ID: 24163552]. https://doi.org/10.4103/0975-5950.117882.

  • 15.

    Jafari K, Vojdani M, Mahdavi F, Heidary H. Finite element analysis of the effect of superstructure materials and loading angle on stress distribution around the implant. J Dent Biomaterials. 2014;1(2):57-62.

  • 16.

    Correa S, Ivancik J, Isaza JF, Naranjo M. Evaluation of the structural behavior of three and four implant-supported fixed prosthetic restorations by finite element analysis. J Prosthodont Res. 2012;56(2):110-9. [PubMed ID: 22104623]. https://doi.org/10.1016/j.jpor.2011.07.001.

  • 17.

    Cochran DL. The scientific basis for and clinical experiences with Straumann implants including the ITI Dental Implant System: a consensus report. Clin Oral Implants Res. 2000;11 Suppl 1:33-58. [PubMed ID: 11168256].

  • 18.

    Baghai Naini R, Nokar S, Borghei SH. A three-dimensional finite element analysis of peri-implant bone stress and strain distributionin All-on-4 design. J Dent Med. 2010;23(2):104-12.

  • 19.

    Mahshid M, Geramy A, Ejlali M, Sedaghat Monfared M, Rezvani Habib Abadi S. Effect of the number of implants on stress distribution of anterior implant-supported fixed prostheses combined with a removable partial denture: a finite element analysis. J Dent (Tehran). 2014;11(3):335-42. [PubMed ID: 25628669].

  • 20.

    Liu J, Pan S, Dong J, Mo Z, Fan Y, Feng H. Influence of implant number on the biomechanical behaviour of mandibular implant-retained/supported overdentures: a three-dimensional finite element analysis. J Dent. 2013;41(3):241-9. [PubMed ID: 23160036]. https://doi.org/10.1016/j.jdent.2012.11.008.

  • 21.

    Hoshaw SJ, Brunski JB, Cochran GVB. Mechanical Loading of Brånemark Implants Affects Interfacial Bone Modeling and Remodeling. Int J Oral Maxillofac Implants. 1994;9(3).

  • 22.

    Papavasiliou G, Kamposiora P, Bayne SC, Felton DA. Three-dimensional finite element analysis of stress-distribution around single tooth implants as a function of bony support, prosthesis type, and loading during function. J Prosthet Dent. 1996;76(6):633-40. [PubMed ID: 8957790].

  • 23.

    Tada S, Stegaroiu R, Kitamura E, Miyakawa O, Kusakari H. Influence of implant design and bone quality on stress/strain distribution in bone around implants: a 3-dimensional finite element analysis. Int J Oral Maxillofac Implants. 2003;18(3):357-68. [PubMed ID: 12814310].

  • 24.

    Baumeister T, Avallone EA. Marks' standard handbook ofmechanical engineers. New York: McGraw-Hill; 1978.

  • 25.

    Duyck J, Ronold HJ, Van Oosterwyck H, Naert I, Vander Sloten J, Ellingsen JE. The influence of static and dynamic loading on marginal bone reactions around osseointegrated implants: an animal experimental study. Clin Oral Implants Res. 2001;12(3):207-18. [PubMed ID: 11359477].

  • 26.

    Cibirka RM, Razzoog ME, Lang BR, Stohler CS. Determining the force absorption quotient for restorative materials used in implant occlusal surfaces. J Prosthet Dent. 1992;67(3):361-4. [PubMed ID: 1507102].

  • 27.

    Ghanbarzadeh J, Sabooni MR, Keshavarz M. Finite Element Stress Analysis on the Effects of the Changes in Length of Pontic on the Stresses Carried from Pontic to Abutments. J Mashhad Dent School. 2007;31(3):231-8.

  • 28.

    Misch CE. Treatment plans related to key implantpositions and implant number. In: Misch C, editor. Contemporary implant dentistry. St Louis: Mosby; 2008. p. 147-59.