A System Dynamics Model to Analyze Nitrate and Ammonia in Reservoirs and Lakes

1. Background

Models, as a simplified picture of reality, are used as scientific tools to solve problems in different fields. Clearly, models never cover all aspects of a real system, but it is important for a good model to cover at least the essential and critical parts of a complex system (1).

Inorganic nitrogen exists in oxidative states such as nitrite, nitrate, ammonium ion and molecular nitrogen (2). These materials convert to each other as a part of nitrogen cycle. Non-biological processes include phase deformations such as evaporation, absorption and sedimentation. The biological deformations include:

1) Inorganic nitrogen absorption by phytoplankton. Although Phytoplankton use both ammonia and nitrate, but they prefer to use ammonia.

2) The process in which organic nitrogen is converted into ammonia is called ammonification which is a complicated process including multiple mechanisms such as bacterial degradation, zooplankton fecal and direct digestion after cell death.

3) Ammonia oxidation to nitrite and then nitrite to nitrate via a selective action of a group of aerobic bacteria. This process uses oxygen and is normally considered as a grade one reaction. As nitrite rapidly converts to nitrate, they are considered in one group in many of the nutrition-food chain models.

4) In anaerobic conditions such as sedimentations, nitrate could act as an electron acceptor for some bacteria. Nitrite is a mediator product and finally free nitrogen is produced (3).

5) Application of nitrogen gas as a nitrogen source is called nitrogen fixation. Only prokaryotes can fix nitrogen gas and among them, photosynthesizing microorganisms and some few other species have the ability to use nitrogen gas (4).

These models were divided into two categories of static and dynamic models (5). Static models show balanced condition, while dynamic models show system changes over the time (6). One of the approaches which are used for dynamic simulation of a complex system is system dynamics approach. System dynamics was founded by Jay Forrester in Massachusetts institute of technology (5). System dynamics is a computer-aided approach to analyze and solve complex problems with a focus on policy analysis and design. System dynamics is applied to a wide range of problem domains. It includes working in euthrophication modeling (7, 8), behavioral analysis (9), urban coastal systems (10), water resources management (11), energy (12), water supply networks (13), nitrogenous compounds (14) and mosquito-borne diseases (15).

Models with a wide spectrum of complexity were applied for water quality management. Ecological modeling of artificial lakes is an example for such a complex and dynamic water quality model. These water bodies interact with human activities (16). Bryhn and Blencker demonstrated that nitrogen fixation is unlikely to be limited by the nitrogen concentration in the lake Erken water (17).

In a research by Zazouli et al. on nitrate removal modeling by Nano-scaled zero-valent Iron, the results indicated a direct relationship between nitrate removal efficiency and the time and amount of Nano-scaled zero-valent Iron (NZVI). Therefore by increasing the contact time and level of NZVI, nitrate removal rate increases as well. In other words, by increase of ionic strength and initial concentration, nitrate removal is reduced (18).

In the work of Williams et al. on ammonium nitrate modeling, it was concluded that the concentration of ammonium nitrate decreased during the period (19).

Schelske et al. studied biological algal response to phosphor and nitrogen enrichment in the Michigan Lake in 1974. They realized that phosphor was the main responsible nutrition of algal biomass increase and algal production, while nitrogen had lower impact (20). Fairchild and Lowe also did similar experiments in 1985 to determine limiting nutrition in the Douglas Michigan Lake; they found that both phosphor and nitrogen could limit total growth (21).

2. Objectives

The current study aimed to introduce a suitable system dynamics model to analyze nitrate and ammonia in reservoirs. The study used Vensim^TM, system dynamics software.

3. Materials and Methods

In this study, ammonia and nitrate were modeled by system dynamics approach. The model structure, along with the data was transferred into Vensim^TM computer software package. This software package is an expert system that facilitates the development of system dynamics models. The proposed model is a zero-dimensional model in which the reservoir is divided into two layers, epilimnion and hypolimnion. Each reservoir layer was considered as a complete mix reactor. Therefore, four state variables were made including ammonia and nitrate concentration in epilimnion and hypolimnion.

After determining the relationship among each of the state variables, all effective parameters and variables were recognized and their graphic schemes were drawn on Vensim^TM page. Then, direction of these relationships was identified. On the other hand, system variables were defined in terms of four main components and each one was created on Vensim^TM design page based on its type. Four components were used in system dynamics to make the model and show cause and effect relations that are 1-stocks or state variables 2-flows 3-arrows or connections and 4-converters or parameters (22). State variable defines ecosystem situation and implies a concept that something could be stoered in it. Flow is a current operation that determines system reservoir contents during a time period. An arrow shows a connection that connects two components in a model. Converter is a variable that determines tone or function rate in a process. A converter can play different roles in a system. The most important role of a converter is determination of rate in a process. Content change speed of any storage is based on this rate (23). Converter can be a constant for an especial ecosystem or a part of an ecosystem (1).

Feed-forward and feedback processes hypotheses are used in a system dynamics approach. A feedback system is influenced by its previous behavior. Those loops are created in this process. The current study also aimed to understand how and why issues are dynamic and also search for management policies to improve the situation (5).

In the next stage, mathematical relationships related to each variable were identified. For this purpose, first, mass balance was written for each state variable. In general, amount of each chemical material in a reservoir could be written as Equation 1:

(1)

Input shows desired pollutant amount [ammonia or nitrate] in a river inflow. The Long Lake reservoir had two inflows, including Nine Mile Dam outflow and little Spokan River. Output shows pollutant amount in outflow of reservoir. Equation 2 was used for the reaction part of Equation 1 (24):

(2)

Ammonium ion is obtained through hydrolysis of dissolved organic carbon and from food-chain respiration. Ammonium ion is reduced through plant intake and nitrification.

Where Fam is fraction of inorganic nitrogen taken from the ammonium pool by plant uptake (24) (Equation 3):

(3)

Nitrate is obtained through nitrification and it is consumed by plants. Equation 4 is used to model nitrate part of the cycle (24):

(4)

In these relationships, V, volume; t, time; a, density of algae; anc, carbon to nitrogen ratio; ana, chlorophyll-a to nitrogen ratio; kg, algal growth rate; Kn, half- saturation constant of nitrogen; ni, nitrate; na, ammonia; nt, total inorganic nitrogen [na+ ni]; T, temperature; Cd, dissolved inorganic carbon; Kra, losses resulted from respiration and excretion in algae; I, light; Ps, phosphorous; Zc, carnivorous zooplankton and Kam, a half-saturation constant for ammonia preference.

The amount of nitrogen released from sedimentations that could result from both re-suspension of sedimentation and re-dissolving of sedimentation nitrogen are considered in a parameter named Sn. The amounts of Sn are proposed in different scientific contexts which the current study used the same amounts.

The rates of most reactions in natural waters increase with temperature. Temperature effect on different rates is identified with Arrhenius equation (24, 25). In the next step, some data such as inflow and outflow are transferred into the model as a table and the related time series was made. In these tables, for example, the relationship between time and river flow entered the model and finally a diagram was constructed. It means that flow is given to the model as a time variable instead of considering it as a constant. It was done for some other variables.

On the other hand, in the current study, the reservoir was divided into two layers [epilimnion and hypolimnion] and each part was considered as a complete mix reactor. These layers are interacting material through distribution coefficient. This coefficient depended on reservoir stratification defined as a function of time in the model.

The model was tested with the data originating from Karkheh Reservoir in Iran. Evaporation based reduction in water of Karkheh reservoir is shown Table 1.

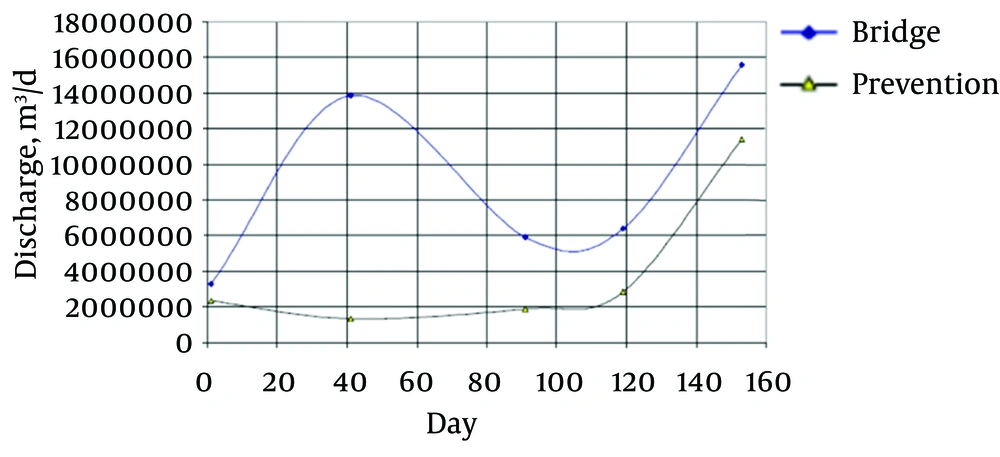
Current discharge in prevent stations and under bridge are shown Figure 1.

Input and Output Discharge of Karkheh

Figure 1.

Input and Output Discharge of Karkheh

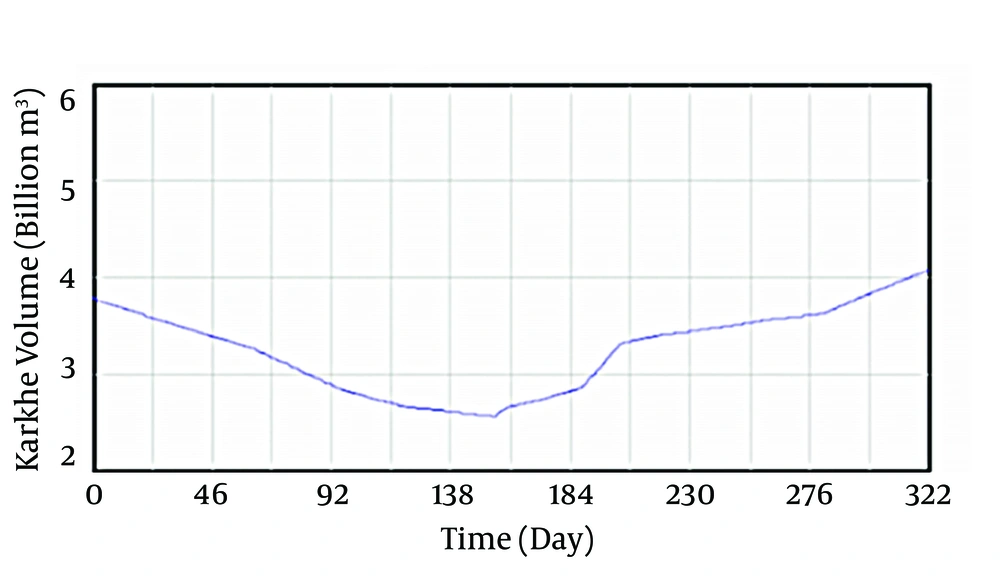
Variation of reservoir volume according to water level and also the relationship between volume and level are calculated. The volume variation in Karkheh reservoir is calculated by model as shown in Figure 2.

Variation of Karkheh Reservoir Volume

Figure 2.

Variation of Karkheh Reservoir Volume

Three important steps in modeling process include verification, calibration and validation (1). Exact date were needed to show the efficiency of this model and its verification. Therefore, the data of Long Lake reservoir in the United States (26) were used. After writing the equations, quality and quantity data of reservoir in 1991 (from June to November 1991) were transferred into the model and usual amounts of parameters (extracted from valid scientific articles) were loaded on to the model. At the next stage, the model was calibrated for long lake reservoir and sensitivity analysis was done for the parameters. If the obtained results were not satisfactory, kinetic parameters in the model were changed. At the final stage, the model was validated using data of 2,000 (from January to December 2000). Data present in the Long Lake reservoir were from 5 stations. Since the reservoir was considered a complete mix reactor in this study, the surface quality data on epilimnion layer depth were averaged and used in the model as that parameter amount on over-layer. This was also done for hypolimnion layer. Distinguishing the boundaries between the mentioned layers was also conducted based on temperature profile in the reservoir depth. The initial conditions correspond to the values obtained at the end of the simulation period.

Model inputs included ammonia and nitrate concentrations. Since simulation was done for both layers of the epilimnion and hypolimnion, input amounts and also temperature were considered for each layer. Epilimnion and hypolimnion temperatures were transferred into Vensim^TM as monthly amounts diagram. Reservoir dimensions, thermocline area, epilimnion and hypolimnion volume, outflow and inflow of reservoir and concentrations of state variables were transferred into the model.

4. Results

Many environmental systems have similar characteristics by which system behavior could be monitored and predicted. A model system could be designed based on these items. The major benefit of making environmental systems is to determine these characteristics and appropriate exploitation of system components [such as appropriate combination of storage, flow, converter and connector.

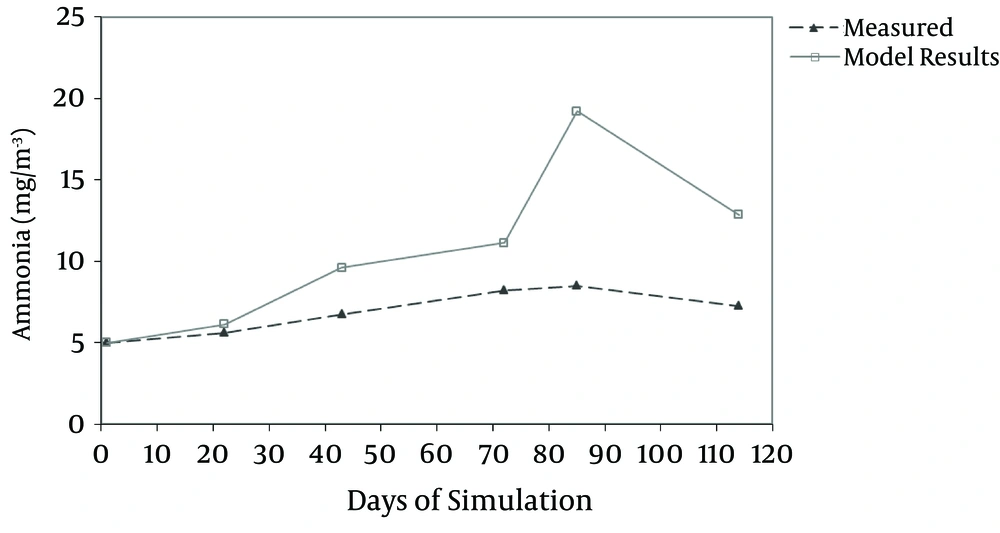
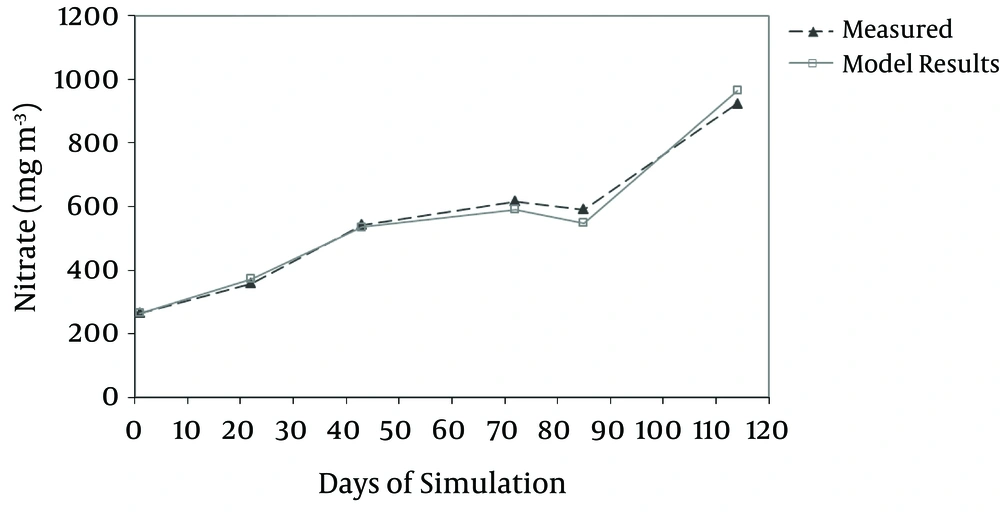
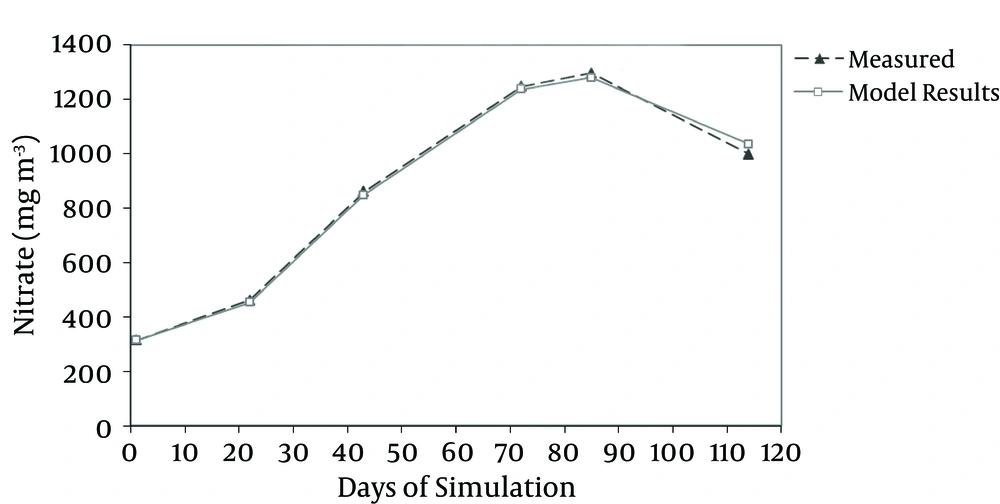
A comparison of the measured and simulated mean values showed that the simulation was in good agreement with the measured data in the epilimnion and hypolimnion layers of the reservoir (Figures 3 and 4, respectively).

Ammonia Modeling Results Comparison in Epilimnion With Measured Data in Long Lake in 1991

Figure 3.

Ammonia Modeling Results Comparison in Epilimnion With Measured Data in Long Lake in 1991

Ammonia Modeling Results Comparison in Hypolimnion With Measured Data in Long Lake in 1991

Figure 4.

Ammonia Modeling Results Comparison in Hypolimnion With Measured Data in Long Lake in 1991

In the model sensitivity analysis, coefficients related to light were changed and it became clear that light was a very effective parameter and it was considered as the most important parameter of the model.

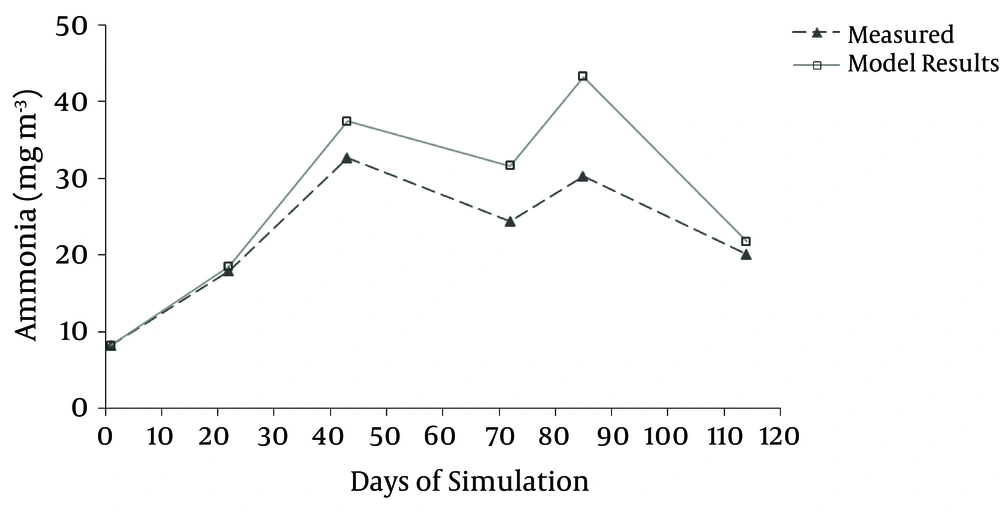
In Figures 5 and 6, nitrate modeling results are compared in the epilimnion and hypolimnion with measured amounts.

Nitrate validation results comparison in the epilimnion with those of the measured data in Long Lake in 2000

Figure 5.

Nitrate validation results comparison in the epilimnion with those of the measured data in Long Lake in 2000

Nitrate Validation Results Comparison in Hypolimnion With Measured Data in Long Lake in 2000

Figure 6.

Nitrate Validation Results Comparison in Hypolimnion With Measured Data in Long Lake in 2000

5. Discussion

Today, powerful models should have special characteristics in terms of environmental issues in order to play an important role in solving problems among major groups and organizations effective on ambient quality. A good model should have capability, adjustment and availability (25). Capability includes model applicability, using new data and its competitive power. Model availability also includes three capabilities of networking, user-friendly and low cost. Vensim^TM was employed to develop a model to manage ammonia and nitrate in the long lake reservoir.

Ehrampoush et al. addressed nitrogen and phosphor modeling in wastewater stabilization ponds of Yazd. In his MSc thesis, the impact of climate factors such as temperature, evaporation and precipitation on nitrogen dynamicity and algal concentrations were investigated. In comparison with the current study, since the depth of stabilization oonds was lower than that of the lakes, Ehrampoush et al. assumed the entire pond as a mixing reactor and did not work with two layers (27).

In another study conducted by Vezjak et al. in Turkey, dynamicity of nutrition and also phytoplankton were assessed in the Glamsou Lake. In the mentioned model, the effects of different parameters on phytoplankton’s growth were evaluated; in which temperature was considered as an important factor in kinetic coefficient, in such a way that the impact of temperature on other variations was linear. In other words, the dynamicity of variables such as nitrate, phosphate and the like, are the linear function of temperature. In the current study, the same trend was observed (28).

Samaei et al. modeled eutrophication in the Long Lake reservoirs in the USA. In this model, nitrogen was not introduced as a limiting factor on algal growth. In this study, nitrogen was not a limiting factor either (29).

All the related rates were influenced by temperature, and the temperature of water was considered in all the rates (temperature correction coefficient was used). Humidity and evaporation, level of dam input and output were also considered.

Lack of complete accordance between the model results and measurement observation could be attributed to the processes and events considered in the model; for example, nitrogen fixation, change and conversion of organic nitrogen to ammonia and nitrate.

The results indicated that the output of the model for the beneath layer had better accordance with the measured values, in comparison with that of the outer layer. This could be due to higher modification in the outer layer. In other words, the water quality in the beneath layer was almost constant and followed more obvious patterns; while, more interfering factors existed in the outer layer.

In general, the following conclusions were drawn:

- A zero-dimensional System dynamics model for simulation of nitrate and ammonia was proposed and applied to the long lake reservoir in the United States. This model made total assessment of reservoir quality, therefore the speed to get the results and flexibility of the model was the unique feature of this model. If necessary, using this model for other reservoirs or adding more complexities to the model is easily applicable. Also, if some of these amounts were not available, they could be removed from the model. It seems that due to the requirements in different contexts regarding environmental health and bio-echology, using and applying dynamic models should be seriously considered by experts.

- The dynamic modelling results evaluated with the results from the Long Lake reservoir measurement campaigns are good.

According to the obtained results and their comparison with the nitrate and ammonia levels measured in the reservoir, it can be said that this model was a simple and at the same time accurate model to model nitrate and ammonia in the reservoirs. Nutrition-oriented model of system dynamicity needs less data in comparison with the other models. Thus, it is a cost-effective model with acceptable results.

Regarding all the above mentioned and the obtained results, the following suggestions could be presented:

1- The system dynamicity model can be divided into smaller parts. It means that for each station a complete model could be applied. In this case, these sub-models can be linked together via water speed in reservoir and longitude diffusion coefficient consideration.

2- The vertical layers can be three or more. In this case, nutrition deposition would be added for the corresponding added layers.

3- Climate and light data should be added to the model as the function of time.

4- The amount of nitrogen added via precipitation should be measured and transferred into the model.

5- Phytoplankton has different shapes with specific growth coefficients; therefore at least two or three phytoplankton species should be modeled.