1. Background
Recognized as a three-dimensional spinal deformity, scoliosis refers to the deviation of the spine greater than 10 degrees, the lateral curvature, and vertebral axial spine rotation (1). According to studies, scoliosis affects 2 - 5% of the world’s population, 65% of whom are idiopathic (2). According to the evidence, there are many variations between idiopathic scoliosis in males and females. However, while males and females are similarly affected by mild idiopathic scoliosis, extreme deformity in girls is more prevalent (3, 4). Early detection of scoliosis is essential to prevent the progression of deformity (5). In addition, measuring the degree of deformity is crucial to screen the progress of scoliosis, operative planning, and correction of the spine (6).
Despite significant progress in cross-sectional imaging over the past decades, the most important imaging of scoliosis is still classical radiography (7). Cobb technique is used to evaluate radiographs to assess the spinal curvature in scoliosis (8). Moreover, the Cobb angle is measured for the primary thoracolumbar curve. The angle of Cobb is measured by calculating the average angle from the upper end of the vertebra to the lower end (9). Generally, lines are drawn manually onto the spine’s hard copy computer, and angles are determined using a protractor (10). However, the manual measurement has several errors, including time-consuming (about 20 minutes for each case) in the clinical environment, which requires a high precision (10).
With the development of computer technology, the use of computers to measure the Cobb angle has gained growing popularity in clinical practices. There is so-called digital computer-assisted (semi-automatic) in addition to the manual procedure (9, 11, 12) and automatic (13, 14) frameworks. Various reviews have demonstrated an improvement in the measurement accuracy of this method compared to the manual measurement technique (15, 16). In computer-aided method developed by Zhang et al. (13), the Cobb angle and vertebral rotation were semi-automatically measured using the Hough transform and snake model. Measurements resulted in average intra- and inter-observer errors less than two and three degrees, respectively. In the research by Pan et al. (17), Mask regions with convolutional neural networks (R-CNN) model was used to Cobb angle measurement in chest X-rays from lung cancer screening. Their method first needs to find midpoints of the superior and inferior endplates of each vertebral body. In another research by Toan et al. (12), Cobb angle measurement was done by a semi-automatic method based on a deformable model with fuzzy spatial relations. Likewise, in 2008, Allen et al. proposed a robust Cobb angle test for idiopathic scoliosis using effective form models (14).
In the above studies, to train the code to identify the vertebrae, the researchers need a training collection of radiographs reflecting curves seen in scoliosis. Also, active shape models can not deviate significantly from variations, and can therefore only produce similar shapes to the training set. In addition, the object’s boundary is defined by manually N landmarks around the object’s perimeter in a photo. This is time-consuming and increases the likelihood of human error.
2. Objectives
In this study, authors developed a computer-aided measurement system (CAMS) to provide a repeatable and reproducible approach to help assess scoliosis by measuring the Cobb angle. The developed CAMS aimed to reduce manual intervention, as well as measurement error and time. This procedure assists in the suitable and easy assessment of scoliosis, thus having a positive effect on the treatment process of patients.
3. Methods
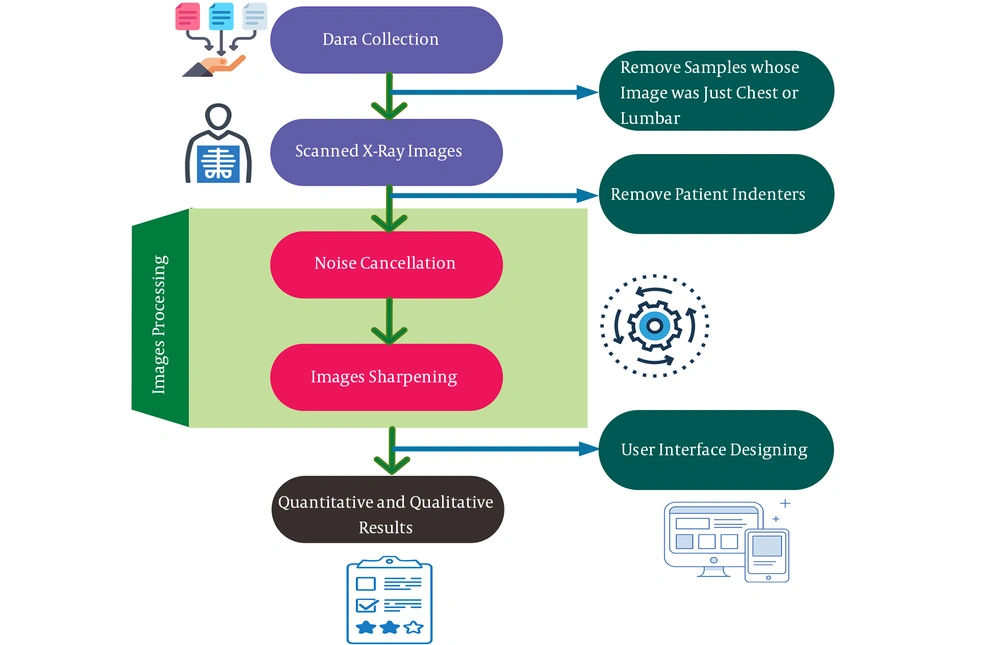
In this research, the system was developed in several steps, as summarized in Figure 1.
3.1. Data Collection
Anterior-posterior (AP) radiographs of patients diagnosed with scoliosis referred to Pezhvak radiography clinic in Tabriz, Iran, were examined during February - April 2017. After applying the inclusion and exclusion criteria, 98 images were included in the study.
The images were anonymous and included single curve (C), double curve (S), or both shapes. The subjects included 63 females and 35 males aged above 12 years (18 ± 2 years). Patients ranging from curvatures with small (> 15°) to wide (< 68°) Cobb angles were included in the study. The primary inclusion criteria were diagnosis of idiopathic scoliosis and Cobb angle below 90 degrees. The patients were excluded if they had previous brace or spine surgery and other musculoskeletal or neurological disorders.
3.2. Preprocessing
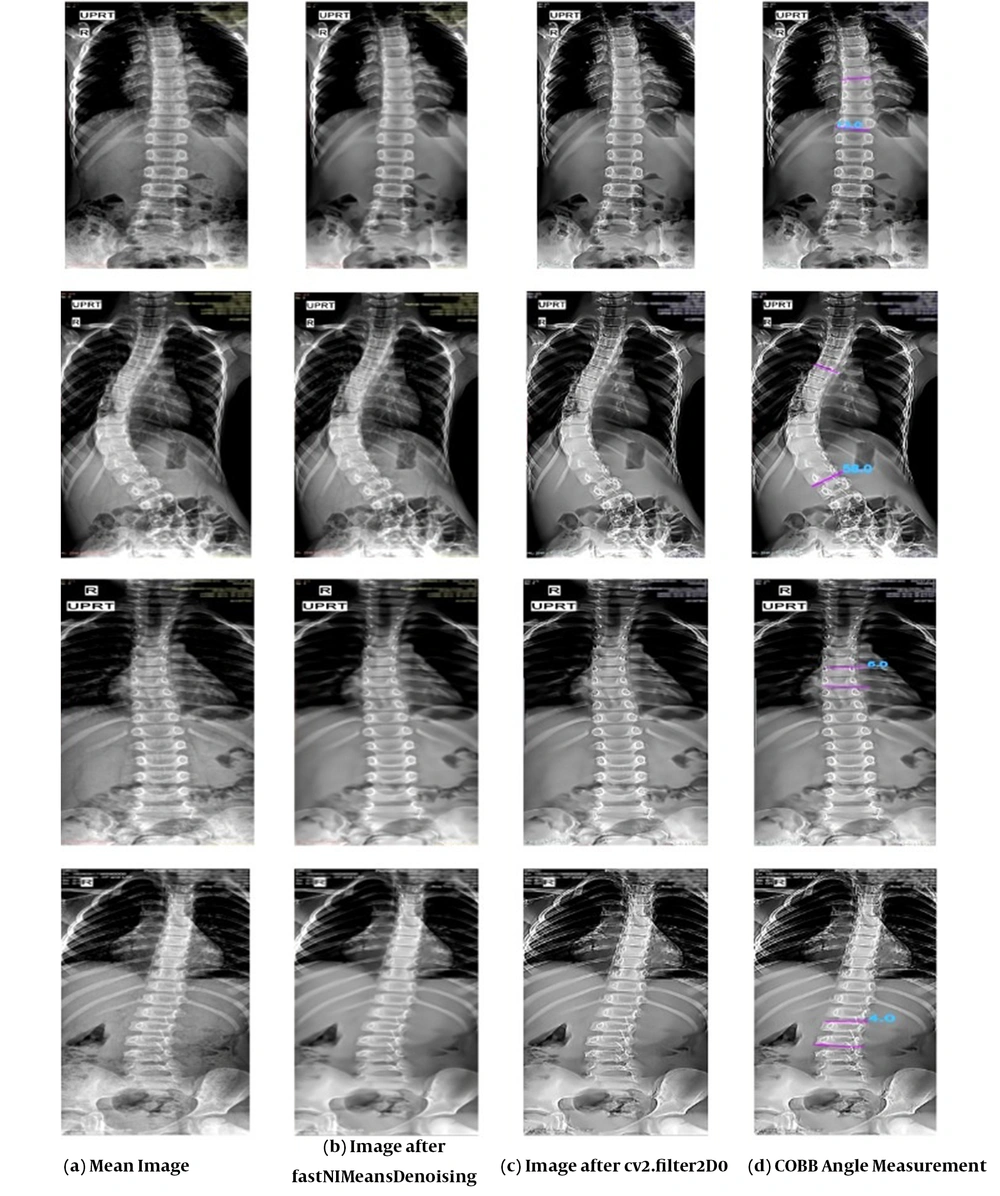
Presence of any type of noise significantly complicates the extraction of the correct information or leads to different results of subsequent stages. In this stage, the main procedure for image enhancement is noise removal. The algorithm of non-local (NL) means, first introduced by Buades et al. (18) is based on the natural redundancy of information in images to eliminate noise. This filter allows the avoidance of the commonly used neighborhood filters well-known artifacts. We used the openCV routine fastNlMeansDenoising. The aim of this algorithm is to reduce the computational costs by a fast calculation of similarity index. In this algorithm, the approximate measurement of the similarity of neighborhood windows, as well as the use of efficient summed square image scheme and Fast Fourier transform, are introduced. This algorithm provides 50 times better results than the original NL-means algorithm. In this research, the fast non-local filter parameters cv2.fastNlMeansDenoising (output 1, 15, 17, 21) were measured. Image processing steps are shown in Figure 2, and Figure 2B presents the image after noise cancellation.
3.3. Spine Extraction and Analysis
The next step for spine extraction is feature extraction. Edge detection is a fundamental and basic set of mathematical methods among all the different types of tools available for extraction or detection of features. The aim of edge detection is to recognize regions in a digital image where image brightness is sharply changed. Sharpening is a tool that derives its name from the fact that edges are enhanced by a procedure that subtracts from the original image an unsharp or smooth version of an image. Compared to normal images, it is easier to detect features from a smooth and crisp image. The image is distorted by the low-pass filter kernel coiling of the image. In this research, the cv2.filter2D (img, -1, kernel_sharpen_1) parameters in OpenCV were applied, and the result is shown in Figure 2C.
3.4. Detecting the Vertebrae Lines and Cobb Measurement
Because of noisy radiographs, isolated horizontal vertebral endplates are discontinuous in nature. The upper and lower end of vertebrae are distinguished by the inclination of the vertebrae’s horizontal endplates. By CAMS, first, each angle is calculated in relation to the X axis, and then they are combined together. The result of the Cobb angle measurement is shown in Figure 2D.
3.5. System Design
All steps of the study were coded in Python 2.7 by importing scientific libraries such as OpenCV, Numpy, Matplotlib, and mathematical functions to facilitate the computations.
3.6. Manual and Digital Measurements
Five independent observers performed two sets of analyses (two orthopedic surgeons, two physiotherapists, and one radiologist). In the first set, the traditional manual method was used to evaluate 98 X-ray images. The observers were told to use their instruments (i.e., pencil and protractor) for each measurement to complete the task. All 98 X-ray films were analyzed three times at a minimum interval of two weeks between the repeated measurements. The final number of evaluations performed by each of the five observers was reported to be 1470 manual assessments. The observers did not have any information about other individuals’ measurements and their own previous data from the same film. The observers were trained to use the software developed for the analysis before starting the second set (i.e., the electronic evaluations).
3.7. Statistical Analysis
In this research, the repeatability and reproducibility of Cobb measurements of the manual and digital methods were applied to assess and compare intra- and inter-observer differences. Statistical analysis was performed in IBM SPSS Statistics, version 16. Both intra- and inter-observer reliability were achieved using the single intraclass correlation coefficient (ICC) [95% confidence intervals (CI)] value of the single measure (2-way random effects model, absolute agreement). So, ICC values less than 0.5, between 0.5 and 0.75, between 0.75 and 0.9, and greater than 0.9 indicated a poor, moderate, good, and excellent reliability, respectively. Regarding the knowledge about the data variability, the mean absolute difference (MAD) was used, and to measure the scatter of test scores measured around a “true” score, the standard error measurement (SEM) was calculated for all corresponding intra- and inter-observer reliability estimates. Measures from all observers were compared simultaneously for each parameter, as well as separately between each pair of observers. In addition, to recognize the intolerance and limits of agreements between repeated measurements by each observer and by various observers, the Bland-Altman plot was used. The student t-test was exploited to assess the differences between the manual and digital time measurements.
4. Results
4.1. CAMS
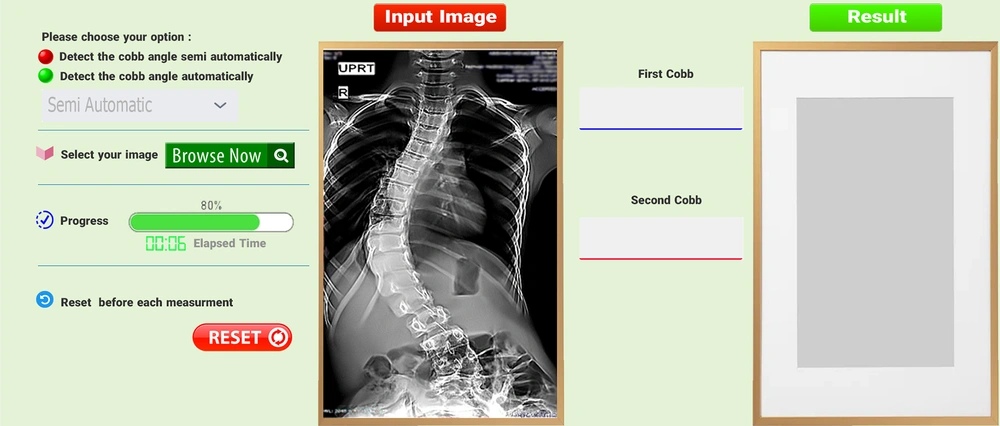
The CAMS user interface is shown in Figure 3.
In our system, when the image was imported, a quick preprocessing was performed before the measurement process. The user selected the superior endplates of the upper candidates vertebral and then selected inferior endplates of the lower candidate vertebral. It was the only intervention carried out by the observers, and the remaining steps were performed automatically. After selection, the Cobb angle was calculated automatically.
4.2. Repeatability of the Manual and CAMS Cobb Angle Determination
The statistical results for the intra-observer analysis are shown in Table 1, according to which ICCs ranged from 0.94 - 0.99, and the MAD between manual and CAMS was less than 3º. In addition, the great MAD between the repeated data sets amongst all five observers in the manual method was 2.13º, whereas the mean (MAD standard deviation) of observers was 2.01º. In terms of Cobb angle determined with CAMS, the largest MAD was 2.04º, and mean MAD was 1.71º. The combined SEM between all five observers for intra-observer measurements manually and by CAMS were 1.79º and 1.27º, respectively.
| Variables | Observer 1 | Observer 2 | Observer 3 | Observer 4 | Observer 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Manual | CAMS | Manual | CAMS | Manual | CAMS | Manual | CAMS | Manual | CAMS | |
| MAD ± SD (°) | 2.12 ± 1.1 | 1.97 ± 0.9 | 1.98 ± 0.7 | 1.53 ± 0.7 | 2.13 ± 1.1 | 2.04 ± 1.2 | 1.87 ± 0.9 | 1.61 ± 1.0 | 1.95 ± 0.9 | 1.43 ± 0.8 |
| SEM | 1.13 | 1.22 | 1.83 | 1.18 | 1.45 | 1.34 | 1.89 | 1.22 | 1.78 | 1.59 |
| ICC | 0.97 | 0.98 | 0.95 | 0.98 | 0.97 | 0.98 | 0.94 | 0.96 | 0.97 | 0.99 |
| CI | 0.94, 0.98 | 0.95, 0.99 | 0.93, 0.97 | 0.96, 0.99 | 0.95, 0.98 | 0.96, 0.99 | 0.92, 0.95 | 0.94, 0.98 | 0.94, 0.99 | 0.97, 0.99 |
Statistical Results for the Intraobserver Analysis
4.3. Reproducibility of the CAMS Cobb Angle Determination
Table 2 shows the analysis of the inter-observer and describes the main statistical differences between the methods of manual and CAMS. According to the results, the inter-observer reliability in CAMS was excellent as the ICC value of 0.97 with 95% CI. In addition, the CAMS mean absolute difference was 2.18 ± 2.01 degrees.
| Statistical Parameters | Manual | CAMS |
|---|---|---|
| MAD ± SD | 2.96 ± 2.13 | 2.18 ± 2.01 |
| SEM | 2.28 | 2.23 |
| ICC | 0.95 | 0.97 |
Inter-observer Analyses
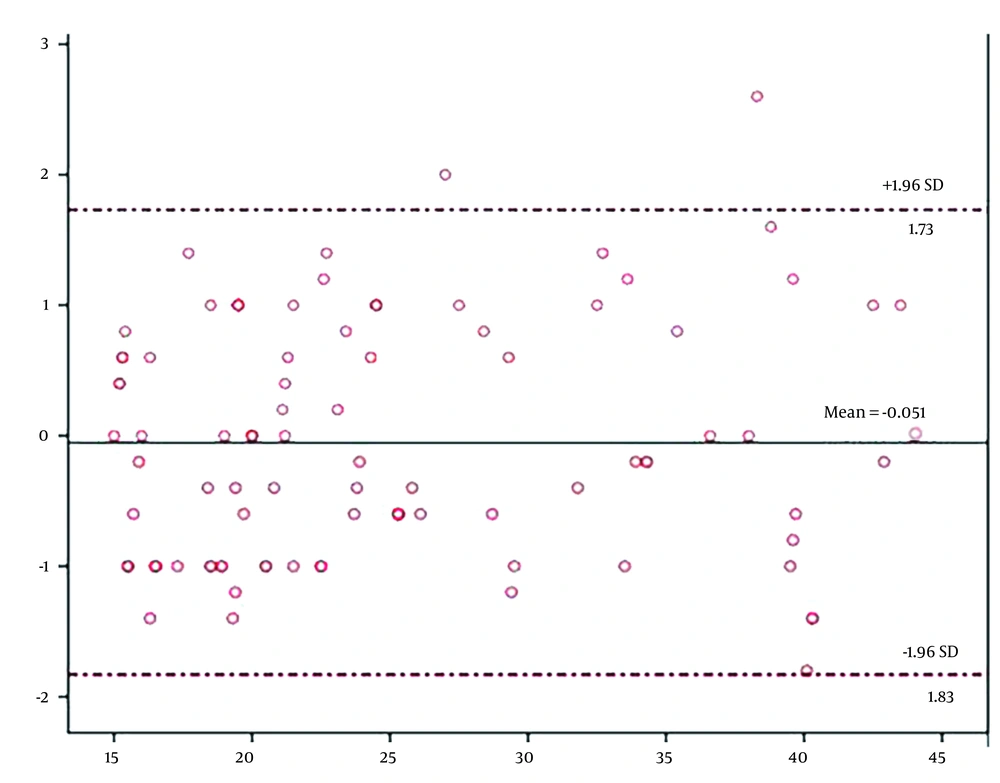
The Bland-Altman plot (Figure 4) showed a good agreement between the results obtained by the two methods with all data points located inside ± 1.96 SD from the mean, with a mean difference of -0.051° and 95% CI (between -1.83° and 1.73°).
As shown in Table 3, the mean duration of manual measurement was four minutes and 35 seconds, which was reduced to one minute and 20 seconds when the CAMS was applied. Based on t-test results, the reduction in time was significant.
| Variables | Number | Mean ± SD (Second) | t | P-Value |
|---|---|---|---|---|
| Manual | 98 | 297.37 ± 32.34 | 49.61 | < 0.001 |
| CAMS | 98 | 84.5 ± 10.21 |
Duration of Measurements
5. Discussion
Since curve progression in consecutive radiographs is characterized as a Cobb angle shift of > 5° and different severity rates that lead to alternative treatment options, it is important to verify the accuracy of these parameters to provide patients with the best treatment management (19). Some studies indicated that the accuracy of calculations for evaluating the Cobb angle improved by digital methods (15, 16). However, few studies did not identify any significant differences between manual and electronic approaches (20). Generally, finding optimal methods for improving the accuracy and speed of computerized Cobb angle measurement is the main goal of new studies in this field. Supported by our statistical analysis, the designed measurement system was able to produce a reliable calculation with minimal bias. In the present study, the MAD in CAMS was less than 2°, which was below the 5° threshold of changes that could affect the treatment decisions. In a study by Zhang et al., the lowest error rate was reported less than 3° (13). Due to the use of two methods simultaneously and more user intervention, the error in the study by Zhang et al. was higher than our study.
The mean of MAD obtained by the CAMS measurement was lower than the calculated value in previous studies (7, 17, 21). These values indicate a high probability of belonging to the same population for the manual and digital measurements performed by each observer. However, due to the lower number of samples and observers, the obtained value was higher than in other studies (13, 19). Compared to previous research (17, 19), where values for the intra-observer ICCs (0.91 - 0.99) and inter-observer ICCs (0.93 - 0.99) of the Cobb angle were obtained, our findings showed similar results (intra-observer: 0.96 - 0.99; inter-observer: 0.97), which explained a strong correlation between the measurements.
Compared to Allen’s method for Cobb angle measurement (14), the proposed system required no training process. Therefore, the results were independent of the collected data. Compared to the Chockalingam’s method (22), where at least 16 points must be assigned manually, this system required fewer user interventions. The time taken in the manual measurement was calculated in the range of 10 - 15 minutes in the major section of studies (11, 12, 23-25), depending on the familiarity level of observers to the Cobb angle measurement method. In the current study, the mean time of the Cobb angle measurement was reported as approximately four minutes based on the familiarity of the observers with the method. On the other hand, the meantime of computerized measurement was reduced to one minute and 20 seconds from image loading to displaying the results. Compared to other studies, our findings showed a shorter duration, with the exception of the study by Chan et al. (19), where the duration of the process was reported to be 14 seconds considering that the time was related to algorithm performance and not the whole process. The method used in the study by Pan et al. (17) is based on finding the vertebrae midpoint. Since lateral deviation and axial rotation of the vertebrae occur at scoliosis, finding the middle point may not be accurate. In our study, vertebrae rotation did not affect the accuracy of the method.
In the current research, the designed system had a high performance and usability. It calculated the measurements with minimal user involvement and optimal speed and performance. A strength point of the current system was its Python- and OpenCV-based foundation with very low dependency on the platform. This feature simplifies the installation of the system in various environments in an operational manner, such as Linux, Windows, and Android OS. Most previous studies depended on MATLAB software and did not target the point of care and clinical usage, and research goals.
One of the major drawbacks of the present study was that all observers in our study were familiar with the Cobb angle measurement method because observers with lack of familiarity with Cobb angle measurement will help to report the accuracy of the system with a higher confidence. The quality of images was another limitation of this study. Since the quality of images depended on imaging device, so images taken with advanced devices affected the results.
The main strength of the present study was the high statistical power of the study since the 98 X-ray images used in the study led to over 980 intra-observer comparisons for each observer, as well as approximately 980 inter-observer comparisons. Both participants were blinded to the information provided by the subject, and the Cobb did not receive pre-selected end vertebrae, which created a similar medical environment scenario. The radiographs of idiopathic scoliosis patients were taken from the local hospital registry, which were indicative of curves in a specialist scoliosis clinic treated conservatively. Nearly all reliability coefficients represented good-excellent reliability, which supported the use of CAMS for clinical implications. According to the results of the current research, the Cobb angle measurement method had the potential to reduce human error and improve the reliability of radiographic measurements in clinical situations.
5.1. Conclusions
According to our results, the user has selected only inferior endplates of the lower candidate vertebral on each radiograph. The system automatically calculated the Cobb angle and assisted in making decisions. Experiments demonstrated its appropriate repeatability and reproducibility. The CAMS is an effective and reliable approach for assessing scoliotic curvature in the standing radiographs of thoraco-lumbar. Also, CAMS can accelerate clinical visits, and its calculation results are reliable.