1. Background
Chronic kidney disease (CKD) is a worldwide health problem with increasing incidence, prevalence, and burden at an alarming rate (1, 2). It is also a risk factor for cardiovascular disease. In 2017, about 1.2 million people worldwide died of CKD (3, 4).
End-stage kidney disease (ESKD) is the last stage of CKD in which the glomerular filtration rate is less than 15 mL/min/1.73 m2, and the patient needs long-term dialysis such as hemodialysis (HD), peritoneal dialysis (PD), or kidney transplantation to survive (5).
In addition to debilitating psychological consequences and disrupting the quality of life of patients and their families, ESKD has significantly affected the economic situation of patients and communities through direct and indirect costs (6). Despite the dramatic success of replacement therapies in recent decades, the mortality rate in ESKD patients remains high compared to the general population (7). The prevalence of ESKD is increasing, possibly due to improved patient survival, demographic changes, increased risk factors for ESKD such as diabetes mellitus, and expanded access to kidney replacement therapy (KRT) (8, 9). The incidence of HD patients with ESKD is increasing worldwide (10). Furthermore, the average age of onset of HD patients is increasing globally, which is one of the most critical factors in the survival rate of HD patients (9, 11, 12). It is necessary to determine the survival rate of HD patients and the factors affecting their survival duration. Also, HD patients comprise a vulnerable population with a cumulative three-year survival rate of approximately 50% (13).
2. Objectives
Survival analysis is an essential tool for appraising the time interval of the event of interest in order to plan or promote appropriate interventions and care services. In this study, we address the factors related to the survival rate of HD patients and introduce the application of a competing risk approach for survival analysis.
3. Methods
This study was performed to analyze the survival rate of ESKD patients over 20 years of age who were registered in the HD wards of teaching hospitals in Khorramabad, Iran, and started HD from January 2011 to December 2016. The end of the study follow-up period was December 2021. Inclusion criteria were at least 90-day history of HD and having CKD. Patients diagnosed with acute kidney disease (AKD) were excluded.
A questionnaire was designed, and data were obtained from hospital records. Some patients’ medical records were incomplete, and they were contacted and interviewed to complete the data. Finally, 214 patients who met the study eligibility criteria were evaluated.
In recent decades, there has been an increasing tendency to consider competing risks in survival analysis studies, but due to the lack of user-friendly statistical software programs, such analyses are less commonly reported in medical journals (14). In studies to determine the survival rate of HD patients, kidney transplantation is considered a competing risk or competing event in which its occurrence either prevents or alters the probability of the event of interest (15). In this study, we considered death (evaluated as all-cause mortality) and kidney transplantation as the event of interest and competing risk, respectively. Other events were considered censored. To estimate the rate of the event of interest, we performed a competing risk analysis and estimated cumulative incidence functions (CIF) to overcome overestimation (16, 17).
We used Gray's test for comparing two or more cumulative incidence functions that is analogous to the log-rank test for the Kaplan-Meier estimator (18). Also, instead of Cox proportional hazard regression, we used Fine and Gray competing risk regression to model the relationship between the event of interest and covariates (demographic and primary underlying diseases). The Fine and Gray model, which provides subdistribution hazard ratios, is the preferred method for more precisely predicting the patient's risk, i.e., the possibility of outcome for the patient at a given time in a prognostic study (19, 20). We must mention that we also performed a Kaplan-Meier estimator survival analysis to compare its results with the CIF estimates. R statistical software version 4.1.2 (package cmprsk) with the application of the function CumIncidence developed by Scrucca et al. (21) was used for subdistribution analysis of competing risks, including the estimation of cumulative incidence curves and Gray’s test.
For obtaining robust standard errors, we used Stata v. 16 (stcrreg command) for Fine and Gray regression analysis using the maximum likelihood estimation. According to the univariate Gray’s test results, we entered covariates in the regression model and finally achieved the most fitted model with the highest Log pseudolikelihood. For all analyses, a significance level of 0.05 was considered. The Ethics Committee of Lorestan University of Medical Sciences approved the proposal with code number IR.LUMS.REC.1399.136.
4. Results
Demographic characteristics of the hemodialysis patients participating in the study are shown in Table 1.
Table 1.Demographic and Basic Characteristics of Hemodialysis Patients
| Variables | No. (%) |
|---|---|
| Sex | |
| Female | 89 (41.6) |
| Male | 125 (58.4) |
| Place of residence | |
| Rural | 54 (25.2) |
| Urban | 160 (74.8) |
| Education | |
| High school diploma or above | 39 (18.2 ) |
| Illiterate or below high school diploma | 175 (81.8 ) |
| Marital status | |
| Single | 30 (14) |
| Married | 184 (86) |
| Dialysis sessions per week | |
| Two | 32 (15) |
| Three or more | 178 (85) |
| Tobacco consumption | |
| No | 154 (72) |
| Yes | 60 (28) |
| Final outcome | |
| Censored | 66 (30.8) |
| Death | 123 (57.5) |
| Kidney transplantation | 25 (11.7) |
There were no significant differences between males and females in age at the initiation of HD, age at death, and age at kidney transplantation.
Mean and standard deviation (SD) for age at the initiation of HD, age at death, and age at kidney transplantation for hemodialysis patients were 58.42 ± 16.04, 67.30 ± 12.76, and 45.72 ± 14.59 years, respectively. They were 25.41 ± 17.67 and 21.44 ± 13.78 months for time intervals from the initiation of dialysis to death and to kidney transplantation, respectively.
Approximately 70 (32%), 24 (11%), and 32 (15%) of HD patients had underlying diseases diabetes, glomerulonephritis, and kidney stones, respectively. Sixty (28%) patients were current and/or previous smokers, and 107 (50.2%) patients had hypertension.
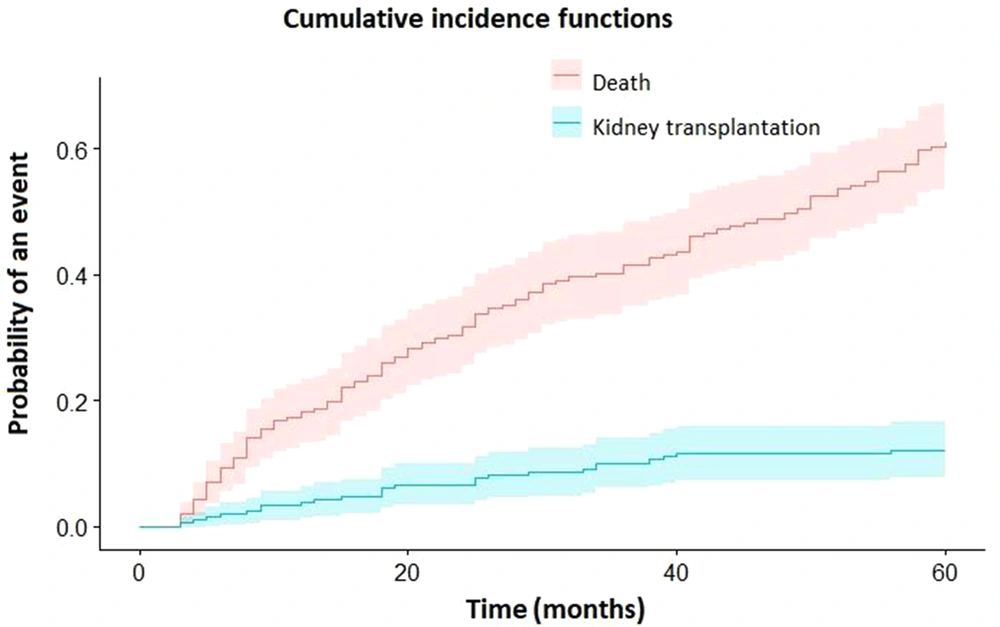
Cumulative incidence estimates of death and kidney transplantation in hemodialysis patients are displayed in Table 2 and Figure 1. For comparison, the estimates of survival and death (1-survival) calculated by the Kaplan-Meier estimator are also presented in Table 2. As can be seen, the results obtained for the mortality of hemodialysis patients by Kaplan-Meier are overestimated for different time intervals.
| Analysis Approach | Kaplan-Meier Estimator | Competing Risk Cumulative Incidence | ||
|---|---|---|---|---|
| Event | Survival | Death (1-Survival) | Death | Kidney Transplantation |
| Time (mo) | ||||
| 12 | 0.814 ± 0.0269 | 0.186 | 0.183 ± 0.026 | 0.038 ± 0.013 |
| 24 | 0.67 ± 0.0332 | 0.33 | 0.317 ± 0.032 | 0.066 ± 0.017 |
| 36 | 0.56 ± 0.0357 | 0.44 | 0.416 ± 0.034 | 0.101 ± 0.021 |
| 48 | 0.462 ± 0.037 | 0.538 | 0.499 ± 0.035 | 0.116 ± 0.022 |
| 60 | 0.328 ± 0.0365 | 0.672 | 0.609 ± 0.035 | 0.12 ± 0.023 |
a Values are expressed as estimate ± SE.
b Estimates of death calculated by the Kaplan-Meier estimator are also shown.
Figure 1.
The cumulative incidence functions of death and kidney transplantation months after initiation of HD (confidence intervals are presented in light colors).
According to the competing risk approach, the risks of death in patients in the first, second, third, fourth, and fifth years were 18.3%, 31.7, 41.6%, 49.9%, and 60.9%, respectively, and the risk of kidney transplantation in patients for the same years were 3.8%, 6.6%, 10.1%, 11.6%, and 12%, respectively.
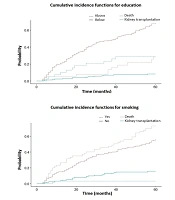
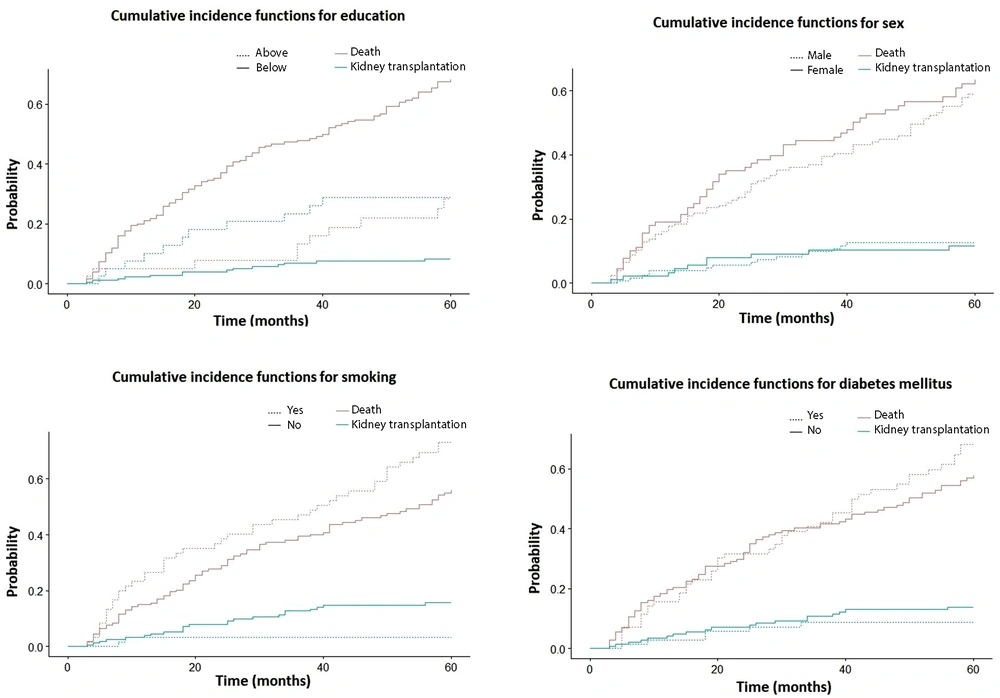
We tested the relationship between various demographic factors such as hospital, education, sex, and residence place, and underlying diseases such as diabetes mellitus, glomerulonephritis, hypertension, and urinary stones and the event of interest (death) separately as univariate analysis using Gray’s test and a statistically significant result was observed for some of them: age at the initiation of HD (P-value = 0.000), education (P-value = 0.000), and smoking (P-value = 0.022). Sex (P-value = 0.354), diabetes mellitus (P-value = 0.343), and other covariates were not associated with mortality (Figure 2).
Figure 2.
Graphs for demonstrating the relationship between different covariates and death (red lines) and kidney transplantation (cyan lines). There is a significant gap between lines of the categories of education for both death and kidney transplantation.
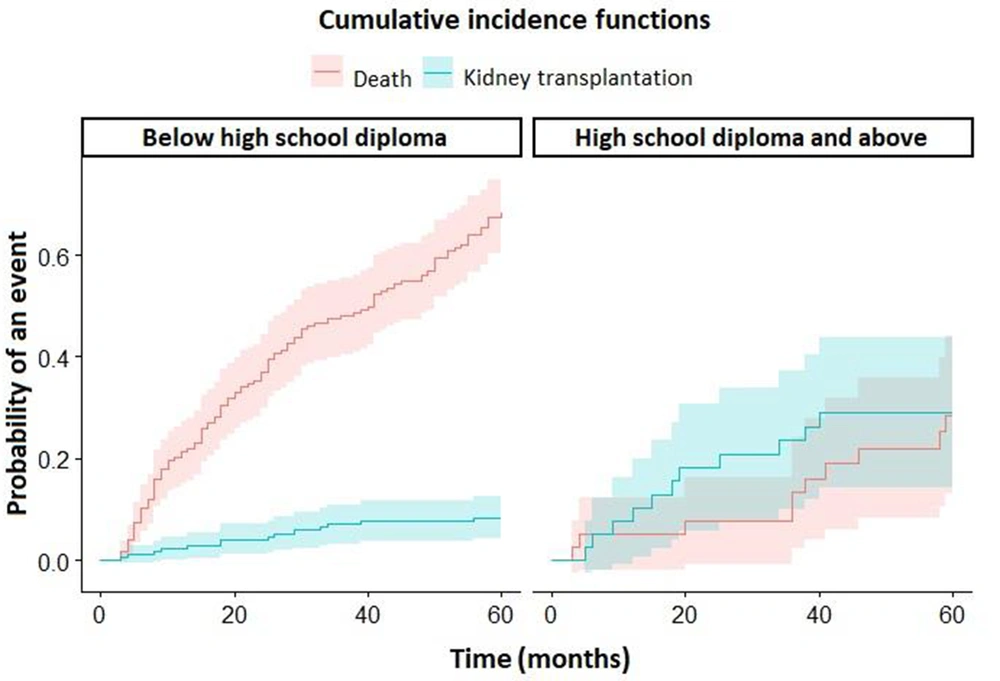
Figure 3 shows the cumulative incidence functions of death and kidney transplantation in two separate panels according to the education level of participants.
Finally, a regression model was developed using the Fine & Gray method to test for the covariates of demographic and primary underlying diseases. The final modeling findings are shown in Table 3.
Figure 3.
The cumulative incidence functions of death and kidney transplantation months after initiation of HD (confidence intervals are presented in light colors)
Table 3.Regression Modeling of the Relationship Between the Death of Hemodialysis Patients and Predictor Variables Based on the Fine and Gray Method
| Covariate | SHR | Robust Std. Err. | z | P-Value | [95% Conf. Interval] | |
|---|---|---|---|---|---|---|
| Education | 0.512 | 0.172 | -1.99 | 0.047 | 0.266 | 0.991 |
| Age at the initiation of HD | 1.043 | 0.008 | 5.67 | 0.000 | 1.028 | 1.059 |
| Diabetes mellitus | 1.346 | 0.250 | 1.60 | 0.109 | 0.935 | 1.937 |
| Glomerulonephritis | 1.601 | 0.475 | 1.59 | 0.113 | 0.895 | 2.863 |
Abbreviation: Std. Err., standard error.
5. Discussion
This study aimed to determine the five-year survival of HD patients using the competing risk analysis approach. The 1, 2, 3, 4, and 5-year cumulative incidence functions for death of HD patients were found to be 18.3%, 31.7%, 41.6%, 49.9%, and 60.9%, respectively. Correspondingly, the survival rate for years 1, 2, 3, 4, and 5 can be assumed to be 81.7%, 68.3%, 58.4%, 50.1%, and 39.1%, respectively. In this study, the results of the Kaplan-Meier estimator are slightly more than those of CIF, as is indicated in the literature as an overestimation (16, 17, 21).
Almost all studies on the survival rate of HD patients have applied Kaplan-Meier estimator as the analysis method. Baladi et al. in 2010 studied 185 HD patients and reported 1, 3, and 5-year survival rates of 89.2%, 69.2%, and 46.8%, respectively, after the initiation of HD (22). Also, in 2016, Ossareh et al. analyzed survival data of 560 HD patients and determined 1-, 3- and 5-year survival rates as 91.9%, 66%, and 46.3%, respectively (23).
Afiatin et al. reported the 5-year survival rate of 3,199 HD patients who had been registered from 2007 to 2018 and had undergone a five-year follow-up period on December 31, 2018. The survival rate of years 1, 2, 3, 4, and 5 after initiation of HD was reported to be 82%, 70%, 62%, 58%, and 55%, respectively (24). Other studies in Brazil in 2020 and Portugal in 2017 have shown similar results (25, 26).
Survival rates in the aforementioned studies are higher than ours. The differences can be, to some extent, related to the centers’ manpower and equipment and preparing appropriate disease management plans according to dialysis adequacy. Frequent pre-dialysis visits of patients, especially the elderly, by a nephrologist for preparedness for vascular access have also been mentioned as an influencing factor in survival rate (27). Finally, as the results of this study showed, although data analysis techniques (i.e., Kaplan–Meier) cannot markedly change the results, they may lead to overestimation.
Some studies indicate that in HD patients, the survival rate is increased with higher socioeconomic status (28). We found a strong relationship between the level of education and mortality of HD patients.
The mortality of HD patients is considered to be higher than the general population and is associated with age so that the survival rate is higher in the young and lower in the elderly patients. Therefore, according to the available data, starting HD at a younger age is preferred and results in a higher survival rate (9, 24, 28, 29). In this study, age at the initiation of HD was also strongly associated with mortality in both cumulative incidence analysis and regression analysis models. Although some studies indicate a relationship between diabetes mellitus and mortality in HD patients, we did not find any relationship between them (12, 29).
Sex has been noted as a significant factor in the survival rate of HD patients (12). In our study, although the cumulative incidence functions of the mortality of females on HD were slightly higher than those of males, it was not statistically significant. Also, in the United States renal data system (USRDS) and Ferreira et al. reports, the analysis did not show a statistical difference between males and females in terms of mortality (9, 26).
Estimates of 5-year survival rates of HD patients reported by Lee et al. in Korea in 2014 and Tuğcu et al. in Turkey in 2018 are fairly similar to ours (12, 29). Some other studies reported lower survival rates for HD patients than our study. Ebrahimi et al. reported a much lower survival rate for 428 HD patients from 2011 to 2016. Survival rates of 1, 2, 3, and 4 years were 74%, 42%, 25%, and 17%, respectively (30). In Montaseri et al. study in 2013, the survival rates for years 1 to 5 after the initiation of HD for 200 patients were 75%, 63%, 50%, 41%, and 23%, respectively (31). Wachterman et al. reported a much lower survival rate for 391 HD patients from 1998 to 2014. The estimated mortality rate at the end of the first year was 54.5% (32). However, it is worth noting that HD patients in most studies with high mortality rates were either elderly or had important underlying diseases such as cardiovascular disease.
5.1. Conclusions
Determination of the survival rate of HD patients is a reliable indicator of the effectiveness of the interventions and can be a significant decision-making and planning tool. The competing risk approach for survival analysis in HD patients reveals the cumulative incidence functions of the event of interest (mortality, for example), and the obtained estimations are more precise than those of direct measurement by conventional methods (i.e., Kaplan-Meier estimator). We conclude that this approach should be introduced and emphasized for survival rate calculations to improve interventions and allocate resources for hemodialysis patients.
Data analysis with competing risk approaches requires the recent versions of special statistical software such as R, SAS, and Stata and the application of programming techniques. Therefore, we recommend that statistical software designers and programmers try to present these techniques in a more user-friendly way to facilitate and expand their use. It is also necessary to prepare a comprehensive database system for HD centers to collect, save, retrieve, and analyze data periodically for more practical patient-oriented planning.
Detection of CKD patients at a younger age, preferably through screening programs and frequent visits by nephrologists, is necessary to prevent the progression of CKD to advanced stages and prepare them for renal replacement therapies, if indicated, to increase the survival rate.
