1. Background
End-stage renal disease (ESRD) would lead to chronic kidney disease (CKD); therefore, early diagnosis and preventive care will help to decrease the speed of ESRD progression (1). Careful monitoring of renal transplant function is essential. Since there are many problems in serial measurements of glomerular filtration rate (GFR) using exogenous substances, such as inulin, chromium 51-ethylenediaminetetraacetic acid (Cr51-EDTA), or technetium 99m-diethylenetriaminepentaacetic acid (TC99m-DTPA), renal transplant function is often estimated using endogenous small molecules, such as serum creatinine concentrations (2). Several renal and non-renal factors can alter serum creatinine concentrations, including tubular secretion, sex, age, physical activity, nutrition, and muscle mass (2, 3). For this reason, to assess the presence of CKD, the alternate approach to assessing GFR should be equation-based creatinine (4).
Guidelines recommended estimated GFR (eGFR)-based creatinine equations, like the Cockcroft-gault (CG) and the abbreviated modification of diet in renal disease (Ab-MDRD) equations. Later in 2012, the kidney disease outcome quality initiative (KDIGO) organization suggested the chronic kidney disease epidemiology collaboration (CKD-EPI) formula. Estimated GFR of creatinine equations is preferred to serum creatinine measurement because serum creatinine measurements are internationally standardized, simple, and inexpensive (3). The CG and MDRD equations have poor accuracy and precision and are not ideal for use in renal transplant populations (4). It was observed that the MDRD equation underestimated the measured GFR for values above 60 mL/min (5-7), which could be misclassified in CKD stages. The shortcoming of creatinine-based equations is well-known for estimating GFR in renal transplant patients (8). Both equations underestimated measured GFR, but CKD-EPI gave more accurate estimates of GFR (9). The main problem with creatinine-based equations is due to intra-individual alterations in serum creatinine concentrations, which has led to the development of several creatinine-based equations whose performance depends on individual characteristics (10). Recent studies have recommended that serum cystatin C usage might lead to better results (4). Sorting CKD progress is conducted by evaluating continuous eGFR equations (11).
Cystatin C is a non-glycosylated protein steadily created by nucleus cells. This protein is freely secreted, does not have reabsorption or tubule secretion, and is not catabolized in the proximal tubule (12, 13). Cystatin C, due to several features, is considered to be an ideal marker of kidney function, and cystatin C measurement is commonly used to evaluate renal function (1). Cystatin C-based EGFR equations have a better diagnostic performance than the creatinine-based GFR equations in renal transplant patients. Various studies have shown a higher correlation between gold standard GFR and eGFR-based cystatin C equations compared to creatinine-based equations in renal transplant patients. Hence, using an accurate and specific equation is important in renal transplant patients (7, 14).
2. Objectives
Measuring creatinine by using the Jaffe method (a non-standard method) is much more accessible and inexpensive than measuring cystatin C in most laboratories in Iran. Creatinine equations were compared with cystatin C equations. Thus, this study aimed to assess an easy approach to evaluate eGFR on occasions when cystatin C is not present in this population with a diagnosis of CKD.
3. Methods
3.1. Study Population
This cross-sectional study was conducted on 58 renal transplant patients (19 to 65 years old). Age, gender, weight, and height were recorded. Inclusion criteria were age less than 18 years. Exclusion criteria were acute rejection during the last three months, hypothyroidism, and hyperthyroidism. They received immunosuppressive drugs, including cyclosporine, tacrolimus, and prednisolone. Written informed consent was obtained from patients. The Ethics Committee of Ahvaz Jundishapur University of Medical Sciences approved this study.
3.2. Determination of Analytes
The serum creatinine concentration was evaluated by the Jaffe method and using an autoanalyzer (Biotecnica BT 3000 Plus, Italy). The levels of cystatin C in serum were measured by an enzyme-linked immunosorbent assay (ELISA; BioVendor, Brno, the Czech Republic) (15, 16) using a spectrophotometric plate reader (Diamed EuroGen, Belgium). The results of cystatin C were obtained as ng/mL that was converted into mg/L; multiply the data by 0.001.
3.3. Calculations of Estimated GFR
The eGFR-based creatinine equations were calculated using three equations, and the eGFR-based cystatin C equations were calculated using five equations according to Supplementary File 1. In these equations, the eGFR unit is presented by mL/min/1.73 m2, except for the CG eGFR equation that corrects for the body surface area (BSA) according to the DuBois-DuBois formula (2):
The unit of serum creatinine is mg/dL, the weight is kg, the age is years, and the BSA is m2. The calculated eGFR was corrected for BSA and normalized to 1.73 m2 (1).
3.4. Statistical Analyses
Mean, and SD were used for continuous variables, and number and percentage were used for categorical variables. Agreement between different eGFR equations was assessed using Bland-Altman plots. The difference between both equations is plotted against the mean of them with bias and 95% limits of agreement for each equation. The efficiency of eGFR equations was assessed by bias, imprecision, and relative bias. Bias would be defined as the mean discrepancy between eGFR cystatin C and eGFR creatinine, and the SD of the mean difference was defined as imprecision. We estimated the relative bias, which is the difference of the average discrepancy among the two results of eGFR cystatin C equations. Accuracy was measured as the ratio of eGFR creatinine within 10% and 30% of the eGFR cystatin C. Concordance among formulas for CKD classification was estimated (proportion of patients designated to the similar grade by two equations). Finally, we assessed the resulting differences in categorizing patients into a division of CKD while using several equations. Data analysis was performed using MedCalc statistical software version 15 (MedCalc software Ltd, Ostend, Belgium) and IBM SPSS version 20 (SPSS Inc, Chicago, IL, USA). P-values less than 0.05 were considered statistically significant.
4. Results
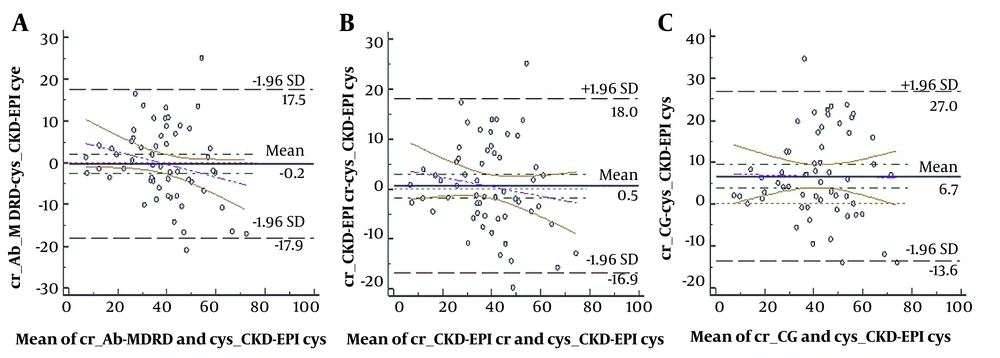
The clinical features of the participants are presented in Table 1. The efficiency of several eGFR equations was estimated by comparing the discrepancy between eGFR-based creatinine and eGFR-based cystatin C in Bland-Altman plots. Figure 1 presents the difference between CKD-EPI eGFR–based creatinine and eGFR-based cystatin C equations (other figures are not included in the article). We choose to use CKD-EPI equations because they are currently recommended by the KDOQI. Contrasted to the CKD-EPI eGFR–based cystatin C equation, the CKD-EPI and CG eGFR-based creatinine overestimated, whereas Ab-MDRD underestimates GFR. Bland-Altman diagrams expressed that eGFR assessed by the Ab-MDRD was the most accurate in contrast to CKD-EPI cystatin C, having an average discrepancy and limits of agreement of - 0.2 (- 17.9, 17.5) (Figure 1A); then, the CKD-EPI creatinine equation showed a bias of + 0.5 (95% CI, - 16.9 to 18; Figure 1B), indicating good agreement. We used CKD-EPI equations because they are currently widely used.
| Variables | Values |
|---|---|
| Age (y) | 42.79 ± 43.5 |
| Sex | |
| Male | 37 (63.8) |
| Female | 21 (36.2) |
| Weight(kg) | 68.03 ± 15.56 |
| Height (cm) | 165.26 ± 10.35 |
| BMI (kg/m2) | 24.86 ± 5.18 |
| Serum creatinine (mg/dL) | 2.27 ± 1.41 |
| Serum cystatin C (mg/L) | 2.045 ± 1.09 |
| eGFR creatinine (mL/min/1.73 m2) | |
| CG * | 45.30 ± 15.75 |
| Ab-MDRD | 38.43 ± 13.87 |
| CKD-EPI | 39.12 ± 14.63 |
| eGFR cystatin C (mL/min/1.73 m2) | |
| Le Bricon | 47.9 ± 14.41 |
| Filler-lepage | 48.42 ± 17.58 |
| CKD-EPI | 38.6 ± 15.94 |
| Hoek | 40.9 ± 14.84 |
| Rule (renal transplant recipients) | 39.74 ± 14.84 |
Features of the Patients (N = 58) a
Table 2 presents the classification of patients in various CKD categories based on different equations. Most eGFR in patients were in stages 2 and 3 of CKD
| CKD Stages | Values | |||||
|---|---|---|---|---|---|---|
| Stage 1 (≥ 90) | Stage 2 (60 - 90) | Stage 3a (45 - 60) | Stage 3b (30 - 45) | Stage 4 (15 - 30) | Stage 5 (< 15) | |
| eGFR creatinine (mL/min/1.73 m2) | ||||||
| Ab-MDRD | 0 (0) | 2 (3.4) | 15 (25.9) | 29 (50) | 7 (12.1) | 5 (8.6) |
| CG | 0 (0) | 10 (17.2) | 21 (36.2) | 18 (31) | 6 (10.3) | 3 (5.2) |
| CKD-EPI | 0 (0) | 5 (8.6) | 13 (22.4) | 27 (46.6) | 8 (13.8) | 5 (8.6) |
| eGFR cystatin C (mL/min/1.73 m2) | ||||||
| Le Bricon | 0 (0) | 13 (22.4) | 24 (41.4) | 15 (25.9) | 6 (10.3) | 0 (0) |
| Filler-Leapage | 0 (0) | 14 (24.1) | 22 (37.9) | 12 (20.7) | 7 (12.1) | 3 (5.2) |
| CKD-EPI | 0 (0) | 4 (6.9) | 15 (25.9) | 23 (39.7) | 12 (20.7) | 4 (6.9) |
| Hoek | 0 (0) | 6 (10.3) | 14 (24.1) | 24 (41.4) | 11 (19) | 3 (5.2) |
| Rule (renal transplant recipients) | 0 (0) | 5 (8.6) | 14 (24.1) | 24 (41.4) | 12 (20.7) | 3 (5.2) |
Distribution of Renal Transplant Patients According to the Chronic Kidney Disease Staging a
4.1. The 10% and 30% Accuracy of the eGFR Creatinine and eGFR Cystatin C
Table 3 shows the comparing bias, imprecision, and relative bias of creatinine equations vs. cystatin C equations. The comparison of CKD-EPI cystatin C and Ab-MDRD showed a small overall bias (- 0.2 mL/min/1.73 m2). The quantity of the relative bias was equal to the absolute bias. The results showed that with reference to CKD-EPI eGFR-based cystatin C, Ab-MDRD illustrated the lowermost instability (- 0.5%). With reference to CKD-EPI cystatin C, the imprecision of the equations was approximately similar; therefore, we can demonstrate the slight difference of those methods in comparison to cystatin C equations. Ab-MDRD and CKD-EPI creatinine are still better than CG.
| eGFR Cystatin C | eGFR Creatinine; No. (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Ab-MDRD | CKD-EPI | CG | |||||||
| Bias (Imprecision), Relative Bias | 10% | 30% | Bias (Imprecision), Relative Bias | 10% | 30% | Bias (Imprecision), Relative Bias | 10% | 30% | |
| CKD-EPI | - 0.2 (1.19), - 0.5 | 25.9 | 81 | 0.5 (1.17), 1.3 | 31 | 79.3 | 6.7(1.36), 17.4 | 27.6 | 65.5 |
| Hoek | - 2.5 (1.05), - 6.1 | 56.9 | 79.8 | - 1.8 (1.06), - 4.4 | 32.8 | 86.2 | 4.4(1.27), 10.8 | 36.2 | 72.4 |
| Filler-Leapage | - 10 (1.24), - 20.7 | 24.1 | 72.4 | - 9.3 (1.23), - 19.2 | 20.7 | 72.4 | - 3.1(1.41), - 6.4 | 22.4 | 84.5 |
| Le Bricon | - 9.5 (1.03), - 19.8 | 22.4 | 72.4 | - 8.8 (1.04), - 18.4 | 27.6 | 70.7 | - 2.6(1.25), - 5.4 | 24.1 | 84.5 |
| Rule (renal transplant recipients) | - 1.3 (1.06), - 3.3 | 31 | 79.3 | - 0.6 (1.07), - 1.5 | 34.5 | 79.3 | 5.6(1.29), 14.1 | 36.2 | 72.4 |
The 10% and 30% accuracy showed acceptable results for the equations (see Table 4). Accuracy with reference to cystatin C equations was almost similar, except for the CG equation. Among these equations, the best of all performed Hoek vs. CKD-EPI creatinine exhibited the highest 30% accuracy (86.2% of patients with < 30% difference between them). Limiting the agreement range to 10% drastically decreased accuracy.
The concordance between both equations is evaluated in Table 4. The lowest concordance was found in eGFR Ab-MDRD vs. eGFR Filler-Leapage (0.683), eventuating a higher stage for most of the patients.
| CKD-EPI | Filler-Leapage | Hoek | Le Bricon | Rule | |
|---|---|---|---|---|---|
| Ab-MDRD | 0.817 (0.714 - 0.886) | 0.683 (0.559 - 0.778) | 0.834 (0.737- 0.897) | 0.69 (0.565 - 0.784) | 0.838 (0.743 - 0.9) |
| CG | 0.721 (0.585 - 0.818) | 0.779 (0.658 - 0.861) | 0.77 (0.646 - 0.854) | 0.788 (0.670 - 0.867) | 0.745 (0.615 - 0.836) |
| CKD-EPI | 0.83 (0.731 - 0.895) | 0.713 (0.591 - 0.803) | 0.844 (0.75 - 0.904) | 0.716 (0.594 - 0.806) | 0.845 (0.752 - 0.905) |
Concordance (95% CI) for Estimated Glomerular Filtration Rate-Serum Creatinine vs. Estimated Glomerular Filtration Rate-Cystatin C Equations a
4.2. Misclassification of CKD Stages by the All Equations
The classification of patients according to the estimated renal function of a 60-mL/min/1.73-m2 cutoff ratio was investigated (Table 5). The Hoek and CKD-EPI creatinine equations classified most patients correctly (94.8%), followed by CKD-EPI cystatin C/Ab-MDRD and Rule/CKD-EPI creatinine (93.1%). All equations had high accuracy (range, 75.8% - 94.8%) for the diagnosis of CKD. However, Ab-MDRD and CKD-EPI eGFR creatinine exhibited the highest accuracy (93.1%). Finally, our finding suggested that Ab-MDRD and CKD-EPI eGFR creatinine might be the best-performing equation due to the accurate classification of the CKD stage in a cutoff of 60 mL/min/1.73 m2.
| eGF R Creatinine | eGFR Cystatin C | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CKD-EPI | Filler-Leapage | Le Bricon | Hoek | Rule | |||||||||||
| < 60 | ≥ 60 | % | < 60 | ≥ 60 | % | < 60 | ≥ 60 | % | < 60 | ≥ 60 | % | < 60 | ≥ 60 | % | |
| Ab-MDRD | 93.1 | 75.8 | 77.6 | 89.6 | 91.4 | ||||||||||
| 53 (91.4) | 3 (5.2) | 43 (74.1) | 13 (22.4) | 44 (75.9) | 12 (20.7) | 51 (87.9) | 5 (8.6) | 52 (89.7) | 4 (6.9) | ||||||
| 1 (1.7) | 1 (1.7) | 1 (1.7) | 1 (1.7) | 1 (1.7) | 1 (1.7) | 1 (1.7) | 1 (1.7) | 1 (1.7) | 1 (1.7) | ||||||
| CG | 86.2 | 79.3 | 77.6 | 86.2 | 84.5 | ||||||||||
| 47 (81) | 1 (1.7) | 4 (69) | 8 (13.8) | 40 (69) | 8 (13.8) | 46 (79.3) | 2 (3.4) | 46 (79.3) | 2 (3.4) | ||||||
| 7 (12.1) | 3 (5.2) | 4 (6.9) | 6 (10.3) | 5 (8.6) | 5 (8.6) | 6 (10.3) | 4 (6.9) | 7 (12.1) | 3 (5.2) | ||||||
| CKD-EPI | 91.3 | 81 | 82.8 | 94.8 | 93.1 | ||||||||||
| 51 (87.9) | 2 (3.) | 43 (74.1) | 10 (17.2) | 44 (75.9) | 9 (15.5) | 51 (87.9) | 2 (3.4) | 51 (87.9) | 2 (3.4) | ||||||
| 3 (5.2) | 2 (3.4) | 1 (1.7) | 4 (6.9) | 1 (1.7) | 4 (6.9) | 1 (1.7) | 4 (6.9) | 2 (3.4) | 3 (5.2) | ||||||
Misclassification of Patients at the Estimated Glomerular Filtration Rate in a Cutoff of 60 mL/min/1.73 m2
5. Discussion
Renal dynamic imaging that uses exogenous substances is still not readily available in most of Iran’s clinical settings. Glomerular filtration rate estimation using creatinine as an endogenous marker is currently used to assess renal function in renal transplant recipients (17). Categorizing various CKD grades connotes several clinical intentions. Therefore, eGFR is essential for discovering and classifying CKD, characterizing medicine doses, and optimizing the doses of multiple medicines for renal function (18). In routine clinical operations, measuring eGFR-based creatinine is a standard method to estimate renal function (19, 20). Meanwhile, eGFR-based serum creatinine is unreliable due to endogenous influences of age, gender, muscle mass, and tubular secretion of creatinine (17). Therefore, an appropriate renal function estimation equation is necessary to improve the therapeutic efficacy and prevent drug side effects (21).
Studies have suggested that when renal function decreases, the detection of cystatin C is increased more significantly than creatinine in renal transplant patients (2). Since the assessment of serum creatinine is inexpensive and available, it could be evaluated immediately. On the other hand, cystatin C is not always accessible because of its high cost and complex procedure (11); also, cystatin C evaluation is not a routine assay in Iran and worldwide (3). This study aimed to identify an appropriate eGFR equation in the renal transplant population in the south of Iran (Khuzestan).
In this study, we performed different eGFR-based creatinine equations compared to eGFR-based cystatin C equations in renal transplant recipients. A variety of essential agents that influence the result of eGFR-based creatinine equations (Ab-MDRD, CKD-EPI, and CG) would deviate outputs in contrast with results obtained from eGFR-based cystatin C equations. On the other hand, the results of eGFR are easily over-evaluated by the CG formula than by the Ab-MDRD and CKD-EPI equations in renal transplant patients. We observed a strong correlation between eGFR creatinine and eGFR cystatin C. As shown by high P30 values, this could account for the powerful performance of these equations in this population. Bias was significantly reduced in Ab-MDRD and then CKD-EPI equations and provided more reliable eGFRs in this population. Similar to our study, Salvador et al. also confirmed that the Ab-MDRD equation was the most accurate of the creatinine equations in renal transplant patients (7).
In the present study, Bland-Altman plots showed that Ab-MDRD and CKD-EPI eGFR creatinine against CKD-EPI eGFR cystatin C had similar low limits of agreement, demonstrating the higher agreement of these equations. Al-Wakeel demonstrated that the CKD-EPI-based creatinine formula was the most proper, precise, and accurate in evaluating GFR compared to other eGFR equations (1).
In the lack of an accurate equation, misclassification of renal transplant patients can lead to the application of incorrect diagnosis and treatment. The precise classification of the CKD stage facilitates the successful management of these patients (6). After classifying transplanted patients in CKD stages according to the stage of kidney disease, we found that the percentage of agreement between eGFR of serum cystatin C and creatinine is greater than 75.6. On the other hand, due to the lack of the exogenous marker to measure GFR, we could not measure better kidney function in renal transplant recipients.
Our study showed a small difference between the Ab-MDRD and CKD-EPI eGFR creatinine formulas compared to CKD-EPI eGFR cystatin C in a cutoff of 60 mL/min/1.73 m2 in CKD staging. A high level of agreement between the two eGFR assessments for individual patients may often lead to appropriate prescribing programs and correct regulation of CKD. Because the values of serum creatinine in renal transplant patients vary significantly depending on the severity of CKD, the criteria of the serum creatinine values for the CKD‐EPI equation should be modulated. Among these equations, the results of CKD classification measured by the MDRD equation are the most optimistic.
5.1. Conclusions
Since cystatin C measurements are not available in all laboratories, we suggested Ab-MDRD and CKD-EPI equations that have a closer relationship with the CKD-EPI cystatin C equation in kidney transplant patients. Therefore, this study shows the importance of conducting an appropriate survey to establish a novel equation and modified factors to accurately assess renal function in the Iranian population. Also, it is essential to investigate the effects of various factors on the cystatin C metabolism in the Iranian population so that a new Iranian eGFR equation derived from cystatin C and creatinine is created in a large group of several centers in renal transplant patients. Further studies are necessary to better determine the best equation for estimating GFR in Iranian renal transplant patients. On the other hand, it is recommended that the usage of serum creatinine and cystatin C to compensate for biases should be replaced by combined equations that depend on single factors.
5.2. Study Limitations
This study has some limitations. Besides having a small sample size, the reference method for measuring GFR was not used for comparison. Also, serum creatinine was assessed using the Jaffe method, which is not standardized but is a routine approach. In addition, serum cystatin C was analyzed using an ELISA method because it is a routine method in diagnostic laboratories. Finally, it is a single-center study that is ethnically narrow (south of Iran).