A Comparison of Estimated GFRs Based on Formulas of Serum Cystatin C and Serum Creatinine

Nouraddin Mousavinasab; Mojgan Jalalzadeh

doi:10.5812/numonthly.46917

Nephro-Urology Monthly

Current Issue All Issues In Press Accepted Manuscripts Search

Journal Information Boards and Committees Indexing and Listing Sources Journal Metrics Open Peer Review (OPR)Publication Ethics and Malpractice Statement Contact Us Support Reviewer and AE Registration Form

APC

Authors Guide Submit Manuscript

https://doi.org/10.5812/numonthly.46917

A Comparison of Estimated GFRs Based on Formulas of Serum Cystatin C and Serum Creatinine

Author(s):

Nouraddin Mousavinasab¹,

Mojgan Jalalzadeh^2,*

1Department of Biostatistics, Mazandaran University of Medical Sciences, Sari, IR Iran

2Department of Nephrology, Loghman Hakim Hospital, Shahid Beheshti University of Medical Sciences, Tehran, IR Iran

Nephro-Urology Monthly:Vol. 9, issue 3; e46917

Published online:May 07, 2017

Article type:Research Article

Received:Feb 22, 2017

Accepted:Apr 07, 2017

How to Cite:Nouraddin MousavinasabMojgan JalalzadehA Comparison of Estimated GFRs Based on Formulas of Serum Cystatin C and Serum Creatinine.Nephro-Urol Mon.9(3):e46917.https://doi.org/10.5812/numonthly.46917.

Abstract

Background:

Serum cystatin C has been identified as a marker for the estimation of glomerular filtration rate (GFR). Although this marker is more sensitive than creatinine, it is too expensive and not available in all laboratories. In this study, we compared cystatin C-based equations with creatinine-based formulas to select the most precise creatinine-based formula for estimating GFR in patients with chronic kidney disease (CKD).

Methods:

120 patients with CKD were enrolled in this cross-sectional study. The patients were divided into groups according to BMI (< 25, 25 - 29.9, and ≥ 30) and age (≤ 40, 41 - 60, and ≥ 60). The patients’ GFRs were estimated and analyzed by using three creatinine-based equations (modification of diet in renal disease (MDRD), abbreviated MDRD, and Cockcroft and Gault (C-G)) and five cystatin C-based equations (Filler, Le Bricon, Rule, Hoek, and Larsson).

Results:

The mean age of patients was 56.4 ± 16.4 years. The mean of GFRs using C-G, MDRD, and abbreviated MDRD formulas were 36.2 ± 14.3, 32.6 ± 11.4, and 32.4 ± 11.3 mL/min/1.73 m², respectively. The mean of GFRs using Filler, Le Bricon, Larsson, Rule, and Hoek equations were 54.7 ± 20.1, 53.0 ± 15.7, 43.6 ± 18.5, 45.1 ± 17.2, and 46.2 ± 16.2 mL/min/1.73 m², respectively. The closest correlation was observed between GFRs generated by Abbreviated MDRD and cystatin C-based equations (P < 0.001, r: 0.4, R²: 0.16). Differences in GFR estimation between cystatin C-based equations and C-G equation were lower at higher BMI levels (P: 0.004 - 0.01, F: 4.5 - 6.7). Differences in GFR estimation between cystatin C-based equations and C-G as well as MDRD equations were greater in older patients (P: 0.01 - 0.04, F: 3.2 - 4.1).

Conclusions:

GFRs estimated by Abbreviated MDRD equation are closer to GFRs estimated by cystatin C equations regardless of patients’ BMI in CKD subjects.

Keywords

Glomerular Filtration Rate (GFR)

Creatinine

Cystatin C

Chronic Kidney Disease (CKD)

Body Mass Index (BMI)

1. Background

The best method to assess renal function is measuring the glomerular filtration rate (GFR) (1). Chronic kidney disease (CKD) patients are classified into stages 1-5 based on GFR. Inulin has been used as a gold standard indicator for measuring GFR (2). Other substances used as filtration markers include 125 Iothalamate, chromium-51 ethylenediaminetetraacetic acid, and Iohexol (3). However, these substances are not often used because they are time-consuming, expensive, and difficult to process (4). Ideally, GFR should be determined with an accurate, inexpensive method. Estimation of GFR can be done using Modification of Diet in Renal Disease (MDRD), abbreviated MDRD, or Cockcroft and Gault (C-G) equations (5), which can present different results. Differences in results are due to the standardization of analytical techniques, the rate of production and tubular secretion of creatinine (6).

Furthermore, creatinine concentration is not only affected by GFR but also affected by other factors such as diet, muscle mass, gender, and age.

The best marker to estimate GFR should be a product that is produced continuously in the body and excreted by the kidney via free glomerular filtration without tubular absorption or secretion (7).

Cystatin C has been proposed as a new filtration marker to substitute creatinine, and it is very sensitive to changes in GFR (8). Cystatin C is a low molecular-weight basic protein (13 kDa) that is produced at a constant rate by all nucleated cells of the body and freely filtered by the glomeruli of the kidney without tubular secretion and absorption (8).

Some investigators have suggested that serum cystatin C has advantages over serum creatinine to estimate GFR as it is not affected by age, gender, muscle mass, drugs, and diet (9, 10). However, some other investigators have questioned this idea (11). To determine GFR based on serum cystatin C, several equations such as Larsson, Hoek, Filler, Le Bricon, and Rule have been proposed (12-16).

Studies have shown that BMI is related to the serum levels of cystatin C (17-19). The mechanism of this association is unclear, but experimental evidence suggests that adipocyte tissues secrete large amounts of cystatin C, which can lead to the increased levels of serum cystatin C in obese individuals with high BMI (20). According to this assumption, estimated GFRs based on cystatin C formulas in obese cases may be different from those estimated by the gold standard. Whereas, in high BMI cases, it is expected that the result of GFR estimation by creatinine-based formulas be different from that of cystatin C-based equations.

In this study, we compared cystatin C-based equations with creatinine based formulas to identify the most precise formula to estimate GFR in Iranian population diagnosed with CKD. Also, the relation of these formulas results with patients BMI, age, and sex is presented.

2. Methods

In this cross-sectional study, we investigated 120 patients with CKD, whose 3-month baseline GFR was less than 60 mL/min per 1.73 m².

Our exclusion criteria were pregnancy, liver cirrhosis, hypothyroidism, hyperthyroidism, or administration of any medication interfering with creatinine tubular secretion. Each subject gave his/her informed consent.

Non-fasting morning blood samples were taken and analyzed for serum creatinine, urea, and cystatin C. The Jaffe method was used to measure creatinine with a Boehringer Mannheim/Hitachi 747 analyzer. Serum cystatin C levels were determined with the Human cystatin C ELISA kit using Bio Vendor Laboratory Medicine, AS. The calibrated creatinine was used in all analyses involving the MDRD equations. GFR was estimated using the creatinine-based MDRD, Abbreviated MDRD, and C-G equations (21) as well as the cystatin C-based Le Bricon (12), Filler (13), Hoek (14), Larsson (15), and Rule (16) equations per surface area of 1.73 m², as shown in Table 1.

Table 1. Five Cystatin C-Based and Three Creatinine-Based Estimates of GFRs

Equation	Formula, mL/min/1.73 m²
Cystatin C-based
Filler	Log (GFR) = 1.962 + (1.123 × log (1/cystatin C))
Le Bricon	GFR = (78 × (1/cystatin C)) + 4
Hoek	GFR = -4.32 + (80.35 × 1/cystatin C)
Larsson	GFR = 77.24 × cystatin C^-1.2623
Rule	GFR = 76.6 × cystatin C^-1.16
Creatinine-based
MDRD	GFR = 170 × creatinine^-0.999 × age^-0.176 × blood urea nitrogen^-0.170 × albumin^0.318 × (0.762 for women) ×(1.180 for African-Americans)
Abbreviated MDRD	GFR = 186 × creatinine^-1.154 × age^-0.203 × (0.742 for women) × (1.212 for African-Americans)
Cockcroft and Gault	GFR = ((140 - age) × body weight)/(creatinine × 72) × (0.85 for women)

Five Cystatin C-Based and Three Creatinine-Based Estimates of GFRs

For analysis, the patients were divided into three categories according to their BMI as: normal weight (BMI: 18.5 to < 25), overweight (BMI: 25 - 30), and obese (BMI > 30). They were also divided into three groups according to their age as: under 40 years, 40 to 60 years, and more than 60 years.

2.1. Statistical Analyses

SPSS software (version 20.0) was used to analyze data. The normality of the distribution of variables was checked by one- sample Kolmogorov-Smirnov test. Pearson correlation coefficient was used to examine relations among quantitative variables. Linear regression models were used to determine relations among different methods of GFR assessment. Chi-square was used to compare qualitative variables in groups, two sample t-test to compare quantitative variables between two groups, and one-way analysis of variance (ANOVA) to compare quantitative variables between multiple groups. Student’s t-test was used to evaluate each parameter in female and male groups. Spearman rank correlation, Mann Whitney U test, and Kruskal Wallis test were used for variables with non-normal distribution as appropriate non-parametric tests. A P value less than 0.05 was considered significant.

3. Results

Out of 120 patients, 45.8% (55) were female and 54.2% were male (65). The mean age of patients was 56.4 ± 16 years. The patients’ height ranged from 143 to 180 cm and the mean height was 163 ± 8 cm. The mean weight of patients was 68.2 ± 11 kg ranging from 37 to 95 kg. The mean BMI of the patients was 25.6 ± 3 kg/m², mean creatinine was 2.2 ± 0.6 mg/dL, and mean cystatin C was 1.7 ± 0.5 mg/L.

The other characteristics of patients are shown in Table 2.

Table 2. Demographic Characteristics of the Patients^a

Characteristics	Value
Male	55 (45.8)
Female	65 (54.2)
Age, y	56.41 ± 16.4
Hight, cm	163.04 ± 8.4
Weight, Kg	68.22 ± 11.7
BMI, kg/m²	25.65 ± 3.9
Serum creatinine, mg/dL	2.20 ± 0.65
Serum cystatin C, mg/L	1.73 ± 0.51
Serum Albumin, g/dL	4.55 ± 0.47
BUN, mg/dL	41.76 ± 18.3

Demographic Characteristics of the Patients^a

The mean values of estimated GFRs by three creatinine-based formulas (C-G, MDRD, and abbreviated MDRD) and five cystatin C-based equations (Filler, Le Bricon, Larsson, Rule, and Hoek) are demonstrated in Table 3. Also, the frequencies of different CKD stages according to the GFR estimating formulas are shown in Table 3.

Table 3. Demographic Characteristics of the Patients (Estimated GFRs by Creatinine-Based and Cystatin C-Based Equations)^a

Variables	Value	Stage 1	Stage 2	Stage 3	Stage 4	Stage 5
Cockcroft and Gault	36.26 ± 14.33	0	7 (5.8)	72 (60)	36 (30)	5 (4.2)
Abbreviated MDRD	32.44 ± 11.38	0	1 (0.8)	62 (51.7)	53 (44.2)	4 (3.3)
MDRD	32.69 ± 11.44	0	2 (1.7)	63 (52.5)	52 (43.3)	3 (2.5)
Rule	45.12 ± 17.27	3 (2.5)	12 (10)	91 (75.8)	14 (11.7)	0
Larsson	43.69 ± 18.52	3 (2.5)	9 (7.5)	91 (75.8)	17 (14.2)	0
Hoek	46.22 ± 16.26	3 (2.5)	13 (10.8)	90 (75)	14 (11.7)	0
Le Bricon	53.06 ± 15.78	4 (3.3)	19 (15.8)	92 (76.7)	5 (4.2)	0
Filler	54.78 ± 20.18	7 (5.8)	21 (17.5)	83 (69.2)	9 (7.5)	0

Demographic Characteristics of the Patients (Estimated GFRs by Creatinine-Based and Cystatin C-Based Equations)^a

3.1. Correlation Between Creatinine-Based and Cystatin C-Based Equations for GFR Estimation

There was a strong significant relationship among GFR values estimated by three creatinine-based formulas (r: 0.74 to 0.98, P value < 0.0001). Also, the correlation coefficient showed that there are significant correlations among all the five cystatin C-based GFRs estimating equations (r: 0.99 to 1, P value < 0.0001).

In addition, based on the results, all of the creatinine-based and cystatin C-based equations had a significant correlation for GFR estimation (P value < 0.001), as demonstrated in Table 4.

Table 4. Correlation Among Creatinine-Based and Cystatin C-Based Equations for for GFR Estimation

Cystatin C-Based Equations	Creatinine-Based Equations
	Cockcroft and Gault		Abbreviated MDRD		MDRD
	r	P value	r	P value	r	P value
Rule	0.384	< 0.001	0.400	< 0.001	0.383	< 0.001
Larsson	0.380	< 0.001	0.396	< 0.001	0.379	< 0.001
Hoek	0.391	< 0.001	0.407	< 0.001	0.390	< 0.001
Le Bricon	0.391	< 0.001	0.407	< 0.001	0.390	< 0.001
Filler	0.386	< 0.001	0.402	< 0.001	0.375	< 0.001

Correlation Among Creatinine-Based and Cystatin C-Based Equations for for GFR Estimation

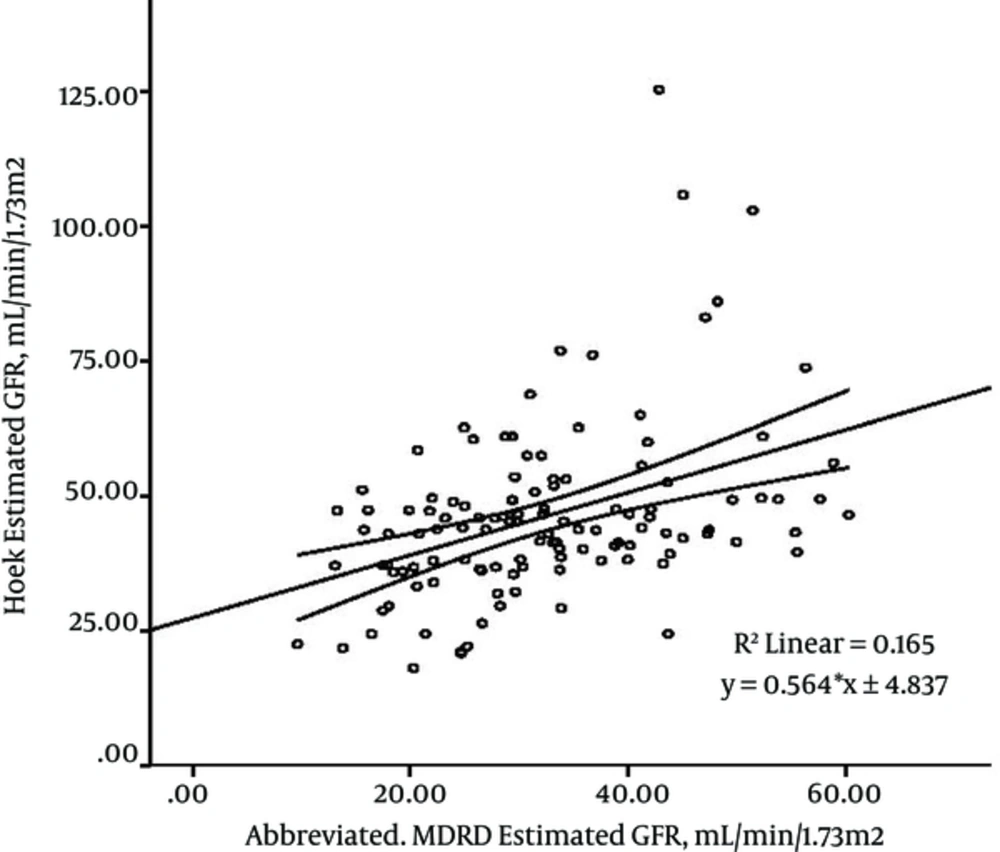
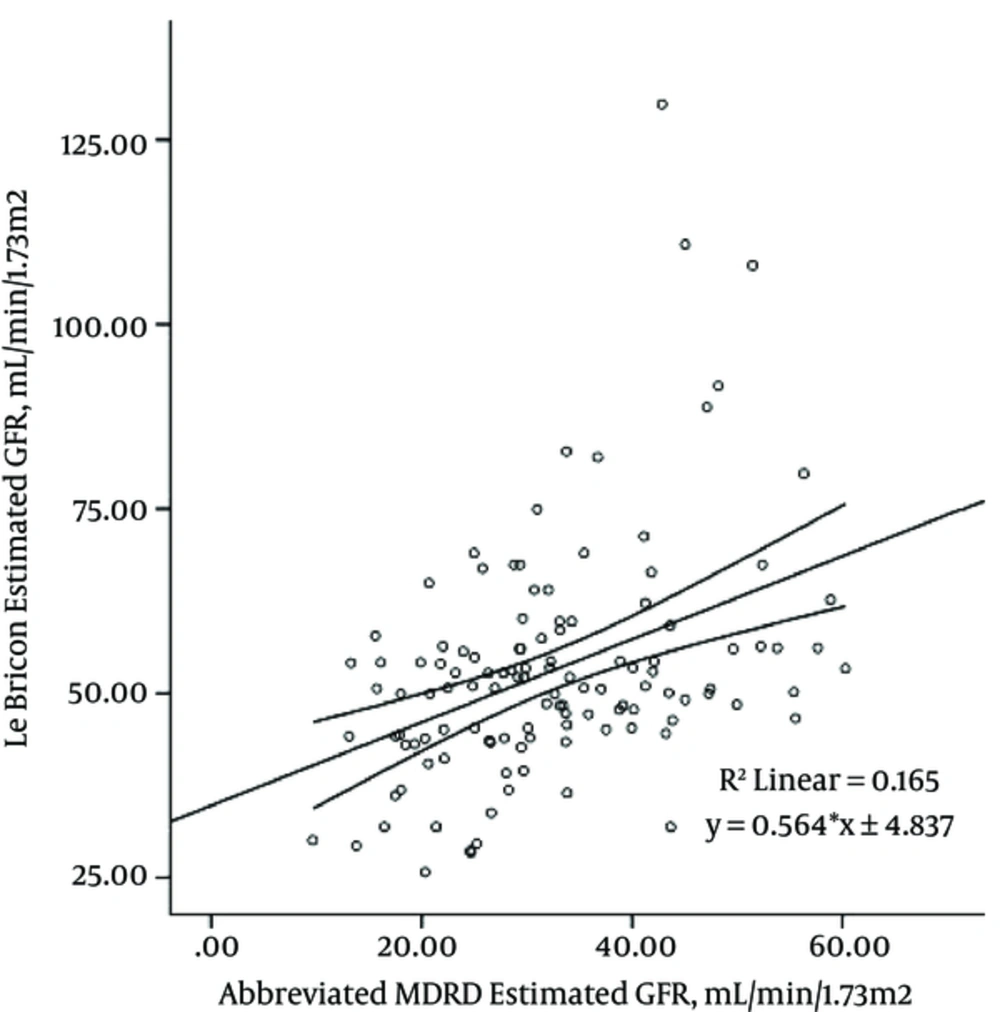
The linear regression model of creatinine-based formulas and cystatin C-based equations for GFR estimation indicated that the most significant correlations were between abbreviated MDRD formula and Hoek and Le Bricon equations (r: 0.40), as shown in Figure 1 and 2.

Figure 1.

Correlation Between Abbreviated MDRD and Hoek Formulas for GFR Estimation

Figure 2.

Correlation between Abbreviated MDRD and Le Bricon formulas for GFR estimation

As shown in Figure 1 and 2, the estimated GFRs by abbreviated MDRD are able to predict 16% of variances of the Hoek-estimated GFRs and Le Bricon-estimated GFRs (R square: 0.165).

The result of the study showed that there is a significant correlation between serum cystatin C and serum creatinine (r: 0.48, P value < 0.001). On the other hand, there was not any significant correlation between BMI and creatinine (r: -0.01, P value: 0.91,) and cystatin C (r: -0.009, P value: 0.92).

3.2. Association Between Creatinine-Based and Cystatin C-Based Equations for GFR Estimation and Their Relationship with BMI, Age, and Sex

The correlation between BMI and GFRs estimated by creatinine based-formulas is demonstrated in Table 5. Mean GFR estimated by C-G equation was higher in the cases with higher amount of BMI (P value < 0.001). However, changes in BMI did not show any significant relationship with the mean GFR estimated by other formulas (P value: 0.9).

Table 5. Association Between Creatinine-Based and Cystatin C-Based Equations for for GFR Estimation and Their Relationship with BMI, Age, and Gender

Variables	Body Mass Index				Age, y				Gender
	Normal Weight	Over weight	Obesity	P Value	< 40	40 - 60	> 60	P Value	Male	Female	P Value
Cockcroftand Gault	30.5 ± 11.1	37.9 ± 13.3	47.1 ± 18.0	< 0.001	43.2 ± 15.2	41.9 ± 14.9	29.5 ± 10.1	< 0.001	31.9 ± 11.7	39.9 ± 15.3	0.003
Abbreviated MDRD	33.3 ± 12.2	32.1 ± 10.4	33.5 ± 12.2	0.8	35.7 ± 13.3	32.4 ± 11.7	31.2 ± 10.2	0.6	26.6 ± 8.8	37.3 ± 11.1	< 0.001
MDRD	32.4 ± 12.2	32.8 ± 10.6	33.0 ± 11.9	0.9	36.5 ± 13.8	32.1 ± 11.7	31.6 ± 10.0	0.5	27.2 ± 9.1	37.3 ± 11.2	< 0.001
Rule	44.8 ± 18.9	45.1 ± 13.7	45.8 ± 22.2	0.9	44.0 ± 9.6	49.4 ± 22.7	42.1 ± 13.6	0.4	45.0 ± 17.6	45.2 ± 17.1	0.8
Larsson	43.4 ± 20.3	43.6 ± 14.6	44.6 ± 23.7	0.9	42.4.2 ± 10.0	48.3 ± 24.7	40.5 ± 14.2	0.4	43.6 ± 19.0	43.8 ± 18.2	0.8
Hoek	45.8 ± 17.8	46.4 ± 12.9	46.7 ± 20.9	0.9	45.4 ± 9.3	50.2 ± 21.0	43.4 ± 13.3	0.4	46.1 ± 16.4	46.3 ± 16.2	0.8
Le Bricon	52.6 ± 17.3	53.2 ± 12.5	53.7 ± 20.3	0.9	52.3 ± 9.1	56.9 ± 20.4	50.3 ± 12.9	0.4	52.9 ± 15.9	53.1 ± 15.7	0.8
Filler	54.3 ± 22.1	54.8 ± 16.0	55.6 ± 25.9	0.9	53.6 ± 11.3	59.7 ± 26.5	51.2 ± 16.0	0.4	54.6 ± 20.5	54.8 ± 19.9	0.8

Association Between Creatinine-Based and Cystatin C-Based Equations for for GFR Estimation and Their Relationship with BMI, Age, and Gender

The results showed that increases in age significantly reduce the mean GFR generated by C-G formula (P value < 0.0001). However, changes in age did not show any significant correlation with the mean GFR estimated by other formulas.

A relation was detected between GFRs from creatinine-based formulas and gender, but such a relation was not found for GFRs from cystatin C-based equations.

3.3. The Prevalence of Stages 3 - 4 CKD by Using Creatinine-Based and Cystatin C-Based Formulas, and Their Relation with BMI, Age, and Sex

As presented in Table 6, the prevalence of stages 3-4 CKD is significantly lower in patients with higher BMI than patients with lower BMI (P value: 0.005) by using C-G formula, while no appreciable difference was seen between BMI groups using other formulas. In addition, the prevalence of stages 3 - 4 CKD, estimated by C-G and MDRD formulas, was affected significantly by age (P value: 0.03 and 0.008, respectively). Also, there was no significant sex difference in the prevalence of stages 3 - 4 CKD.

Table 6. The Prevalence of Stages 3 - 4 CKD by Using Creatinine-Based and Cystatin C-Based Formulas, and Their Relation with BMI , Age, and Sex^a

Variables	Body Mass Index, kg/m²				Age, y				Sex
	Normal Weight (18.5 - 24.9)	Over weight (25.0 - 29.9)	Obesity (≥ 30.0)	P value	< 40	40 - 60	> 60	P value	Female	Male	P value
No.	50	52	18		21	44	55		55	65
Cockcroft and Gault	49 (98)	50 (96.2)	14 (77.8)	0.005	18 (85.7)	40 (90.9)	55 (100)	0.030	54 (98.2)	59 (90.8)	0.12
Abbreviated MDRD	49 (98)	52 (100)	18 (100)	0.49	20 (95.2)	44 (100)	55 (100)	0.093	55 (100)	64 (98.5)	1.0
MDRD	48 (96)	52 (100)	18 (100)	0.24	19 (90.5)	44 (100)	55 (100)	0.008	55 (100)	63 (96.9)	1.0
Rule	44 (88)	45 (86.5)	16 (88.9)	0.95	20 (95.2)	36 (81.8)	49 (89.1)	0.27	50 (90.9)	55 (84.6)	0.41
Larsson	45 (90)	47 (90.4)	16 (88.9)	0.98	20 (95.2)	37 (84.1)	51 (92.7)	0.24	50 (90.9)	58 (89.2)	0.49
Hoek	43 (86)	45 (86.5)	16 (88.9)	0.95	19 (90.5)	36 (81.8)	49 (89.1)	0.48	49 (89.1)	55 (84.6)	0.83
Le Bricon	39 (78)	44 (84.6)	14 (77.8)	0.65	16 (76.2)	33 (75)	48 (87.3)	0.25	46 (83.6)	51 (78.5)	0.49
Filler	39 (78)	41 (78.8)	12 (66.7)	0.55	16 (76.2)	31 (70.5)	45 (81.8)	0.41	43 (78.2)	49 (75.4)	0.83

The Prevalence of Stages 3 - 4 CKD by Using Creatinine-Based and Cystatin C-Based Formulas, and Their Relation with BMI , Age, and Sex^a

3.4. Difference Between Creatinine-Based and Cystatin C-Based Formulas for GFR Estimation and Their Correlation with BMI, Age, and Sex

The differences between GFRs estimated by cystatin C-based equations and those estimated by C-G equation are lower at higher BMI levels (P value: 0.004 - 0.01), as shown in Table 7.

Table 7. Difference Between Creatinine-Based and Cystatin C-Based Formulas for GFR Estimation and Their Correlation with BMI, Age, and sex

Variables	Body Mass Index, kg/m²				AGE, y				Sex
Differences between cystatin-based and creatinine-based equations	Normal Weight (18.5 - 24.9)	Over weight (25.0 - 29.9)	Obesity (≥ 30.0)	P Value	< 40	40 - 60	> 60	P Value	Female	Male	P Value
Rule-Cockcroft-Gault	14.20	7.23	-1.20	0.004	0.79	8.09	12.58	0.031	13.11	5.3	0.015
Larsson-Cockcroft-Gault	12.8	5.70	-2.24	0.007	0.86	7.01	10.94	0.045	11.6	3.8	0.021
Hoek-Cockcroft-Gault	22.09	15.30	6.47	0.002	9.02	15.58	20.76	0.018	21.06	13.2	0.01
Le Bricon-Cockcroft-Gault	22.09	15.30	6.47	0.002	9.02	15.58	20.76	0.018	21.06	13.2	0.01
Filler-Cockcroft-Gault	23.79	16.94	8.52	0.01	10.32	18.45	21.73	0.078	22.7	14.9	0.03
Rule-abbreviated MDRD	12.44	13.02	12.32	0.98	8.31	17.02	10.87	0.073	18.3	7.8	<0.001
Larsson-abbreviated MDRD	11.04	11.49	11.08	0.99	6.65	15.95	9.23	0.068	16.9	6.4	0.001
Hoek-abbreviated MDRD	13.48	14.26	13.17	0.95	9.67	17.79	12.12	0.082	19.4	8.9	<0.001
Le Bricon-abbreviated MDRD	20.33	21.10	20.00	0.95	16.54	24.52	19.05	0.083	26.3	15.8	<0.001
Filler-abbreviated MDRD	22.03	22.73	22.06	0.98	17.85	27.38	20.02	0.073	28.0	17.5	0.002
Rule-MDRD	12.38	12.33	12.83	0.99	7.46	17.28	10.44	0.40	17.7	7.9	0.001
Larsson-MDRD	10.98	10.80	11.59	0.98	5.81	16.20	8.80	0.038	16.3	6.4	0.002
Hoek-MDRD	13.41	13.57	13.68	0.99	8.83	18.05	11.69	0.044	18.9	8.9	<0.001
Le Bricon-MDRD	20.27	20.41	20.50	0.99	15.69	24.77	18.62	0.044	25.7	15.8	<0.001
Filler-MDRD	21.96	22.04	22.56	0.99	17.00	27.64	19.59	0.043	27.4	17.5	0.004

Difference Between Creatinine-Based and Cystatin C-Based Formulas for GFR Estimation and Their Correlation with BMI, Age, and sex

The differences between GFRs estimated by cystatin C-based equations and those estimated by C-G and MDRD equations were greater in older patients (P value: 0.01 - 0.04).

The differences between GFRs estimated by cystatin C-based equations and creatinine-based equations were significantly different between males and females (P value: 0.15 - 0.001).

4. Discussion

Chronic kidney disease is an important public health problem. Estimation of GFR is essential for the evaluation of kidney function in CKD patients. The current kidney disease outcomes quality initiative (K/DOQI) guidelines classify CKD into five stages based on GFR estimations (10).

There is evidence showing that using creatinine concentration as an ideal marker for GFR estimation is accompanied by problems (22).

Studies have reported that cystatin C is less affected by age, gender, and muscle mass when compared to serum creatinine (23) and it is not affected also by dietary protein intake, inflammation, fever, and agents such as proteins and bilirubin (24).

Our aim in this study was to compare cystatin C-based equations with creatinine based-formulas for estimation of GFRs.

Many studied have suggested that cystatin C concentration is a better indicator to estimate GFR than serum creatinine concentration (9, 10, 25-30), especially in patients with spinal injury, liver cirrhosis, cystic fibrosis, diabetes, and old age (31). While, other investigators have reported that these two substances are equally accurate (14, 32-35).

Also, some researchers believe that many factors such as male sex, weight, height, cigarette smoking, higher serum C reactive protein levels, steroid therapy, and rheumatoid arthritis can increase the serum level of cystatin C. Thus, this substance may be less accurate to evaluate kidney function (35-38).

In this study, we calculated the GFRs of 120 patients with CKD based on creatinine and cystatin C equations. The results indicated that there was a significant correlation between all creatinine-based estimated GFRs and cystatin C-based estimated GFRs (P value < 0.001), and abbreviated MDRD-estimated GFRs were comparable with those of Hoek and Le Bricon equations in CKD subjects (P value < 0.001, r: 0.4, R2: 0.16).

In general, only the mean estimated GFR resulted from C-G formula was under the influence of BMI (P value < 0.001), because it was higher in individuals with higher BMI. Increasing age significantly reduced the mean estimated GFR (P value < 0.0001). This result was expected due to the influence of age and weight on C-G formula. But, we do not have any explanation why BMI and age were not effective in other creatinine-based equations (Table 5).

In addition, a relationship was verified between GFRs estimated by creatinine-based formulas and gender, but such a relation was not found in GFRs from cystatin C-based equations. Since the factors of weight, age, and gender are not considered in the cystatin C-based formulas, this result is not surprising.

On the other hand, since the number of patients on stages 2 and 5 CKD was low, we evaluated the effect of BMI, age, and sex on the prevalence of stages 3 - 4 CKD. The prevalence of stages 3 - 4 CKD, determined by C-G and MDRD formulas, was affected significantly by age (P value: 0.03 and 0.008, respectively).

Also, BMI had an influence on the prevalence of stages 3 - 4 CKD in creatinine-based formulas although it was not statistically significant. The effect of BMI was statistically significant only when C-G formula was used (P value: 0.005). Patients with higher BMI had lower frequency in stages 3 - 4 CKD.

Also, there were no significant sex differences in the prevalence of stages 3 - 4 CKD patients (P value > 0.05) by using creatinine-based formulas.

Differences in estimated GFRs between cystatin C-based equations and C-G and MDRD equations were greater in older patients (P value: 0.01 - 0.04, F: 3.2 - 4.1).

In terms of differences between GFRs estimated by cystatin C-based equations and GFRs estimated by creatinine-based formulas, they were lower at higher BMI levels when C-G equation was used (P value: 0.004 - 0.01), and they were greater in older patients when C-G and MDRD equations were used (P value: 0.01 - 0.04). The differences were also significant between males and females (P value: 0.15 - 0.001).

According to sex, all the creatinine-based formulas showed significant differences while cystatin C-based formulas did not. This result was predictable due to the influence of sex factor in creatinine-based equations, while sex factor is not considered in cystatin C-based equations.

4.1. To Summarize

Our findings revealed that the abbreviated MDRD formula, among creatinine-based GFR formulas, provides GFRs closer to GFRs estimated by cystatin C-based equations in CKD patients. Since the cost of laboratory tests for cystatin C is higher and it does not show superiority over MDRD, we recommend that the abbreviated MDRD formula be used for estimating GFR in CKD patients.

4.2. Limitation

There are two limitations for this study: 1) lack of a gold standard test and, 2) the small number of patients in the study.

Footnotes

References

1.
Rose BD. Clinical physiology of acid-base and electrolyte disorders. McGraw-Hill; 1977.
2.
Brochner-Mortensen J, Giese J, Rossing N. Renal inulin clearance versus total plasma clearance of 51Cr-EDTA. Scand J Clin Lab Invest. 1969;23(4):301-5. [PubMed ID: 4986443]. https://doi.org/10.3109/00365516909081695.
3.
Aurell M. Accurate and feasible measurements of GFR--is the iohexol clearance the answer? Nephrol Dial Transplant. 1994;9(9):1222-4. [PubMed ID: 7816278].
4.
Star R, Hostetter T, Hortin GL. New markers for kidney disease. Clin Chem. 2002;48(9):1375-6. [PubMed ID: 12194910].
5.
Levey AS, Coresh J, Balk E, Kausz AT, Levin A, Steffes MW, et al. National Kidney Foundation practice guidelines for chronic kidney disease: evaluation, classification, and stratification. Ann Intern Med. 2003;139(2):137-47. [PubMed ID: 12859163]. https://doi.org/10.7326/0003-4819-139-2-200307150-00013.
6.
Sjostrom PA, Odlind BG, Wolgast M. Extensive tubular secretion and reabsorption of creatinine in humans. Scand J Urol Nephrol. 1988;22(2):129-31. [PubMed ID: 3206217]. https://doi.org/10.1080/00365599.1988.11690398.
7.
Sandilands EA, Dhaun N, Dear JW, Webb DJ. Measurement of renal function in patients with chronic kidney disease. Br J Clin Pharmacol. 2013;76(4):504-15. [PubMed ID: 23802624]. https://doi.org/10.1111/bcp.12198.
8.
Maillard N, Mariat C, Bonneau C, Mehdi M, Thibaudin L, Laporte S, et al. Cystatin C-based equations in renal transplantation: moving toward a better glomerular filtration rate prediction? Transplantation. 2008;85(12):1855-8. [PubMed ID: 18580481]. https://doi.org/10.1097/TP.0b013e3181744225.
9.
Poge U, Gerhardt T, Stoffel-Wagner B, Palmedo H, Klehr HU, Sauerbruch T, et al. Prediction of glomerular filtration rate in renal transplant recipients: cystatin C or modification of diet in renal disease equation? Clin Transplant. 2006;20(2):200-5. [PubMed ID: 16640527]. https://doi.org/10.1111/j.1399-0012.2005.00466.x.
10.
Stevens LA, Coresh J, Greene T, Levey AS. Assessing kidney function--measured and estimated glomerular filtration rate. N Engl J Med. 2006;354(23):2473-83. [PubMed ID: 16760447]. https://doi.org/10.1056/NEJMra054415.
11.
Oddoze C, Morange S, Portugal H, Berland Y, Dussol B. Cystatin C is not more sensitive than creatinine for detecting early renal impairment in patients with diabetes. Am J Kidney Dis. 2001;38(2):310-6. [PubMed ID: 11479157]. https://doi.org/10.1053/ajkd.2001.26096.
12.
Le Bricon T, Thervet E, Froissart M, Benlakehal M, Bousquet B, Legendre C, et al. Plasma cystatin C is superior to 24-h creatinine clearance and plasma creatinine for estimation of glomerular filtration rate 3 months after kidney transplantation. Clin Chem. 2000;46(8 Pt 1):1206-7. [PubMed ID: 10926911].
13.
Filler G, Lepage N. Should the Schwartz formula for estimation of GFR be replaced by cystatin C formula? Pediatr Nephrol. 2003;18(10):981-5. [PubMed ID: 12920638]. https://doi.org/10.1007/s00467-003-1271-5.
14.
Hoek FJ, Kemperman FA, Krediet RT. A comparison between cystatin C, plasma creatinine and the Cockcroft and Gault formula for the estimation of glomerular filtration rate. Nephrol Dial Transplant. 2003;18(10):2024-31. [PubMed ID: 13679476]. https://doi.org/10.1093/ndt/gfg349.
15.
Larsson A, Malm J, Grubb A, Hansson LO. Calculation of glomerular filtration rate expressed in mL/min from plasma cystatin C values in mg/L. Scand J Clin Lab Invest. 2004;64(1):25-30. [PubMed ID: 15025426]. https://doi.org/10.1080/00365510410003723.
16.
Rule AD, Bergstralh EJ, Slezak JM, Bergert J, Larson TS. Glomerular filtration rate estimated by cystatin C among different clinical presentations. Kidney Int. 2006;69(2):399-405. [PubMed ID: 16408133]. https://doi.org/10.1038/sj.ki.5000073.
17.
Fried LF, Lee JS, Shlipak M, Chertow GM, Green C, Ding J, et al. Chronic kidney disease and functional limitation in older people: health, aging and body composition study. J Am Geriatr Soc. 2006;54(5):750-6. [PubMed ID: 16696739]. https://doi.org/10.1111/j.1532-5415.2006.00727.x.
18.
Muntner P, Winston J, Uribarri J, Mann D, Fox CS. Overweight, obesity, and elevated serum cystatin C levels in adults in the United States. Am J Med. 2008;121(4):341-8. [PubMed ID: 18374694]. https://doi.org/10.1016/j.amjmed.2008.01.003.
19.
Stevens L, Greene T, Li C. Factors other than GFR influencing serum cystatin. J Am Soc Nephrol. 2007;18:547-8.
20.
Kratchmarova I, Kalume DE, Blagoev B, Scherer PE, Podtelejnikov AV, Molina H, et al. A proteomic approach for identification of secreted proteins during the differentiation of 3T3-L1 preadipocytes to adipocytes. Mol Cell Proteomics. 2002;1(3):213-22. [PubMed ID: 12096121]. https://doi.org/10.1074/mcp.M200006-MCP200.
21.
Kopple JD. National kidney foundation K/DOQI clinical practice guidelines for nutrition in chronic renal failure. Am J Kidney Dis. 2001;37(1 Suppl 2):S66-70. [PubMed ID: 11158865]. https://doi.org/10.1053/ajkd.2001.20748.
22.
Grubb A. Non-invasive estimation of glomerular filtration rate (GFR). The Lund model: Simultaneous use of cystatin C- and creatinine-based GFR-prediction equations, clinical data and an internal quality check. Scand J Clin Lab Invest. 2010;70(2):65-70. [PubMed ID: 20170415]. https://doi.org/10.3109/00365511003642535.
23.
Baxmann AC, Ahmed MS, Marques NC, Menon VB, Pereira AB, Kirsztajn GM, et al. Influence of muscle mass and physical activity on serum and urinary creatinine and serum cystatin C. Clin J Am Soc Nephrol. 2008;3(2):348-54. [PubMed ID: 18235143]. https://doi.org/10.2215/CJN.02870707.
24.
Tangri N, Stevens LA, Schmid CH, Zhang YL, Beck GJ, Greene T, et al. Changes in dietary protein intake has no effect on serum cystatin C levels independent of the glomerular filtration rate. Kidney Int. 2011;79(4):471-7. [PubMed ID: 20980977]. https://doi.org/10.1038/ki.2010.431.
25.
Dharnidharka VR, Kwon C, Stevens G. Serum cystatin C is superior to serum creatinine as a marker of kidney function: a meta-analysis. Am J Kidney Dis. 2002;40(2):221-6. [PubMed ID: 12148093]. https://doi.org/10.1053/ajkd.2002.34487.
26.
Grubb A, Bjork J, Lindstrom V, Sterner G, Bondesson P, Nyman U. A cystatin C-based formula without anthropometric variables estimates glomerular filtration rate better than creatinine clearance using the Cockcroft-Gault formula. Scand J Clin Lab Invest. 2005;65(2):153-62. [PubMed ID: 16025838]. https://doi.org/10.1080/00365510510013596.
27.
Perkins BA, Nelson RG, Krolewski AS. Cystatin C and the risk of death. N Engl J Med. 2005;353(8):842-4. author reply 842-4. [PubMed ID: 16124125]. https://doi.org/10.1056/NEJMc051667.
28.
Gokkusu CA, Ozden TA, Gul H, Yildiz A. Relationship between plasma Cystatin C and creatinine in chronic renal diseases and Tx-transplant patients. Clin Biochem. 2004;37(2):94-7. [PubMed ID: 14725938].
29.
Thomassen SA, Johannesen IL, Erlandsen EJ, Abrahamsen J, Randers E. Serum cystatin C as a marker of the renal function in patients with spinal cord injury. Spinal Cord. 2002;40(10):524-8. [PubMed ID: 12235535]. https://doi.org/10.1038/sj.sc.3101320.
30.
Jenkins MA, Brown DJ, Ierino FL, Ratnaike SI. Cystatin C for estimation of glomerular filtration rate in patients with spinal cord injury. Ann Clin Biochem. 2003;40(Pt 4):364-8. [PubMed ID: 12880536]. https://doi.org/10.1258/000456303766476995.
31.
Beringer PM, Hidayat L, Heed A, Zheng L, Owens H, Benitez D, et al. GFR estimates using cystatin C are superior to serum creatinine in adult patients with cystic fibrosis. J Cyst Fibros. 2009;8(1):19-25. [PubMed ID: 18799365]. https://doi.org/10.1016/j.jcf.2008.07.004.
32.
Momtaz HE, Dehghan A, Karimian M. Correlation of cystatin C and creatinine based estimates of renal function in children with hydronephrosis. J Renal Inj Prev. 2016;5(1):25-8. [PubMed ID: 27069964]. https://doi.org/10.15171/jrip.2016.06.
33.
Stevens LA, Coresh J, Schmid CH, Feldman HI, Froissart M, Kusek J, et al. Estimating GFR using serum cystatin C alone and in combination with serum creatinine: a pooled analysis of 3,418 individuals with CKD. Am J Kidney Dis. 2008;51(3):395-406. [PubMed ID: 18295055]. https://doi.org/10.1053/j.ajkd.2007.11.018.
34.
Cepeda FJ, Fernandez E, Pobes A, Banos LM. [Utility of cystatin-C in hospitalized patients. Comparing with different methods of assessing renal function]. Nefrologia. 2007;27(2):168-74. [PubMed ID: 17564561].
35.
Donadio C, Lucchesi A, Ardini M, Giordani R. Cystatin C, beta 2-microglobulin, and retinol-binding protein as indicators of glomerular filtration rate: comparison with plasma creatinine. J Pharm Biomed Anal. 2001;24(5-6):835-42. [PubMed ID: 11248475]. https://doi.org/10.1016/S0731-7085(00)00550-1.
36.
Knight EL, Verhave JC, Spiegelman D, Hillege HL, de Zeeuw D, Curhan GC, et al. Factors influencing serum cystatin C levels other than renal function and the impact on renal function measurement. Kidney Int. 2004;65(4):1416-21. [PubMed ID: 15086483]. https://doi.org/10.1111/j.1523-1755.2004.00517.x.
37.
Wasen E, Isoaho R, Mattila K, Vahlberg T, Kivela SL, Irjala K. Serum cystatin C in the aged: relationships with health status. Am J Kidney Dis. 2003;42(1):36-43. [PubMed ID: 12830454]. https://doi.org/10.1016/S0272-6386(03)00406-2.
38.
Uzun H, Ozmen Keles M, Ataman R, Aydin S, Kalender B, Uslu E, et al. Serum cystatin C level as a potentially good marker for impaired kidney function. Clin Biochem. 2005;38(9):792-8. [PubMed ID: 16005452]. https://doi.org/10.1016/j.clinbiochem.2005.05.012.

comments

Crossmark

Checking

Share on

Comments

Number of Comments:0

Cited by

Metrics

Get Permission (article level)

Purchasing Reprints

Copyright Clearance Center (CCC) handles bulk orders for article reprints for Brieflands. To place an order for reprints, please click here ( https://www.copyright.com/landing/reprintsinquiryform/ ). Clicking this link will bring you to a CCC request form where you can provide the details of your order. Once complete, please click the ‘Submit Request’ button and CCC’s Reprints Services team will generate a quote for your review.

Search Relations

Author(s):

Nouraddin Mousavinasab:[PubMed][Scholar]
Mojgan Jalalzadeh:[PubMed][Scholar]