Abstract
Keywords
Photon-Therapy Radio-Sensitized Tumor Nanoparticles Monte Carlo Simulation
1. Background
Radiation therapy or radiotherapy is one of the most common treatments for cancer. It deals with treatment using high-energy particles or waves. Radiotherapy is one of the most important branches of medical radiation physics, which deals with beams of ions. In this method, due to the damage to DNA, treatment area cells (target tissue) are destroyed and their growth and division will be impossible. One of the problems with this method is the recurrence of the disease. The most important cause of the recurrence is that the absorbed energy (dose) in normal tissue is similar to the absorbed dose of the tumor; in other words, the efficiency is low. This leads to a lack of necrosis dose transmission to the tumor, causing the recurrence (1). Therefore, finding a method to improve the absorbed dose in the tumor and carry out the treatment more efficiently is a big step towards solving this problem. To achieve this goal, several methods, such as BNCT (boron neutron capture therapy), SRS (stereotactic radiosurgery), and IMRT (intensity-modulated radiation therapy) are employed to maximize the dose delivered locally to the tumor (2-4). Special attention is recently paid to nanotechnology and nanoparticles are studied more extensively; leading to experiment this field in cancer treatment in the form of nanomedicine and nanobiology. In this new therapeutic approach, to increase the dose absorbed by tumor cells compared to the absorbed dose in healthy cells, a chemical compound consisting of nanoparticles is used to sensitize the tumor cells.
Intense activity of cancer cells and wider capillaries of the tumor relative to normal tissue cause the intended compounds, which have larger molecules than the nutrients in the blood vessels, be absorbed more in the tumor. At this point, it is said that the tumor is “sensitized” by nanoparticles. The tumor is, then, irradiated with the monochromatic X-ray beam. Due to the high interaction cross-section of nanoparticles, significant interactions happen between nanoparticles and radiation and as a result, a large number of electrons are produced. The electrons, as the ionizing radiation, cause an increase in the local dose.
Benefits and applications of this treatment method are shown in various research activities by experimental treatment of animal tumors and by in vitro irradiation of human cells (5-10). Therefore, dose enhancement calculations in a typical tumor sensitized by nanoparticles are required for a precise evaluation of this treatment method. For clinical application, factors affecting that treatment technique should be carefully and quantitatively evaluated. Few research activities are performed for a quantitative evaluation of dose enhancement and the factors influencing this treatment method. Since conducting an experiment on a real tumor creates its own problems and is expensive, an evaluation of this therapeutic approach using experimental tests is not economical. For the intended calculations, using a numerical method that can simulate particle transport is an efficient choice. The Monte Carlo method is the most promising scheme for (11) tracking particles in the material and quantitative evaluation of its influences. Homogenous and nonhomogeneous distributions of nanoparticles are usually 2 important approaches adopted for a macroscopic simulation of a nanoparticle aided tumor irradiation using the Monte Carlo method (11-15).
Mousavie et al. simulated a semi-random distribution of gold nanoparticles (GNP) in a Plexiglas phantom to evaluate the dose enhancement (12). Mesbahi et al. (11) modeled a 20 × 20 × 20 cm3 water phantom containing a 1 × 1 × 1 cm3 gold nanoparticle-aided tumor located at 2 different depths, 2 cm for megavoltage photon beams and at surface for kilovoltage photon beams. They assessed the influence of nanoparticle size, concentration, and photon energy on dose enhancement. They demonstrated that no significant dose enhancement can be achieved by megavoltage photon beams, however, the dose enhances significantly for kilovoltage photon beams. The photoelectric and Compton interactions are the dominant interaction modes in low and high energies, respectively. Therefore, the photoelectric interaction is the responsible interaction for dose enhancement. Ranjbar et al. evaluated the dose enhancement factor in the gold nanoparticle-aided tumor. In their study, the gold nanoparticles were supposed to be distributed homogenously in the tumor located in a brain phantom with simplified material compositions (15). They concluded that nanoparticle concentration, photon beam energy, and tumor depth were the influential factors in this treatment method. Also, some research studies are conducted to obtain the effect of quantitative nanoparticles in the nano dimension (16). Paro et al. compared 2 calculation methods as analytical and Monte Carlo methods to evaluate the nanoparticle type, concentration, and photon energy. They simulated a single nanoparticle located at the center of a cell modeled as a slab of tissue (17). They concluded that a peak appeared in dose enhancement factor when the energy increased, which demonstrated the optimum energy.
The investigations conducted in this field focused on the influence of the presence of a nanoparticle in an environment similar to a cell. To the best of the authors` knowledge, the influence of potential influential factors using a real brain and tumor was not investigated in the literature. Such an investigation is crucial to assess the efficiency of such treatment strategies in clinical applications. Also, in most of the studies, only gold nanoparticles were assessed. Recently, the benefits and applications of gold, silver, and platinum nanoparticles in nanoparticle-aided photon therapy are realized, and the corresponding safety tests are also performed for clinical use. Therefore, the current study aimed at investigating the factors affecting this treatment method regarding the 3 types of nanoparticles. To that end, a cubic phantom of the brain with real tissue and materials was modeled using the Monte Carlo method to obtain more accurate quantitative influence of the presence of nanoparticles in a typical tumor.
The predominant interaction mode in the sensitized tumor was photoelectric due to the high atomic number of sensitizing elements; in addition, the X-ray energy was in the range of K-edge energy in the photon therapy. Photoelectric attenuation strongly depends on the atomic number of the elements. Therefore, the type of nanoparticles influences the dose enhancement. On the other hand, when a beam of mono-energetic X-ray passes through a greater concentration of an element, the radiation intensity decreases more, which represent an increase in the incident of photon interaction. Therefore, the nanoparticle concentration is another influential factor in this method. In the photoelectric cross-section curve, there is a lack of uniformity called absorption edge. Attenuation probability increases rapidly in this energy by a factor of 10, which in turn enhances interaction and increases the dose. Therefore, energy can be the next influential factor. Finally, it is clear that the photon flux steadily decreases with increasing the depth; therefore, the electron production and consequently the dose are reduced. As a result, the depth is the 4th influential factor in this treatment approach. Therefore, in the current study, the type and concentration of nanoparticles, photon energy, and depth of tumor were assessed as potentially influential factors.
2. Methods
The current study employed MCNPX Code version 2.4 (Los Alamos National Laboratory, United States). In the simulations for protons, neutrons, and photons the LA150H, the LA150N, and the MCPLIB04 libraries were used, respectively. For the particles and energy, for which information was not available in the library, physical models were implemented in the code. MCNPX code can simulate almost all the particles at all energies and accurately calculates the dose and flux (18). Therefore, despite the development of newer codes, this code is used to assess methods of radiation therapy. The mathematical basis of MCNPX code is developed through the Monte Carlo method, which is a statistical approach. One application of the Monte Carlo method is replication. To that end, a statistical model is developed similar to what happens in reality, using the random numbers and random motion of particles, and is repeated several times (19). Therefore, the Monte Carlo simulation method can be considered as a thought experiment.
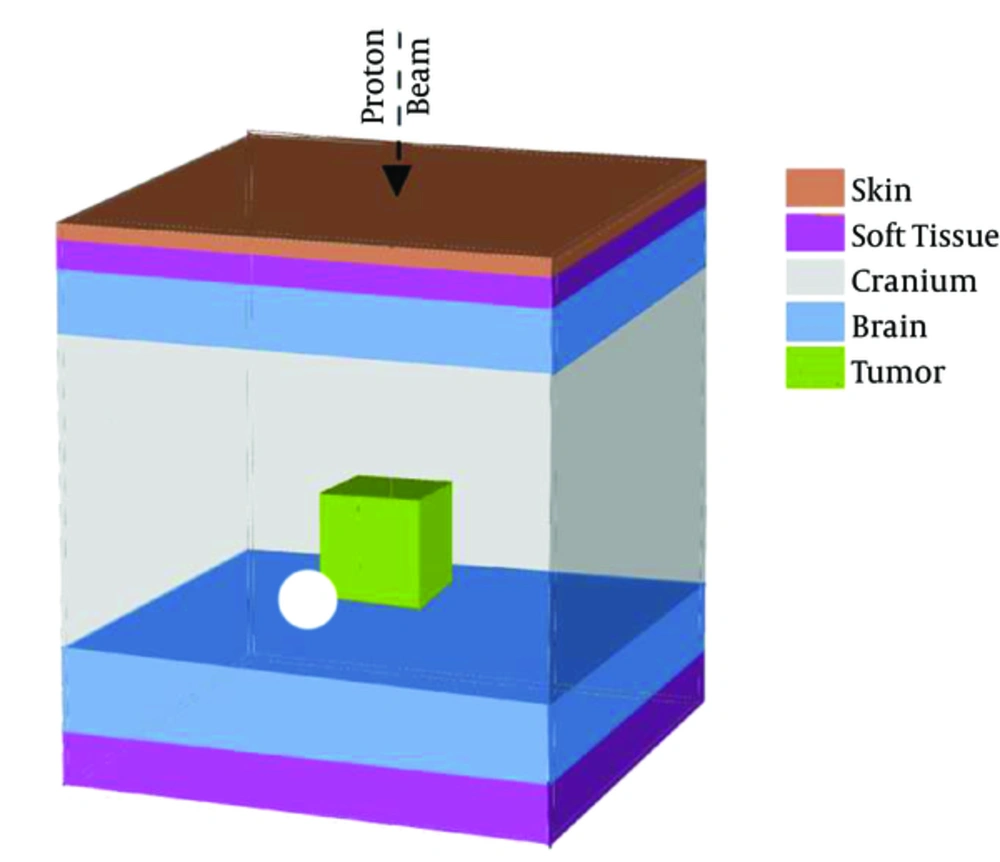
The overall geometry for the head phantom used in the current study, as presented in Figure 1, was a layered cube with the following specifications: 0.2 cm human skin, 0.3 cm soft tissue, 0.9 cm cranium, 11.5 cm brain, 0.9 cm cranium, and finally, 0.5 cm soft tissue. Here, the lateral dimensions of the phantom were considered in accordance with the maximum values of the brain in the MIRD-ORNL phantom as 17.2 × 13.2 cm (20). A 2-cm tumor was considered within the depth of 7 cm. The kind and elemental composition of the tissue in the head phantom are expressed as percentage in Table 1 (21), and tumor specifications with the homogenized nanoparticle agents with different concentrations of 10, 25, 50, and 75 mg nanoparticles per mL of tumor material are presented in Table 1.
Geometry of the Slab Head Phantom
Mass Density and Elemental Composition of the Tissue in the Head Phantom for Sensitized and Non-sensitized Tumors
| Tissue Type | Density, g/cm3 | H | C | N | O | Ca | Na | P | S | Cl | K | Au |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Skin | 1.09 | 10.0 | 20.4 | 4.2 | 64.5 | - | 0.2 | 0.1 | 0.2 | 0.3 | 0.1 | - |
| Soft tissue | 1.03 | 10.5 | 25.6 | 2.7 | 60.2 | - | 0.1 | 0.2 | 0.3 | 0.2 | 0.2 | - |
| Skull bone | 1.61 | 5.0 | 21.2 | 4.0 | 43.5 | 17.6 | 0.1 | 8.1 | 0.3 | - | - | - |
| Brain | 1.04 | 10.7 | 14.5 | 2.2 | 71.2 | - | 0.2 | 0.4 | 0.2 | 0.3 | 0.3 | - |
| Non-sensitized tumor | 1.04 | 10.7 | 14.5 | 2.2 | 71.2 | - | 0.2 | 0.4 | 0.2 | 0.3 | 0.3 | - |
| Sensitized Tumor Containing Different Concentration of GNPs | ||||||||||||
| 10 mg Au mL-1 | 1.05 | 10.6 | 14.4 | 2.2 | 70.5 | - | 0.2 | 0.4 | 0.2 | 0.3 | 0.3 | 1.0 |
| 25 mg Au mL-1 | 1.07 | 10.4 | 14.2 | 2.1 | 69.5 | - | 0.2 | 0.4 | 0.2 | 0.3 | 0.3 | 2.3 |
| 50 mg Au mL-1 | 1.09 | 10.2 | 13.8 | 2.1 | 67.9 | - | 0.2 | 0.4 | 0.2 | 0.3 | 0.3 | 4.6 |
| 75 mg NP mL-1 | 1.12 | 10.0 | 13.5 | 2.1 | 66.4 | - | 0.2 | 0.4 | 0.2 | 0.3 | 0.3 | 6.7 |
It does not seem very appropriate to use X-ray photons emitted from the lamp generator in this method as the interfacial doses (ie, skin surface dose) and the tissue located at the radiation path, before the tumor, increase due to the existence of low-energy photons in the spectrum. On the other hand, if filtration is used to remove these photons, the flux is substantially reduced. In this case, to achieve the prescribed dose, the exposure time should be increased, which is not desirable in terms of the treatment. To overcome this problem, the use of monochromatic radiation of the synchrotron is recommended due to the following advantages: 1) The ability to produce monochromatic radiation with high flux; 2) The ability to create parallel beams with minimal divergence on the route and the lowest halftone in the tissue; 3) The possibility of producing polarized X-ray beams with minimal dispersion in the unwanted routes and protecting the sensitive organs nearby. Therefore, in the current study, monochromatic beams were employed. To calculate photon therapy, a 2 × 2 cm2 surface source was considered with a source-surface distance (SSD) of 50 cm. The photon beam was vertically irradiated on the surface of the phantom. Several energies for irradiated photon, near to the K-edge energy of each particle, were investigated.
1. For gold (K-edge energy = 80.73 keV): 75, 85, 95, 105 keV
2. For platinum (K-edge energy = 78.40): 75, 85, 95, 105 keV
3. For silver (K-edge energy = 25.53 keV): 35, 45, 55, 65 keV
To achieve maximum precision, the energy considered here was an equivalent of the least amount of cutoff energy that can be traced by MCNPX Code; ie, 1 keV for photon and electron and 1 MeV for neutron and proton; 3,500,000 photons were traced to achieve a relative error of less than 0.01.
Following card was used to obtain energy deposition per unit volume (MeV/cm3/particle):
RMESH: P pedep
Finally, dose (nGy/particle) was calculated by the following equation:
3. Results
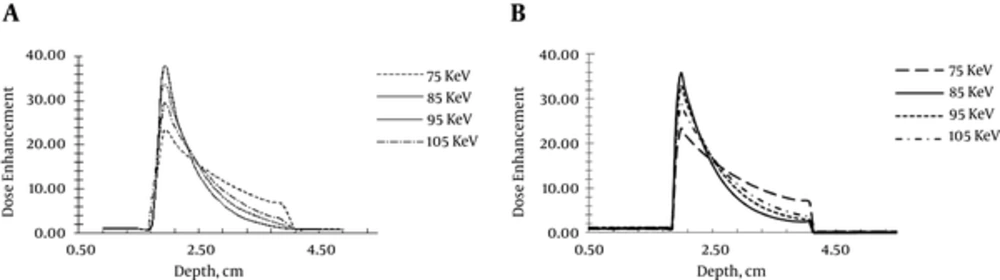
To develop a correct model, at the first step of the current study, a model was developed according to the study conducted by Ranjbar et al. (15). In that study, the brain phantom containing a number of important compounds was modeled and the other tissue of the human head was not considered. A gold nanoparticle sensitized tumor was modeled and the impacts of various factors on the radiation dose enhancement in the tumor were studied. The dose enhancement factor distribution obtained by this model developed in the current study and the results reported by Ranjbar et al. (15) are shown in Figure 2. Dose enhancement factor distribution of different photon energies is presented in Figure 2. Dose enhancement profiles corresponding to different photon energies obtained in the current study were in good agreement with those of Ranjbar et al. (15). Therefore, it can be concluded that the developed model in the current study was valid and can be used for further development, based on the current study goals.
The Dose Enhancement Factor Distribution Reported by A, Ranjbar et al. and B, the Results Obtained by the Early Model Developed in the Current Study
At the next step of the current study, an accurate model was developed based on the head phantom described in section 2. The current study obtained the following results:
3.1. Influence of Photon Energy
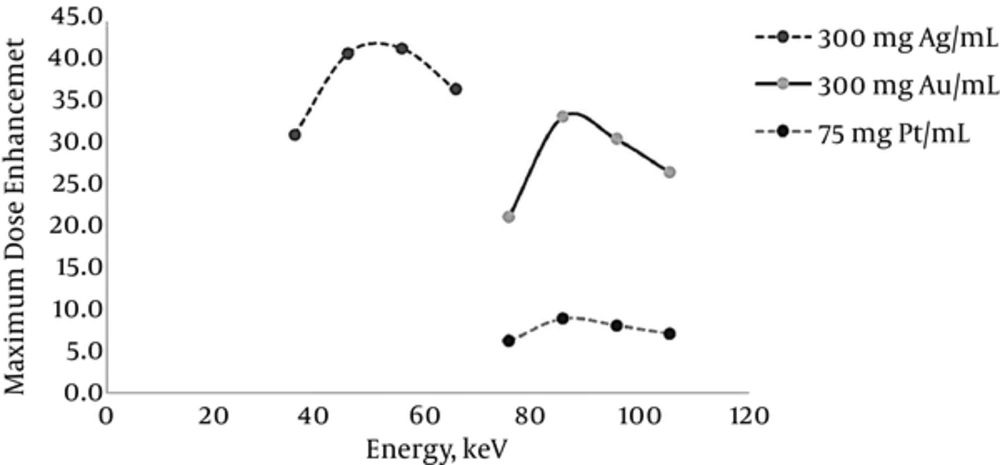
According to the attenuation coefficient reduction, by increasing photon energy and also due to the lack of uniformity in the curve of photon attenuation, an optimum energy should be found. To obtain optimum energy corresponding to silver, gold, and platinum as the sensitizer agents in the sensitized tumor, the X-ray beams with energies near to K-edge energy of nanoparticles under study were used. The maximum dose enhancement corresponding to the elements under study is shown in Figure 3. The optimum energy for gold and platinum was 85 to 95 keV, which was near to those elements K-edge energy (80.73 keV for gold and 78.40 keV for platinum). Due to the photons attenuation before entering the tumor, the photon energy decreased. Note that the incident photon energy should be greater than that of the K-edge energy to compensate the energy loss due to the attenuation. The attenuation is more significant when the photon energy is low. That is why, for example, the optimal energy for silver (35 to 45 keV) is almost 10 to 20 keV more than that of the silver K-edge energy (25.53 keV).
The Maximum Dose Enhancement
3.2. Influence of Nanoparticle Type
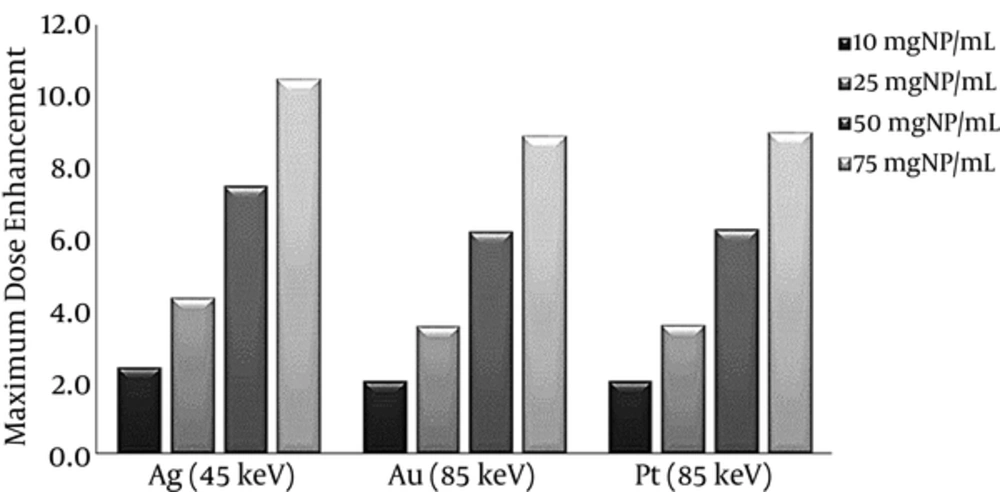
To evaluate the effects of the sensitizer agent type on dose enhancement in the tumor, gold, silver, and platinum nanoparticles were studied. In the current simulation, the monochromatic photons with energies around optimum were applied and the nanoparticle concentration was intended to be 50 mgNP/mL. To obtain the dose enhancement, due to the presence of gold and platinum nanoparticles, X-rays with energies of 75, 85, 95, and 105 keV were used. In the case of silver nanoparticles, the X-rays with energies of 35, 45, 55, and 65 keV were applied. It can be concluded from the dose enhancement curve (Figure 4) that first, the dose in the sensitized tumor always increases dramatically due to the presence of nanoparticles. The steepest curve corresponds to the optimum energy, which represents a difference of 5.8 between the maximum and minimum. Second, due to the maximum attenuation coefficient of photons at K-edge energy, the maximum dose enhancement is achieved in the optimal energy corresponding to the element. Maximum dose enhancement achieved in gold and platinum-sensitized tumor was 6.2, which corresponded to the photon energy of 85 keV. For silver, this value was 7.5, which corresponded to the photon energy of 45 keV. Third, the dose enhancement factor decreases by an increase in depth, as the photon energy drops below the photoelectric interaction region. Finally, the dose enhancement factor of the tumor surrounding normal tissue is 0.4 to 0.7, which demonstrates the dose reduction in the tumor surrounding normal tissue and, therefore, decrease in the potential damages to the healthy tissue.
The Dose Enhancement in the Tumor Sensitized by A, Gold; B Platinum; C, Silver with a Concentration of 50 mgNP/mL.
Based on Figure 5, in all concentrations the dose enhancement factor corresponding to the tumor sensitized by silver nanoparticles had the highest value (10.5 for 75 mgAg/mL); therefore, this element can be considered as the most effective agent to enhance the dose.
The Dose Enhancement in the Tumor Sensitized by Gold, Platinum, and Silver with a Concentration of 50 mgNP/mL at Optimum Energy.
3.3. Influence of Concentration
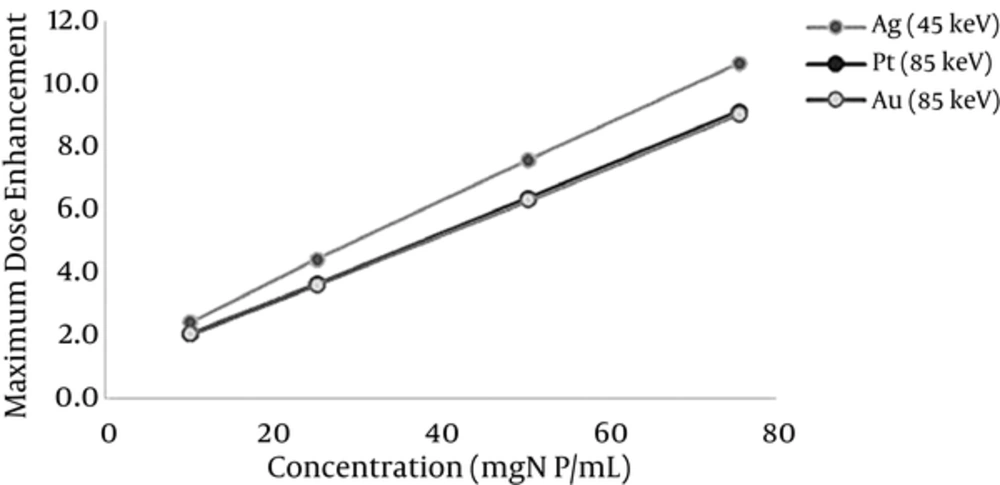
To assess the impact of nanoparticle concentration on dose enhancement, several simulations were conducted for different concentrations of nanoparticles including 10, 25, 50, and 75 mgNP/mL. The X-ray with an optimum energy corresponding to the elements under study was considered. Figure 6 illustrates that the dose enhancement factor increased according to increasing changes following a linear function with a solidarity coefficient of 0.99.
The Calculated Dose Enhancement for Different Concentrations of Gold, Platinum, and Silver, at Corresponding Optimal Energies
3.4. Influence of Tumor Depth
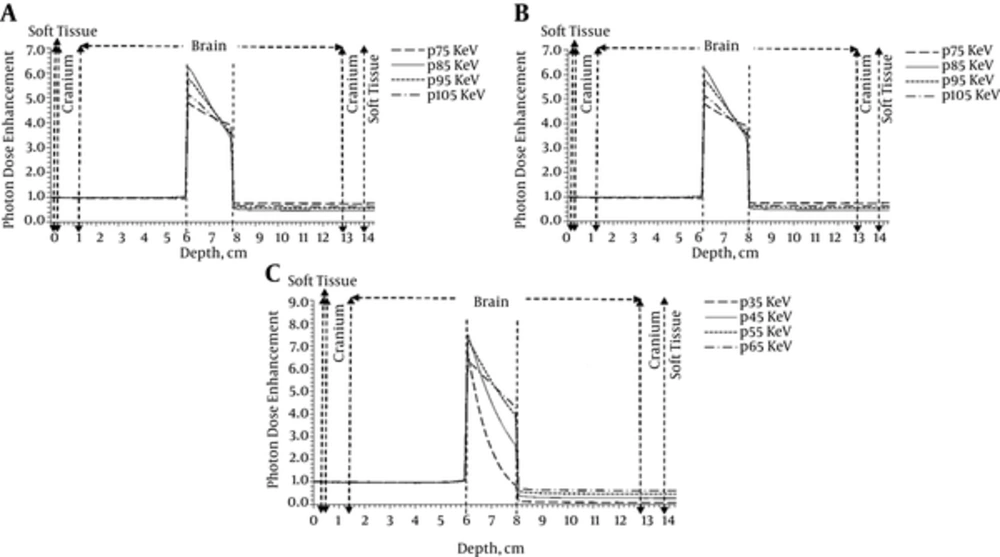
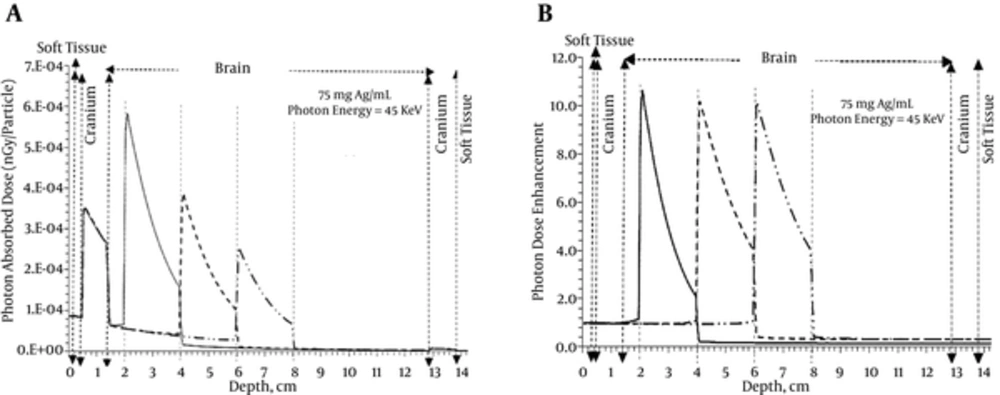
This therapeutic method is used to treat other tumors in different depths of 3, 5, and 7 cm. At this stage, the silver nanoparticles of 75 mgAg/mL and the X-ray of 45 keV, as optimal energy for silver, were used. Figure 7 shows the depth dose enhancement along the central axis when the tumor was in 3 different depths. The dose enhancement decreased with increasing depth from 10.5 to 10.0 cm. It means, as expected, the radiosensitization was more effective for more superficial tumors.
Dose, (A) Dose Enhancement (B) for 45 keV X-ray and Tumors Located at Different Depths
4. Discussion
Paro et al. (17) assessed dose enhancement in the presence of gold, silver, bismuth, and copper nanoparticles. Based on their assessments, gold was the most promising nanoparticle due to its high dose enhancement factor. Their experiment was performed using a Plexiglas phantom, which does not reflect the real material composition of the brain. Based on the accurate simulation conducted in the current study, silver was the most promising nanoparticle with a slightly bigger dose enhancement.
Mousavie Anijdan et al. (12) concluded that photoelectric interaction depends on atomic number and its cross-section shows several peaks at K- and L-edge energies. As a result, one can expect optimum energy corresponding to the nanoparticle used as sensitizing agent. Based on the figures presented by Paro et al. (17), the optimum energy was about 70 keV and 40 keV for gold and silver nanoparticles, respectively. Ranjbar et al. (15) reported that the optimum energy for gold nanoparticles ranged between 83 and 90 keV. These results were in good agreement with those obtained in the current study.
The results of Mousavie Anijdan et al. (12) showed that dose enhancement was directly proportionate to the gold nanoparticle concentration, while the effect of gold nanoparticle size was not significant. The results of the study by Paro et al. (17) showed that the dose enhancement factor increased by concentration. Ranjbar et al. (15) demonstrated the linear dependency of the dose enhancement factor on nanoparticle concentration. The same dependency between dose enhancement and concentration was obtained in the current study.
Ranjbar et al. suspected that the tumor dose might be less than skin dose after a certain depth
(15). It should be noted that they did not model all human head tissue. As can be observed in the depth-dose obtained in the current study, the tumor dose was less than cranium dose after a certain depth. In other words, although in the high depth, the dose enhancement factor was significant, the cranium absorbed dose was more than tumor dose. This effect was not observed in the soft tissue and skin. To overcome this problem, the multidirectional beam used in conventional radiotherapy can be applied.
4.1. Conclusion
In the current study, dose enhancement for several nanoparticle radiosensitizers was assessed in photon therapy. A slice of human head phantom containing real material composition of tissue in the head was simulated by MCNPX code, version 2.4. The type, concentration of the nanoparticles, and energy of the photon were studied as influential factors. In the case of silver nanoparticles, the optimum energy to achieve maximum dose enhancement ranged between 35 and 45 keV, which was 10 to 20 keV more than the corresponding K-edge energy. Optimum energy for gold and platinum was 85 to 95 keV, which was near to the K-edge energy of these elements.
A peak appeared in dose enhancement factor when the energy increased, demonstrating the optimum energy. Based on the figures presented in the article, the optimum energy was around 70 keV and 40 keV for gold and silver nanoparticles, respectively. The dose enhancement in the presence of gold, silver, bismuth, and copper nanoparticles was assessed. Based on the assessments, silver was the most promising nanoparticle due to its high dose enhancement factor.
To calculate the dose in the tumor and the effect of nanoparticle type on dose enhancement, 3 nanoparticles including gold, silver, and platinum were evaluated. In this part of the simulation, the X-rays with energy near to the K-edge energy of each element were used. In the case of silver nanoparticles, a higher range of energy was considered to compensate for the higher attenuation of photons in lower energies. In terms of dose enhancement, as the current study showed, silver nanoparticles were the best option. Finally, it was concluded that dose enhancement increased linearly with increasing the nanoparticle concentration. The sensitizer element addition caused a steep decrease in the radiation dose of the tumor due to the self-absorption that occurred in the area containing sensitizer elements. Finally, the dose enhancement decreased with increasing the depth due to the decrease in photons.
References
-
1.
Cameron JR, Skofronick JG. Medical Physics. Wiley Online Library; 1978.
-
2.
Barth RF, Soloway AH, Fairchild RG, Brugger RM. Boron neutron capture therapy for cancer. Realities and prospects. Cancer. 1992;70(12):2995-3007. [PubMed ID: 1451084].
-
3.
Phillips MH, Stelzer KJ, Griffin TW, Mayberg MR, Winn HR. Stereotactic radiosurgery: a review and comparison of methods. J Clin Oncol. 1994;12(5):1085-99. [PubMed ID: 8164033]. https://doi.org/10.1200/JCO.1994.12.5.1085.
-
4.
Webb S. Evaluation of Dose Enhancement in Radio Sensi. Philadelphia: Institute of Physics Publishing; 2001.
-
5.
Navabpour N, Mofid M. Introducing a new system for cancer tumor treatment. 2004.
-
6.
Rahman WN, Bishara N, Ackerly T, He CF, Jackson P, Wong C, et al. Enhancement of radiation effects by gold nanoparticles for superficial radiation therapy. Nanomed Nanotechnol Biol Med. 2009;5(2):136-42.
-
7.
Corde S, Joubert A, Adam JF, Charvet AM, Le Bas JF, Esteve F, et al. Synchrotron radiation-based experimental determination of the optimal energy for cell radiotoxicity enhancement following photoelectric effect on stable iodinated compounds. Br J Cancer. 2004;91(3):544-51. [PubMed ID: 15266326]. https://doi.org/10.1038/sj.bjc.6601951.
-
8.
Herold DM, Das IJ, Stobbe CC, Iyer RV, Chapman JD. Gold microspheres: a selective technique for producing biologically effective dose enhancement. Int J Radiat Biol. 2000;76(10):1357-64. [PubMed ID: 11057744].
-
9.
Hainfeld JF, Slatkin DN, Focella TM, Smilowitz HM. Gold nanoparticles: a new X-ray contrast agent. Br J Radiol. 2006;79(939):248-53. [PubMed ID: 16498039]. https://doi.org/10.1259/bjr/13169882.
-
10.
Navabpour M, Mofid B, Nazari MH. Study the photoelectron therapy effects on human cancer cells. J Lor Uni Med Sci. 2006;8:79-84.
-
11.
Mesbahi A, Jamali F, Garehaghaji N. Effect of photon beam energy, gold nanoparticle size and concentration on the dose enhancement in radiation therapy. Bioimpacts. 2013;3(1):29-35. [PubMed ID: 23678467]. https://doi.org/10.5681/bi.2013.002.
-
12.
Mousavie Anijdan SH, Shirazi A, Mahdavi SR, Ezzati A, Mofid B, Khoei S, et al. Megavoltage dose enhancement of gold nanoparticles for different geometric set-ups: Measurements and Monte Carlo simulation. Iran J Radiat Res. 2012;10(3):183-6.
-
13.
Ezzati AO, Mahdavi SR, Anijdan HM. Size Effects of Gold and Iron Nanoparticles on Radiation Dose Enhancement in Brachytherapy and Teletherapy: A Monte Carlo Study. Iran J Med Phys. 2014;11:253-9.
-
14.
Khosravi H, Mahdavi A, Rahmani F, Ebadi A. The Impact of Nano-Sized Gold Particles on the Target Dose Enhancement Based on Photon Beams Using by Monte Carlo Method. Nanomed Res J. 2016;1(2):84-9.
-
15.
Ranjbar H, Shamsaei M, Ghasemi MR. Investigation of the dose enhancement factor of high intensity low mono-energetic X-ray radiation with labeled tissues by gold nanoparticles. Nukleonika. 2010;55:307-12.
-
16.
Lin Y, McMahon SJ, Scarpelli M, Paganetti H, Schuemann J. Comparing gold nano-particle enhanced radiotherapy with protons, megavoltage photons and kilovoltage photons: a Monte Carlo simulation. Phys Med Biol. 2014;59(24):7675.
-
17.
Paro AD, Hossain M, Webster TJ, Su M. Monte Carlo and analytic simulations in nanoparticle-enhanced radiation therapy. Int J Nanomedicine. 2016;11:4735-41. [PubMed ID: 27695329]. https://doi.org/10.2147/IJN.S114025.
-
18.
Waters LS. MCNPX user’s manual, version 2.4. 0. Los Alamos: Los Alamos National Laboratory; 2002.
-
19.
Hendricks JS, Adam KJ, Booth TE, Briesmeister JF, Carter LL, Cox LJ, et al. Present and future capabilities of MCNP. Appl Radiat Isot. 2000;53(4-5):857-61. [PubMed ID: 11003531].
-
20.
Eckerman KF, Cristy M, Ryman JC. The ORNL mathematical phantom series. Oak Ridge: Oak Ridge National Laboratory; 2006.
-
21.
Wambersie A, Zoetelief J, Menzel HG, Paretzke H. The ICRU (International Commission on Radiation Units and Measurements): its contribution to dosimetry in diagnostic and interventional radiology. Radiat Protect Dosimetry. 2005;117(1-3):7-12.