1. Background
In intensity modulated radiotherapy (IMRT), photon beams produced by a medical linear accelerator (LINAC) are used to irradiate a cancer tumour. The aim of the radiation dose delivery is to achieve adequate dose coverage at the target, while sparing the surrounding health tissues. IMRT can significantly improve the outcome of radiotherapy and is being used to treat many different cancer sites such as brain, head-and-neck, lung, breast, and prostate effectively (1). Since IMRT usually uses the multileaf collimator (MLC) to produce beam intensity modulation in dose delivery, developing an efficient and precise leaf sequencing algorithm becomes essential. MLC is a computer-controlled collimator consists of a set of leaf pairs in opposition direction with the same sizes. The collimator is an intensity modulator converting a given beam profile into a modulated profile or intensity map needed in the treatment.
In IMRT, beam intensity modulation can be achieved by two approaches namely, the static and dynamic MLC (2). The static MLC approach is realized by sequentially delivering sequences of beam segments (shapes). When the leaves move from the setting position for one segment to another position for the next segment, the beam is switched off. The LINAC console then verifies if the MLC leaves are correctly at the new setting positions to switch the beam on again (step-and-shoot). There are many advantages of the static MLC approach such as easy verification, precise dose delivery, and general availability (2). The disadvantages of static MLC include lower delivered dose resolution and overshoot effect (3). In dynamic MLC approach, however, the beam is always on, and the intensity modulation is realized by adjusting the speed of the moving leaves. The advantage of the dynamic technique is its delivery efficiency, but more monitor unit is generally required because beam is on during the radiation delivery (4). Ma et al. (5) developed an algorithm, which could optimize the total monitor unit for a MLC based on algebraic expression for the area under the beam profile. However, according to Xia and Verhey’s analysis, the static MLC approach is superior to the dynamic MLC in IMRT (6). Therefore, only the static MLC approach is focused on in this study.
The MLC consists of heavy-metal (tungsten) leaves which can block the megavoltage radiation beams. For each row of the intensity matrix/profile, there is a pair of leaves associated: the left leaf and right leaf that can be moved in the direction of row. For the required intensity maps generated from an inverse treatment planning system, leaf sequencing is carried out to produce the corresponding intensity map using the MLC. After discretizing the irradiated area into bixels, an intensity function can be considered as an m × n matrix A with nonnegative integer entries, where entry ai,j indicates the desired intensity at bixel (i, j). From works of Galvin et al. and Bortfeld et al. (7, 8), several algorithms have been developed. The Bortfeld-Boyer algorithm provided the smallest possible total number of monitor unit (TNMU) but a large number of segment (NS). There are other algorithms aiming at reducing the NS at the price of an increased TNMU (9). Still, the leaf sequencing can be formulated as an integer programming problem, but the efficiency of MLC movement can further be improved.
2. Objectives
In this study, we proposed a new leaf sequencing algorithm for IMRT. Our algorithm can maximize the radiation delivery efficiency, reduce patient treatment time (reduced monitor unit), increase patient throughput and reduce the maintenance cost of the LINAC.
3. Methods
Our leaf sequencing algorithm employed Xia’s method (10) to initiate the input beam intensity map based on the model of Langer et al. (11). The total leaf travel distance (LTD) is used as a key constraint from our model in intensity modulation.
3.1. Intensity Modulation Model
The photon beam intensity modulation can be modelled as a mathematical problem by considering to decompose a given m × n integer matrix into a positive linear combination of (0, 1) matrices with the strict consecutive 1’s property in rows. The integer matrix can be expressed as (Equation 1):

Where A is the intensity matrix of m row and n column. Si is the corresponding (0, 1) matrices with the strict consecutive 1’s. ui is the LINAC beam monitor unit in each MLC aperture. The mathematical problem is to reduce an intensity matrix A(i, j) into a group of MLC beam segments which fields can be generated by a MLC. Matrix elements in A(i, j) are assumed to be nonnegative integers representing the photon beam intensity level.
For an intensity matrix of irregular subfield, the leaf movement direction is decided with the MLC set to an angle by which the leaves move (1) along the shorter field size and (2) along the least intensity gradient direction. However, in some complicated cases, the least intensity gradient direction is ambiguous. The MLC therefore has to set at an angle such that the leaves move along the shorter field size direction. When the beam intensity matrices have regular patterns, the least intensity gradient direction becomes obvious. However, the shorter field size direction is perpendicular to the least intensity gradient. In that case, we suggest the MLC should be set at an angle such that leaves move along the least intensity gradient direction. It is because such arrangement results in the least number of beam segments.
During the matrix reduction process, a residual beam intensity matrix Ak(i, j) defined as the original intensity matrix, A(i, j) minus all the previous MLC beam segments, is calculated. The maximum matrix element Lmax,k in the Ak(i, j) is found to determine the intensity level, dk for the next segment (Equation 2):

Where nint is the nearest integer (10).
3.2. The New Algorithm
Our algorithm used an integer linear program formulation to determine the beam segment with the minimal NS and TNMU (11). The formulation contains two phases (12). The first phase involves in minimizing the beam-on time (Equation 3):

Where T is an upper bound of the photon beam monitor unit, which can be calculated using the maximum number of the summation in each row from the beam intensity matrix A. This upper bound can be written as (Equation 4):

The second phase involves in minimizing the number of beam segments (Equation 5):

Where gt = 1, if an element switches from covered to uncovered, and gt = 0, otherwise.
The value of T is equal to the Z* produced from stage one in Equation 3. The parameter m in Equation 4 represents the number of rows, and the parameter n is the number of columns in the beam intensity matrix A. In reality of radiation dose delivery, there are many restrictions on the MLC leaf position such as collision within or between rows, contiguity, leaf-moving direction, and tongue-and-groove effects. These MLC constraints can be characterized by the binary variables namely, lmnt and rmnt. If the beam intensity element in m and n of A is covered by a left/right MLC leaf, when the tth monitor unit is delivered, lmnt/rmnt is set to 1. Otherwise, it is equal to zero. Xmnt is a binary variable equal to 1 when a monitor unit is delivered through the beam intensity element i and j at period t, and is equal to 0 when the element is covered by either the left or right leaf. In addition, combinations of lmnt and rmnt can be used to reflect different MLC conditions such as leaf collision within a row, between rows, restriction of contiguity, tongue-and-groove effects and leaf motion direction (12).
When the MLC leaves change from one beam segment to the next, all leaves start moving at the same time. However, due to the different travel distances, the leaves do not always stop exactly together. For a Topslane Venus M MLC (11), the leaves are designed to move at the same speed between 10 and 18 mm s−1. The leaf travel time is therefore determined by the leaf having the longest travel distance in the segment. Since leaf travel time can be calculated by finding the maximum leaf travel time from each row, the travel time for the whole leaf sequence is approximately proportional to the LTD (Equations 6 - 8)



Where m is the number rows in A. The two variables Mmt and Nmt represent the left/right leaf edge location. For minimizing the LTD as shown (Equation 9):

Since Equation 6 has absolute values, the related constraint will convert into a mixed integer nonlinear programming. As it is difficult to determine the global optimum, we alternatively cancel the absolute symbol to consider the positive and negative value simultaneously. Equation 6 is therefore transferred into a linear form as (Equations 10


Our improved algorithm can therefore be expressed as follows (Equation 12):

4. Results and Discussion
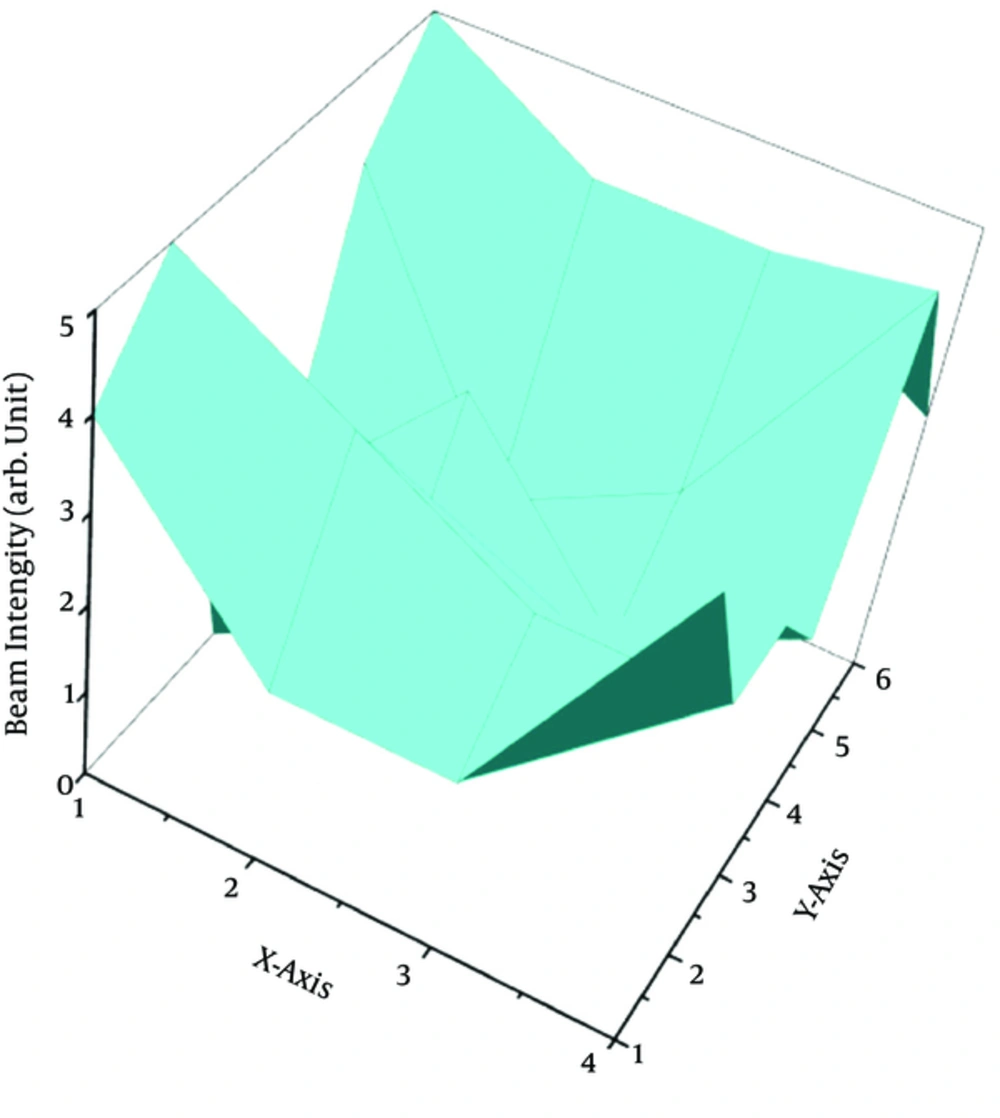
The intensity map in Jing et al. (11) (Figure 1) was used in algorithm comparison. All calculations were performed on a PC equipped with an Intel Core 2 i5-4200 CPU of 1.6GHz, 8G RAM by the linear programming tool Lingo 14.0. Table 1 shows the corresponding results of Xia and Verhey’s, Langer’s (unidirectional and bidirectional) and our algorithm. In our algorithm, we determined the leaf direction according to the principle mentioned in section 3.1.
Plot of the Tested Intensity Matrix in Langer et al. (10)
| Xia’s Algorithm | Langer’s Algorithm (Unidirectional) | Langer’s Algorithm (Bidirectional) | Our New Algorithm | |
|---|---|---|---|---|
| Monitor Unit | 15 | 8 | 8 | 10 |
| Number of segment | 7 | 6 | 5 | 5 |
| Leave travel distance, cm | 24 | 20 | 29 | 7 |
The Number of MU, Segments, and The Distance of Leaf Traveled for Different Algorithms
The three main components in delivery time for the static MLC mode are the beam-on time, verification and recording overhead time (V & R overhead time), and leaf travel time. Beam-on time is the time to irradiate the tumor. V & R overhead time occurs between every single segment and the purpose of verification and recording is to check whether there is any mismatch between the desired and actual leaf positions. The time leaf moves from one position to the next is called leaf traveling time. The delivery time is approximately equal to the sum of the above three components. Different leaf pairs may have various numbers of openings in a delivery process. Since each opening is exposed for unit intensity, all leaf pairs may finish beam delivery at different times. For example, since a Varian MLC requires a minimum separation of 0.2 mm between opposing leaves and the MLC leaves have round ends, the leaf pairs finishing earlier cannot be closed in the opening shaped by the collimator jaws. They have to move further under the jaws. This means that the leaves have to travel extra distances. To address this issue, we proposed a method for simultaneously minimizing the leaf travel distance, TNMU and NS (13).
We calculated 2000 random intensity matrixes ranging from 0 to 5 and specified the field size to be 4 cm × 6 cm. We determined the improving rate from Langer’s algorithm (unidirectional and bidirectional) to our new algorithm (Table 2). We adopted to use three criteria to evaluate the performance of each algorithm with expected values equal to the minimum.
| Average Value | Langer’s Algorithm (Unidirectional) | Langer’s Algorithm (Bidirectional) | Our New Algorithm |
|---|---|---|---|
| Monitor Unit | 7.55 | 7.87 | 6.58 |
| Number of segment | 5.36 | 5.44 | 4.49 |
| Leave travel distance, cm | 17.34 | 12.53 | 6.97 |
Comparison Between Langer’s and Our New Algorithm Using 2000 Random Intensity Maps
Our experimental results showed that our algorithm has significantly better performance than the Langer’s algorithm. In the comparison, only five intensity levels were taken in the beam intensity matrix. Although more intensity levels with higher resolution can increase the dose distribution accuracy, it would at the same time cost more monitor unit and the delivery time. Therefore, the tradeoff between the delivery time and dose accuracy should be evaluated in the treatment.
On the other hands, some MLC constraints in this study may be improved through the advancement of mechanic technology. For example, the leaf-moving direction constraint restricts the MLC leave movement in a single direction. To date, most MLC support bi-directional leave movement. Therefore, constraints of leaf motion direction mentioned in Jing et al. (11) have been ignored in this study. Our algorithm can be applied directly to the MLC systems with different mechanical constraints or with constraints freely be combined.
4.1. Conclusions
In this work, we presented an improved leaf-sequencing algorithm that determines the optimal segmentation possible for delivering an intensity map using the multiple static fields. By comparing with other algorithms by Xia and Verhey, and Langer et al. our new algorithm scored the best results. We expected that our new algorithm can greatly shorten the treatment delivery time. Moreover, the wear-and-tear of the MLC can be improved. It results in a greater patient throughput and a reduction of maintenance cost in the medical linear accelerator.