1. Background
Radiotherapy is treatment with high-energy ionizing radiation for some kinds of cancers. In this procedure the prescribed dose of radiation was applied to damage cancer cells and stop them from growing and dividing. A high degree of accuracy regarding the delivery dose is one major requirement of radiotherapy. According to the international commission on radiation units and measurements, ICRP, the overall accuracy of the absorbed dose required to control a tumour and to avoid complications is 5% (1). Other groups proposed 3% - 4% for uncertainty in delivery dose (2-6). To achieve this level of accuracy, it is necessary to audit all steps of the dose calculation: beam data, dose calculation algorithm and so on. The IAEA has developed a practical test based on TRS430 to verify the accuracy of a dissymmetry system. In radiotherapy, monitor units (MU) or beam-on time are provided to deliver actual dose to a tumour. Error in calculation MU causes dose error and a curve in the treatment. Nowadays, a three-dimensional treatment planning system (TPS) has become common in radiotherapy and therefore verification methods for dose calculation have changed (7). Dose calculation algorithms can be broadly classified. One of the major differences between various dose calculation algorithms is the approximation of the mass stopping power (8, 9). Although Monte Carlo is the most accurate algorithm for dose calculation, it requires a long processing time (10-12). Therefore, other algorithms such as Clarkson and point kernel are used. There are uncertainties in the calculation of dose distribution especially in a heterogeneous situation, small field, or an interface region because of electronic disequilibrium. Over the last decade, pencil beam (PB) algorithms have become the standard for dose calculation algorithms in radiotherapy. Although it has acceptable accuracy and calculation speed, certain limitations of PB algorithms and higher accuracy can be addressed through some kernel-based models (8).
A convolution-superposition algorithm improved estimation of dose in an electronic equilibrium region. A pencil beam convolution (PBC) algorithm considers a narrow pencil beam and uses field intensity fluencies with the kernel that describes dose deposition around the primary photon pencil beam in water.
This study focuses on the dosimetric audit of the Isogray TPS (Dosisoft company) and investigation of the accuracy of its dose calculation algorithms.
2. Objectives
For this purpose an anthropomorphic phantom was used with a set of clinical test cases prepared by the IAEA that covers some typical clinical radiation techniques in three-dimensional radiotherapy.
3. Materials and Methods
All measurements were performed in a hospital with an accelerator (ELEKTA Compact) and photon having a low energy (6 MV) beam. Measurements were performed by an ionization chamber.
3.1. Phantom
This study used a heterogeneous phantom based on a semi-anthropomorphic phantom CIRS thorax 002 LFC. This phantom is used for clinical test measurement of the chest wall and breast. The phantom was designed from tissue, bone and lung equivalent materials and it has holes for dose measurement by an ionization chamber. It consists of a 15 cm thick slice and 15 standard slices with 1 cm thickness. The 30 cm × 20 cm diameter body of Plexiglas (Perspex) has a mass density of 1.17 g/cm3 and relative electron density of 1.003. There is also a cylinder of Teflon as bony vertebra and special fiber as lung that is applied with a relative electron density 1.506 and 0.207, respectively. The phantom contains 10 holes to hold interchangeable rod inserts for an ionization chamber. The holes are numbered as shown in Figures 1 and 2. However the phantom has a limited number of available positions for dose measurements; it has slabs in between that accommodate a film dosimeter and measure dose in two dimensions. The phantom was scanned using a computed tomography (CT) scanner (Somatom Emotion 16-Slice, Siemens) that was calibrated using a special calibration agency. The CT images of the phantom in a DICOM format were transferred to the TPS. These images were used for planning the clinical tests.
Right, Ionization chamber measurements are performed in the 15 cm slice; left, standard slice (13).
Plugs number 1, 2, 3, 4 and 5 are tissue equivalent material, 6, 7, 8 and 9 are equivalent lung material and 10 is bone equivalent material (13).
Electron density relative to the CT number and maximum difference between CT numbers for same relative electron density was 20 Hounsfield units (Hus) (Figures 3 - 10).
Difference Between Calculation and Measurement by Different Algorithms in Test Case No. 1
Difference Between Calculation and Measurement in Point 1-Calculated by Different Algorithms in Case Test 2
Difference Between Calculation and Measurement in Point 3 Calculated by Different Algorithms in Case Test 3
Difference Between Calculation and Measurement Points (5, 6, 10 and Sum Dose for Every Point) by Different Algorithms in Case 4
Difference Between Calculations and Measurement by Different Algorithms in Case 6
Difference Between Calculations and Measurement by Different Algorithms in Case 7
Difference Between Calculations and Measurement by Different Algorithms in Case 8
Percentage of Measurements Resulting Out-Side Criteria agreement for Algorithms
3.2. Clinical Test Cases
A set of clinical test cases as advised by IAEA TEC-DOC 1583 (13) were used to verify the range of basic treatment techniques applied in clinical practice. A detailed description of test cases and measurement points are given in Table 1.
| No. of Case | Description of Test | Reference Point | Measure Point(s) | Agreement Criteria, % |
|---|---|---|---|---|
| Single field, SSD = 100, angle Collimator and Gantry = 0°, size of field = 10 × 10 | 3 | |||
| 3 | 2 | |||
| 9 | 4 | |||
| 10 | 3 | |||
| 1 | 2 | |||
| 5 | 2 | |||
| Oblique incidence, lack of scattering and tangential field, SSD = 100, angle Gantry = 90°, angle Collimator: depended to wedge | 1 | |||
| 1 | 3 | |||
| Significant blocking of the field corner. SSD = 100, technique: SAD. angle Collimator = 45°,filed size 14 × 14 down to 8 × 10 | 3 | |||
| 3 | 3 | |||
| Four field box, technique: SAD. Set-up at point: 5 | 5 | |||
| 5 (0°) | 2 | |||
| 5 (90°) | 3 | |||
| 5 (180°) | 3 | |||
| 5 ( 270°) | 3 | |||
| Ʃ | ||||
| 6 (0°) | 4 | |||
| 6 (90°) | 3 | |||
| 6 (180°) | 4 | |||
| 6 (270°) | 3 | |||
| Ʃ | ||||
| 10 (0°) | 3 | |||
| 10 ( 90°) | 4 | |||
| 10 (180°) | 3 | |||
| 10 (270°) | 4 | |||
| Ʃ | ||||
| MLC block of clinder: 10 cm, technique: SAD, set-up at point: 2, angle Gantry: 0°, angle Collimator: 0° | 2 | |||
| 2 | 3 | |||
| 7 | 4 | |||
| L-shaped field with oblique incidence. Set-up at point:5, technique: SAD, angle Collimator:0°, angle Gantry: 45°, filed size 10 × 20 down to 6 × 12 | 3 | |||
| 3 | 3 | |||
| 7 | 5 | |||
| 10 | 5 | |||
| Plan with asymmetric fields and wedge, technique: SAD. set-up at point: 3 | 5 | |||
| 5 (0°) | 2 | |||
| 5 (90°) | 4 | |||
| 5 (270°) | 4 | |||
| Ʃ | ||||
| Plan with non-coplanar field. technique: SAD, set-up at point: 5 | 5 | |||
| 5 (30°) | 3 | |||
| 5 (90°) | 3 | |||
| 5 (270°) | 3 | |||
| Ʃ |
Agreement Criteria are Listed for Each Test Casea
Eight cases and thirty points comprised the total number of measurements. The plan was for test cases to deliver a 2 Gy dose to the reference point in each case and then the calculated dose was obtained by different algorithms at other points. All of the measurements were performed by an ionization chamber. Due to lack of MLC, test case no. 5 was not performed.
3.3. Dose Calculation Algorithms
Dose calculations were performed for some standard clinical tests with different algorithms to evaluate accuracy; the results were compared to measurements as a gold standard. The evaluated algorithms in this study were divided into two categories:
A) Measurement-based algorithm that includes Clarkson (two types: if manual heterogeneity correction is active named Clarkson* and if as default it is inactive and named Clarkson).
B) Model-based algorithms using point kernel convolution that includes fast-fourier transform (FFT), superposition and collapsed cone convolution (CCC).
These models account for density verification approximately for electrons and photons in lateral.
3.4. Measurements
All measurements were carried out on an Elekta accelerator (Compact model, Elekta Oncology Systems) operating with a photon energy of 6 MV. The 6 MV photon beam was investigated in this study since higher energy photon beams have a less inhomogeneity correction effect (14).
For dose measurements in the phantom, a Farmer type ionization chamber (A19, Standard Imaging Co, USA) with electrometer (Supermax, Standard Imaging Co, USA) were employed. The chamber and electrometer were calibrated at secondary standard dosimetry laboratory (SSDL). For all measurement points, the absorbed dose was determined from ionization chamber measurements using the IAEA TRS 398 dosimetry code of practice (15). Pressure and temperature in each measurement condition were also measured.
3.5. Analysis of the Results
IAEA TRS (430) determines criteria for dose measured (Dmeas) and dose TPS calculated (Dcal) such that differences are normalized to the dose measured at the reference point (Dmeas, ref) for each test case (16) (Equation 1).
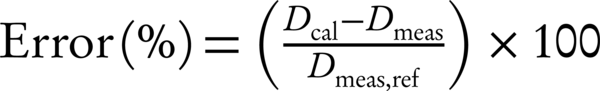
4. Results
In the homogenous media, all of the verification doses determined by algorithms (Clarkson, Clarkson*, Superposition, CCC, FFT) approximately have a highly acceptable degree of agreement between calculations and measurements. For case 1, a single square field, all of the algorithms had acceptable accuracy and their errors were less than the agreement criteria (± 2%). For point 9 in lung equivalent material, the calculated dose was overestimated, however, it was less than the agreement criteria. For point 10 in bone equivalent material, the calculated dose was underestimated. For all algorithms the amount of MU/D was equal to 1.15.
The Clarkson* and Clarkson algorithms had more errors (than) the dose in the tangential beam (case 2). All of algorithms were in compliance with agreement criteria (± 3%). The accuracy of the model-based algorithms (CCC, Superposition and FFT) were equal, and Clarkson* and Clarkson were also equal.
4.1. In Case 3
In this test, all the algorithms overestimated the dose in the field with a wedge, although all of the results in the range were acceptable. The amount of (MU/D) = 1.185 for measurement-base algorithms and for model- based algorithms was equal to 1.181.
In the four fields box test (case 4), the reference point was in the Plexiglas, point 10 in the bone equivalent and the central axis in the vertical beams. Point 6 was in the lunge equivalent material and the central axis in the lateral beams. According to the measurements the Collapsed con, superposition and FFT then Clarkson were accurate, and in some tests, Clarkson failed. The mount of (MU/D) = 1.23 for Clarkson and for point kernels that were model-based was 1.25, the amount MU for the model-base was equal, but the dose calculations in points 6, 10 were different. Accuracy for Collapsed con and Superposition and FFT were close and acceptable, but for Clarkson it was different and for some measurements were higher than the criteria agreement. For the L-shape field (case 6), all algorithms passed, in other words, the amount of error was within the criteria agreement, except for point 7 (in the lunge equivalent material) for algorithm FFT, it was above criteria agreement and failed. Three points were tested, one of them was in plastic water (point 3), where all the algorithms passed and another point was in a lung equivalent media (point 7), where FFT and Clarkson* failed (agreement criteria was 4%). The last point (point 10) was in bone equivalent media, and all of the algorithms passed. In the asymmetrical wedge field (case 7) for model-based algorithms (Superposition, CCC and FFT) the amounts of calculated and measured dose were approximately equal and the amount of error was very small. But for Clarkson, the measured dose was lower than the calculated dose and indicates that Clarkson overestimates the dose, however, Clarkson* underestimates the dose in this case.
In case 8: Deviation outside the agreement criteria was found for Clarkson, and the dose calculation overestimates. For model-based algorithms, in spite of this, the range of agreement was underestimated. For the lateral field, Clarkson and Clarkson* had error that was beyond the agreement criteria.
The result for algorithms being tested for energy of 6 MV is shown in the histogram, and the percentage of results outside of the agreement criteria for all algorithms are shown.
5. Discussion
5.1. Phantom
This study utilized a heterogeneous phantom designed to represent lung, bone and tissue, utilizing equivalent material based on IAEA methodology and previous studies of this phantom. The phantom can be easily shared and transported between hospitals. It is easy to setup and use for testing. More details of the suitability of different phantoms for these types of tests are given (17, 18).
5.2. TPS Dose Calculation Algorithms
The accuracy and quality of TPS depends on the type of algorithms utilized in every step of TPS and has been the topic of numerous studies (19). The results for a homogeneous media comply between measurement and calculated dose. The maximum difference results were: Superposition algorithm (-1.7), CCC (1.8), FFT (-2.1) and for Clarkson and Clarkson* was equal to 3.14, for lateral beam the maximum difference for Superposition was 2.9 and for CCC, FFT, Clarkson and Clarkson* was 3.1, 2.9, 4.7, 6.9 in case test 8, respectively. Except for Clarkson and Clarkson* in the lateral field, the other algorithms passed. Aarup et al. reported good agreement for five algorithms that were tested (20). Clarkson is a simple algorithm that assumes a photon scatter interaction medium. However, it does not include any change in scatter radiation and electron transport in a heterogeneous medium and it cannot consider a linear process due to insufficient accuracy in this algorithm (21). It is acceptable for clinical applications in the cranial and pelvis lesions (22). For our test, although Clarkson had the most diversions, it can be used for clinical tests. A maximum difference calculation dose was seen (3.17%) for equivalent bone material and (4.11%) for equivalent lung material, which underestimates the doses calculated. In the study by Ambolt et al. the Clarkson algorithm has an acceptable degree of agreement between calculations and measurement (23). Linthout et al. also showed good agreement between dose distribution and measured dose by Clarkson algorithm, but for a tissue-air interface the dose calculated by Clarkson overestimates by 12% (24). In test 2 that uses a tangential beam, it calculated an overestimated dose compared to dose measurement. There was a difference (-2.5%) between measurement and calculated dose. The CCC algorithm predicts a dose near to inhomogeneity exactly (25-28). The CCC algorithm as used for the Monte Carlo calculation method and the results show that it has an accuracy of 1% in complex geometries (29). The CCC algorithm had reasonable speed and accuracy in dose calculation (30). One of the limitations in the accuracy CCC is found in a lateral multiple scatter dose (8). The results show that the CCC algorithm predicts in accordance between dose calculation and measurement. Maximum difference was seen in a lung equivalent material (-3.9%) and for a bone equivalent material it was -2.9%, where both results overestimate. Asnaashari showed model-based algorithms have better compliance than measurement-based algorithms (31). Linthout et al. showed the three different calculation algorithms (Clarkson, PB and the Collapsed Cone (CC) algorithms) overestimate the dose in the PTV at the boundary with the low-density tissue, with 12, 10 and 7% for the Clarkson, the PB and the CC algorithm, respectively (24). In another study, Das et al. showed that the Collapsed cone algorithm has better accuracy than the PB algorithm in the interface of inhomogeneous media (27). Nisbet et al. showed Collapsed cone has better accuracy than the PB model in interface lung/tissue and Collapsed cone and the PB model also have inadequate accuracy in interface bone/tissue (25). The maximum deviation was 3.2% for the Sc algorithm in a lung region. Zhang et al. reported that superposition has better accuracy between FFTC and Superposition in the field edge and heterogeneous media (32). In our study FFTC had 3.8% maximum deviation for a lung equivalent media. Vicente et al. showed a 9.7% difference between measured and calculated in cork media with a 6 MV beam by the Superposition algorithm (33). Rutonjski et al. reported a mean 6% deviation with the Superposition algorithm (34). Scholz et al. showed that the Superposition algorithm had a mean 3% difference in various fields (35).
This study applied the methodology described in IAEA TECDOC1583 to perform a TPS audit and evaluate dose calculation algorithms. Maximum deviation was found for the Clarkson algorithm with active heterogeneity correction as a field of interest in (ROI) contouring, and error is reduce. Model-based algorithms had better accuracy, and collapsed cone and Superposition were better. These algorithms help to calculate dose with a higher accuracy.
