1. Background
Spinal disorders (SDs) include a variety of malfunctions in vertebral complex which have been considered as one of the most relevant diseases in the population. SDs can be related to many factors such as occupational conditions, age, weight, etc [1-4], that take considerable costs annually [5]. The origin of pain as the main symptom for SDs may be various and elaborative like muscular spasm, weakness or damage [6], damages due to overstretch or overpressure of the existing soft tissue like intervertebral discs (IVD), fascias, tendons and ligaments [7], vertebral damages [8], and spinal cord stimuli [9]. In SD cases, the motion segment should be immobilized in order to avoid such movements that deteriorate the case and prevent the healing process [10]. The first choice is, hence, fusion of the motion segment by rigid instrumentation [11-15]. Although the level of stress in the components becomes less in rigid fixation systems, several limitations in back natural motions and discomforts emerge. In a retrospective study, it has been shown that the patient have reported various levels of comfort and satisfaction after the surgery and implantation [16-18]. Moreover, immobility of one or more segments endangers adjacent segments due to higher share of loading they received followed by revision or re-intervention [19-25]. These problems have been mastered by using recently-developed systems of fixation, called dynamic stabilization system for the spine [26, 27]. In these designs, the previous rigid rod has been replaced by more flexible alternatives. For needs of flexibility a spring-shaped connector has been used to provide slight but influencing movement between the vertebrae to perform the kinematic tasks [28]. Another dynamic fixation system contains polymer spacer between pedicles screws which covers a wire passes through the holes [28-31]. It has been expected that use of these dynamic systems facilitates the motion of lumbar or thoracic segment underwent fixations.
The dynamic fixation systems, so-called Dynesys, has been employed first by Stoll et al. but then formally introduced by Dubois et al. [27, 32]. Retrospective studies by Cakir et al. showed that Dynesys works slightly better and reduces the operation time and hospital stay, and hence, can be introduced as an effective alternative to fusion in patients [33]. Kim et al. compared the kinematic behavior of spinal fixation systems, including rigid and dynamic ones by virtual human model at the level of L4-S1. They found that the Dynesys system reveal similar kinematic behaviors to the intact model [34]. Cunningham et al. evaluated the safety and efficacy of the Dynesys systems and associated in vitro and in vivo effects in animal models. They used wire and polymer spacer type of Dynesys and concluded that it stabilize spinal motion. Also, 25% rate of screw loosening has been observed after 12 months [29].
Besides the experimental studies, numerical approaches have been further used to examine the efficacy of the dynamic systems of spinal stabilization. Shin et al. developed a finite element model of the human lumbar spine to calculate the stiffness of fixation systems implanted on the levels of L2-L5. Their results showed that dynamic stabilization reveals more similar to the intact model rather than fused fixation [28]. In another study, Zhang et al. conducted a finite element analysis to calculate the biomechanical capacity of dynamic fixation systems in type of wire and polymer spacer and stabilization at the level of L4-L5 and indicated that the stiffness of a segment has been increased in dynamic system, thus, it can significantly diminish the intervertebral disc's stress [30].
Although the efficacy of the fixation systems have been separately studied, no comparative study exists to shed light on the pros and cons of these systems in a fixed model underwent to the same conditions. Moreover, the measures for the efficiency of the fixation systems vary between stress/strain in IVD and vertebrae, or the displacement of the motion segment. Therefore, the present investigation is aimed at compare the prevalent models of spine fixations including rigid, spring-shaped dynamic and polymer spacer dynamic systems in a same model and loading conditions using finite element method.
The principal aim of the present study was to compare the provision of movement facility for the motion segment against reduction in stress of intervertebral disc.
2. Materials and Methods
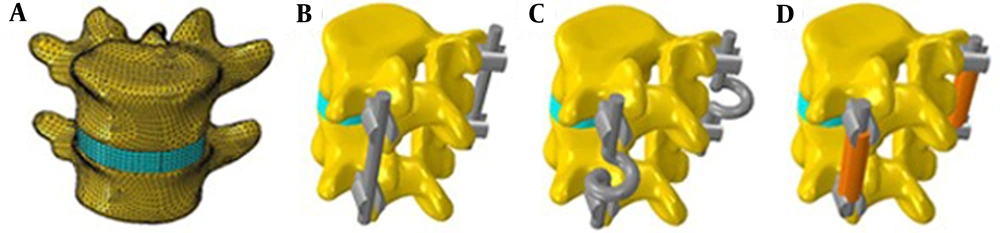
In order to perform a numerical study, three-dimensional models of L4, L5 and IVD have been obtained based on images taken by computed tomography (CT) with thickness of 2.5 mm and 120 kV voltages. A computer-aided design (CAD) software (CATIA, Dassault systeme, version 5R19) has been employed to construct the precise geometry of the motion segment, and also, to design three fixation systems including rigid fixation (RF), spring-shaped dynamic fixation (SDF) and wire and polymer-spacer dynamic fixation (WPDF) which have been inserted into the motion segment model.
The procedure to construct the vertebral geometry included importing cloud point data from CT to the CAD software to form outer surfaces, and then, to make a three-dimensional filled model of L4 and L5 vertebrae. Thereafter, fixations systems have been inserted into the model. Figure 1 illustrates the geometry of motion segment (in meshed view) and stainless steel three fixation systems mounted on it. Vertebral bones and IVD have been considered as homogenous structures which are interconnected together and also with the fixation systems in perfectly-bounded manner. Table 1 presents the material properties of the components used in the simulation. In order to evaluate the effect of fixation systems on a motion segment, lower surface of the proximal vertebra, i.e. L5, has been constrained. In other words, the lower surface of L5 had no possibility to move and it is completely fixed. This assumption is accorded to previous numerical works [28], and the condition of the experiments which fix the lower regions by casts and replicas [29]. Vertical pressure of 1.5 MPa has been imposed on the upper surface of the L4 vertebra as a result of maximum force in upright standing position of a 70-kg man who has worn a backpack with moderate weight. This pressure has been calculated based on the total force exerted to the L4 vertebra by human dynamics software (AnyBody, version 4) divided by area of the L4 vertebral body.
Illustrations of (a) Meshed Model of L4-L5 Motion Segment With IVD, (b) RF, (c) SDF, and (d) WPDF System Mounted on the Model
| Material | Young’s Modulus (MPa) | Poisson’s Ratio |
|---|---|---|
| Bone | 0.27 | |
| Intervertebral disk | 0.48 | |
| Stainless steel | 0.29 | |
| Polymer-spacer | 0.45 | |
| Wire | 0.33 |
Material Properties of the Components Existing in the Models
The models have been discretized into tetrahedral elements. Having achieved the limit of mesh independency RF, SDF and PDF models included 160715, 162522 and 160910 elements, respectively. Maximum size of the element has been set to 2.2 mm. Static solution has been considered in the finite elements analysis in Abaqus software (Abaqus, Dassault Systeme, version 6.10). In fact, previously formed complete models have been imported to the solver software in order to assign material properties, loadings, boundary conditions and finite element network, and finally, calculate displacements and stresses within the models.
3. Results
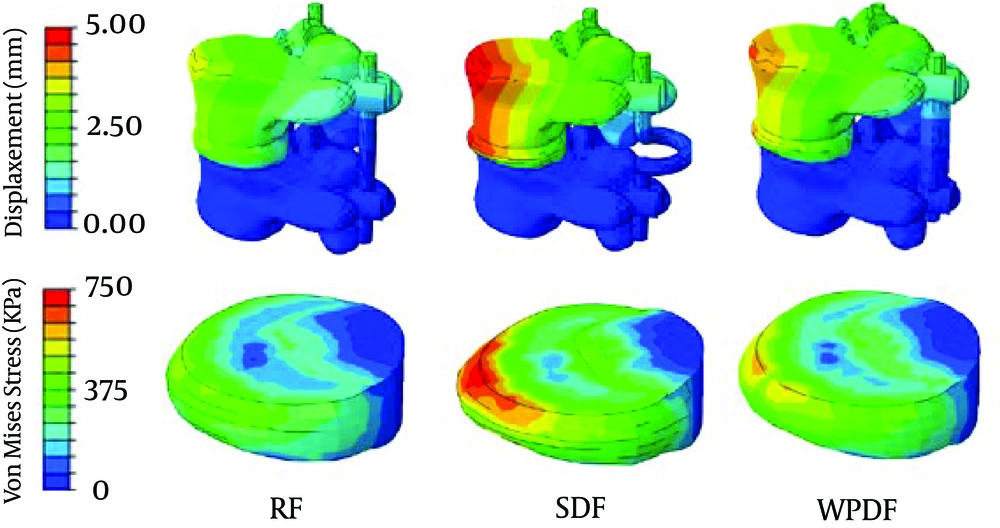
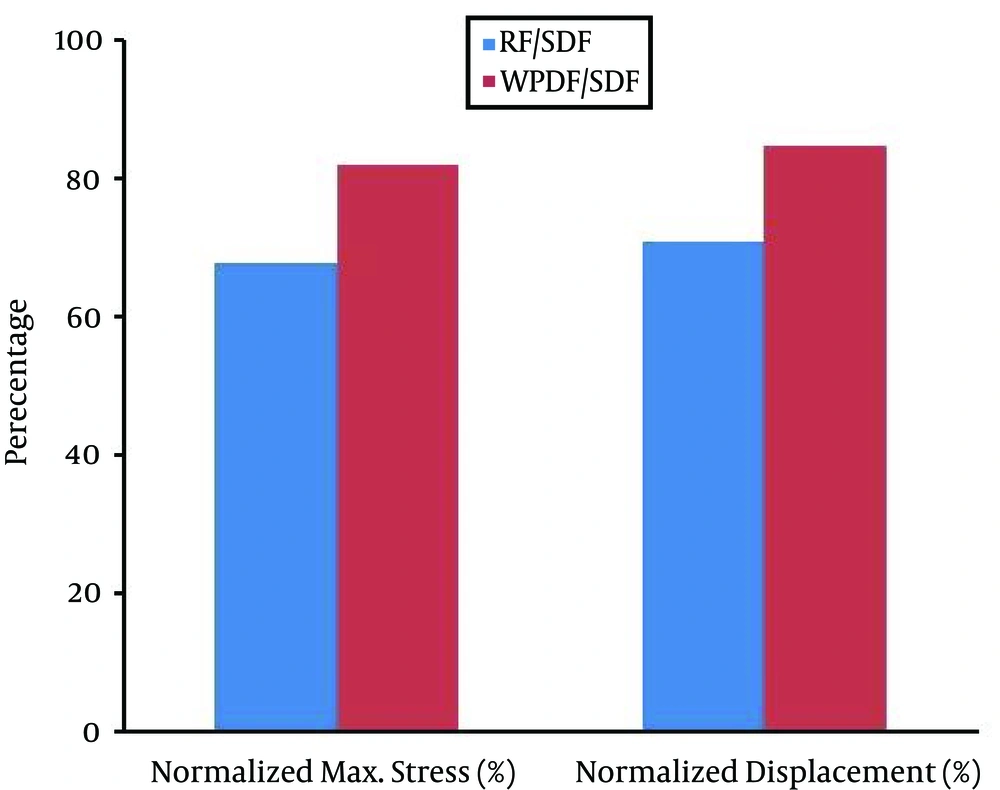
Two principal functions of the fixation systems were to balance stabilization and dynamization of the motion segment, and also, reduce the overpressure on vulnerable tissues like muscles or IVDs. Therefore, overall displacement of the motion segment and stress of the IVD could be considered as measures for efficacy of the fixation systems. Figure 2 presents these contours for 3 models of fixation. Maximum displacement has been revealed in SDF model by amount of 4.95 mm for the top anterior edge of the vertebral body due to the loading. The highest stress value for the IVD is also appeared in SDF model (0.744 MPa). Table 2 develops maximum displacements and von Mises stress values normalized to those of the SDF model in other two models of fixation, also plotted in Figure 3.
Abbreviations: RF, rigid fixation; SDF, shaped dynamic fixation; WPDF, wire and polymerspacer dynamic fixation.
| Model | Normalized Max. Stress | Normalized Displacement |
|---|---|---|
| 67.7 | 70.7 | |
| 82.0 | 84.8 |
Normalized Maximum Displacement and von Mises Stress for RF (Rigid Fixation) and WPDF (Wire and Polymer-Spacer Dynamic Fixation) Models Relative to SDF (Spring-Shaped Dynamic Fixation) Model a
Abbreviations: RF, rigid fixation; SDF, shaped dynamic fixation; WPDF, wire and polymerspacer dynamic fixation
4. Discussion
A finite element analysis on three models of fixation in order to stabilize L4-L5 motion segment have been performed. Evaluated models were rigid, spring-shaped dynamic and wire and polymer-spacer dynamic fixation systems. Maximum displacement for the whole of the motion segment has been observed in SDF model. Single ring structure of the spring between 2 vertebrae has permitted the complex to deflect up to 4.95 mm for the top anterior edge of the L4 vertebra. The RF model has revealed relatively less displacement for the motion segment by 29.3% reduction against the SDF model. Noticeably higher fixation degree of RF system is due to the straight rigid connector rod between the pedicle screws. In such a firm structure a considerable share of the loading energy has been consumed to bend the rigid rod. In RF model the overall displacement of the motion segment is associated with the bending deflection of the straight rod. The WPDF model, on the other hand, has experienced higher displacement in comparison with RF model. It may be confusing that how WPDF with an extra component of polymer-spacer received higher movement; however, noting on the fact that stainless steel rigid connector rod in RF model has been replaced by a wire with different material which possesses the Young's modulus approximately half of the RF rod’s one (Table 1). Thus, the overall resistance of the fixation system against the external loading has been remarkably diminished and maximum displacement in WPDF became 20% greater than in RF model.
Fundamental diversities in these 3 models have led to different behavior of the fixation systems. In RF model rigid rod resists against the loading and the exerted energy has been devoted to bend the rod. In WPDF model, the wire has been strained but the anterior half of the polymer-spacer has been compressed and constrained rising of the movement if the motion segment. In SDF model, loading energy has been consumed to compress the spring ring but since the compression of the spring directly results in shortening of the ring's ends, the overall displacement of the motion segment has been increased up to the maximum value of 4.95 mm. It should also be considered that characteristics of the spring provided in the connector rod in SDF model is of crucial importance in the results. Diameter if the rod, diameter of the ring, number of the rings and density of the rings per length can influence on the stiffness of such a design.
Maximum stress of the IVD has been also occurred in SDF model. Provision of the extreme movement for the motion segment resulted in increase of the stress at the anterior regions of the L4-L5 IVD. The maximum stress with these systems of fixation (0.744 MPa) is less than those reported in another numerical works. For instance, the maximum stress reported for WPDF model by Zhang et al. [30] was roughly 1.5 MPa. The difference between these data originated from the loading on the superior surface of L4 vertebra applied in the present (1375 N) and the mentioned work (2000 N). In general, several experimental studies have reported the IVD stress between the ranges of 0.1 to 0.3 MPa in low loading conditions and varies between 1 and 3 MPa for harsh loadings [35-38].
It has been then concluded that the loading is in medium range of load exertion of the human back. Wilke et al [39]. based on an in vivo experiments reported that the human in relax standing sustains 0.5 MPa in the IVD for healthy individuals. It is to be noted that their experiments considered human in non-weight-bearing condition while the present analysis used loading case of 70-kg man with a backpack of moderate weight, and hence, greater loading has led to increase the stress value from 0.5 MPa in intact segments to maximum 0.744 MPa in segments underwent to fixation systems. An extra finite element analysis with the loading of relax standing has shown that the maximum stress in IVD does not exceed from 0.21 MPa which implies that fixation systems (SDF, for this case) can reduce (by 58%) the overall share of IVD in weight bearing and the main role is performed by the fixation systems.
Several assumptions have been considered in the present numerical analysis. The most important one was to ignore the existence and roles of the muscles acting on vertebral bodies which could also resist against the loading; however, since the goal was to compare the fixation systems, the analysis has neglected them. More, it should be taken into account that loading of analysis was adopted from the case of moderate-weighted backpack. Similar numerical simulations can elucidate the efficacy of such fixation systems in other cases as well.
In conclusion, application of the fixation systems can considerably reduce the load on the IVDs and prepare conditions for healing of the injured IVD. Furthermore, dynamic modes of fixation, i.e. SDF and WPDF, confer possibility of movement to the motion segments in order to facilitate the spinal activities.
