1. Background
Mechanical loads play critical roles on the regulation of the cardiovascular system. One of the most important mechanical stimuli in this system is the blood pressure. Blood pressure induces tension in the arterial wall tissue which is sensed by the smooth muscle cells and the appropriate action such as deposition or degradation of the extracellular matrix is taken [1, 2]. Also shear stress modulates the transport of lipoproteins and macromolecules from blood flow into the arterial wall and therefore directly affects the formation and progression of atherosclerotic plaques [3]. On the other hand arterial wall demonstrates unique mechanical properties such as large elastic deformations, anisotropy and incompressibility [4]. Since the cellular content of the cardiovascular tissue are sensitive to their mechanical environment, the interaction of the mentioned mechanical stimuli with the unique and complex mechanical behavior of the arterial tissue defines the narrow border between the health and disease in cardiovascular system. If we regard cardiovascular diseases as the leading causes of mortality in the world [5], the importance of stated coupling will be multifold. As a result in past two decades, the vital role of biomechanics in prevention, diagnosis and treatment of the cardiovascular diseases is being widely investigated.
Distensibility of the arterial wall due to blood pressure is dependent on its mechanical behavior. This mechanical behavior is dictated by the microstructural architecture of the arterial tissue. Hence, exploring these microstructural features and resulting mechanical behavior contributes to deeper understanding of the cardiovascular patho-physiology [2, 6].
Arterial tissue demonstrates multiscale hierarchical organization. At micro scale, three concentric layers can be distinguished in the arterial wall: intima, media and adventitia (inner, mid and outer layers, respectively). Intima is composed of a single layer of endothelial cells while the adventitia is constructed by loose connective tissue and serves to attach arterial wall to the surrounding tissues and hence, mechanical behavior of the mid-layer mostly determines the mechanical behavior of the arterial wall [2, 7]. On the other hand, microstructure of the media is built of thin and concentric lamellar units. In healthy arterial wall, these lamellar units across media are identical in thickness (~ 12 µm) and fibrous content (elastin 12.7 % and collagen 43.9% of the tissue dry weight) [8, 9], however the orientation of collagen fibers across the arterial media and between lamellar units is variable [10]. It should be noted that the average orientation of the collagen fibers change as we start from the aortic root and progress along the arterial tree. In large arteries near the heart, fibers are mostly oriented in the circumferential direction and change orientation toward longitudinal axis in distal branches, such as femoral artery [10]. Since elastin and collagen fibers are the main mechanically relevant components of arterial media, the orientation of the collagen fibers is a determining parameter in cardiovascular biomechanics [11].
Biological soft tissues exhibit, anisotropic, i.e. direction dependent mechanical behavior, hyperelastic, i.e. elastic response over the wide range of strains up to 60 percent, and incompressible characteristics [7, 9], hence one needs to adopt appropriate theoretical framework for modeling these tissues. Also it should be noted that most of the mentioned mechanical characteristics of the arterial wall are attributed to collagen and elastin fibers of the media.
A popular framework that is capable of capturing such mechanical behavior is strain energy approach [4, 12-14]. In this process, a form of strain energy function (SEF) is proposed, such that its derivative with respect to the strain tensor, provides the mechanical stress. Such SEF is furnished with material parameters which are determined by experimental data for any specific material. These parameters characterize the mechanical behavior of the biomaterial. Obtained material parameters are then implemented into the numerical simulation environment to predict the mechanics of that specific tissue in different physiopathological states (interested reader is referred to the previous paper of the author [15]). It should be noted that FEM simulations are very strong and popular tools in the modeling of the arterial wall mechanics [6, 11, 16].
Blood pressure generates transmural stresses in the arterial media, and the magnitude of these stresses regulate cellular activities. Since the orientation of collagen fibers impacts these stress distributions, in the current research this contribution is investigated and the resulting stress profiles are reported and discussed.
2. Methods
Circumferential stress profile is one of the main determinants of formation or degradation of ECM in the arterial wall. To evaluate this stress profile, different patterns of collagen fiber orientations is built on a regular geometry of arterial wall, then a series of simulations were carried out and the obtained stress profiles are compared accordingly. Such simulations of the soft tissues necessitate the use of nonlinear continuum theories. The details of the modeling and the finite element simulation is provided in the following.
To account for the anisotropic behavior of the arterial wall a previously-described form of SEF [15] is utilized for each region (Eq. 1). In this equation W denotes the SEF, c1, c2, a1, a2 and a3 are material parameters, Ii and Ei denote deformation measures (invariants of the right Green-Cauchy tensor and diagonal components of Cauchy-green strain tensor, respectively). While the first term reflects the isotropic behavior of the ECM, the second exponential term encapsulates the anisotropic response of the arterial wall mechanics originating from collagen fibers. As a result, the material parameters in the exponent represent the role of fiber orientation on the mechanical behavior of the arterial wall in circumferential and axial directions. When the fibers are aligned mostly in the circumferential direction then the material will be much stiffer in that direction compared to the axial direction and hence a1 << a2 and vice versa.
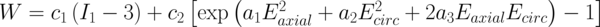
Also is should be noted that when a fiber is making and angle θ with the circumferential direction, its angle with longitudinal axis will be (90 - θ) and the contribution of the fiber elasticity in desired axis is proportional to the cosine of the angle with the intended axis, for example, for a fiber with θ = 30 degrees, its contribution to the stiffness of the circumferential axis is higher compared to longitudinal direction. Based on previously reported values of the material parameters of the above-mentioned strain energy function (refer to [6]), the values of a1 and a2 are estimated.
2.1. Modeling Approach
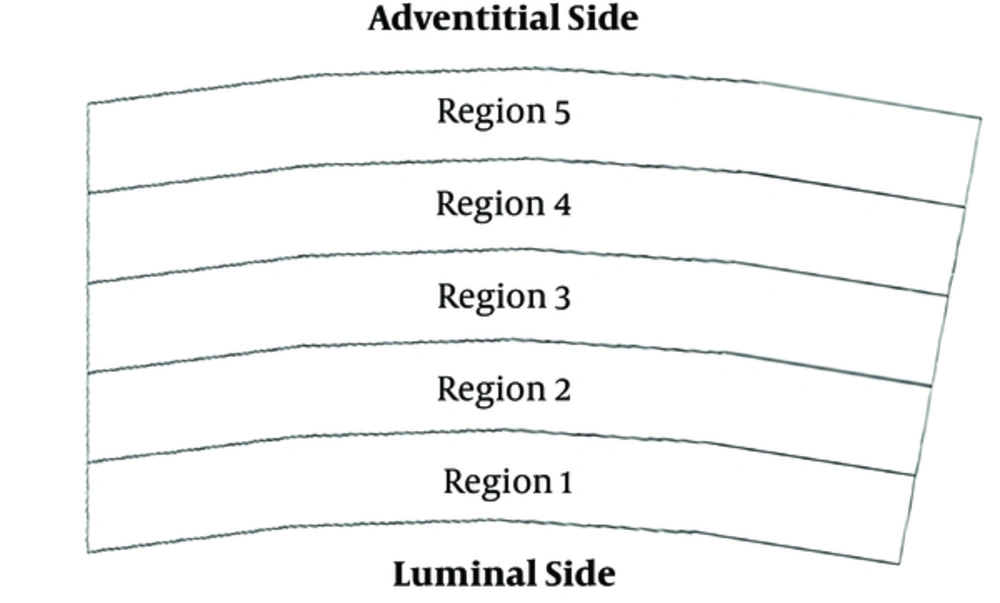
To investigate the effect of fiber alignment on the distribution of the circumferential stress in the artery, a model of the aortic media containing five concentric and interconnected regions were proposed (Figure 1). The aortic media is consisting of approximately 60 lamellar units stacked radially [8], modeled five region denote inner to outer regions of the media and each region represents a group of adjacent lamellar units. These five regions are sufficient to visualize the trend of stress profile across the aortic media. Four patterns of fiber alignment in the proposed model is simulated and resulting circumferential stress profile is compared. Detailed information of fiber alignment for proposed patterns is provided in the following. It should be noted that this information was adopted in the mechanical properties of each region and their contribution were reflected in mechanical properties of the arterial tissue accordingly. In different arteries, the orientation pattern of the collagen fibers is different. Hence, several generic models of the arterial wall with similar dimensions and different orientation of fibers were considered.
2.2. Model I
In this model, fibers are aligned at an angle of 15 degrees to the circumferential axis on the luminal side of the media and this angle is increased with a step of 15 degrees outward. The details of fiber orientation in each region is summarized in Table 1.
| Variables | Orientation of Fibers with Respect to Circumferential Axis, Degrees | |||
|---|---|---|---|---|
| Model I | Model II | Model III | Model IV | |
| Region 5 | 75 | 15 | 30 | 60 |
| Region 4 | 60 | 30 | 30 | 60 |
| Region 3 | 45 | 45 | 30 | 60 |
| Region 2 | 30 | 60 | 30 | 60 |
| Region 1 | 15 | 75 | 30 | 60 |
aThese angles are represented in degrees and measured with respect to the circumferential direction of the artery.
2.3. Model II
Fiber direction in this model is complement of model 1. On the inner region, fibers make an angle of 75 degrees with circumferential direction (or equivalently 15 degrees with longitudinal direction) and this angle is decreased with a step of 15 degrees toward the outer regions (Table 1).
2.4. Models III and IV
These two models are based on constant fiber orientation across the regions. In model III, fibers in all five regions are aligned at an angle of 30 degrees with respect to circumferential direction. This angle for the model IV is 60 degrees with circumferential direction (or similarly 30 degrees with longitudinal axis) (Table 1).
2.5. Finite Element Modeling
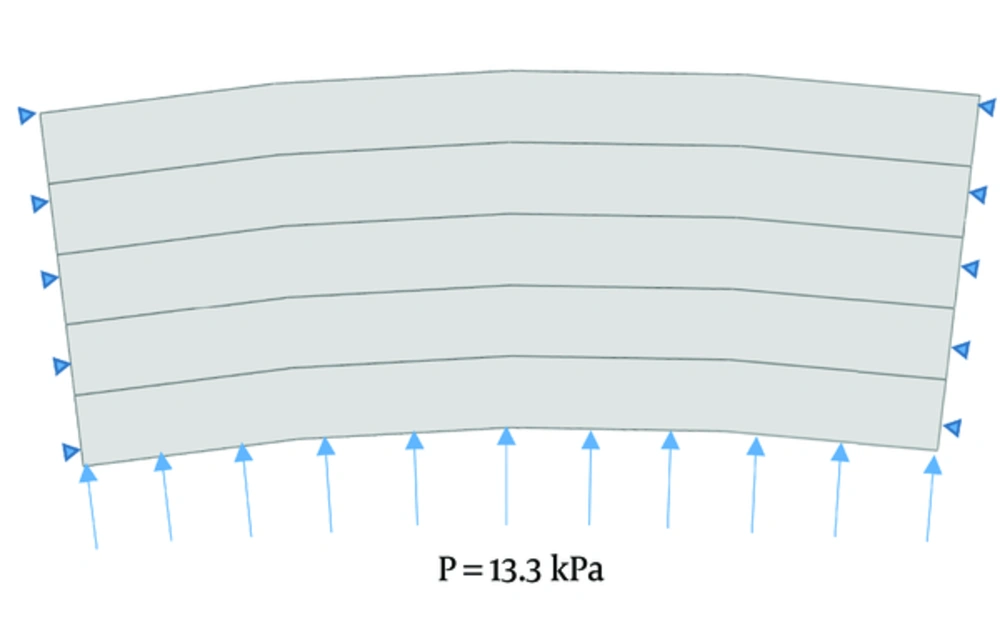
According to the symmetry of the arterial wall geometry, a sector of cylindrical geometry were simulated instead of full cylinder. 2D geometry of the arterial section (circumferential-radial plane) were meshed using 3200 CPE4RH elements and simulated for finite element analysis. It should be noted that mesh independency is checked and selected number of elements are adequate for circumferential stress evaluation. Five concentric regions were distinguished on the geometry to account for changes in the fiber orientation across the thickness. The aortic wall was modeled as a thick-walled and deformable cylinder with inner radius of 5 mm and thickness of 0.5 mm. These dimensions resemble the tunica media of a medium-sized artery in the body.
Symmetric boundary conditions were applied to the model, i.e., the lateral boundaries of the section are restricted in circumferential and longitudinal directions and allowed to displace only in radial direction (Figure 2). Blood pressure of 13.3 kPa applied on the luminal side of the model (Figure 2). Arterial wall was assumed to be stress-free prior to loading. It should be noted that the current study investigates the circumferential stress profile resulting from blood pressure and other mechanical couplings between the blood flow and the arterial tissue, e.g. shear stress and harmonic pressure wave, is not considered (additional detail on the FE simulation is published in our previous paper [2]). It should be noted that circumferential stress is the main component of mechanical stimulus that governs the wall remodeling and stimulate smooth muscle cells to synthesize or degrade extracellular matrix (ECM).
After the simulation, the circumferential stress profile along a radial path from luminal to adventitial side of the media is extracted and compared.
3. Results
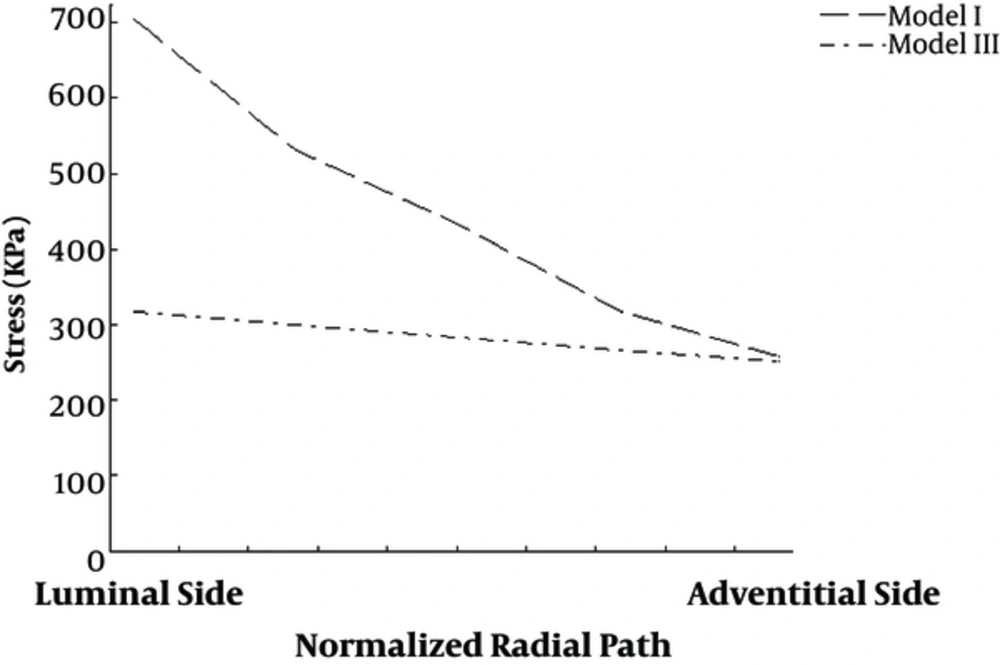
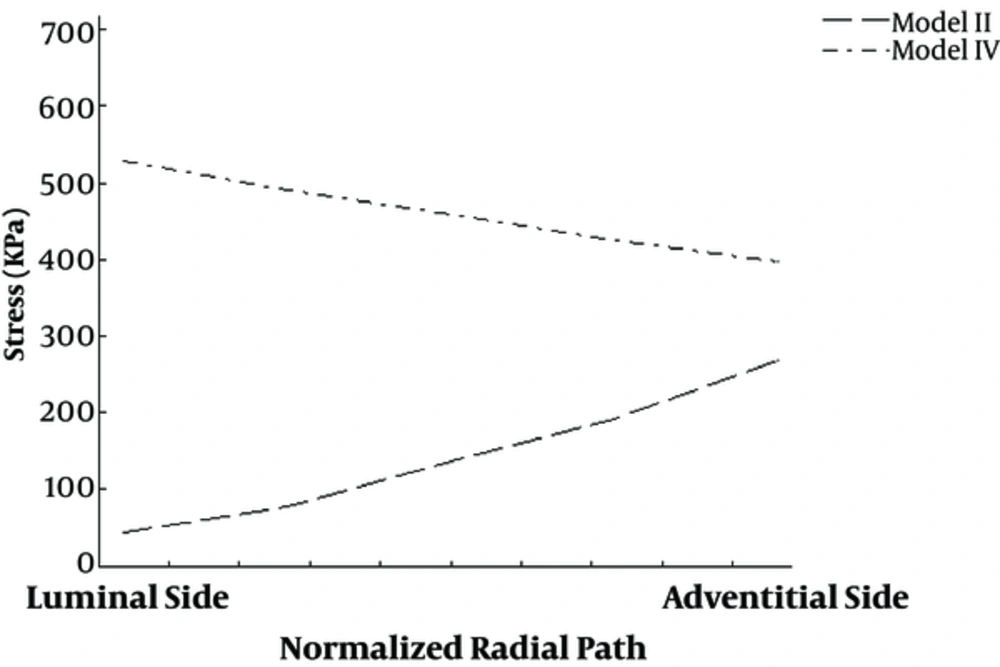
Based on the FE simulations, circumferential stress profile along a radial path for the models were extracted and illustrated in Figures 3 and 4. Models I and III are represented in Figure 3 (models with fibers tending more to circumferential direction on inner side) and model II and IV are shown in Figure 4 (fibers orientation in inner regions is more in axial direction). The nature of stress profiles representing models I, III and IV is descending while the stress profile representing model II is arising as we move from luminal to adventitial side.
Among these curves, models III and IV exhibit a more uniform stress profile. For model III and IV, stress profile deviates around 300 kPa and 500 kPa, respectively. Although, stress profile of the model I and II show a nonlinear trend and more changes in the stress from luminal to adventitial side.
Maximum stress among the models is observed on the luminal side of model I and similarly the minimum stress among models is observed for luminal side of the model II.
4. Discussion
Stress profiles shown on Figures 3 and 4 indicate the vital role of the fiber orientation on the distribution of circumferential stress in the arterial wall. The profile of the circumferential stress in the arterial wall plays an important role on the regulation of ECM [2]. Stresses higher than physiologic range, stimulate the SMCs and lead to formation of new fibers while, stresses below the normal range, cause fiber degradation in order to keep the mechanical stiffness of the arterial wall in the optimal level. Regularly in a pressure vessel, the stress profile is descending (similar to profiles denoting models I, III and IV on Figures 3 and 4), however the specific orientation of fibers can change this trend as seen on Figure 4. Under the luminal blood pressure the circumferential stress in the wall is increased as we move outward. In this model, the fiber gradually change orientation toward circumferential direction and as a result on model II, region 5 (fibers in 15 degrees with circumference) is much stiffer than the inner region 1 (fibers in 75 degrees with circumference) and the profile is ascending. Therefore, focusing on the fiber orientation within the models of the arterial wall is mandatory for better prediction of the biological events in the wall such as remodeling and growth.
The maximum and minimum values of the stress are also reasonable. On model I (Figure 3), the innermost region has fibers aligned at 15 degrees with circumferential direction, hence innermost region of model I is the stiffest among the models and since it is directly exposed to the blood pressure, high stiffness will produce the maximum stress. Also the region 1 on model II (Figure 4) has fibers aligned with an angle of 75 degrees with circumferential axis and hence their stiffness will be less compared to the other models and observing the minimum stress for this region is in agreement with the high impact of fiber orientation on stress profile.
In many of the arterial wall models, the tissue is regarded as a single layer with an overall “preferred direction” [11, 16, 17] (this parameter represents the average orientation of fibers in an specific region of the artery). These models are useful for describing some aspects of arterial wall mechanics, however they are unable to predict and postulate mechanical environment of SMCs across the arterial wall. In the present study, model I and model II have the same overall preferred direction (which is obtained by averaging the fiber direction for each model) but the resulting stress profile is pretty different and somehow contradictory since the former has a descending stress profile and the latter illustrate an ascending stress profile.
4.1. Conclusion
The FE model of the arterial media is simulated and the resulting circumferential stress profile is obtained. This stress profile, acts as a mechanical stimulus that directly invokes biological process such as growth and remodeling. Our findings indicate that circumferential stress profile is highly susceptible to fiber direction and altered fiber direction can even change the descending/ascending nature of the stress profile. Hence, current models of the soft biological tissues that mostly assume the tissue as a single and homogenous layer of connective tissue, neglect some principal characteristics of the arterial wall and cannot reproduce the circumferential stress profile across the arterial tissue. Since the tissue elasticity mostly reflects the physiopathological state of the cardiovascular system, and the respective mechanical behavior is very sensitive to the orientation of fibers across the arterial wall, further investigation and proposition of lamellar models seem necessary for the biomechanical evaluation of growth, remodeling and aging.