Abstract
Objectives:
The objective of this study was to utilize random forest methodology to develop a practical diagnostic function for predicting lymph node metastasis in patients diagnosed with breast cancer.Methods:
The research data of this retrospective cohort study was obtained through a comprehensive analysis of telephone interviews and medical records of 241 patients with breast cancer referred to the hospitals affiliated with Mazandaran University of Medical Sciences between 2016 and 2022. The data analysis method used in this study was random forest analysis to identify the influential factors associated with lymph node metastasis using R software.Results:
The mean age of diagnosis for patients was 52.03 ± 10.932. Based on the random forest analysis outcomes, an accuracy rate of 72.2% has been attained. The influential factors in our study included grade, tubule formation, skin involvement, p53 marker, margin involvement, nuclear pleomorphism, Ki67, tumor location, estrogen receptor (ER), and (progesterone receptor) PR markers. These factors were determined to have a significant impact based on the mean accuracy reduction index. Furthermore, the variables that demonstrated significance based on the mean Gini reduction index included age, grade, tubule formation, tumor size, nuclear pleomorphism, disease level, mitosis, skin involvement, tumor location, and margin involvement.Conclusions:
The utilization of the random forest algorithm, which demonstrates a favorable level of discriminative capability, may serve as a suitable approach for predicting metastasis in patients with breast cancer. Furthermore, by identifying these factors, experts can employ effective strategies to mitigate the condition.Keywords
1. Background
The medical term for the abnormal proliferation of cells within the human body is known as cancer. Every year, a significant number of women succumb to breast cancer. Cancer cells undergo unregulated cellular division and proliferation, forming an anomalous mass called a tumor. Tumors can be classified as either malignant or benign (1). Metastasis, the dissemination of cancer cells to distant tissues, is a significant concern across various types of cancer. Metastasis is the process by which primary tumor cells disseminate and form secondary tumors, subsequently developing additional tumors in different tissues (2). Cancer cells that are present in the breast can invade the lymphatic vessels and initiate growth within the lymph nodes (3). As a result, lymph node evaluation is essential, as the condition of axillary lymph nodes has the greatest influence on cancer recurrence and survival (4). Furthermore, axillary lymph node metastasis is a critical determinant in treatment decision-making and prognosis (5). The literature indicates that patients with breast cancer who have lymph node metastasis have a 40% lower 5-year overall survival rate compared to those without lymph node metastasis. Consequently, precise lymph node status evaluation is critical for the prognosis and treatment of patients with breast cancer (6, 7). This article focused solely on breast cancer, which is widely recognized as the most prevalent health concern affecting women globally. Breast cancer is a leading cause of mortality among women in developed and underdeveloped nations. Consequently, the timely identification and diagnosis of this disease are of utmost importance and should be prioritized (8). According to the estimates provided by the World Health Organization (WHO), breast cancer accounted for approximately one in six global fatalities. In 2018, there were approximately two million new breast cancer cases, making it the most prevalent cancer among women and the second most prevalent cancer globally, following lung cancer (9).
Breast cancer constitutes over 24% of all cancer cases in Iran, with a prevalence rate ranging from 24.8 to 34 per 100,000 women. In 2018, the mortality rate for breast cancer in Iran was less than 10.2 per 100,000 women. In Iran, invasive ductal carcinoma is the prevailing form of breast cancer (10). The standard treatment for breast cancer typically involves a multimodal approach consisting of surgical intervention, radiation therapy, and pharmacological interventions such as hormonal therapy, chemotherapy, and targeted biological therapy (11). In recent years, a significant focus has been on statistical models used to classify medical data based on various diseases and their associated outcomes (12). When employed with data mining techniques, machine learning algorithms have demonstrated the ability to yield significant advancements in medical research, particularly in predicting and diagnosing breast cancer at an early stage (13, 14). Traditional regression techniques often necessitate the fulfillment of specific conditions prior to conducting a comprehensive regression analysis. In recent decades, there has been a notable rise in the adoption of alternative methodologies, such as decision trees and random forests, in medical research. This trend can be attributed to their ability to overcome the limitations commonly associated with classical statistical models and the challenges posed by result interpretation complexity (15).
The random forest algorithm is a commonly used machine learning technique. The random forest algorithm utilizes a multitude of decision trees. It can be stated that a collection of decision trees constitutes a random forest (16). The random forest algorithm offers a potential solution to the overfitting issue commonly encountered in decision trees, resulting in improved accuracy (17). The random forest algorithm performs sampling from the dataset with replacement, where the sample size is equal to the initial volume of the data. A portion of the data is absent from the algorithm, typically accounting for approximately one-third of the total dataset. This subset of data serves as a means to evaluate the algorithm's performance. Randomization is also performed for the variables. Each time this process is executed, a decision tree is generated. A random forest can be created by iteratively performing the decision tree generation process multiple times, such as 400 (18).
The random forest algorithm can enhance the previous method by employing N bootstrap sampling from the dataset. In simpler terms, this algorithm utilizes sampling with replacement to create a sample the same size as the original dataset. As a result, approximately one-third of the total dataset is not included in the algorithm. This particular subset of data is utilized to evaluate and validate the algorithm. A decision tree is generated in each iteration of this process. Repeating the process mentioned above multiple times, specifically 400 times, creates a random forest. In the process of constructing a decision tree, a random sample of m variables is chosen. When splitting the tree, only one of these m variables is utilized rather than all variables. This selection of m variables is performed for each split of the tree. By employing this approach, it becomes feasible to prevent the formation of decision trees where the higher levels consistently incorporate a particular variable solely due to the dominance of that variable, thereby leading to improved outcomes (18, 19).
In the random forest algorithm, randomization is applied to variables and observations, enhancing its robustness against noise and overfitting. The random forest algorithm is employed to develop a reduced complexity model while maintaining effective diagnostic performance for detecting lymph node metastasis in patients with breast cancer (20).
2. Methods
The present cohort study (21) comprised 241 individuals diagnosed with breast cancer. The research data were obtained from the medical records of patients with breast cancer who sought treatment at hospitals affiliated with Mazandaran University of Medical Sciences in Sari City from 2016 to 2022. In order to finalize the data collection process, additional patient information was acquired via telephone communication. The eligibility criteria for participation in the study included a diagnosis of malignant breast cancer.
A checklist validated by thoracic surgeons and breast cancer oncologists was used to collect data. Furthermore, the validity of this checklist has been examined by relevant specialists, and their ideas have been incorporated to correct any flaws and improve the checklist's quality. This checklist has the potential to help us achieve our objectives. The independent and background variables in the checklist were age, marital status, estrogen receptor (ER), progesterone receptor (PR), tumor size, tumor location, stage, P53, Ki67, HER2, skin involvement, margin, DCIS (ductal carcinoma in situ), grade, tubule formation, nuclear pleomorphism, mitosis, and lymph node metastasis. In this investigation, the sample size is at least 200 (five to ten times the number of variables) (22). The final sample size employed in the technique is large and adequate due to bootstrap sampling in the essence of random forest (10). The random forest technique is a non-parametric way of group learning approaches, such as classification and regression trees, and was initially published by Breiman (2001) (23) in the context of machine learning.
In the random forest algorithm, randomization is applied to variables and observations, enhancing its resistance to noise and overfitting (24). Random forest exhibits exceptional performance when it comes to the selection of critical variables or when two indicators, mean decrease accuracy (MDA) and mean decrease Gini (MDG), are utilized (25, 26).
The software utilized in this article is R software. The random forest model was fitted using the randomForest package and the randomForest command. The randomForest package and the rfImpute command were also utilized for imputing missing data. The rfImpute function utilizes a random forest model to train on the available data and subsequently replaces the missing values with the predicted values in an iterative manner. The initial step involves selecting the mean, median, or mode as the initial value for the algorithm used to impute missing data. Subsequently, the random forest fitting process is iterated to obtain the most accurate prediction values for the missing data. Typically, the optimal value for missing data is achieved by applying 5 - 6 iterations of random forest fitting. The crucial aspect of this command is ensuring no missing data in the response variable (27). This study employed random forest techniques to identify factors influencing metastasis to lymph nodes by eliminating irrelevant variables using MDA and MDG indicators.
3. Results
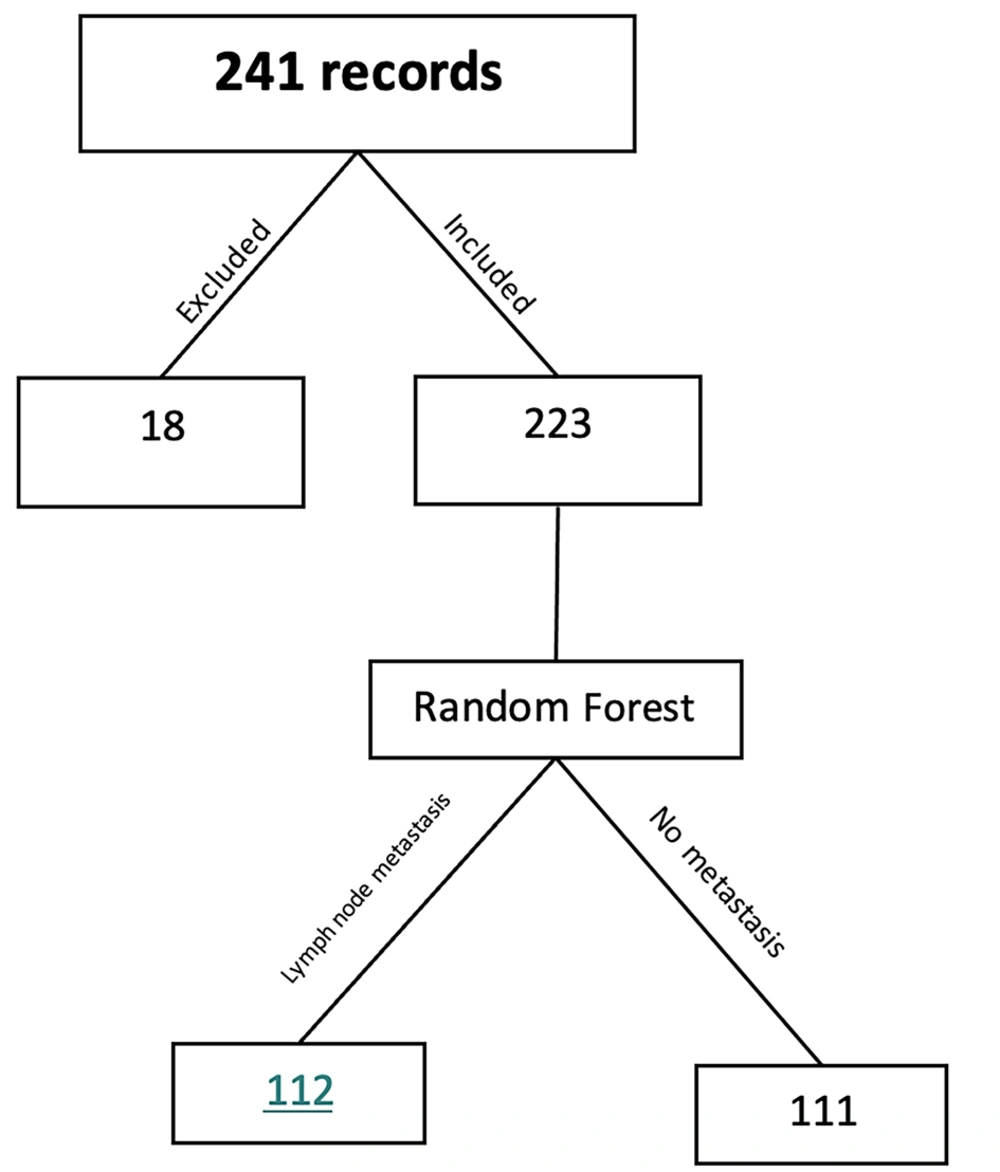
The data for this study were obtained through a comprehensive review of the medical records of 241 female patients diagnosed with breast cancer. The patients were selected from hospitals in Sari, which are affiliated with Mazandaran University of Medical Sciences. As depicted in Figure 1, out of the 241 cases that were examined, 18 were deemed unsuitable for the study on the grounds of omission of essential information, significant data gaps, and other similar factors. A total of 223 cases, accounting for approximately 15% of the cases, were assessed. The mean age at diagnosis for patients was 52.03 ± 10.932. Out of 223 patients diagnosed with breast cancer, 111 had lymph node metastasis, while the remaining 112 had no evidence of metastasis in their lymph nodes. The comparison of the average age of breast cancer diagnosis between the two groups, one with metastasis to lymph nodes and the other without, did not yield a statistically significant result at the 95% confidence level (P = 0.195). This suggests no discernible difference in the average age between the two groups. The descriptive information of the variables is shown in Table 1. The relationship between each variable and the response variable was assessed by conducting the chi-square test for qualitative variables and the t-test for quantitative variables. The P-value for each test is provided in Table 1.
Flowchart of hospital records review
Descriptive Information of the Variables and Chi-Square Test Between the Response Variable and Each Other Variable in Patients with Breast Cancer
| Variables | No Metastasis to Lymph Nodes | Metastasis to Lymph Nodes | 95% CI a for the Test Statistic | P-Value | ||
|---|---|---|---|---|---|---|
| Mean ± SD | Domain | Mean ± SD | Domain | |||
| Age b | 51.3 ± 11.53 | 22 - 86 | 53.17 ± 9.8 | 33 - 74 | (-4.7 - 0.97) | 0.195 |
| Tumor size | 2.3 ± 1.12 | 5 - 0 | 2.5 ± 1.25 | 1 - 8 | (-0.524 - 1) | 0.182 |
| Variables | Quantity and Relation c | P - Value | ||||
| Variable Name | Variable Levels | No Metastasis to Lymph Nodes | Metastasis to Lymph Nodes | Total | ||
| Marital status | Single | 41 (52.6) | 37 (47.4) | 78 (35) | 0.541 | |
| Married | 70 (48.3) | 75 (51.7) | 145 (65) | |||
| Tumor location | 0 (left) | 48 (52.2) | 44 (47.8) | 92 (41.3) | 0.676 | |
| 1 (right) | 61 (47.7) | 67 (52.3) | 128 (57.4) | |||
| 2 (both sides) | 2 (66.7) | 1 (33.3) | 3 (1.3) | |||
| Stage | I | 61 (53) | 54 (47) | 115 (51.6) | 0.502 | |
| II | 45 (47.4) | 50 (52.6) | 95 (42.6) | |||
| III | 5 (38.5) | 8 (61.5) | 13 (5.8) | |||
| ER | 0 (negative) | 25 (45.5) | 30 (54.5) | 55 (24.7) | 0.460 | |
| 1 (positive) | 86 (51.2) | 82 (48.8) | 168 (75.3) | |||
| PR | 0 (negative) | 32 (45.1) | 39 (54.9) | 71 (31.8) | 0.337 | |
| 1 (positive) | 79 (52) | 73 (48) | 152 (68.2) | |||
| P53 | 0 (negative) | 62 (46.6) | 71 (53.4) | 133 (59.6) | 0.251 | |
| 1 (positive) | 49 (54.4) | 41 (45.6) | 90 (40.4) | |||
| Ki67 | 0 (negative) | 33 (55.9) | 26 (44.1) | 59 (26.5) | 0.270 | |
| 1 (positive) | 78 (47.6) | 86 (52.4) | 164 (73.5) | |||
| Her2 | 0 (negative) | 70 (51.9) | 65 (48.1) | 135 (60.5) | 0.442 | |
| 1 (positive) | 41 (46.6) | 47 (53.4) | 88 (39.5) | |||
| Skin | 0 (no involvement) | 97 (48) | 105 (52) | 220 (90.6) | 0.104 | |
| 1 (involvement) | 14 (66.7) | 7 (33.3) | 21 (9.4) | |||
| Margin | 0 (no involvement) | 97 (48.7) | 102 (51.3) | 199 (89.2) | 0.375 | |
| 1 (involvement) | 14 (58.3) | 10 (41.7) | 24 (10.8) | |||
| DCIS | 0 (absent) | 36 (47.4) | 40 (52.6) | 76 (34.1) | 0.872 | |
| 1 (present) | 38 (51.4) | 36 (48.6) | 74 (33.2) | |||
| 2 (DCIS) | 37 (50.7) | 36 (49.3) | 73 (32.7) | |||
| Grade | I | 35 (62.5) | 21 (37.5) | 56 (25.1) | 0.02 | |
| II | 54 (41.9) | 75 (58.1) | 129 (57.8) | |||
| III | 22 (57.9) | 16 (42.1) | 38 (17) | |||
| Tubule formation | I | 18 (56.3) | 14 (43.8) | 32 (14.3) | 0.042 | |
| II | 24 (66.7) | 12 (33.3) | 36 (16.1) | |||
| III | 69 (44.5) | 86 (55.5) | 155 (69.5) | |||
| Nuclear pleomorphism | I | 22 (57.9) | 16 (42.1) | 38 (17) | 0.339 | |
| II | 65 (46.1) | 76 (53.9) | 141 (63.2) | |||
| III | 24 (54.5) | 20 (45.5) | 44 (19.7) | |||
| Mitosis | I | 74 (50.3) | 73 (49.7) | 147 (65.9) | 0.778 | |
| II | 19 (45.2) | 23 (54.8) | 42 (18.8) | |||
| III | 18 (52.9) | 16 (47.1) | 34 (15.2) | |||
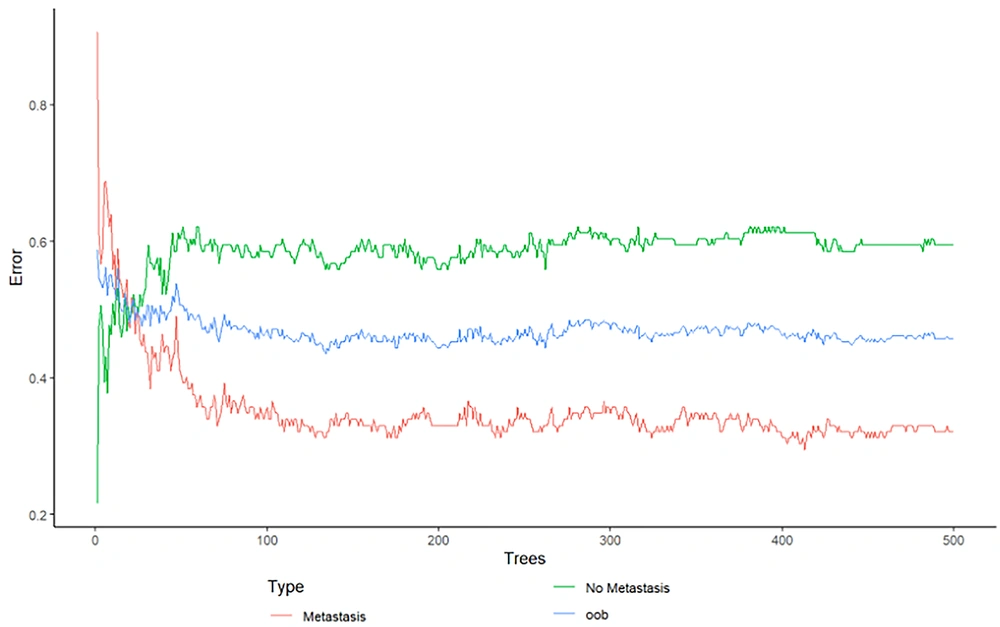
To ensure the optimal fit of the random forest model on the data, it is imperative to determine the optimal values for specific parameters, such as mtry and ntree. The "mtry" argument is a required parameter in the "randomForest" function. As previously stated, randomization is employed in the random forest algorithm, where a subset of m variables is selected from a pool of M variables (M > m). This argument presents the number of variables that have been selected. As previously stated in the introduction, the random forest algorithm comprises many decision trees. The ntree parameter in the randomForest function is utilized to specify the number of trees that constitute the random forest. To effectively determine the optimal parameters for RF (mtry, ntree), the algorithm was executed with varying numbers of variables (features) and trees. Compared to other configurations, A combination was chosen based on its ability to minimize the out-of-bag (OOB) error. Berriman demonstrated the convergence of error as the number of decision trees increases, utilizing the law of large numbers (28). Figure 1 shows that the augmentation in the quantity of decision trees results in a decrease in the OOB error. Figure 2 shows that the OOB error remains constant after approximately 400 trees. This constancy becomes evident at the point of 500 trees. Therefore, running a random forest with 500 trees is adequate for the data.
Out-of-bag error based on the number of trees in the random forest
In order to determine the optimal number of variables, a random forest model was executed with 500 iterations. Table 2 shows that utilizing four variables yields a lower OOB error.
The Results of Optimal Selection of the Number of Variables Argument (Mtry) of the Random Forest Model Based on the Out-of-Bag Error Value in Patients with Breast Cancer
| Number of Variables | Out-of-Bag (OOB) Error (%) |
|---|---|
| 2 | 51.57 |
| 4 | 50.67 |
| 8 | 53.36 |
Finally, two optimal values of 500 for the number of trees and 4 for the number of variables were selected, and the random forest was fitted on the data. Table 3 indicates that this random forest achieves an accuracy of 70%.
The Results of Evaluating the Random Forest Classifier Model in Patients with Breast Cancer
| Number of Variables | Model Accuracy | 95% CI for the Model Accuracy |
|---|---|---|
| Full variables | 0.70 | (0.63 - 0.76) |
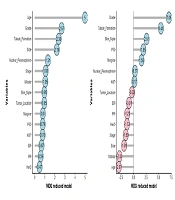
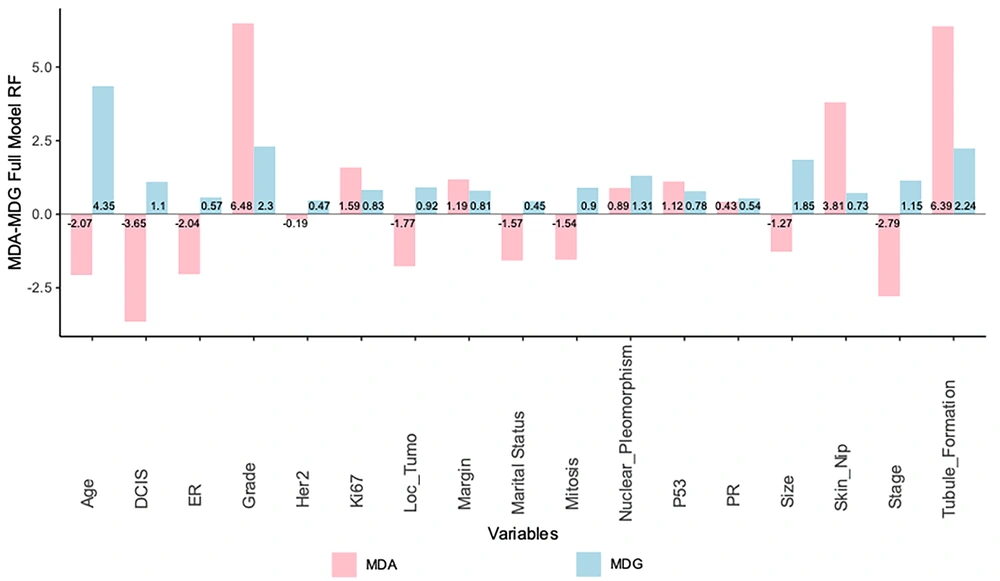
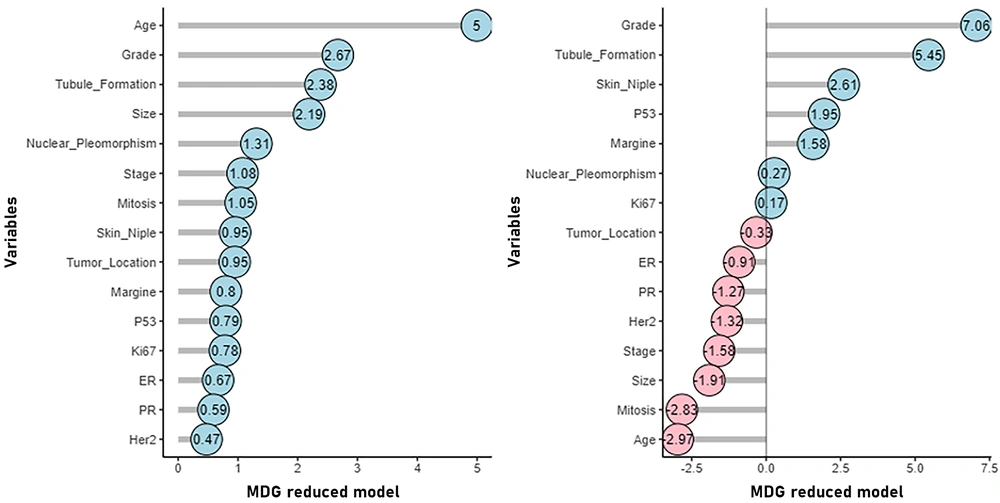
One notable accomplishment of the random forest algorithm is its ability to identify significant variables (24). Comparisons are conducted between the variables using two criteria: MDG and MDA. When evaluating the significance of a variable, it is observed that a lower value of MDG or MDA corresponds to a lower level of significance. In comparison, a higher value of MDG or MDA indicates a higher significance level for that particular variable (29). Figure 3 shows that the variables of marital status and DCIS exhibit the lowest MDG and MDA values, respectively.
The significance of the factors influencing lymph node metastasis based on mean decrease accuracy and mean decrease Gini in patients with breast cancer
It is anticipated that improved accuracy can be attained by eliminating the two variables mentioned earlier and re-fitting the random forest algorithm using the reduced data set. To determine whether the model is predictive, 70% of the data is designated as the training set, and the remaining 30% is designated as the test set. In order to assess the predictive capability of the model, the random forest is fitted to the training and test data in the absence of the two variables mentioned. The accuracy, specificity, and sensitivity of each random forest model are detailed in Table 4, and the disturbance matrix is presented in Table 5.
Joint Disturbance Matrix for Random Forest Model on Reduced Training and Testing Datasets in Patients with Breast Cancer
| The Actual Class of Individuals | Predicted Class in the RF Model in the Training Data Set with Reduced Variables | Predicted Class in the RF Model in The Test Data Set with Reduced Variables | ||
|---|---|---|---|---|
| No Metastasis to Lymph Nodes | Metastasis to Lymph Nodes | No Metastasis to Lymph Nodes | Metastasis to Lymph Nodes | |
| Metastasis to lymph nodes | 0 | 39 | 14 | 59 |
| No metastasis to lymph nodes | 16 | 12 | 55 | 28 |
Random Forest Model Evaluation Results on Two Reduced Training and Testing Data Sets of Breast Cancer Patients a
| The Fitted Model | Data Set | Sample Volume | Accuracy | Specificity | Sensitivity |
|---|---|---|---|---|---|
| Random forest | The training data set with reduced variables | 156 | 73 | 66 | 80 |
| The test data set with reduced variables | 67 | 82 | 57 | 100 |
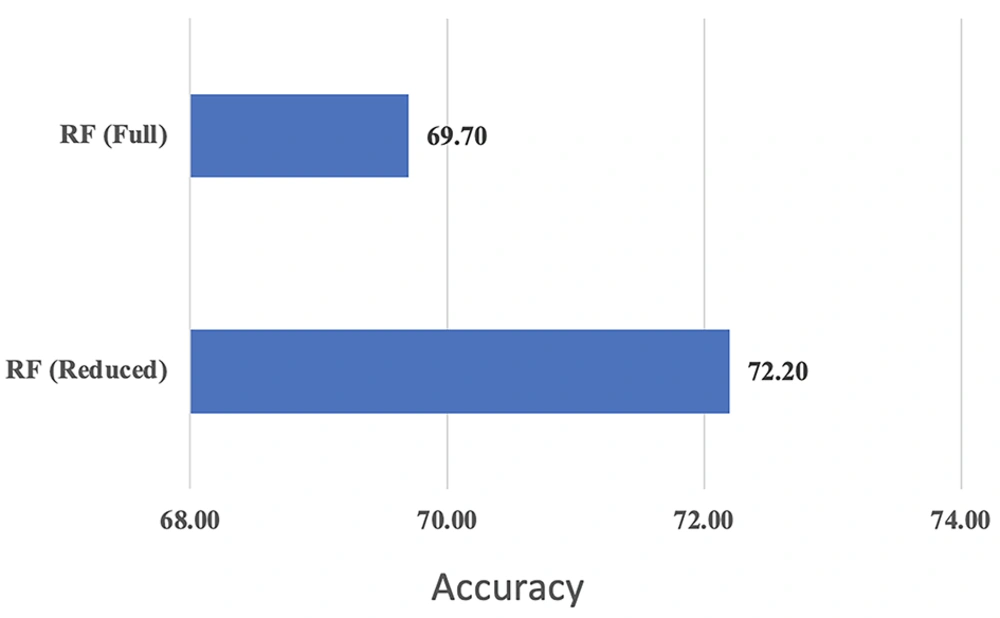
The appropriate predictive potential of the model is demonstrated in Table 5. Therefore, the random forest is re-fitted by removing the two variables of marital status and ductal carcinoma in situ (DCIS) from the entire data set. To compare the performance of two random forests fitted on the original data set with reduced variables and the data set with all variables, the accuracy index was computed and is presented in Table 6. The accuracy index was derived from the disturbance matrices of the two models. The improved accuracy of the random forest with reduced variables (72.2%), as shown in Table 7 and Figure 4, indicates that this version of the random forest is more accurate than the one that includes all variables.
Combined Confusion Matrix for RF (Full) and RF (Reduced) in Patients with Breast Cancer
| The Actual Class of Individuals | Predicted Class in the RF Model with Full Variables | Predicted Class in the RF Model with Reduced Variables | ||
|---|---|---|---|---|
| Metastasis to Lymph Nodes | No Metastasis to Lymph Nodes | Metastasis to Lymph Nodes | No Metastasis to Lymph Nodes | |
| Metastasis to lymph nodes | 92 | 20 | 100 | 12 |
| No metastasis to lymph nodes | 48 | 63 | 50 | 61 |
The Results of the Evaluation of Two Classification Models, RF (Full) And RF (Reduced), in Patients with Breast Cancer
| Variables Present in the Model | Accuracy | 95% CI for Model Accuracy |
|---|---|---|
| All variables | 0.70 | (0.63, 0.76) |
| All variables except marital status and DCIS | 0.72 | (0.66, 0.78) |
The accuracy of RF (full) and RF (reduced) in patients with breast cancer
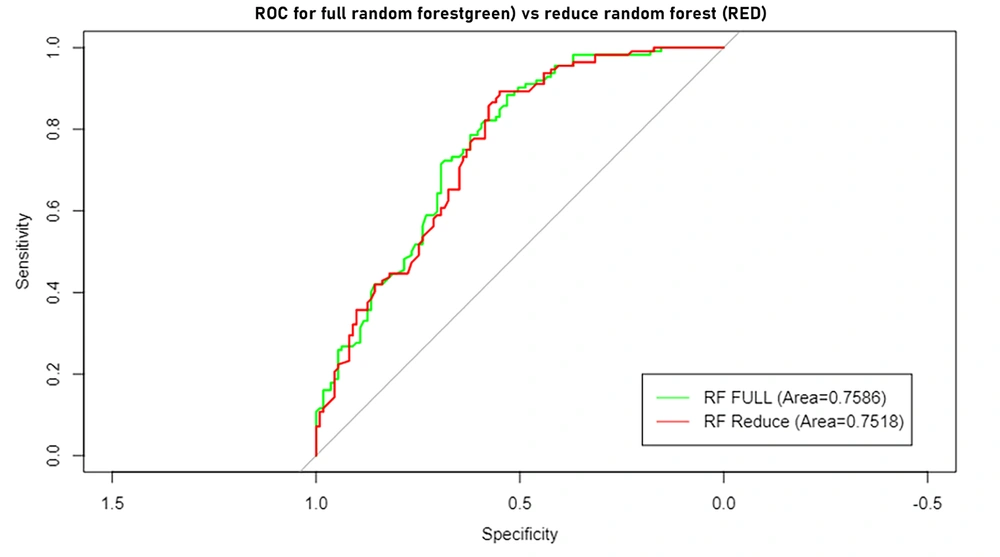
Figure 5 displays the Receiver Operating Characteristic (ROC) curves for the full and reduced variable random forests. The area under the curve for the two specified methods is 0.76 and 0.75, respectively. This indicates that the reduced random forest model performs equally well as the full-variable random forest model.
Receiver operating characteristic for full random forest and reduced random forest
This model employs MDA and MDG methodologies to determine the importance of each influential element. In establishing the priority of influential elements, MDA is superior and more consistent than MDG (30).
As depicted in Figure 6, the RF method reveals that the grade variable holds the highest MDA value (7.06), indicating its utmost significance, followed by tubule formation (5.45), skin involvement (2.60), p53 (1.95), and other influencing variables. According to the MDG, the age variable exhibited the lowest mean decrease and is therefore considered the most significant (4.5). Following this, the variables grade (2.67), tubule formation (2.38), tumor size (2.19), nuclear pleomorphism (1.31), and others were recognized as influential variables.
Determining the importance of variables based on mean decrease Gini and mean decrease accuracy
4. Discussion
Factors accurately predicting a patient's treatment response or progression are paramount in disease treatment studies. As a result, doctors can prescribe medications with more favorable effects and flexibility in treating various disorders. Disease progression can be halted through the management of modifiable risk factors. Classical statistical analysis is frequently used to identify potential dangers. However, there may be restrictions on their use, such as a lack of complete data or an insufficient sample size. Machine learning-based techniques are one novel approach to these issues. This study identified the factors influencing breast cancer metastasis to lymph nodes by fitting the best random forest model to the data. The accuracy of the fitted forest with its corrections was 72.2 percent.
The factors influencing lymph node metastasis in breast cancer were identified based on the results obtained from two indexes, namely MDA and MDG. According to MDA, the initial ten influential factors are grade, tubule formation, skin involvement, p53, peripheral involvement, nuclear pleomorphism, Ki67, tumor location, ER, and PR. According to MDG, the primary factors that influence lymph node metastasis in breast cancer are as follows: Age, grade, tubule formation, tumor size, nuclear pleomorphism, level of disease, mitosis, skin involvement, tumor location, and margin involvement. Identifying the factors influencing lymph node metastasis in this article is also supported by the results of other studies. In summary, we refer to the following studies:
In a study conducted by Jiang et al., machine learning and Shapley algorithms were employed to analyze a cohort of 1 405 breast cancer patients. The findings revealed that tumor size, age, Her2 marker, ER marker, and PR marker were identified as significant factors influencing breast cancer metastasis to lymph nodes. According to the findings of the present study, as indicated by the MDG index, five specific factors have been identified as influential in the process of lymph node metastasis in breast cancer (31). In a study conducted by Purushotham and Venkatesh in 2021, 100 breast cancer patients were examined. The findings revealed a significant correlation between tumor size, grade, and stage and the occurrence of metastasis to lymph nodes in breast cancer. Specifically, the study found that an increase in these three factors was associated with an elevated likelihood of metastasis to lymph nodes (32). In 2021, a cross-sectional study was conducted by Hermansyah et al. to analyze the data from 51 medical records of breast cancer patients. The study revealed a significant relationship between the grade variable and the occurrence of metastasis to lymph nodes in breast cancer, as determined by the chi-square test results. In the present study, the variable "grade" is identified as one of the ten factors influencing breast cancer metastasis to lymph nodes (33). In their study, Li et al. analyzed the medical records of 1131 patients diagnosed with breast cancer. Their findings indicate a significant association between Ki67 expression and various factors, including grade, PR, ER, Her2, and P53. According to our study, the expression of Ki67 and factors such as grade, ER, PR, and P53 marker are among the ten influential factors in breast cancer (34).
Sujarittanakaren et al. discovered a noteworthy correlation between PR, ER, and Her2 markers and the occurrence of metastasis in lymph nodes. Consequently, in cases where it is not possible to assess the status of PR, ER, and Her2 in the primary tumor, evaluating the status of lymph node metastasis can be an alternative method. In the present article, the two markers, ER and PR, have been identified as two of the ten factors influencing breast cancer metastasis to lymph nodes (35). Chand et al. examined 50 cases involving patients diagnosed with breast cancer. Their research findings indicate a significant association between the variable of tumor location and the occurrence of metastasis to lymph nodes. According to the current study's findings, the tumor location variable has been identified as one of the ten influential factors in the metastasis of breast cancer to lymph nodes (36). In a cohort study conducted in 2023, Zahra Zarean Shahraki et al. utilized the random forest algorithm to analyze a sample of 3 580 female patients diagnosed with breast cancer. The study identified tumor status, age at diagnosis, lymph node status, type of surgery, tumor stage, and duration of breastfeeding as the most influential variables for predicting the probability of breast cancer survival. Based on the present study's findings, age and tumor stages have been identified as factors that impact the metastasis of breast cancer to lymph nodes. Consequently, it is probable to consider that the factors that impact the survival of breast cancer patients may also influence the occurrence of lymph node metastasis in these individuals (37). According to Shahrbanu Keyhanian et al., breast cancer is the predominant cancer among women, a significant cause of cancer-related mortality globally. The study revealed that factors such as tumor size and type, histological grade, and the status of estrogen and progesterone receptors were identified as significant determinants of lymph node involvement. Additionally, it was determined that there is no significant correlation between age and the combined status of estrogen and progesterone receptors concerning lymph node involvement. The present study has identified these factors as influential factors in breast cancer (38).
In their study, Dolatkhahi et al. examined the medical records of 5 208 patients at the Cancer Research Center of Shahid Beheshti University of Medical Sciences and Health Services. The researchers employed decision trees, random forests, and support vector machines as machine learning techniques. Their findings indicate that the random forest method achieved the highest level of performance, with an accuracy of 94.75% and a reliability of 97.26%, surpassing the results obtained from the other two methods (39). Kabir Ahmad and Yusoff analyzed a dataset consisting of 700 samples. This dataset included 458 cases classified as benign and 241 as malignant. The objective of their research was to employ random forest as a method for accurately classifying breast cancer lesions through fine needle aspiration (FNA). The researchers discovered that the random forest method, with a precision rate of 72%, demonstrated the ability to effectively classify different types of breast cancer. This approach demonstrates significant potential as a valuable tool for early cancer detection, facilitating the differentiation between malignant and benign tumors (40). In the study conducted by Olivotto et al., it was determined that several factors, including tumor size, margin involvement, tumor grade, and patient age, impact breast cancer metastasis to the lymph nodes. The current study identified the four factors above as part of a comprehensive list of ten factors impacting lymph node metastasis (41).
4.1. Conclusions
The random forest algorithm demonstrates satisfactory accuracy in effectively discerning between different categories. Given the missing data within the study, this algorithm offers a viable approach for effectively handling missing data. The random forest algorithm, which incorporates multiple sampling of variables and their utilization in constituent trees, effectively addresses the issue of small data volume. As a result, it yields accurate and acceptable results from a clinical perspective and in similar studies. It is recommended that medical professionals utilize the random forest model developed in the present study.
References
-
1.
Jeyalatha S, Vishnusri N, Sumbaly R. Diagnosis of Breast Cancer using Decision Tree Data Mining Technique. International Journal of Computer Applications. 2014;98(10):16-24. https://doi.org/10.5120/17219-7456.
-
2.
Aydin Buyruk B, Kebapci N, Yorulmaz G, Buyruk A, Kebapci M. An Evaluation of Clinicopathological Factors Effective in the Development of Central and Lateral Lymph Node Metastasis in Papillary Thyroid Cancer. J Natl Med Assoc. 2018;110(4):384-90. [PubMed ID: 30126565]. https://doi.org/10.1016/j.jnma.2017.07.007.
-
3.
Ashokkumar N, Meera S, Anandan P, Murthy MYB, Kalaivani KS, Alahmadi TA, et al. Deep Learning Mechanism for Predicting the Axillary Lymph Node Metastasis in Patients with Primary Breast Cancer. Biomed Res Int. 2022;2022:8616535. [PubMed ID: 35993045]. [PubMed Central ID: PMC9385356]. https://doi.org/10.1155/2022/8616535.
-
4.
Elshanbary AA, Awad AA, Abdelsalam A, Ibrahim IH, Abdel-Aziz W, Darwish YB, et al. The diagnostic accuracy of intraoperative frozen section biopsy for diagnosis of sentinel lymph node metastasis in breast cancer patients: a meta-analysis. Environ Sci Pollut Res Int. 2022;29(32):47931-41. [PubMed ID: 35543788]. [PubMed Central ID: PMC9252966]. https://doi.org/10.1007/s11356-022-20569-4.
-
5.
Vrdoljak J, Boban Z, Baric D, Segvic D, Kumric M, Avirovic M, et al. Applying Explainable Machine Learning Models for Detection of Breast Cancer Lymph Node Metastasis in Patients Eligible for Neoadjuvant Treatment. Cancers (Basel). 2023;15(3). [PubMed ID: 36765592]. [PubMed Central ID: PMC9913601]. https://doi.org/10.3390/cancers15030634.
-
6.
Chen M, Kong C, Lin G, Chen W, Guo X, Chen Y, et al. Development and validation of convolutional neural network-based model to predict the risk of sentinel or non-sentinel lymph node metastasis in patients with breast cancer: a machine learning study. EClinicalMedicine. 2023;63:102176. [PubMed ID: 37662514]. [PubMed Central ID: PMC10474371]. https://doi.org/10.1016/j.eclinm.2023.102176.
-
7.
Danko ME, Bennett KM, Zhai J, Marks JR, Olson JA. Improved staging in node-positive breast cancer patients using lymph node ratio: results in 1,788 patients with long-term follow-up. J Am Coll Surg. 2010;210(5):797-805 e1. 805-7. [PubMed ID: 20421053]. https://doi.org/10.1016/j.jamcollsurg.2010.02.045.
-
8.
Pati N, Panigrahi M, Patra KC. Evaluation of Different Paradigms of Machine Learning Classification for Detection of Breast Carcinoma. Smart and Sustainable Technologies: Rural and Tribal Development Using IoT and Cloud Computing. Singapore: Springer; 2022. p. 349-56. https://doi.org/10.1007/978-981-19-2277-0_32.
-
9.
Tarlan M, Khazaei S, Madani SH, Saleh E. Prognostic factors for cancer-specific survival in 220 patients with breast cancer: A single center experience. Cancer Rep (Hoboken). 2023;6(1). e1675. [PubMed ID: 35931659]. [PubMed Central ID: PMC9875637]. https://doi.org/10.1002/cnr2.1675.
-
10.
Nafissi N, Khayamzadeh M, Zeinali Z, Pazooki D, Hosseini M, Akbari ME. Epidemiology and Histopathology of Breast Cancer in Iran versus Other Middle Eastern Countries. Middle East Journal of Cancer. 2018;9(3):243-51. https://doi.org/10.30476/mejc.2018.42130.
-
11.
Dhimmar S, Nair A. Breast Cancer Detection Using Classification Algorithms. IRGMETS. 2022;4(7):2582-5208.
-
12.
Tolles J, Meurer WJ. Logistic Regression: Relating Patient Characteristics to Outcomes. JAMA. 2016;316(5):533-4. [PubMed ID: 27483067]. https://doi.org/10.1001/jama.2016.7653.
-
13.
Naji MA, Filali SE, Aarika K, Benlahmar ELH, Abdelouhahid RA, Debauche O. Machine Learning Algorithms For Breast Cancer Prediction And Diagnosis. Procedia Computer Science. 2021;191:487-92. https://doi.org/10.1016/j.procs.2021.07.062.
-
14.
Dinesh P, P K. Medical Image Prediction for Diagnosis of Breast Cancer Disease Comparing the Machine Learning Algorithms: SVM, KNN, Logistic Regression, Random Forest, and Decision Tree to Measure Accuracy. ECS Transactions. 2022;107(1):12681-91. https://doi.org/10.1149/10701.12681ecst.
-
15.
Chao CM, Yu YW, Cheng BW, Kuo YL. Construction the model on the breast cancer survival analysis use support vector machine, logistic regression and decision tree. J Med Syst. 2014;38(10):106. [PubMed ID: 25119239]. https://doi.org/10.1007/s10916-014-0106-1.
-
16.
Biau G, Scornet E. Rejoinder on: A random forest guided tour. Test. 2016;25(2):264-8. https://doi.org/10.1007/s11749-016-0488-0.
-
17.
Ali J, Khan R, Ahmad N, Maqsood I. Random Forests and Decision Trees. International Journal of Computer Science Issues(IJCSI). 2012;9.
-
18.
Williams G. Data Mining with Rattle and R: The art of excavating data for knowledge discovery. New York: Springer; 2011. https://doi.org/10.1007/978-1-4419-9890-3.
-
19.
Smith PF, Ganesh S, Liu P. A comparison of random forest regression and multiple linear regression for prediction in neuroscience. J Neurosci Methods. 2013;220(1):85-91. [PubMed ID: 24012917]. https://doi.org/10.1016/j.jneumeth.2013.08.024.
-
20.
Agarwal S. Data Mining: Data Mining Concepts and Techniques. 2013 International Conference on Machine Intelligence and Research Advancement. IEEE; 2013. p. 203-7.
-
21.
Klebanoff MA, Snowden JM. Historical (retrospective) cohort studies and other epidemiologic study designs in perinatal research. Am J Obstet Gynecol. 2018;219(5):447-50. [PubMed ID: 30194051]. https://doi.org/10.1016/j.ajog.2018.08.044.
-
22.
Tinsley HEA, Brown SD. Handbook of Applied Multivariate Statistics and Mathematical Modeling. Academic press; 2000. 760 p. https://doi.org/10.1016/b978-012691360-6/50002-1.
-
23.
Myles AJ, Feudale RN, Liu Y, Woody NA, Brown SD. An introduction to decision tree modeling. J Chemom. 2004;18(6):275-85. https://doi.org/10.1002/cem.873.
-
24.
Izenman AJ. Modern multivariate statistical techniques. 1. Springer; 2008. 758 p.
-
25.
Wang S, Qian G. variable selection and missing data imputation in categorical genomic data analysis by integrated ridge regression and random forest. arXiv. 2021;preprint.
-
26.
Wang H, Wang C, Lv B, Pan X. Improved Variable Importance Measure of Random Forest via Combining of Proximity Measure and Support Vector Machine for Stable Feature Selection. Journal of Information and Computational Science. 2015;12(8):3241-52. https://doi.org/10.12733/jics20105854.
-
27.
Sage AJ, Genschel U, Nettleton D. Random forest variable importance in the presence of missing data. Random forest robustness, variable importance, and tree aggregation. 2018;37.
-
28.
Breiman L. Random forests. Machine Learning. 2001;45(1):5-32. https://doi.org/10.1023/a:1010933404324.
-
29.
Setargie TA, Tsunekawa A, Haregeweyn N, Tsubo M, Fenta AA, Berihun ML, et al. Random Forest–based gully erosion susceptibility assessment across different agro-ecologies of the Upper Blue Nile basin, Ethiopia. Geomorphology. 2023;431. https://doi.org/10.1016/j.geomorph.2023.108671.
-
30.
Nicodemus KK. Letter to the editor: on the stability and ranking of predictors from random forest variable importance measures. Brief Bioinform. 2011;12(4):369-73. [PubMed ID: 21498552]. [PubMed Central ID: PMC3137934]. https://doi.org/10.1093/bib/bbr016.
-
31.
Jiang C, Xiu Y, Qiao K, Yu X, Zhang S, Huang Y. Prediction of lymph node metastasis in patients with breast invasive micropapillary carcinoma based on machine learning and SHapley Additive exPlanations framework. Front Oncol. 2022;12:981059. [PubMed ID: 36185290]. [PubMed Central ID: PMC9520536]. https://doi.org/10.3389/fonc.2022.981059.
-
32.
Purushotham MK, Venkatesh PM. Association of Histopathological Parameters and Axillary Lymphnode Metastasis in Primary Breast Carcinoma. Asian Pacific Journal of Cancer Care. 2021;6(4):379-82. https://doi.org/10.31557/apjcc.2021.6.4.379-382.
-
33.
Hermansyah D, Pricilia G, Azrah A, Rahayu Y, Paramita DA, Siregar ES. Correlation between Grading Histopathology and Sentinel Lymph Node Metastasis in Early Breast Cancer in University of Sumatera Utara Hospital. Open Access Macedonian Journal of Medical Sciences. 2021;9(B):679-82. https://doi.org/10.3889/oamjms.2021.6423.
-
34.
Li M, Xu H, Deng Y. Evidential Decision Tree Based on Belief Entropy. Entropy. 2019;21(9). https://doi.org/10.3390/e21090897.
-
35.
Sujarittanakarn S, Himakhun W, Worasawate W, Prasert W. The Case to Case Comparison of Hormone Receptors and HER2 Status between Primary Breast Cancer and Synchronous Axillary Lymph Node Metastasis. Asian Pac J Cancer Prev. 2020;21(6):1559-65. [PubMed ID: 32592349]. [PubMed Central ID: PMC7568873]. https://doi.org/10.31557/APJCP.2020.21.6.1559.
-
36.
Chand P, Singh S, Singh G, Kundal S, Ravish A. A Study Correlating the Tumor Site and Size with the Level of Axillary Lymph Node Involvement in Breast Cancer. Niger J Surg. 2020;26(1):9-15. [PubMed ID: 32165830]. [PubMed Central ID: PMC7041355]. https://doi.org/10.4103/njs.NJS_47_19.
-
37.
Zarean Shahraki S, Azizmohammad Looha M, Mohammadi Kazaj P, Aria M, Akbari A, Emami H, et al. Time-related survival prediction in molecular subtypes of breast cancer using time-to-event deep-learning-based models. Front Oncol. 2023;13:1147604. [PubMed ID: 37342184]. [PubMed Central ID: PMC10277681]. https://doi.org/10.3389/fonc.2023.1147604.
-
38.
Keihanian S, Koochaki N, Pouya M, Zakerihamidi M. Factors affecting axillary lymph node involvement in patients with breast cancer. Tehran University of Medical Sciences Journal. 2019;77(8):484-90.
-
39.
Dolatkhahi K, Azar A, Karimi T, Hadizadeh M. Diagnosing Breast Cancer by Machine Learning. Payavard Salamat. 2021;15(4):340-52.
-
40.
Kabir Ahmad F, Yusoff N. Classifying breast cancer types based on fine needle aspiration biopsy data using random forest classifier. 2013 13th International Conference on Intellient Systems Design and Applications. IEEE; 2013. p. 121-5.
-
41.
Olivotto IA, Jackson JSH, Mates D, Andersen S, Davidson W, Bryce CJ, et al. Prediction of axillary lymph node involvement of women with invasive breast carcinoma. Cancer: Interdisciplinary International Journal of the American Cancer Society. 1998;83(5):948-55. https://doi.org/10.1002/(sici)1097-0142(19980901)83:5<948::Aid-cncr21>3.0.Co;2-u.