Pre-transplant Predictive Factors in Multiple Myeloma Patients Undergoing Autologous Stem Cell Transplantation Using Defective Cure Models

Leila Jabari Nanva; Ahmad Reza Baghestani; Dariush Kadkhoda; Ali Akbar Khadem Maboudi

doi:10.5812/ijcm-143873

https://doi.org/10.5812/ijcm-143873

Pre-transplant Predictive Factors in Multiple Myeloma Patients Undergoing Autologous Stem Cell Transplantation Using Defective Cure Models

authors:

Leila Jabari Nanva ¹ , Ahmad Reza Baghestani ¹ , Dariush Kadkhoda ¹ , Ali Akbar Khadem Maboudi ^{1
, *}

1 Department of Biostatistics, School of Paramedical Sciences, Shahid Beheshti University of Medical Sciences, Tehran, Iran

International Journal of Cancer Management: Vol.17, issue 1; e143873

published online: January 4, 2025

article type: Research Article

received: February 26, 2024

revised: December 2, 2024

accepted: December 4, 2024

How To Cite? Jabari Nanva L, Baghestani A R, Kadkhoda D, Khadem Maboudi A A. Pre-transplant Predictive Factors in Multiple Myeloma Patients Undergoing Autologous Stem Cell Transplantation Using Defective Cure Models. Int J Cancer Manag. 2024;17(1):e143873. https://doi.org/10.5812/ijcm-143873.

Abstract

Background:

Multiple myeloma (MM) is a hematologic malignancy that leads to kidney failure, anemia, infection, and severe bone pain due to the presence of bone lesions. Combining antagonists with immunomodulating drugs has resulted in higher survival rates for patients. As a result, many patients receiving appropriate treatment can now achieve long-term survival or even be considered cured. In such cases, it is essential to use cure models to achieve accurate and reliable results with minimal bias.

Objectives:

The study is focused on identifying the factors that predict the response to autologous hematopoietic stem cell transplantation (ASCT) and estimating the cure fraction of MM patients from ASCT to death using cure models.

Methods:

This cohort study involved 77 patients diagnosed with MM, who received ASCT and were followed for 12 years. Patients’ overall survival and cure fraction were analyzed, using defective cure models. The patients’ age and clinical conditions, including Thrombocytopenia, leukopenia, anemia, and blood creatinine levels, were considered predictive factors extracted from the pre-transplantation blood tests.

Results:

The 5-year survival rate of patients was 67.9% and long-term survival was 59.5% in this study. The Inverse Gaussian model estimated the cure fraction at 54.4%, while the Kumaraswamy Inverse Gaussian model estimated it at 24%. The Inverse Gaussian model indicated that the age of the patients and the pre-transplant platelet count were significant factors (P < 0.05). Patients with less than average platelets had a cure fraction of 36%, indicating a lower chance of survival than patients with normal platelets, who had a cure fraction of 54%.

Conclusions:

The Kaplan-Meier curve has a horizontal portion that estimates the number of survived patients. After approximately 6 years and 5 months, the Kaplan-Meier curve flattened, and the estimated cure fraction was 58.5%. The Inverse Gaussian model demonstrates superior accuracy in estimating the cure fraction and identifying predictive factors that affect pre-transplantation survival rates. In this model, the cure fraction was estimated at 54.4%. So, this model warrants more attention. The study suggests low platelet count (thrombocytopenia) reduces patients’ long-term survival. Among patients with Thrombocytopenia, younger patients have a higher long-term survival rate than older patients. As a result, it is recommended to prioritize the care of patients over 60 with Thrombocytopenia to improve their survival rate and reduce mortality.

Keywords

Multiple Myeloma Cure Fraction Cure Models Inverse Gaussian Distributions

1. Background

Multiple myeloma (MM) is a hematological malignancy with the uncontrolled growth of plasma cells due to mutagens (1). Multiple myeloma accounts for about 10% of Hematologic Neoplasms (2). In 2020, the World Health Organization (WHO) reported 176,404 new cases of MM globally, resulting in 117,077 deaths. In Iran, there were 1,092 new cases of MM in the same year, leading to 930 deaths (3). The incidence rate of MM is 6.63, its mortality rate is 3.04 per 100,000 people, and the 5-year survival rate of this disease is estimated at 58.3 (4). The incidence of MM is almost twice as high in black people than in other races (5). The MM is more common in men than women (6). According to the definition of the National Comprehensive Cancer Network (NCCN), MM is divided into MGUS, smoking myeloma (without symptoms), or MM (with symptoms) (7). Cytogenetic abnormalities and frequent intraconal heterogeneity are present in almost all patients and are among the influential factors in patients’ survival. Monoclonal gammopathy of undetermined significance (MGUS) is a precancerous stage that usually does not display any symptoms; almost all MM patients have experienced it before the onset of the disease. Several factors, including genetic factors, cause MGUS to progress to active MM (8, 9). Bone pain is a common symptom of MM, which is accompanied by other symptoms like weakness in arms and legs, fatigue, unexplained weight loss, and fever (10). Over time, symptoms of MM worsen, and common complications of MM include hypercalcemia, kidney failure, infection, skeletal lesions, and anemia (11, 12).

The type of treatment depends on various factors, such as the patient’s condition, age, overall health, and genetic factors. The treatment approach may vary for newly diagnosed patients versus those with relapsed disease. Treatments include immunomodulatory drugs (IMiDs), proteasome inhibitors (PI), monoclonal antibodies, chemotherapy, and stem cell transplantation. Targeted therapeutics such as thalidomide, lenalidomide, and bortezomib have increased overall survival. Chemotherapy improves clinical symptoms and increases overall survival but does not completely cure the disease (13, 14). In recent years, Hematopoietic stem cell transplantation (HSCT) has been an effective therapy for hematological neoplasms, leading to decreased mortality and increased survival (15). Several randomized trials have introduced HSCT as the standard treatment for MM due to its high complete response, event-free survival, and more prolonged (16, 17). However, some patients may have complications, including graft recurrence, graft failure, renal dysfunction, and antibody production (1, 16), explore the profound potential of Autologous Hematopoietic Stem Cell Transplantation (ASCT), when combined with high-dose melphalan, elevate remission rates, and extend overall survival in MM (18).

The main objective of survival analysis is to develop models that predict the time until an event occurs and to create precise methods for identifying the factors that influence this duration. This involves utilizing semi-parametric and parametric approaches (19). With the advancements in cancer treatment, some patients can now survive cancer, and these individuals are referred to as the cure fraction or the long-term survivor (20). Cox or the log-rank test is inappropriate since it ignores the cure fraction and leads to bias in the estimates (21). In this paper, cure fraction modeling is of interest.

Due to the importance of cure fraction models, different approaches have been proposed to estimate its values (22). One of the ways to model the cure fraction is to use defective distributions. Inverse Gaussian distribution (23) is the distribution that can be transformed into a defective distribution by changing the domain of their parameters. Based on the valuable properties of the family of Kumaraswamy distributions, the defective Kumaraswamy inverse Gaussian distribution is produced, which has more flexibility to estimate the cure fraction (24). Different studies have been conducted on the factors affecting the success of transplantation and the survival of MM patients. However, due to individual differences and other factors related to patients, general and comprehensive results have yet to be obtained (25, 26).

2. Objectives

The study aims at identifying predictive factors affecting the overall survival of MM patients and determining the cure fraction based on the pre-transplantation blood test. In upcoming clinical studies, it aims at utilizing cure models to estimate the cure fraction and determine predictive factors for MM patients. This study expands on our prior research, which examined and compared new cure models based on the Kumaraswamy family distribution.

3. Methods

3.1. Participants and Procedures

The present paper is continued research of the previously published article (27) on a retrospective cohort study that was conducted at Taleghani Hospital, affiliated with Shahid Beheshti University of Medical Sciences in Tehran. The study involved MM patients, who were eligible for ASCT using targeted sampling. The patients signed the consent forms after the study's purpose, design, and protocol were explained to them. The study involved 86 patients diagnosed with MM, who underwent ASCT between January 2011 and August 2016. The diagnosis of MM was confirmed through blood tests and biopsy. Patient information was recorded for follow-up, and the survival status of patients was followed until February 2022 through file review and phone calls. To ensure accuracy, 9 patients with incomplete data or those who died of causes unrelated to MM were excluded, leaving 77 eligible patients in the study. For patients who were still alive at the end of the research or whose survival status was not available at the time of follow-up, their records were considered censored.

Regarding survival analysis, the event of interest is death from MM. Therefore, the overall survival time from ASCT to death from MM (in years) was considered the response variable. Risk factors affecting patient survival were reported based on a significance level of 0.05 (P < 0.05).

Deficiencies in red and white blood cells and platelets are common in individuals with MM, leading to various symptoms. The most important of these are anemia, leukopenia, and Thrombocytopenia. Anemia is a medical condition characterized by a low red blood cell count and can lead to symptoms such as weakness, decreased stamina, shortness of breath, and dizziness. Leukopenia occurs when the number of white blood cells (WBC) in the body is low, which may weaken the immune system. Thrombocytopenia is a medical condition that occurs when the platelet count in the blood is lower than usual, which can cause heavy bleeding (26). Predictive factors affecting overall survival with ASCT were investigated through blood tests, including creatinine level, platelet count, WBC, and hemoglobin (Hb) level; the age of patients is also one of the effective factors.

3.2. Statistical Analysis

Cure models are survival analysis models, in which the proportion of cured people is of interest. If there is a cure, the survival function becomes horizontal before the end of the study, which can be recognized by drawing the Kaplan-Meier diagram. The horizontal part of the graph shows that with the increase in study time and proper treatment of patients, many of them have survived, and these people are considered cured (20).

Using Inverse Gaussian and Kumaraswamy Inverse Gaussian distributions, we analyzed the effect of predictive factors on overall survival time. Survival function for Inverse Gaussian distributions (28, 29) and Kumaraswamy Inverse Gaussian distribution (23, 30, 31) is defined in Equations 1 and 2.

Inverse Gaussian survival function (Equation 1):

s (t) = 1 - [Φ (\frac{- 1 + a t}{\sqrt{b t}}) + \exp \{\frac{2 a}{b}\} Φ (\frac{- 1 - a t}{\sqrt{b t}})]

Kumaraswamy inverse Gaussian survival function (Equation 2):

S (t| x) = {(1 - {[ϕ (\frac{- 1 + a t}{\sqrt{b t}}) + e^{\frac{2 a}{b}} ϕ (\frac{- 1 - a t}{\sqrt{b t}})]}^{r})}^{u e x p (β^{'} x)}

t > 0, a < 0, b > 0, u > 0.

The appropriate model was selected based on the criteria of AIC and BIC. The cure fraction for the model is computed based on the Inverse Gaussian distribution in (3) and the Kumaraswamy Inverse Gaussian distribution in (4) (Equations 3 and 4) (24).

p = \underset{t \to \infty}{limS} (t) = 1 - e^{\frac{2 a}{b}}

p = \underset{t \to \infty}{limS} (t| x) = p^{\exp (β^{'} x)}

In this study, Inverse Gaussian and Kumaraswamy Inverse Gaussian regression models were fitted to the data. All reported confidence intervals (CI) are 95%. The data analyses were conducted, using R software, version 4.2.3 (32). The P value was considered less than 0.05 (P < 0.05).

4. Results

Generally, 77 patients with MM, who received ASCT, were analyzed, using defective cure models. The study included 39 male patients (50.6%) and 38 female patients (49.4%). The patients' median age at transplantation was 54 years, with an average age of 54.7 years (SD = 8.0) (Table 1). The time between ASCT and death due to MM is considered overall survival (OS).

Table 1.

Patient Characteristics

Variables	Men	Women	Total
Age	8.32 ± 56.26	7.45 ± 53.19	8 ± 54.74
Overall survival (y)	0.63 ± 6.99	0.69 ± 8.22	0.51 ± 7.75
Leukopenia	3 (3.9)	8 (10.4)	11 (14.3)
Thrombocytopenia	3 (3.9)	3 (3.9)	6 (7.8)
Anemia	15 (19.5)	21 (27.3)	36 (46.8)
Age ≤ 54	12 (15.6)	20 (26)	32 (41.5)
Age > 54	27 (35.1)	18 (23.4)	45 (58.5)
Total	39 (50.6)	38 (49.4)	77

^a Values are expressed as mean ± SD or No. (%).

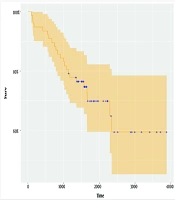
The mean OS was 7.7 years [CI: 6.7 - 8.7]. The 5-year survival rates are estimated at 6.7 years [CI: 7.5 - 10.0]. The horizontal part of the Kaplan-Meier curve indicates the patient who survived or the cure fraction (24). After approximately 6 years and 5 months, the Kaplan-Meier curve became horizontal, and the cure fraction was estimated at 58.5% [CI: 45.2 - 78.5] (Figure 1).

Figure 1.

Kaplan-Meier of overall survival

Table 2 reports the maximum likelihood estimation of the proposed regression models on data from MM patients. The AIC and BIC in the Inverse Gaussian distribution were 66.00 and 49.32, respectively. The fitted survival curves are presented in (Figure 2).

Table 2.

Maximum Likelihood Estimates of the Fitted Models ^a

Models	$\hat{a}$	$\hat{b}$	$\hat{r}$	$\hat{u}$	$\hat{p}$	AIC	BIC
Inverse gaussian	-0.5540	1.488	1	1	0.544	72.014	59.32
Kumaraswamy inverse gaussian	-0.97	15.63	8.32	0.2	0.24	66.006	49.32

^a $p$ = Cure fraction.

Figure 2.

The fitted Kumaraswamy Inverse Gaussian model (left), the fitted inverse Gaussian model (right)

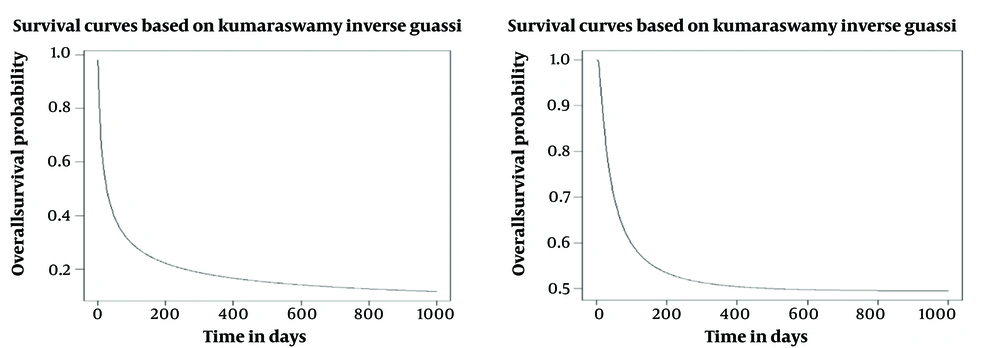
The cure fraction in the Inverse Gaussian distribution was 54.4%, while this value was 24% obtained in the Kumaraswamy Inverse Gaussian distribution. The results show that the Inverse Gaussian distribution better fits this dataset. This result was also confirmed in the study of melanoma patients by Rocha et al. (24).

The results of the univariate analysis related to the survival of MM patients using the inverse Gaussian, Kumaraswamy Inverse Gaussian model are shown in Table 3, which shows that the age of patients had a significant relationship with the overall survival (P < 0.05), which confirms the results of the previous studies (15, 33).

Table 3.

The Results of Univariate Analysis

Variables	Inverse Gaussian		P-Value	Kumaraswamy Inverse Gaussian		P-Value
Variables	AIC	BIC	P-Value	AIC	BIC	P-Value
Age	68.56	53.87	0.017 ^a	68.006	49.31	0.025 ^a
Sex	73.66	58.99	0.56	72.4	53.71	0.5
Anemia	74.016	59.32	0.074	69.66	50.97	0.07
Leukopenia	72.86	58.17	0.29	72.06	53.37	0.39
Thrombocytopenia	64.48	45.8	0.011 ^a	63.12	48.44	0.043 ^a
β2-microglobulin level	75.96	59.27	0.49	72.8	54.11	0.27
Creatinine level	74.78	58.09	0.41	71.76	53.08	0.43

^a P-value < 0.05.

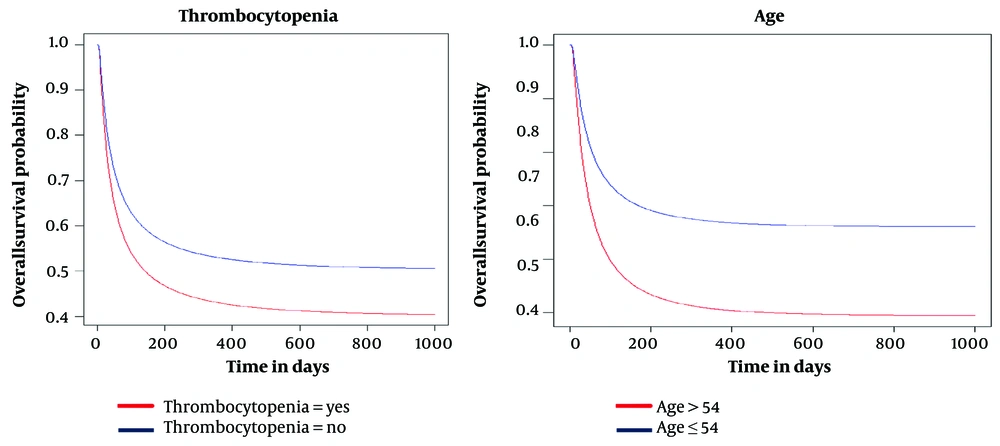
We applied the Inverse Gaussian model to the data and analyzed the age variable in two groups: Those younger than the mean age of 54 and those older than 54. The cure fraction for the group aged less than 54 was approximately 0.66, while the cure fraction for those aged 54 was 0.49. Additionally, we found a significant relationship between platelet count pre-transplant and patient survival (P < 0.05). In the Inverse Gaussian model, patients with Thrombocytopenia had a cure fraction of 0.36, indicating lower survival than those without Thrombocytopenia, which had a cure fraction of 0.54(Figure 3).

Figure 3.

The fitted Kumaraswamy inverse Gaussian model

5. Discussion

This study compared the Inverse Gaussian model with Kumaraswamy Inverse Gaussian model to accurately estimate the cure fraction and determine predictive factors in MM patients. According to goodness of fit (GOF) criteria, the Inverse Gaussian defective model was chosen as a better model to determine the predictive factors influential on the overall survival rate of MM patients and to estimate the proportion of recovered individuals (cure fraction). The results obtained in the Inverse Gaussian model were more accurate than the inverse Gaussian model of Kumaraswamy, which had a lower confidence interval for the parameters. The cure fraction in the inverse Gaussian model was 54.4%, indicating patients’ recovery rate. According to the selected model, age and Thrombocytopenia affect the survival of MM patients undergoing ASCT in this study.

Monitoring patients’ survival trends is crucial to evaluate MM treatment progress. Survival studies in various cancer types have been studied extensively (34). Appropriate models should be utilized to ensure objective and unbiased results in cancer survival studies. These models form the basis for analyzing new issues in long-term cancer survival (35). Some research studies have utilized mixture models to estimate long-term survival and the proportion of survivors (24, 36, 37). Some studies have used defective cure models to estimate the cure fraction and determine the factors affecting long-term survival time (18, 34). Defective models can estimate the cure fraction without requiring additional parameters, an advantage over previous methods. Only a few studies have utilized these models to analyze cure data. However, machine learning and artificial intelligence have been employed to identify risk factors in cancer patients, but these methods are less accurate because they do not account for treatment characteristics (38, 39). One advantage of defective models over other survival models is the inclusion of improved individuals, leading to more accurate and reliable estimates (40). In this study, we used defective cure models to identify the factors that affect overall survival in MM patients and to estimate the cure fraction. This approach offers greater flexibility, efficiency, and accuracy. According to the chosen model, pre-transplant platelet count can be used to predict the timing of transplantation and long-term survival after ASCT. A low platelet count increases the risk of death for patients, which is consistent with previous studies (41). We found that Thrombocytopenia significantly impacts the survival time of MM patients, who undergo the transplant procedure (P < 0.05). The results of a study conducted on 1,027 MM patients at the Mayo Clinic between 1985 and 1998 showed that age, plasma cell labeling index, low platelet count, serum albumin, and log creatinine values were the most important prognostic factors in MM patient survival (6). In the current study, patients who have Thrombocytopenia and experience a cure fraction of 36% tend to survive shorter than those without Thrombocytopenia, who have a cure fraction of 54%. Therefore, Thrombocytopenia can be considered one of the most influential risk factors that can influence the success of ASCT. These results are consistent with previous studies (18, 41). The study found that patients’ age significantly impacts the overall survival rate of MM patients (P < 0.05). Patients over 60 years of age have a lower chance of survival. The younger groups have a higher overall survival percentage, with a cure fraction of 66%, compared to the older groups, with a cure fraction of 49%. The study was conducted on 127 477 MM patients in Japan, and age and gender were considered risk factors in the overall survival of patients (42). Other studies have also confirmed these findings (15, 41). Although women have a higher cure fraction than men in the current study, this difference is not statistically significant. Therefore, it can be concluded that gender does not significantly affect overall survival and cure fraction. Some studies did not confirm gender significance (22), while others did (23, 43).

The article examines defective cure models that can analyze the impact of independent variables over time and offer better insights to researchers in predictive studies of long-term survival and survivor rates in various clinical fields. This paper uses the Kumaraswamy family-based cure models to analyze overall survival time and its predictive factors that build on previously published articles about the effectiveness of cure models in predicting long-term survival times (27). Although the new models used in this study did not produce results as accurate as those of the Inverse Gaussian model, this discrepancy may be due to the characteristics of the data itself. However, some studies suggest that Kumaraswamy family-based cure models provide reliable results regarding the proportion of cured individuals, their survival times, and various predictive factors in survival data (24).

The sensitivity analysis results suggest that a shorter follow-up period leads to slight inflation of the estimated cure rates based on the defective Inverse Gaussian model. These results are in tandem with previous studies on flexible cure models. Models with greater flexibility have a more significant potential for variation in estimates. Nevertheless, the model used in this study did not show great sensitivity to cohort length (26).

5.1 Limitation

The study had some limitations. Firstly, the data collection process was time-consuming because a statistical group carried it out. Secondly, the data were gathered from only one medical center; so, the findings cannot be generalized to all patients with MM. The results should be obtained through larger, multicenter studies. Furthermore, acquiring more patient information, such as their socioeconomic status and family history, would benefit the study.

5.2 Conclusions

The results show that patient age and platelet count in pre-transplant blood tests are influential factors affecting the overall survival of MM patients. Diagnosing this disease early and at a younger age can significantly increase patients’ life expectancy. The cure model application helps obtain precise estimates of cure fractions and important predictive factors impacting MM patients’ survival time. Although the models discussed in this article center on MM data, they can be valuable tools for evaluating overall survival in numerous neoplasms. Increasing the sample size and extending the follow-up time can improve the accuracy and efficiency of survival analysis, helping to identify critical predictive factors.

Acknowledgements

Footnotes

Authors' Contribution: L. J. N. and A. B. contributed to the conception, designed the evaluation, and performed parts of the statistical analysis. A. A. K. M. revised the manuscript, performed the statistical analysis, and revised the manuscript. D. K. and L. J. N. collected clinical data and interpreted and revised the manuscript. A. B. and A. A. K. M. reanalyzed the clinical and statistical data and revised the manuscript. A. A. K. M. and L. J. N. agreed to be responsible for all written parts. All authors read and approved the final manuscript.
Conflict of Interests Statement: The authors declare no conflict of interest.
Data Availability: The dataset presented in the study is available on request from the corresponding author during submission or after publication. However, due to privacy problems, the data are not publicly available.
Ethical Approval:This study is approved under the ethical approval code of IR.SBMU.RETECH.REC.1402.487 .
Funding/Support: The authors declared that they have no funding/support.
Informed Consent: Informed consent was obtained from all patients.

References

1.
Li J, Zhu Y. Survival analysis of multiple myeloma patients after autologous stem cell transplantation. Stem Cell Investig. 2019;6:42. [PubMed ID: 32039264]. [PubMed Central ID: PMC6987323]. https://doi.org/10.21037/sci.2019.10.05.
2.
Gerecke C, Fuhrmann S, Strifler S, Schmidt-Hieber M, Einsele H, Knop S. The diagnosis and treatment of multiple myeloma. Dtsch Arztebl Int. 2016;113(27-28):470-6. [PubMed ID: 27476706]. [PubMed Central ID: PMC4973001]. https://doi.org/10.3238/arztebl.2016.0470.
3.
Ferlay JE, Lam F, Laversanne M, Colombet M, Mery L, Piñeros M, et al. Global cancer observatory: Cancer today. Lyon, France: Int Agency Res Cancer; 2024. Available from: https://gco.iarc.who.int/media/globocan/factsheets/cancers/35-multiple-myeloma-fact-sheet.pdf.
4.
National Cancer Institute. All cancer sites combined recent trends in SEER age-adjusted incidence rates, 2000-2021. 2024. Available from: https://seer.cancer.gov/statistics-network/explorer/application.html?site=1&data_type=1&graph_type=2&compareBy=sex&chk_sex_3=3&chk_sex_2=2&rate_type=2&race=1&age_range=1&hdn_stage=101&advopt_precision=1&advopt_show_ci=on&hdn_view=0&advopt_show_apc=on&advopt_display=2#resultsRegion0.
5.
Landgren O, Weiss BM. Patterns of monoclonal gammopathy of undetermined significance and multiple myeloma in various ethnic/racial groups: Support for genetic factors in pathogenesis. Leukemia. 2009;23(10):1691-7. [PubMed ID: 19587704]. https://doi.org/10.1038/leu.2009.134.
6.
Kyle RA, Gertz MA, Witzig TE, Lust JA, Lacy MQ, Dispenzieri A, et al. Review of 1027 patients with newly diagnosed multiple myeloma. Mayo Clin Proc. 2003;78(1):21-33. [PubMed ID: 12528874]. https://doi.org/10.4065/78.1.21.
7.
Rajkumar SV. Updated diagnostic criteria and staging system for multiple myeloma. Am Soc Clin Oncol Educ Book. 2016;35:e418-23. [PubMed ID: 27249749]. https://doi.org/10.1200/EDBK_159009.
8.
Landgren O, Kyle RA, Pfeiffer RM, Katzmann JA, Caporaso NE, Hayes RB, et al. Monoclonal gammopathy of undetermined significance (MGUS) consistently precedes multiple myeloma: A prospective study. Blood. 2009;113(22):5412-7. [PubMed ID: 19179464]. [PubMed Central ID: PMC2689042]. https://doi.org/10.1182/blood-2008-12-194241.
9.
Weiss BM, Abadie J, Verma P, Howard RS, Kuehl WM. A monoclonal gammopathy precedes multiple myeloma in most patients. Blood. 2009;113(22):5418-22. [PubMed ID: 19234139]. [PubMed Central ID: PMC2689043]. https://doi.org/10.1182/blood-2008-12-195008.
10.
Smith A, Wisloff F, Samson D, U. K. Myeloma Forum, Nordic Myeloma Study G, British Committee for Standards in H. Guidelines on the diagnosis and management of multiple myeloma 2005. Br J Haematol. 2006;132(4):410-51. [PubMed ID: 16412016]. https://doi.org/10.1111/j.1365-2141.2005.05867.x.
11.
Brautigam M, Biskup E. [CME: Multiple myeloma - a review]. Praxis (Bern 1994). 2018;107(14):749-54. [PubMed ID: 29969971]. https://doi.org/10.1024/1661-8157/a002984.
12.
Terpos E, Kleber M, Engelhardt M, Zweegman S, Gay F, Kastritis E, et al. European Myeloma Network guidelines for the management of multiple myeloma-related complications. Haematologica. 2015;100(10):1254-66. [PubMed ID: 26432383]. [PubMed Central ID: PMC4591757]. https://doi.org/10.3324/haematol.2014.117176.
13.
Wallington-Beddoe CT, Mynott RL. Prognostic and predictive biomarker developments in multiple myeloma. J Hematol Oncol. 2021;14(1):151. [PubMed ID: 34556161]. [PubMed Central ID: PMC8461914]. https://doi.org/10.1186/s13045-021-01162-7.
14.
Weinhold N, Ashby C, Rasche L, Chavan SS, Stein C, Stephens OW, et al. Clonal selection and double-hit events involving tumor suppressor genes underlie relapse in myeloma. Blood. 2016;128(13):1735-44. [PubMed ID: 27516441]. [PubMed Central ID: PMC5043128]. https://doi.org/10.1182/blood-2016-06-723007.
15.
Bringhen S, Mateos MV, Zweegman S, Larocca A, Falcone AP, Oriol A, et al. Age and organ damage correlate with poor survival in myeloma patients: Meta-analysis of 1435 individual patient data from 4 randomized trials. Haematologica. 2013;98(6):980-7. [PubMed ID: 23445873]. [PubMed Central ID: PMC3669456]. https://doi.org/10.3324/haematol.2012.075051.
16.
Attal M, Harousseau JL, Stoppa AM, Sotto JJ, Fuzibet JG, Rossi JF, et al. A prospective, randomized trial of autologous bone marrow transplantation and chemotherapy in multiple myeloma. Intergroupe Francais du Myelome. N Engl J Med. 1996;335(2):91-7. [PubMed ID: 8649495]. https://doi.org/10.1056/NEJM199607113350204.
17.
Child JA, Morgan GJ, Davies FE, Owen RG, Bell SE, Hawkins K, et al. High-dose chemotherapy with hematopoietic stem-cell rescue for multiple myeloma. N Engl J Med. 2003;348(19):1875-83. [PubMed ID: 12736280]. https://doi.org/10.1056/NEJMoa022340.
18.
Kadkhoda D, Nikoonezhad M, Bonakchi H, Mehdizadeh M, Hajifathali A, Baghestani AR, et al. Investigating the effect of pre-transplant thrombocytopenia and anemia on the engraftment and long-term survival in multiple myeloma patients. Transpl Immunol. 2024;82:101991. [PubMed ID: 38199269]. https://doi.org/10.1016/j.trim.2024.101991.
19.
Bertrand A, Legrand C, Léonard D, Van Keilegom I. Robustness of estimation methods in a survival cure model with mismeasured covariates. Comput Stat Data Anal. 2017;113:3-18. https://doi.org/10.1016/j.csda.2016.11.013.
20.
Ghitany ME, Maller R, Zhou S. Estimating the proportion of immunes in censored samples: A simulation study. Stat Med. 1995;14(1):39-49. [PubMed ID: 7701157]. https://doi.org/10.1002/sim.4780140106.
21.
Arano I, Sugimoto T, Hamasaki T, Ohno Y. Practical application of cure mixture model for long-term censored survivor data from a withdrawal clinical trial of patients with major depressive disorder. BMC Med Res Methodol. 2010;10:33. [PubMed ID: 20412598]. [PubMed Central ID: PMC2880122]. https://doi.org/10.1186/1471-2288-10-33.
22.
Chen M, Ibrahim JG, Sinha D. A New Bayesian Model for Survival Data with a Surviving Fraction. J Am Stat Assoc. 1999;94(447). https://doi.org/10.1080/01621459.1999.10474196.
23.
Balka J, Desmond AF, McNicholas PD. Bayesian and likelihood inference for cure rates based on defective inverse Gaussian regression models. J Appl Stat. 2011;38(1):127-44. https://doi.org/10.1080/02664760903301127.
24.
Rocha R, Nadarajah S, Tomazella V, Louzada F, Eudes A. New defective models based on the Kumaraswamy family of distributions with application to cancer data sets. Stat Methods Med Res. 2017;26(4):1737-55. [PubMed ID: 26092478]. https://doi.org/10.1177/0962280215587976.
25.
Rajkumar SV. Treatment of multiple myeloma. Nat Rev Clin Oncol. 2011;8(8):479-91. [PubMed ID: 21522124]. [PubMed Central ID: PMC3773461]. https://doi.org/10.1038/nrclinonc.2011.63.
26.
Evans RS, Duane RT. Acquired hemolytic anemia; the relation of erythrocyte antibody production to activity of the disease; the significance of thrombocytopenia and leukopenia. Blood. 1949;4(11):1196-213. [PubMed ID: 18143402].
27.
Jabari Nanva L, Baghestani AR, Khadem Maboudi AA, Kadkhoda D. Long-term survival of multiple myeloma patients using cure models. Arch Advances Biosci. 2024;15(1):1-8. https://doi.org/10.22037/aab.v15i1.43103.
28.
Balka J, Desmond AF, McNicholas PD. Review and implementation of cure models based on first hitting times for Wiener processes. Lifetime Data Anal. 2009;15(2):147-76. [PubMed ID: 19123058]. https://doi.org/10.1007/s10985-008-9108-y.
29.
Denault WRP, Jugessur A. Detecting differentially methylated regions using a fast wavelet-based approach to functional association analysis. BMC Bioinformatics. 2021;22(1):61. [PubMed ID: 33568045]. [PubMed Central ID: PMC7876806]. https://doi.org/10.1186/s12859-021-03979-y.
30.
Cantor AB, Shuster JJ. Parametric versus non-parametric methods for estimating cure rates based on censored survival data. Stat Med. 1992;11(7):931-7. [PubMed ID: 1604072]. https://doi.org/10.1002/sim.4780110710.
31.
Cordeiro GM, de Castro M. A new family of generalized distributions. J Stat Comput Simul. 2011;81(7):883-98. https://doi.org/10.1080/00949650903530745.
32.
R Core Team. A language and environment for statistical computing, R Foundation for statistical computing. Open J Statist. 2022;13(2).
33.
Kumar SK, Dispenzieri A, Lacy MQ, Gertz MA, Buadi FK, Pandey S, et al. Continued improvement in survival in multiple myeloma: Changes in early mortality and outcomes in older patients. Leukemia. 2014;28(5):1122-8. [PubMed ID: 24157580]. [PubMed Central ID: PMC4000285]. https://doi.org/10.1038/leu.2013.313.
34.
Kadkhoda D, Baghestani AR, Parkhideh S, Bonakchi H, Khadem MA. Comparison of the cure rate in blood cancer patients using defective marshall-olkin extended weibull model. Iran Red Crescent Med J. 2023;25(12). e2119. https://doi.org/10.32592/ircmj.2023.25.12.2119.
35.
Othus M, Barlogie B, Leblanc ML, Crowley JJ. Cure models as a useful statistical tool for analyzing survival. Clin Cancer Res. 2012;18(14):3731-6. [PubMed ID: 22675175]. [PubMed Central ID: PMC3744099]. https://doi.org/10.1158/1078-0432.CCR-11-2859.
36.
Calsavara VF, Rodrigues AS, Rocha R, Tomazella V, Louzada F. Defective regression models for cure rate modeling with interval-censored data. Biom J. 2019;61(4):841-59. [PubMed ID: 30868619]. https://doi.org/10.1002/bimj.201800056.
37.
Usmani SZ, Hoering A, Cavo M, Miguel JS, Goldschimdt H, Hajek R, et al. Clinical predictors of long-term survival in newly diagnosed transplant eligible multiple myeloma-an IMWG Research Project. Blood Cancer J. 2018;8(12):123. [PubMed ID: 30470751]. [PubMed Central ID: PMC6251924]. https://doi.org/10.1038/s41408-018-0155-7.
38.
Arya N, Saha S. Multi-modal advanced deep learning architectures for breast cancer survival prediction. Knowledge-Based Systems. 2021;221. https://doi.org/10.1016/j.knosys.2021.106965.
39.
Vanneschi L, Farinaccio A, Mauri G, Antoniotti M, Provero P, Giacobini M. A comparison of machine learning techniques for survival prediction in breast cancer. BioData Min. 2011;4:12. [PubMed ID: 21569330]. [PubMed Central ID: PMC3108919]. https://doi.org/10.1186/1756-0381-4-12.
40.
Botta L, Gatta G, Capocaccia R, Stiller C, Canete A, Dal Maso L, et al. Long-term survival and cure fraction estimates for childhood cancer in Europe (EUROCARE-6): results from a population-based study. Lancet Oncol. 2022;23(12):1525-36. [PubMed ID: 36400102]. https://doi.org/10.1016/S1470-2045(22)00637-4.
41.
Merchionne F, Procaccio P, Dammacco F. Long-term survival in multiple myeloma: A single-center experience. Clin Exp Med. 2008;8(3):133-9. [PubMed ID: 18791685]. https://doi.org/10.1007/s10238-008-0169-8.
42.
Khan MM, Mori M, Sakauchi F, Matsuo K, Ozasa K, Tamakoshi A, et al. Risk factors for multiple myeloma: Evidence from the Japan Collaborative Cohort (JACC) study. Asian Pac J Cancer Prev. 2006;7(4):575-81. [PubMed ID: 17250430].
43.
Derman BA, Langerman SS, Maric M, Jakubowiak A, Zhang W, Chiu BC. Sex differences in outcomes in multiple myeloma. Br J Haematol. 2021;192(3):e66-9. [PubMed ID: 33216365]. [PubMed Central ID: PMC8182969]. https://doi.org/10.1111/bjh.17237.

comments

Pre-transplant Predictive Factors in Multiple Myeloma Patients Undergoing Autologous Stem Cell Transplantation Using Defective Cure Models

Abstract

Background:

Objectives:

Methods:

Results:

Conclusions:

Keywords

1. Background

2. Objectives

3. Methods

3.1. Participants and Procedures

3.2. Statistical Analysis

4. Results

Patient Characteristics

Kaplan-Meier of overall survival

Maximum Likelihood Estimates of the Fitted Models a

The fitted Kumaraswamy Inverse Gaussian model (left), the fitted inverse Gaussian model (right)

The Results of Univariate Analysis

The fitted Kumaraswamy inverse Gaussian model

5. Discussion

5.1 Limitation

5.2 Conclusions

Acknowledgements

References

Cookie Setting

Maximum Likelihood Estimates of the Fitted Models ^a