Abstract
Background:
Rapid progression in medical and health sciences have caused survival studies, where some patients have long-term survival, especially for chronic diseases such as breast cancer. Cure models can be applicable to analyze such data.Objectives:
The aim of this study was to determine the risk factors associated with breast cancer, using mixture cure fraction model.Methods:
We studied data for 438 patients, who were referred to cancer research center in Shahid Beheshti University of Medical Sciences. The patients were visited and treated during 1992 to 2012 and followed-up until October 2014. The data were analyzed by mixture cure fraction model based on GMW (generalized modified Weibull) distribution and inferences were obtained with Bayesian approach, using standard MCMC (Markov Chain Monte Carlo) methods. All analyses were performed, using SPSS v20 and OpenBUGS software. The significant level was considered at 0.05.Results:
During the follow-up period, 75 (17.12%) deaths occurred by breast cancer and the one-year overall survival rate was 98%. Covariates such as numbers of metastatic lymph nodes and histologic grade were statistically significant. Also, the cure fraction estimation was obtained 58%.Conclusions:
When some patients have a long-term survival, cure models can be an interesting model to study survival and these models estimate parameters better than the traditional models such as cox model. In this paper, the mixture cure fraction model based on GMW was fitted for analysing survival times in patients with breast cancer.Keywords
1. Background
One of the major causes of death and disability among women in developed countries and in some developing countries is breast cancer (1-3). Overall, 1.67 million patients and 0.52 million deaths all around the world are recorded by breast cancer (4, 5). In Iran, the first cause of death among women is breast cancer with diagnosed age between 40 to 49 years (6). The prognostic factors of breast cancer can be grouped in two categories: chronological and biological (7). The first and the second categories are based on the amount of time present and the behavior of tumor, respectively. Lymph node status and tumor size are time-dependent factors, but histological grade is a biological factor (8). However, the effects of factors such as age at diagnosis, stage of cancer, the prescribed chemotherapy agent, lymph node status, tumor size, histological grade, hormonal factors, and family history are unclear and challenging issues (9, 10). Also in breast cancer, we now encounter a heterogeneous population of patients. Patients are categorized into two groups. One group never experience the event of interest, so they are not at risk (11). These patients are considered cured or immunized. The second group contains patients who remain uncured. However, one of the goals in survival analysis is to estimate the proportion of cured patients. Two types of cure fraction models are the mixture and non-mixture (12). Du to recent developments in treatment and considerable proportion of cured patients, more attention has been paid to cancer-relapse trials, including breast cancer, leukaemia, prostate cancer, melanoma, head, and neck cancer (13).
The Kaplan-Meier estimators, log-rank test, or semi-parametric models including Cox proportional hazards, as a standard survival analysis method, provide no direct estimate of the cure fraction (14). The Weibull is one of the common and applicable distributions in cancer studies (15), because of simple estimation of parameters and its hazard function capability. In survival analysis studies, however, we usually have data sets that need more complex parametric models. So, a new class of parametric distributions based on extensions of the Weibull distribution is generalized modified Weibull (GMW). It was introduced by Carrasco in 2008 (16) and developed in the form of mixture and non- mixture cure fraction models by Martinez in 2013 to analyze the survival data in presence of cure fraction, censored data, and covariate with Bayesian approach.
The present study aims at applying mixture cure fraction model, based on the generalized modified Weibull distribution and including covariate to assess the association between possible risk factors and prognostic factors that may affect the survival of patients with breast cancer.
2. Methods
2.1. Patients and Variables Under Study
The present retrospective study was performed in 438 women with breast cancer, who were referred to cancer research center in Shahid Beheshti University of Medical Sciences, Tehran, Iran with ethical code SBMU.REC.1393.587. The patients were visited and treated during 1992 to 2012 and followed-up until October 2014. The status of the patients (i.e. whether they were still alive or not) was assessed, using the registered phone number in the health files of the patients. The longest duration of follow-up was 253 months. A total of 75 patients (17.08%) experienced the interest event and 363 patients were censored. For each of the 438 patients in this database, we studied prognostic variables such as age at diagnosis, family history of cancer, abortion, breastfeeding, marital status, tumor size, estrogen and progesterone receptor status, type of surgery (modified radical mastectomy or breast conserving surgery), histologic and nuclear grading, axillary lymph node status (N0, N1, N2 and N3 category), lymphovascular invasion and, stage of disease. These were included in the model, using binary variables. We defined survival time between the first diagnosis of breast cancer and death or the end of patient follow-up. A binary censoring variable was used to indicate whether a patient died of breast cancer. The protocol of the current study was confirmed by the ethical committee of Shahid Beheshti University of Medical Sciences. The data were analyzed by SPSS v20 and OpenBUGS software. The significant level was considered at 0.05.
2.2. Statistical Analysis
2.2.1. Mixture Cure Fraction Models
Following Maller and Zhou (17), mixture cure fraction models are:
S(t) = p + (1 - p)S0 (t)
Where p represents the proportion of “long-term survivors” or “cured patients” (0| < P| < |1) and S0(t) is the baseline survival function for the susceptible individuals. The probability density function for the lifetime T is:
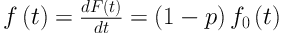
Where f(t)= 1 - S(t) and f0 (t) is the baseline probability density function for the susceptible individuals. Considering a random sample (ti, δi) of size n, i| = 1|, …, n, the contribution of the ith subject for the likelihood function is given by:
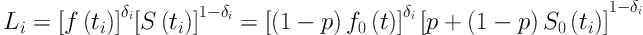
Where δi is an indicator variable for censoring, that is, δi| = |1 for an event and δi| = |0 for a censored.
2.2.2. Parametric Distribution
2.2.2.1. The Generalized Modified Weibull Distribution
There are various distributions to select; here we assume the generalized modified Weibull (GMW) distribution for the mixture cure fraction model. The probability density function for the GMW distribution is:
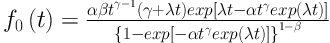
This four-parameter distribution was introduced by Carrasco et al. (16). This distribution is applicable to consider many shapes of the hazard function such as bathtub-shaped failure rates data. The importance of this distribution stands in its capability to model both monotone and non-monotone failure rates.
The respective survival function is can be written as:
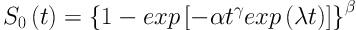
The GMW distribution is denoted by X| ∼ |GMW (α, β, γ, λ).
We also assume that vector of covariates xi could be included to model by parameter p:
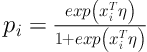
Where η is a vector of unknown parameters.
2.2.3. Bayesian Inference
The joint posterior distribution for the parameters could be obtained, using Bayes theorem by jointing the prior distribution with the likelihood function for θ. Due to the joint posterior distribution of the proposed model is computationally complex, MCMC (Markov Chain Monte Carlo) simulation methods can be used to generate samples of the joint posterior distribution. OpenBUGS software is used to simulate these samples with specifying the distribution for the data and the prior distributions for the parameters. For a Bayesian analysis of the mixture model with covariates, approximately non-informative priors such as Gamma (1, 1) prior distributions for the parameters α, β, γ and λ and also normal prior distributions N(0, 100) for the parameters ηi were assumed. In this paper, for eliminating the effect of the initial values, a ‘burn-period’ size of 1000 was used; after this ‘burn-in-sample’ period, 100,000 Gibbs Samples were generated, taking every 100th sample. Convergence of the algorithm was assessed, using standard methods as the trace-plots of the simulated samples.
3. Results
3.1. Patient Characteristics
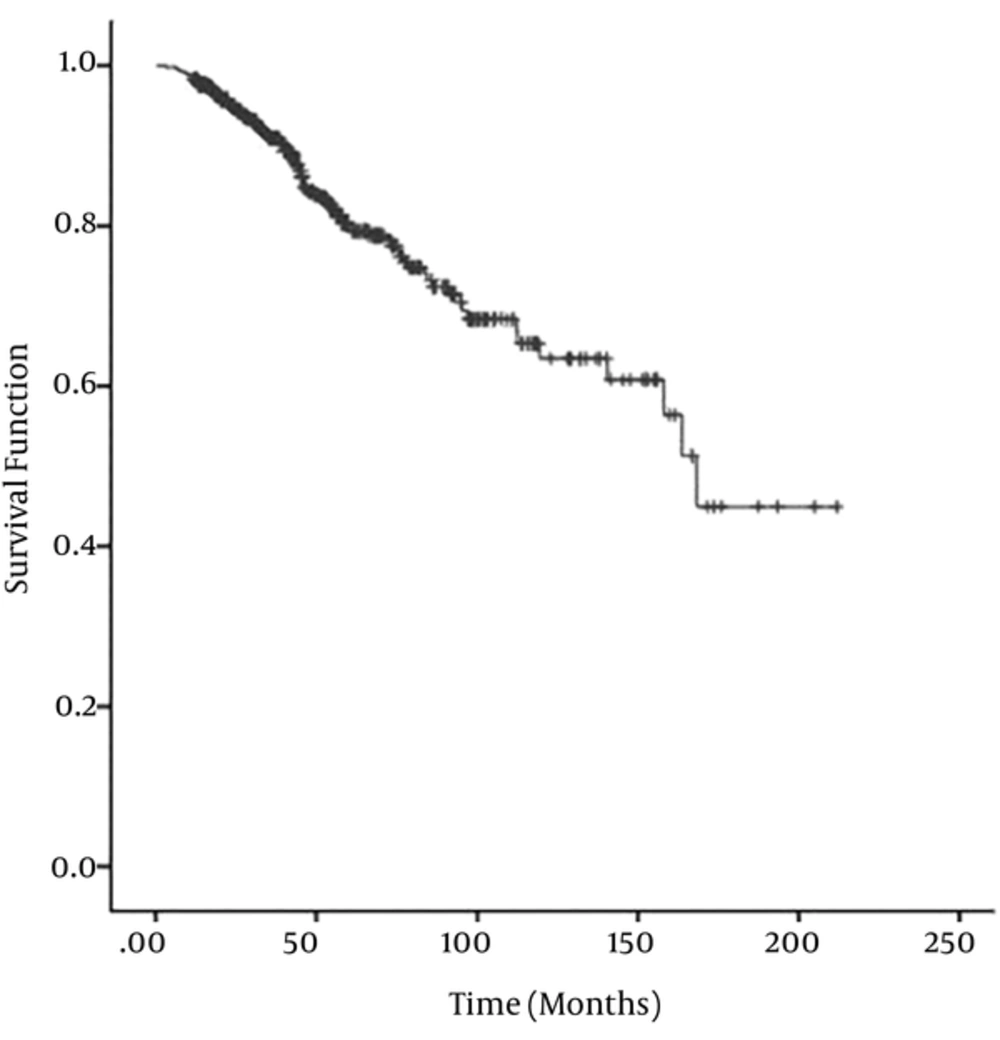
The clinical, pathological, and biological characteristics of the 438 women with breast cancer were presented in Table 1. The mean age at the time of diagnosis was 48.37 ± 10.92 with the range of 22 to 40 years. The mean duration of follow-up was 52.3 with the range of 3 to 253 months. During the study up to October 2014, 75 (17.12%) deaths caused by breast cancer were recorded. With respect to the life-table method, the one-year overall survival rate was 98% (95% CI: 97% - 99%). The Kaplan–Meier estimate of the survival function for the breast cancer data was illustrated in, Figure 1 where the presence of a plateau near to 0.5 observed in the graph suggests that models that ignore the proportion p will not be appropriate, so more accurate results were obtained, using the cure fraction model.
Patients’ Characteristics
| Survived (n = 363) | Deceased (n = 75) | Total (n = 438) | |
|---|---|---|---|
| Surgery | |||
| BCS | 253 (92.3) | 21 (7.7) | 272 (100) |
| MRM | 110 (67.1) | 54 (32.9) | 164 (100) |
| Stage | |||
| I | 92 (95.8) | 4 (4.2) | 96 (100) |
| II | 175 (90.7) | 18 (9.3) | 193 (100) |
| III | 91 (67.4) | 44 (32.6) | 135 (100) |
| IV | 5 (35.7) | 9 (64.3) | 14 (100) |
| Grade | |||
| I | 46 (97.9) | 1 (2.1) | 47 (100) |
| II | 211 (89.8) | 24 (10.2) | 235 (100) |
| III | 106 (67.9) | 50 (32.1) | 156 (100) |
| Lymphovascular Invasion (LVI) | |||
| Negative | 241 (90.6) | 25 (9.4) | 266 (100) |
| Positive | 122 (70.9) | 50 (29.1) | 172(100) |
| Estrogen receptor | |||
| Negative | 95 (75.4) | 31 (24.6) | 126 (100) |
| Positive | 268 (85.9) | 44 (14.1) | 312 (100) |
| Progesterone receptor | |||
| Negative | 114 (76) | 36 (24) | 150 (100) |
| Positive | 249 (86.5) | 39 (13.5) | 288 (100) |
| Tumor Size | |||
| < 2 | 103 (92.8) | 8 (7.2) | 111 (100) |
| 2 - 5 | 208 (86) | 34 (14) | 242 (100) |
| ≥ 5 | 52 (61.2) | 33 (38.8) | 85 (100) |
| Lymph node status | |||
| N0 | 188 (94.9) | 10 (5.1) | 198 (100) |
| N1 | 105 (86.8) | 16 (13.2) | 121 (100) |
| N3 | 27 (69.2) | 12 (30.8) | 39 (100) |
| N4 | 43 (53.8) | 37 (46.2) | 80 (100) |
| Abortion | |||
| Yes | 121 (82.1) | 22 (17.9) | 143 (100) |
| No | 220 (82.2) | 31 (17.8) | 251 (100) |
| Family history of cancer | |||
| Yes | 106 (85.5) | 18 (14.5) | 124 (100) |
| No | 257 (81.8) | 57 (18.2) | 314 (100) |
| Marital status | |||
| Single | 22 (91.7) | 2 (8.3) | 24 (100) |
| Married | 341 (82.4) | 73 (17.6) | 414 (100) |
| Breastfeeding | |||
| Yes | 296 (77.7) | 51 (13.3) | 347 (100) |
| No | 45 (89.5) | 2 (10.5) | 47 (100) |
| Age at diagnosis | |||
| < 40 | 63 (71.6) | 25 (28.4) | 88 (100) |
| 40 - 70 | 289 (86) | 47 (14) | 336 (100) |
| ≥ 70 | 11 (78.6) | 3 (21.4) | 14 (100) |
Kaplan-Meier estimate of the overall survival function for the breast cancer data
The covariates included in the model via logit link that were explained in statistical analysis section. These variables under study were age at diagnosis, marital status, history of abortion, history of breastfeeding, family history of breast cancer, type of surgery, number of metastatic lymph nodes, tumor size, stage, histologic grade, estrogen receptor, progesterone receptor, and lymphovascular invasion. Results are shown in Table 2. The percent credible intervals for the two prognostic variables such as number of metastatic lymph nodes and histologic grade contained zero, meaning that they are statistically significant. Indeed, patients with histologic grade I were 5.26 times more at the risk of death compared to patients with histologic grade III. In addition, cure fraction was estimated 58%.
Posterior Estimates Using the Mixture Model Based on GMW Distribution
| Prognostic Variables | Posteriora | 95% Credible Interval | OR |
|---|---|---|---|
| Surgery | |||
| BCS | -0.042 (0.085) | (-0.21 - 0.12 ) | 0.95 |
| MRM | Reference | ||
| Stage | |||
| I | 0.071 (0.098) | (-0.11 - 0.26) | 1.07 |
| II | 0.102 (0.097) | (-0.08 - 0.29) | 1.11 |
| III | -0.107 (0.095) | (-0.3 - 0.07) | 0.89 |
| IV | Reference | ||
| Grade | |||
| I | 1.661 (1.051) | (1.33 - 2.61) | 5.26b |
| II | 2.036 (1.682) | (1.89 - 2.98) | 7.65b |
| III | Reference | ||
| Lymphovascular Invasion (LVI) | |||
| Negative | -0.128 (0.093) | (-0.31 - 0.05) | 0.88 |
| Positive | Reference | ||
| Estrogen Receptor | |||
| Positive | 0.062 (0.096) | (-0.12 - 0.25) | 1.06 |
| Negative | Reference | ||
| Progesterone receptor | |||
| Negative | 0.068 (0.095) | (-0.11 - 0.26) | 1.07 |
| Positive | Reference | ||
| Tumor Size | |||
| < 2 | 0.058 (0.097) | (-0.12 - 0.24) | 1.05 |
| 2 - 5 | 0.051 (0.093) | (-0.13 - 0.23) | 1.05 |
| ≥ 5 | Reference | ||
| Lymph node status | |||
| N0 | 1.153 (0.941) | (0.81 - 2.23) | 3.16b |
| N1 | 1.782 (1.035) | (1.21 - 2.51) | 5.94b |
| N3 | 1.891 (1.314) | (1.23 - 2.66) | 6.62b |
| N4 | Reference | ||
| Abortion | |||
| Yes | -0.006 (0.094) | (-0.19 - 0.17) | 0.99 |
| No | 1 | ||
| Family history of cancer | |||
| Yes | 0.026 (0.095) | (-0.16 - 0.21) | 1.02 |
| No | Reference | ||
| Marital status | |||
| Single | 0.012 (0.095) | (-0.17 - 0.2) | 1.01 |
| Married | Reference | ||
| Breastfeeding | |||
| Yes | 0.003 (0.096) | (-0.18 - 0.19) | 1.00 |
| No | Reference | ||
| Age at diagnosis | |||
| < 40 | -0.036 (0.095) | (-0.22- 0.15) | 0.96 |
| 40 - 70 | 0.073 (0.096) | (-0.11 - 0.26) | 1.07 |
| ≥ 70 | Reference |
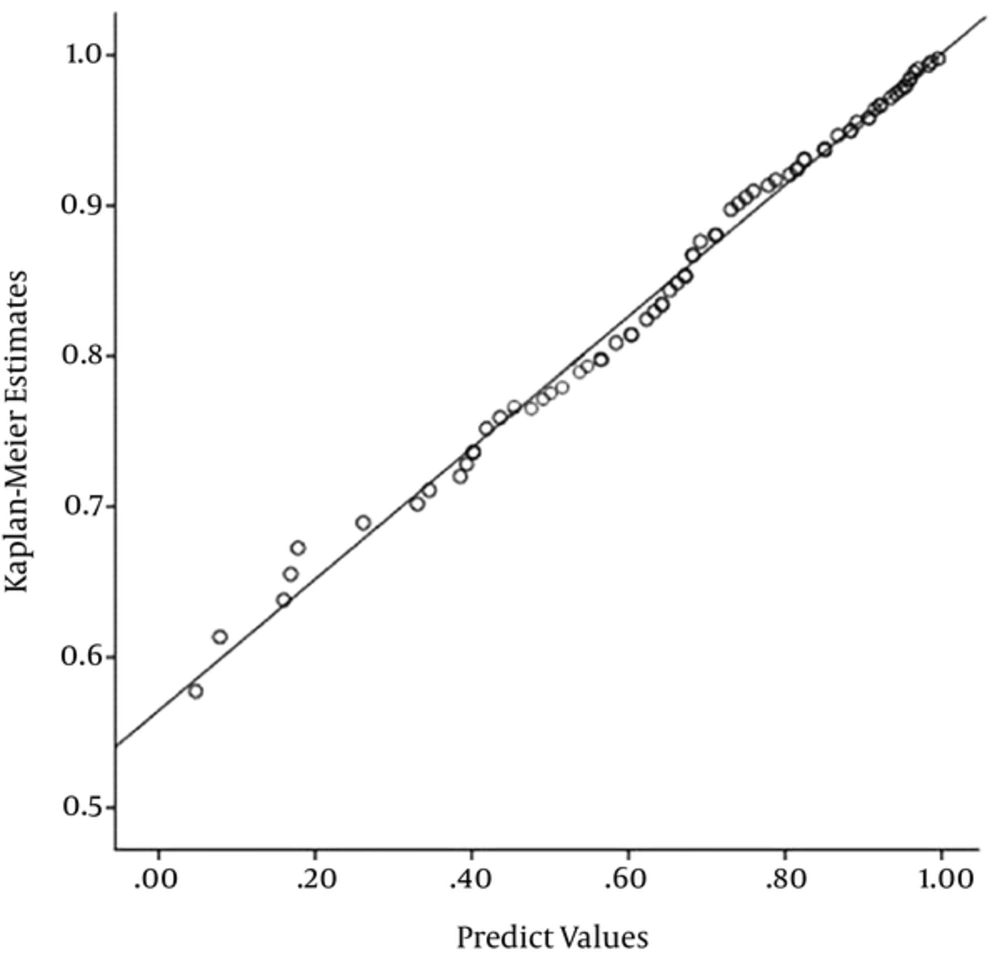
For more visual representation of the model fit, the Kaplan-Meier estimates for the survival function against the respective predicted values from the GMW mixture model were presented. With respect to Figure 2, the predicted values obtained from the fitted model are close to the empirical values, suggesting that this model is suitable for data under study.
Plots of the Kaplan-Meier estimates for the survival function versus the respective predicted values obtained from the GMW mixture models. The diagonal straight lines represent a perfect agreement between Kaplan–Meier estimates and predicted values.
4. Discussion
In this study, the mixture cure fraction model based on GMW was used. The results showed that the mentioned model was fitted to patients with breast cancer well.
In the last few decades, monitoring trends in survival of patients over time is one of the suitable ways to asses progression in the treatment of cancer (18). Treatments for many types of cancers have been improved impressively; so, we face an increase in the proportion of patients who cured (19). The proportion of such patients is named cure fraction. In addition, the survival analysis by considering cure fraction is called cure rate or long-term survival models, and they play an important role in survival analysis (20). The conventional and most common method such as the Cox proportional hazards model for analyzing survival time data is not appropriate in medical research because of its assumption about proportionality of hazards (21, 22). In addition, the standard Cox model usually does not consider the cured fraction of patients that are common in many medical investigations. Several extensions of the Cox model that consider cured fraction have been argued in different studies (23-25), but these methods are not appropriate for the investigation of non-proportional hazard functions. Thus, parametric models that include a cure fraction are appropriate for analyzing such data since these models do not need proportional hazards assumption, and they are easily interpreted by physicians. Most of the survival studies using Log-rank test and Cox analysis investigated the affecting factors on the survival of patients with breast cancer.
In recent years, cure rate models have been studied in several studies and they have been well developed in the statistical research (26-31). Mixture and non-mixture are two general types of cure models. Based on the data, the mixture cure rate or non-mixture cure rate models may fit well (28).
The aim of the current study was to investigate the relationship between survival of patients with breast cancer and associated risk factor, using mixture cure fraction model based on GMW distribution. The results showed a cure fraction model is suitable for modelling breast cancer data. Based on the findings of this study, lymph node status and histologic grade were significant as observed in other studies (32-34), but they are not in common with some studies (34-36). Histological grade that is biological was highly correlated with long-term survival. Also, this factor was reported in several studies as an important prognosis factor (4, 34).
In the current research, the mean age was about 48 years at the time of diagnosis, which is identical to Ziaei et al. study (37), while this mean is not consistent with other Iranian reports (38-43). According to the present study, the one-year overall survival rate was estimated 98%, while Movahedi’s study obtained this rate fewer than this rate (43).
In this investigation, there are some limitations. The presence of missing data on some clinical and pathological characteristics of patients, so larger sample size can reduce the problems of convergence and model fit (44). In addition to chronological and biological factors, one of the major factors that takes part in the transition of global cancer epidemiology is urbanization (45); hence, we suggest to investigate the relationship between the urbanization factor and incidence of breast cancer, using cure models in the future studies. Also, conducting further studies by assuming other generalized distributions such as the generalized F distribution (46) and the extended family of the generalized Gamma distribution (47) rather than GMW for lifetime are recommended.
5. Conclusions
Cure models could be useful for a wide range of cancers such as head and neck, colon cancer, stomach, breast, etc. However, when some patients are the long-term survivors, cure models can be beneficial methods to study survival. In addition, GMW distribution is a flexible tool for parametric survival analysis. In this paper, we concluded that the mixture cure fraction model based on GMW was suitable for survival analysis of the patients with breast cancer.
Acknowledgements
References
-
1.
Garcia-Laencina PJ, Abreu PH, Abreu MH, Afonoso N. Missing data imputation on the 5-year survival prediction of breast cancer patients with unknown discrete values. Comput Biol Med. 2015;59:125-33. [PubMed ID: 25725446]. https://doi.org/10.1016/j.compbiomed.2015.02.006.
-
2.
Grau AM, Ata A, Foster L, Ahmed NU, Gorman DR, Shyr Y, et al. Effect of race on long-term survival of breast cancer patients: transinstitutional analysis from an inner city hospital and university medical center. Am Surg. 2005;71(2):164-70. [PubMed ID: 16022018].
-
3.
Foo CS, Su D, Chong CK, Chng HC, Tay KH, Low SC, et al. Breast cancer in young Asian women: study on survival. ANZ J Surg. 2005;75(7):566-72. [PubMed ID: 15972049]. https://doi.org/10.1111/j.1445-2197.2005.03431.x.
-
4.
Baghestani AR, Moghaddam SS, Majd HA, Akbari ME, Nafissi N, Gohari K. Application of a Non-Mixture Cure Rate Model for Analyzing Survival of Patients with Breast Cancer. Asian Pac J Cancer Prev. 2015;16(16):7359-63. [PubMed ID: 26514537].
-
5.
Momenyan S, Baghestani AR, Momenyan N, Naseri P, et al. Survival prediction of patients with breast cancer: comparisons of decision tree and logistic regression analysis. Int J Cancer Manag. 2018. Forthcoming. e9176.
-
6.
Haghshenas MR, Mousavi T, Moosazadeh M, Afshari M. Human papillomavirus and breast cancer in Iran: a meta- analysis. Iran J Basic Med Sci. 2016;19(3):231-7. [PubMed ID: 27114791]. [PubMed Central ID: PMC4834111].
-
7.
Bundred NJ. Prognostic and predictive factors in breast cancer. Cancer Treat Rev. 2001;27(3):137-42. [PubMed ID: 11417963]. https://doi.org/10.1053/ctrv.2000.0207.
-
8.
Ture M, Tokatli F, Kurt I. Using Kaplan–Meier analysis together with decision tree methods (C&RT, CHAID, QUEST, C4.5 and ID3) in determining recurrence-free survival of breast cancer patients. Expert Systems Appl. 2009;36(2):2017-26. https://doi.org/10.1016/j.eswa.2007.12.002.
-
9.
Davoodi SH, Malek-Shahabi T, Malekshahi-Moghadam A, Shahbazi R, Esmaeili S. Obesity as an important risk factor for certain types of cancer. Iran J Cancer Prev. 2013;6(4):186-94. [PubMed ID: 25250133]. [PubMed Central ID: PMC4142931].
-
10.
Delen D, Walker G, Kadam A. Predicting breast cancer survivability: a comparison of three data mining methods. Artif Intell Med. 2005;34(2):113-27. [PubMed ID: 15894176]. https://doi.org/10.1016/j.artmed.2004.07.002.
-
11.
Lambert PC. Modeling of the cure fraction in survival studies. Stata J. 2007;7(3):351.
-
12.
Lambert PC, Thompson JR, Weston CL, Dickman PW. Estimating and modeling the cure fraction in population-based cancer survival analysis. Biostatistics. 2007;8(3):576-94. [PubMed ID: 17021277]. https://doi.org/10.1093/biostatistics/kxl030.
-
13.
Gu Y, Sinha D, Banerjee S. Analysis of cure rate survival data under proportional odds model. Lifetime Data Anal. 2011;17(1):123-34. [PubMed ID: 20521166]. [PubMed Central ID: PMC2943572]. https://doi.org/10.1007/s10985-010-9171-z.
-
14.
Arano I, Sugimoto T, Hamasaki T, Ohno Y. Practical application of cure mixture model for long-term censored survivor data from a withdrawal clinical trial of patients with major depressive disorder. BMC Med Res Methodol. 2010;10:33. [PubMed ID: 20412598]. [PubMed Central ID: PMC2880122]. https://doi.org/10.1186/1471-2288-10-33.
-
15.
Peto R, Lee PN, Paige WS. Statistical analysis of the bioassay of continuous carcinogens. Br J Cancer. 1972;26(4):258-61. [PubMed ID: 5071187]. [PubMed Central ID: PMC2008655].
-
16.
Carrasco JMF, Ortega EMM, Cordeiro GM. A generalized modified Weibull distribution for lifetime modeling. Comput Statistics Data Analysis. 2008;53(2):450-62. https://doi.org/10.1016/j.csda.2008.08.023.
-
17.
Wang D. Maller RA, Zhou X, Survival analysis with long-term survivors. Statistic Methods Med Res. 2000;9:520.
-
18.
Abu Bakar MR, Salah KA, Ibrahim NA. Cure fraction, modelling and estimating in a population-based cancer survival analysis. Malaysian J Math Sci. 2008;2:113-34.
-
19.
Asano J, Hirakawa A, Hamada C. Assessing the prediction accuracy of cure in the Cox proportional hazards cure model: an application to breast cancer data. Pharm Stat. 2014;13(6):357-63. [PubMed ID: 25044997]. https://doi.org/10.1002/pst.1630.
-
20.
Ortega EMM, Barriga GDC, Hashimoto EM, Cancho VG, Cordeiro GM. A new class of survival regression models with cure fraction. J Data Sci. 2014;12(1):107-36.
-
21.
Bradburn MJ, Clark TG, Love SB, Altman DG. Survival analysis part II: multivariate data analysis--an introduction to concepts and methods. Br J Cancer. 2003;89(3):431-6. [PubMed ID: 12888808]. [PubMed Central ID: PMC2394368]. https://doi.org/10.1038/sj.bjc.6601119.
-
22.
Cox PR. Life Tables. Wiley Online Library; 1972.
-
23.
Kuk AYC, Chen CH. A mixture model combining logistic regression with proportional hazards regression. Biometrika. 1992;79(3):531-41.
-
24.
Sy JP, Taylor JM. Estimation in a Cox proportional hazards cure model. Biometrics. 2000;56(1):227-36. [PubMed ID: 10783800].
-
25.
Lu W. Maximum likelihood estimation in the proportional hazards cure model. Ann Inst Statistic Math. 2007;60(3):545-74. https://doi.org/10.1007/s10463-007-0120-x.
-
26.
Rama R, Swaminathan R, Venkatesan P. Cure models for estimating hospital-based breast cancer survival. Asian Pac J Cancer Prev. 2010;11(2):387-91. [PubMed ID: 20843121].
-
27.
Achcar JA, Coelho-Barros EA, Mazucheli J. Cure fraction models using mixture and non-mixture models. Tatra Mountains Math Publicat. 2012;51(1):1-9. https://doi.org/10.2478/v10127-012-0001-4.
-
28.
Othus M, Barlogie B, Leblanc ML, Crowley JJ. Cure models as a useful statistical tool for analyzing survival. Clin Cancer Res. 2012;18(14):3731-6. [PubMed ID: 22675175]. [PubMed Central ID: PMC3744099]. https://doi.org/10.1158/1078-0432.CCR-11-2859.
-
29.
Akhlaghi AA, Najafi I, Mahmoodi M, Shojaee A, Yousefifard M, Hosseini M. Survival analysis of Iranian patients undergoing continuous ambulatory peritoneal dialysis using cure model. J Res Health Sci. 2013;13(1):32-6. [PubMed ID: 23772014].
-
30.
Yu XQ, De Angelis R, Andersson TM, Lambert PC, O'Connell DL, Dickman PW. Estimating the proportion cured of cancer: some practical advice for users. Cancer Epidemiol. 2013;37(6):836-42. [PubMed ID: 24042025]. https://doi.org/10.1016/j.canep.2013.08.014.
-
31.
Rahimzadeh M, Baghestani AR, Gohari MR, Pourhoseingholi MA. Estimation of the cure rate in Iranian breast cancer patients. Asian Pac J Cancer Prev. 2014;15(12):4839-42. [PubMed ID: 24998549].
-
32.
Ture M, Tokatli F, Kurt Omurlu I. The comparisons of prognostic indexes using data mining techniques and Cox regression analysis in the breast cancer data. Expert Systems Applicat. 2009;36(4):8247-54. https://doi.org/10.1016/j.eswa.2008.10.014.
-
33.
Abadi A, Yavari P, Dehghani-Arani M, Alavi-Majd H, Ghasemi E, Amanpour F, et al. Cox models survival analysis based on breast cancer treatments. Iran J Cancer Prev. 2014;7(3):124-9. [PubMed ID: 25250162]. [PubMed Central ID: PMC4171826].
-
34.
Rezaianzadeh A, Peacock J, Reidpath D, Talei A, Hosseini SV, Mehrabani D. Survival analysis of 1148 women diagnosed with breast cancer in Southern Iran. BMC Cancer. 2009;9:168. [PubMed ID: 19497131]. [PubMed Central ID: PMC2699348]. https://doi.org/10.1186/1471-2407-9-168.
-
35.
Kuru B, Camlibel M, Gulcelik MA, Alagol H. Prognostic factors affecting survival and disease-free survival in lymph node-negative breast carcinomas. J Surg Oncol. 2003;83(3):167-72. [PubMed ID: 12827686]. https://doi.org/10.1002/jso.10264.
-
36.
Arpino G, Bardou VJ, Clark GM, Elledge RM. Infiltrating lobular carcinoma of the breast: tumor characteristics and clinical outcome. Breast Cancer Res. 2004;6(3):R149-56. [PubMed ID: 15084238]. [PubMed Central ID: PMC400666]. https://doi.org/10.1186/bcr767.
-
37.
Ziaei JE, Sanaat Z, Asvadi I, Dastgiri S, Pourzand A, Vaez J. Survival analysis of breast cancer patients in northwest Iran. Asian Pac J Cancer Prev. 2013;14(1):39-42. [PubMed ID: 23534759].
-
38.
Vahdaninia M, Montazeri A. Breast cancer in Iran: a survival analysis. Asian Pac J Cancer Prev. 2004;5(2):223-5. [PubMed ID: 15244529].
-
39.
Akbari A, Razzaghi Z, Homaee F, Khayamzadeh M, Movahedi M, Akbari ME. Parity and breastfeeding are preventive measures against breast cancer in Iranian women. Breast Cancer. 2011;18(1):51-5. [PubMed ID: 20217489]. https://doi.org/10.1007/s12282-010-0203-z.
-
40.
Akbari ME, Khayamzadeh M, Khoshnevis SJ, Nafisi N, Akbari A. Five and ten years survival in breast cancer patients mastectomies vs. breast conserving surgeries personal experience. Iran J Cancer Prevent. 2008;1(2):53-6.
-
41.
Faradmal J, Talebi A, Rezaianzadeh A, Mahjub H. Survival analysis of breast cancer patients using Cox and frailty models. J Res Health Sci. 2012;12(2):127-30. [PubMed ID: 23241526].
-
42.
Nafissi N, Saghafinia M, Motamedi MH, Akbari ME. A survey of breast cancer knowledge and attitude in Iranian women. J Cancer Res Ther. 2012;8(1):46-9. [PubMed ID: 22531513]. https://doi.org/10.4103/0973-1482.95173.
-
43.
Movahedi M, Haghighat S, Khayamzadeh M, Moradi A, Ghanbari-Motlagh A, Mirzaei H, et al. Survival rate of breast cancer based on geographical variation in iran, a national study. Iran Red Crescent Med J. 2012;14(12):798-804. [PubMed ID: 23483369]. [PubMed Central ID: PMC3587870]. https://doi.org/10.5812/ircmj.3631.
-
44.
Jafari-Koshki T, Mansourian M, Mokarian F. Exploring factors related to metastasis free survival in breast cancer patients using Bayesian cure models. Asian Pac J Cancer Prev. 2014;15(22):9673-8. [PubMed ID: 25520087].
-
45.
Momenyan S, Sadeghifar M, Sarvi F, Khodadost M, Mosavi-Jarrahi A, Ghaffari ME, et al. Relationship between Urbanization and Cancer Incidence in Iran Using Quantile Regression. Asian Pac J Cancer Prev. 2016;17(S3):113-7. [PubMed ID: 27165247].
-
46.
Peng Y, Dear KB, Denham JW. A generalized F mixture model for cure rate estimation. Stat Med. 1998;17(8):813-30. [PubMed ID: 9595613].
-
47.
Yamaguchi K. Accelerated Failure-Time Regression Models with a Regression Model of Surviving Fraction: An Application to the Analysis of "Permanent Employment" in Japan. J Am Statistic Assoc. 1992;87(418):284. https://doi.org/10.2307/2290258.
reply