1. Background
Cancer is a major concern in the world with an average of four deaths. Cervical cancer is the fourth most common cancer among women, and the seventh overall, with an estimated 528 000 new cases in 2012. As with liver cancer, a large majority (around 85%) of the global burden occurs in the less developed regions, where it accounts for almost 12% of all female cancers. High-risk regions, with estimated ASRs over 30 per 100 000, include Eastern Africa (42.7), Melanesia (33.3), and Southern (31.5), and Middle (30.6) Africa. Rates are the lowest in Australia/New Zealand (5.5) and Western Asia (4.4). Cervical cancer remains the most common cancer among women in Eastern and Middle Africa. There were an estimated 266 000 deaths from cervical cancer worldwide in 2012, accounting for 7.5% of all female cancer deaths. Almost 9 out of 10 (87%) cervical cancer deaths occur in the less developed regions. Mortality varies 18-fold among the different regions of the world with the rates ranging from less than 2 per 100 000 in Western Asia, Western Europe, and Australia/New Zealand to more than 20 per 100 000 in Melanesia (20.6), Middle (22.2), and Eastern (27.6) Africa (1, 2).
The results of research till 2010 show cervical cancer as one of the causes of death among women over 15 years old. Besides, the statistical results of this study show a drastic increase in the prevalence of this cancer (3). Researchers at the University of Manchester have reported a 40% increase in the prevalence of cervical cancer in young women in recent decades (4). Researchers in Eastern Europe have also found alarming signs of an increase in the disease in the Baltics, Romania, and Bulgaria (5). Cervical cancer is the most prevalent one in India (6). The frequency of this cancer in Iran is relatively less than that of other countries. According to the National Cancer Registry report of 2009, the prevalence of cervical cancer in Iran was 2.17 per 100 000 people and ranked 11th among cancers in Iranian females with a slight increase compared to the 2008 report (7). According to the statistics reported in 2017, the crude incidence rate of cervical cancer among women was 2.5, 1.7, and 15.1 cases per 100 000 in Iran, South Asia, and the world, respectively. Also, the crude death rate for cervical cancer was 1, 9.4, and 7.6 women per 100 000 in Iran, South Asia, and the world, respectively (8).
Survival analysis, as one of the most important statistical methods in analyzing data collected over time, attracted the attention of many statisticians (9-11). In the usual methods of survival analysis, it is assumed that all individuals in the population under study are susceptible to the aimed event, while there are times when some people in the community are immune to the incident and do not experience it until the end of their life. These individuals are referred to as "safe or improved" groups. Therefore, in this case, the basic assumption of the usual methods of survival analysis is abandoned. To study such a population, which consists of 2 susceptible and safe subgroups, survival analysis methods known as healing models should be used.
In such studies, particularly in cancer research, cure models are used to analyze the data regarding the time till the occurrence of an event, from which a portion of the population is safe. Members of the long-term survival group are those, who are immune to the event. It is worth noting that, in the case of the non-existence of safe people, the models presented in the mixture cure model can turn back to the standard survival models (12-14). These models can be either parametric or nonparametric. The main goal in the cured mixture models is to estimate the proportion of cured or safe individuals (who do not experience the desired event at all), the survival function for those exposed to the event (the susceptible individuals), and the factors affecting these two cases (12, 13). In such a model, the probability of being cured can only be gained through maximum likelihood estimation; in other words, the safety of individuals cannot be determined (13, 14).
Due to the random pattern of censored data, it is not easy to differentiate the safe people from the censored data because censored observations result from excluding people from the study, missing or losing information, or insufficient time to follow up a study due to ethical or financial limitations. In case the cured individuals exist in the population under study, they have a relatively long survival time; in other words, these individuals will not be affected by the aimed event till the end of the study. So, these people are those who have a long censorship time (13).
One of the presuppositions in Cox's proportional risk model is that all individuals in the study will experience the aimed event until the end of the study (15). However, sometimes a significant proportion of individuals do not experience the event during the follow-up period. In incurable chronic diseases that maintain their progression, all the patients will gradually die. Though, sometimes things are different. For example, all those who are infected by HIV, are not affected by it; this means that a percentage of the individuals are safe. In such cases, the Cox risk model will not be appropriate because one of its main presumptions is rejected. Therefore, the cure models must be used here as they do not need a certain presumption (13).
In the survival analysis, when mortality reaches the maximum and, then, gradually decreases after a finite period, it is better to use models, which have a non-uniform failure rate, e.g. log-logistic and log-normal models (16, 17). In the present study, the risk function has such a pattern; that is, it increases at first and, then, decreases after a while. Thus, using Cox-Weibull and exponential models will not be the right choice as the log-logistic and log-normal models can better estimate the data.
2. Objectives
Since a lot of patients with cervical cancer have long-term survival, this study tried to examine and compare the cure models through 3 parametric models, i.e. Weibull, log-normal, and log-logistic models to determine the effect of individual characteristics on the cure rate of patients with cervical cancer.
3. Methods
The research sample of the present study included 109 female patients with cervical cancer referred to Motahhari hospital of Urmia from 2004 to 2014. The required data were obtained through checklists filled out by the patients. It is also worth noting that Motahhari hospital is the only treatment center for patients with cervical cancer in West Azerbaijan Province, Iran. Those patients who were not native to the province were excluded from the study. The survival time was considered from diagnosis to the patient’s death. Therefore, those who survived until the end of the study or were excluded from the study due to other reasons or died of a reason other than cancer were considered censored observations. The personal characteristics were age, relapse, radiotherapy, age of marriage (over 20 and under 20), stage of cancer, and type of cancer. Besides, the information regarding the patients’ survival was obtained through telephone calls. In this study, the AIC criterion was used to compare the efficacy of log-normal, log-logistic, and Weibull parametric models. The AIC criterion, proposed by Akaike in 1974, was used to measure the goodness of fit (13, 18). The AIC criterion measures the degree of interaction between the complexity of a model and the fitting of a model. The AIC value for the models used in this research was calculated, using the following formula:
where n is the number of parameters in the model depending on the type of model used. The lower the AIC, the better will be the performance of the model. The following formulas were used to calculate the survival of the parametric models (16).
The Weibull distribution function:
where γ and λ are the shape and scale parameters of this distribution, respectively.
The log-logistic distribution function:
where p and λ are the shape and scale parameters of this distribution, respectively.
Log-normal distribution function:
Similarly, cure models can be divided into two types: mixture and non-mixture cure models. In the mixture models, the population is assumed to be composed of k subgroups, and the distribution of survival time of members in each subgroup is considered to be different from that of the others. So, let
The non-mixture models, on the other hand, were proposed for those communities, in which the cumulative distribution function of the survival of the entire population is improper; in other words, the total volume does not equal 1 in the cumulative distribution function. Therefore, the total volume difference (in the cumulative distribution function of survival time of individuals) being 1 shows the proportion of cured people in these societies (19). In the mixture cure models, the population is made up of two at-risk (susceptible) and immune (safe) heterogeneous subpopulations. In such models, it is assumed that each person is at risk of the aimed event with a probability of p and is not at risk of the event with a probability of 1-p (safe or cured). The survival function for community members in the mixture cure models is as follows:
where 1-p is the cure rate, t is a random variable representing the occurrence time of the event, and S (t) is the survival function of the exposed individuals. Then,
4. Results
The present study is a historical prospective study, including 109 female patients with cervical cancer, who were referred to the Motahari University Hospital of Urmia from 2002 to 2014. The mean and standard deviation of diagnostic time of the patients was 50.1 ± 11.7 years. The mean, standard deviation, and median of follow-up time were 38.23 ± 32.20 and 27.1 months (2 months = min and 132 months = max). The mean, standard deviation, and median age of marriage were 18.9 ± 4.4 and 18 years old, from which 70 (64.2%) were married at the age of fewer than 20 years, 99 cases (90.8%) were SCC, and 10 cases (9.2%) were adenocarcinoma in terms of cancer histology.
According to the reports, 33 patients (30.3%) suffered and 76 cases (69.7%) did not suffer from relapse. Besides, 92 cases (84.4%) were under radiotherapy and 17 (15.6%) did not receive radiotherapy. According to FIGO grading, 43 (39.4%) cases were graded I, 47 patients (43.1%) were graded II, and 19 (17.4%) ones were graded III and higher. Thirty cases (27.5%) died during the study; besides, 79 cases (73.5%) were considered to be right-censored observations. A summary of the results is presented in Table 1.
| Variable | No. (%) |
|---|---|
| Age at diagnosis | |
| < 50 | 49 (45.0) |
| ≥ 50 | 60 (55.0) |
| Recurrence of the disease | |
| No | 76 (69.7) |
| Yes | 33 (30.3) |
| Radiotherapy | |
| No | 92 (84.4) |
| Yes | 17 (15.6) |
| Age of marriage | |
| < 20 | 70 (64.2) |
| ≥ 20 | 39 (35.8) |
| Histology type | |
| Adenocarcinoma | 10 (9.2) |
| SCC | 99 (90.8) |
| FIGO stage | |
| I | 43 (39.4) |
| II | 47 (43.1) |
| III | 19 (17.4) |
Characteristics of the Patients with Cervical Cancer
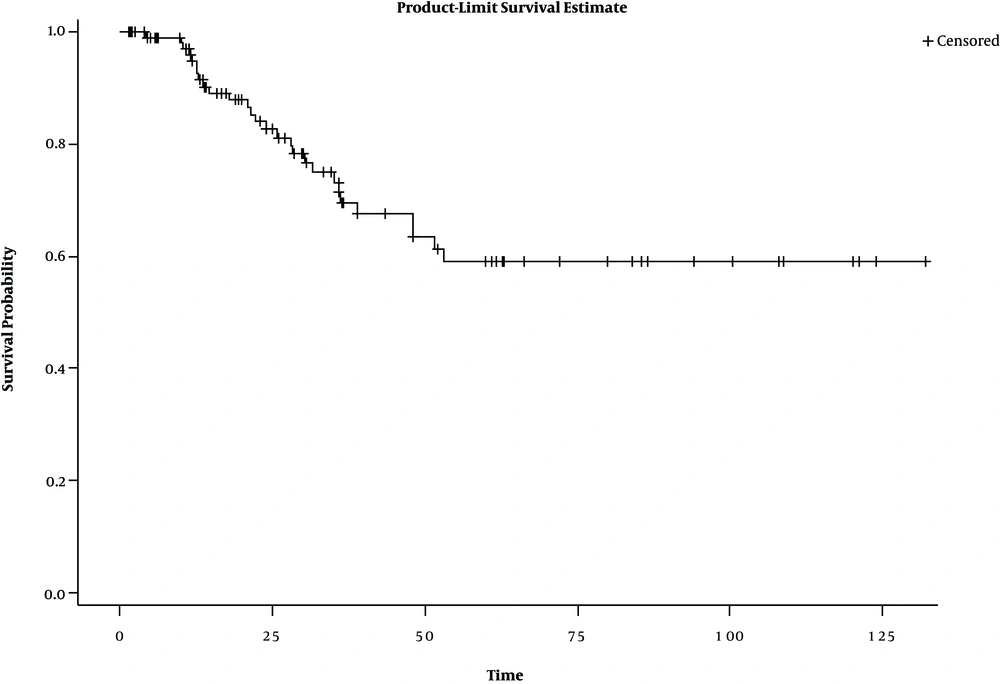
Kaplan-Meier diagram is one of the most common methods of examining immune (cured) individuals. The diagram becomes a horizontal line before reaching zero in case of the presence of immune patients (13). Figure 1 shows the presence of safe people in the research data.
One of the most important reasons for using the cure model is to examine the cured fraction. The results of the observations showed that the safe subjects formed 40% of the research sample, a statistically significant rate (P = 0.05) (Table 2).
| Safe Patients’ Ratio | Fiducial Interval | P-Value | ||
|---|---|---|---|---|
| Upper Limit | Lower Limit | |||
| Cox cure model | 0.40 | 3.25 | 0.29 | 0.05 |
Results of Examining the Existence of Immune Subjects in the Cure Model
To fit the model with these data, the univariate mixture cure model with Weibull, log-logistic, and log-normal functions was used. Also, the Logit’s function was used to estimate the cure ratio. A summary of the results is represented in Table 3.
| Risk factors | Weibull Model | Log-Logistic Model | Log-Normal Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cure Chance | Fiducial Interval | P-Value | Cure Chance | Fiducial Interval | P-Value | Cure Chance | Fiducial Interval | P-Value | ||||
| Upper Limit | Lower Limit | Upper Limit | LowerLimit | UpperLimit | LowerLimit | |||||||
| Age at diagnosis | ||||||||||||
| < 50 | Base group | Base group | Base group | |||||||||
| ≥ 50 | 3.91 | 12.07 | 1.27 | 0.017 | 3.71 | 12.71 | 1.08 | 0.036 | 3.60 | 12.26 | 1.05 | 0.040 |
| Recurrence of the disease | ||||||||||||
| No | Base group | Base group | Base group | |||||||||
| Yes | 10.34 | 39.15 | 2.73 | 0.000 | 9.32 | 39.88 | 2.18 | 0.002 | 8.86 | 36.72 | 2.13 | 0.002 |
| Radiotherapy | ||||||||||||
| No | Base group | Base group | Base group | |||||||||
| Yes | 0.34 | 1.48 | 0.080 | 0.151 | 0.24 | 1.76 | 0.03 | 0.162 | 0.24 | 1.88 | 0.03 | 0.174 |
| Age of marriage | ||||||||||||
| < 20 | Base group | Base group | Base group | |||||||||
| ≥ 20 | 0.15 | 0.68 | 0.03 | 0.014 | 0.17 | 0.80 | 0.03 | 0.026 | 0.190 | 0.95 | 0.03 | 0.044 |
| Histology type | ||||||||||||
| Adenocarcinoma | Base group | Base group | Base group | |||||||||
| Scc | 3.77 | 45.02 | 0.31 | 0.290 | 3.08 | 0.20 | 0.412 | 2.54 | 54.26 | 0.11 | 0.545 | |
| FIGO stage | ||||||||||||
| I | Base group | Base group | Base group | |||||||||
| II | 0.54 | 1.78 | 0.16 | 0.311 | 0.48 | 1.72 | 0.13 | 0.263 | 0.46 | 1.62 | 0.13 | 0.236 |
| III | 5.83 | 37.26 | 0.91 | 0.062 | 7.66 | 112.5 | 0.52 | 0.135 | 6.27 | 66.18 | 0.59 | 0.125 |
the Univariate Analysis of the Cure Parametric Models
Patient's age, age of marriage, and relapse of the disease factors in the univariate model became significant on the long-term survival function of patients with cervical cancer; this means that the patients older than 50 years, who experienced relapse and married at ages over 20 years, were more prone to risk than patients younger than 50 years not experiencing a relapse, and married at ages under 20 years. For example, these results in the log-logistic model indicate that the risk of mortality or failure for patients over 50 years in the long-term survival was 71.3 times higher than that of patients less than 50 years old. Moreover, the risk of mortality in patients married at ages over 20 years was 0.15 times higher than that of patients married under 20 years. Besides, the risk of failure for those who have experienced relapse was 32.9 times higher than those who have not. The results with the Weibull and log-normal models were also similar to the results of the log-logistic model (Table 3). The precursor method PR = 0.15 was used to choose the best multivariate survival cure model, the results of which are presented in Tables 4 and 5.
| Risk factors | Weibull Model | Log-Logistic Model | Log-Normal Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cure Chance | Fiducial Interval | P-Value | Cure Chance | Fiducial Interval | P-Value | Cure Chance | Fiducial Interval | P-Value | ||||
| Upper Limit | Lower Limit | Upper Limit | Lower Limit | Upper Limit | Lower Limit | |||||||
| Recurrence of the disease | ||||||||||||
| No | Base group | Base group | Base group | |||||||||
| Yes | 7.93 | 27.70 | 2.27 | 0.001 | 7.35 | 28.11 | 1.92 | 0.003 | 7.23 | 27.86 | 1.87 | 0.009 |
| Age of marriage | ||||||||||||
| < 20 | Base group | Base group | Base group | |||||||||
| ≥ 20 | 0.12 | 0.66 | 0.02 | 0.013 | 0.13 | 0.75 | 0.02 | 0.023 | 0.15 | 0.94 | 0.02 | 0.043 |
Multiple Analysis of the Cure Parametric Models for Susceptible Subjects
| Risk Factors | Weibull Model | Log-Logistic Model | Log-Normal Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Relative Risk | Fiducial Interval | P-Value | Relative Risk | Fiducial Interval | P-Value | Relative Risk | Fiducial Interval | P-Value | ||||
| Upper Limit | Lower Limit | Upper Limit | Lower Limit | Upper Limit | Lower Limit | |||||||
| Recurrence of the disease | ||||||||||||
| No | Base group | Base group | Base group | |||||||||
| Yes | 3.40 | 8.97 | 1.28 | 0.013 | 8.96 | 43.28 | 1.85 | 0.006 | 3.62 | 9.23 | 1.42 | 0.007 |
| Age of marriage | ||||||||||||
| < 20 | Base group | Base group | Base group | |||||||||
| ≥ 20 | 2.84 | 18.81 | 0.43 | 0.274 | 2.54 | 23.93 | 0.27 | 0.410 | 1.44 | 6.70 | 0.31 | 0.633 |
Multiple Analysis of the Cure Parametric Models for Susceptible Subjects
Variables that were significant in the univariate analysis were analyzed with the multivariate test. A summary of the final results of the Weibull, log-normal, and log-logistic survival models is presented in Tables 4 and 5. In these models, age of marriage and relapse were recognized as two prognostic factors in long-term survival (safe subjects). The relapse factor was the only prognostic factor for short-term survival (susceptible subjects) of patients with cervical cancer. According to the log-logistic model, as the best fit model, the risk of failure in long-term survival in patients married at ages more than 20 years was shown to be 0.12 times higher than that of those married under age 20 years. Also, the risk of failure was 6.7 times higher for patients who have experienced relapse compared to those who have not; in other words, considering the long-term survival, the risk of failure is higher for those patients who have experienced a relapse. However, in the short-term survival (susceptible subjects), the relapse was the mere significant factor. This means that the risk of mortality was 8.96 times higher for those patients who have experienced a relapse. In both parts of the model, the relapse factor was significant at a 0.05 significance level. Therefore, relapse factor can both increase the likelihood of failure for safe subjects and reduce the survival of susceptible patients. Moreover, the age factor in those immune subjects who were married at ages over 20 years made them more prone to failure but did not significantly affect the survival of the susceptible patients (P = 0.410).
Table 6 shows the results of comparing the AIC criterion of the fit models to determine the best cure model. According to the results, the log-logistic parametric cure model is the most suitable for analyzing the data regarding cervical cancer survival in West-Azerbaijan Province.
| Model | AIC Model |
|---|---|
| Weibull parametric model | 300.2 |
| Log-normal parametric model | 299.9 |
| Log-logistic parametric model | 128 |
Comparing the Akaike Information Criterion for the Fitted Cure Models
5. Discussion
Cervical cancer is the fourth most common cancer among women in the world (22). The most important reported factors in the survival of cervical cancer patients are diagnosis at older ages, frequent human papillomavirus infections, and tumor histology (23-25). In the present study, the mean (SD) of diagnosis time of 109 patients was 1.50 % (17.7). Besides, the mean and standard deviation of the follow-up time was 38.23 ± 32.5 months.
Many studies have been conducted on cervical cancer. Although medical researchers often tend to use the Cox Proportional Hazard model in their analysis of the effect of explanatory variables on patient survival instead of similar parametric models (26, 27); a systematic study on cancer journals showed that only 5% of studies using the Cox model have examined the required key assumptions for this model (28). The Cox proportional hazards model requires all its assumptions to exist; otherwise, the results cannot be reliable. Therefore, the log-normal, Weibull, and log-logistics parametric models can be a better choice in such situations because they assume a specific distribution for the time variable, and do not need to assume the proportional hazards to fit the model (10, 29).
One of the key assumptions in the Cox proportional hazard model is that all subjects in the study will eventually experience the aimed event (15). This assumption can be violated in cases that are safe patients in the research sample. In such cases, it is more recommended to use the cure models, which do not require this specific assumption (13). The cured subjects in the research sample have a relatively longer survival time; in other words, they will not be affected by the aimed event till the end of the study; so, these people are those with long-lasted censorship (13).
This study aimed at evaluating the use of heuristic parametric models to determine the effect of individual characteristics on the cure rate of patients with cervical cancer. Also, the models were compared based on Akaike’s criteria. Based on the results, the age of marriage and relapse were identified as two important factors in the long-term survival of patients with cervical cancer; in other words, subjects married at ages over 20 years were more likely to fail than those who were married at ages under age 20. Moreover, the results regarding the long-term survival group indicated that the patients experiencing relapse were more likely to fail than those without relapse. The analysis of the short-term survival portion also showed the relapse rate to be significant, meaning that the risk of mortality for the subjects who have experienced relapse was higher than those who have not. In other words, patients with an experience of relapse died faster than patients with no relapse experience.
Federico et al. in their study in the Netherlands examined the relationship between age, race, medical budget, and cervical cancer in 125 patients with cervical cancer in 2010. Their results showed no relationship between race, medical knowledge, cancer screening pattern, and the rate of survival. However, the survival chance of cases diagnosed at age over 65 was lower (24).
This report included 99 (90.8%) patients with SCC and 10 (9.2%) adenocarcinoma cases. In a study by S.Bulk et al., the survival rate of females with cervical cancer indicated that the occurrence of SCC decreases when the occurrence of adenocarcinoma is irreversible. Patients with adenocarcinoma survive less than SCC cases (30). These findings are incompatible with our results as we observed no significant relationship between the type of cancer and the long-term survival of the patients.
The findings of the present study indicated that more studies need to be conducted in this regard. However, there is no way to determine which model is the most suitable. For the present study, however, the log-logistic was the best fitting model; so, it can be used as a substitute for the Weibull and log-normal models.
The results of the present study showed that marriage at ages 20 and over can be an important factor in increasing the risk of mortality and failure. It is recommended that the control and prevention of this disorder be considered seriously; besides, treatment must begin before the occurrence of any relapse. Given that the assumption of proportionality of hazards in the data was rejected and based on the comparisons, it can be concluded that the log-logistic model combined with the Logit’s function can be used as a substitute for Cox and Weibull and log-normal models to analyze the survival of patients with cervical cancer.
5.1. Conclusions
Contrary to the Cox model, the cure models can be used to analyze the cervical cancer data in suitable conditions and also to isolate the short-term survival from long-term survival and identify the factors affecting each. This statistical test can help decision-makers by providing them with more accurate results.