1. Background
Product life cycle (PLC) is a concept widely used in the literature. In theory, at least two contradictory definitions have been put forward for a product's life cycle. The first definition refers to production from the raw material, use, and finally, to the disposal of a product, called the physical PLC (1). The second definition is based on the PLC theory, which represents the sales volume of a product over time (2). Some studies have considered four stages for PLC: introduction, growth, maturity, and decline (1); however, some others studies have introduced the five stages for PLC: development, introduction, growth, maturity, and decline. These stages are observed for all services and products, from automobiles to health-centric products such as medicines.
Each PLC stage encompasses more specific sub-stages, depending on the type of product or service (3). When a product is introduced to the market for the first time, a low sales volume is expected because of individuals’ lack of awareness; however, with more promotion and advertisement, the sales may grow, and the growth stage starts. When competition increases and market saturation is reached, the sales growth decreases, and the maturity stage emerges. In this stage, the total market size increases due to increasing information about products. Then the decline stage comes, and product sales drop rapidly. The practical management of these stages is required to increase sales over time and postpone the decline stage (4).
Many studies classified the sales patterns of different products, including pharmaceutical products. Although the PLC patterns vary in different products and cannot be generalized, the PLC concept is still one of the practical frameworks in marketing (5). The PLC patterns and the investigation of the curve shape can be considered efficient tools to analyze the market trends in any industry, including pharmaceuticals, and could evaluate the system performance (6). Many factors may affect the shape of the PLC curves, the recognition of which is of paramount importance for efficient product management and boosting firm market advantages (7).
1.1. Iranian Pharmaceutical Industry
Compared to developing countries, the Iranian pharmaceutical market has grown significantly, and the market is expanding rapidly (8, 9). Iran had about 40 pharmaceutical plants in 1979, most of which were the subsidiaries of international companies producing 30% of Iran’s pharmaceutical market under license. Following the revolution of Iran in 1979, most international companies left the country, and medicine production continued as generic production by domestic firms, which could improve access to medicines, including cost-effective medicines. In 2019, this domestic industry produced 95% of the medicines in Iran (10-12). Meanwhile, systemic antibacterial use has expanded more in Iran than in other countries. Increasing antibiotic resistance and growth in spending on medicines is the most unreasonable consequence of antibiotic use in society. The lack of up-to-date data about medicine usage has aroused some evidence-based policies across the country (13). We studied the sales of systemic antibiotics (antibiotics taken orally or given by injection) by different classes over 16 years (2002 - 2017) in Iran. Using a generalized linear model, we detected factors affecting PLC over time and then analyzed the within- and between- effects of each identified factor.
1.2. Conceptual Framework
The early research on the PLC of pharmaceutical products goes back to 1976, when Cox first tried to identify the pattern of 754 "ethical" medicine sales. He found six different behaviors in the sales graph of pharmaceutical products, among which the polynomial curves were the main sales patterns (14). After that, Jernigan et al. showed that the bell-shaped curve is the most common form of medicine sales patterns (15). Grabowski and Vernon studied the sales patterns of 100 new medicines entered the U.S. market in 1990. They revealed that the increasing price of drugs and covering the research and development costs were higher compared to the past, thereby increasing competition and shortening the product life cycle of medicines (16). In 1994, Bergstrom and Hoog investigated the effect of switching from prescription medicines to over-the-counter (OTC) ones on the PLC curves. Their findings indicated that 11 out of 15 switches influenced the PLC curves and increased sales (17). In a cross-sectional study of the six pharmaceutical companies during 1983-1993, Bauer and Fisher (5) spared efforts to obtain a general typology for medicines. In their study, the classic PLC curve with a short growth phase related to late movers (after the brand medicine) was the most common pattern in ACE Inhibitor medicines. Moreover, the pioneer producer gained more profit during PLC than generic producers (5). Fischer et al. documented that the brand products reached peak sales later and that the height of the peaks for brand products was higher than generic medicines, leading to higher cumulative sales (18). However, Hemphill and Sampat suggested that brand drugs, especially blockbusters, have a shorter market life than generic ones due to patent challenges and that their sales decrease over time (19). Abdollahiasl et al. and Mousavi et al. reported that competitors' numbers and prices could affect pharmaceutical sales patterns (20, 21).
The above-mentioned studies have highlighted ‘competition’ as an essential factor to affect product sales over time.
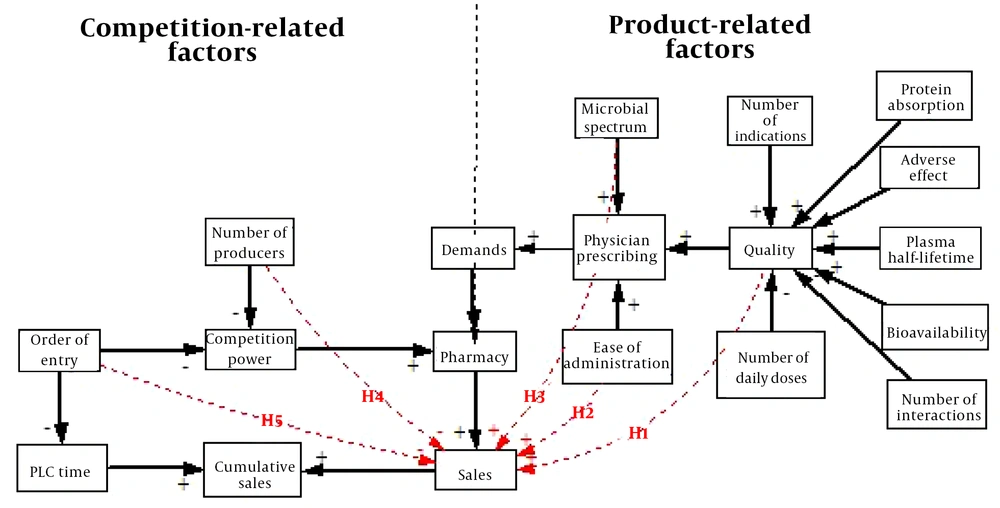
In the present study, ‘the number of competitors’ and ‘the order of entry into the market’ were competition-related factors with likely effects on the PLC of generic antibiotics. Previous studies (5, 20, 22) have addressed some product-related factors affecting PLC. For example, Fisher examined quality as an essential factor in decreasing time to arrive to peak sales and increase peak sales. In the present study, we dealt with each of the seven following indicators to measure quality: bioavailability, protein absorption, plasma half-life time, number of indications, frequency of side effects, number of interactions, and medicine dosage (18). Concerning antibiotics, the microbial spectrum is another crucial product characteristic determining the prescription of this category and affecting PLC. The microbial spectrum determines the range of drug effectiveness and inhibitory effects against bacteria (23). The most global usage of antibiotics during 2000 - 2010 was reported for broad-spectrum antibiotics (last-resort) such as Carbapenem (22). Physicians frequently use wide-spectrum antibiotics to prevent infectious cases to support gram-positive and gram-negative bacteria (24). This study hypothesized that the microbial spectrum as a specific characteristic of antibiotics positively affects cumulative sales. Masoud et al. found that injection prescription was lower than oral use of such drugs due to their painful administration and more side-effects (25). Accordingly, we considered the dosage form (oral or injectable) as another factor affecting PLC in this study.
According to the above-mentioned studies, we considered two-factor categories affecting the PLC curves, according to which five hypotheses were formed:
(1) Product-related factors, including quality, microbial spectrum, and dosage forms (ease of administration). For these factors, we tested the following three hypotheses:
H1: Medicines with higher quality have more peak sales and cumulative sales during PLC and reach peak sales later.
H2: Oral forms of medicines have more incremental peak sales than injectable ones and reach peak sales later during PLC.
H3: Antibiotics with a broader microbial spectrum have more incremental peak sales than narrower microbial spectrum and reach peak sales later.
(2) Competition-related factors, including number of competitors and arrangement of entry. In this regard, we also tested the two following hypotheses:
H4: More competitors lead to fewer incremental peak sales and reach peak sales sooner.
H5: Later entry into the market leads to fewer incremental peak sales and reach peak sales later compared to earlier entrants.
The following conceptual framework was used in the present study (Figure 1).
1.3. Generalized Linear Model (GLM)
Various computer models in machine learning and statistics can predict outcomes such as logistic regression, decision tree, artificial neural network (ANN), and Bayesian networks (26). One of the estimation approaches highly applicable in medical, social, and biological sciences is the generalized linear model (GLM) (27). GLMs can predict the relationship between dependent and non-dependent variables for more complicated data, such as nonlinear and non-normal variables. The latter advantage is significant because, in many cases, the Gaussian normality of the data is inappropriate, and researchers cannot analyze them by using traditional methods such as linear regression (28). GLM is a suitable approach in social sciences since many of the variables in this field, such as binary and polynomial or non-normal variables (29), are categorical. For example, Terui et al. (30) developed a dynamic generalized linear model to forecast the future sales of brand products. Further, Latimore et al. (31) employed GLM to analyze the predictors of methamphetamine sales among young users in Thailand. Moreover, Ngufor et al. (32) studied the integration of GLM and machine learning approaches and developed a mixed-effect machine learning (MEml) model to predict the hemoglobin A1C in diabetic patients.
As a typical linear model, the linear regression model is the basis of GLMs (33). Unlike traditional linear methods such as linear regression, GLMs do not require data to be in natural scales or a constant variance structure. They are more flexible and adopt better approaches to analyzing complex data and nonlinear relationships belonging to different probability distributions such as negative binomial, gamma, or Poisson distribution (34). GLMs can show each coefficient’s value for categorical predictors coded in the model. In other words, each input usually has multiple associated coefficients, corresponding to each categorical value to be demonstrated in these models (28).
In the present study, besides detecting the PLC patterns, a generalized linear model was proposed to analyze differences estimating the effects on the sales curves. This study was a time-series cross-sectional analysis of antibiotics sales data in Iran. To this end, three main objectives were considered: (1) identifying and classifying the PLC patterns of generic antibiotics; (2) detecting factors affecting the PLC patterns; and (3) proposing a generalized linear model to estimate the effect of factors on the area under the PLC curve (cumulative sale), peak height (sales in peak time), and time to reach peak sales.
GLM is the generalization of traditional linear models and encompasses three main components:
(1) A linear component similar to traditional linear formula:
xi = A column vector of covariates for observation i
β = A column vector i of unknown coefficients
(2) Function g shows how "y" as a response is related to the linear predictor i:
(3) Each response variable (y1, y2 ...) has a probability distribution according to the following variance function:
Φ = dispersion parameter (constant). The probability distributions include the normal, Gaussian, inverse Gaussian, binomial, Poisson, and gamma distributions (35, 36).
2. Methods
2.1. Sample and Data Collection
The present study was conducted in three phases using time series data and market information. In the first phase, the numerical sales of 261 generic antibiotic medicines were assessed in Iran during 2002 - 2017. We acquired information about the sales of antibiotics from the Ministry of Health and Medical Education (MOHME).
In this phase, we collected all sales information about different classes of antibiotics based on the anatomical therapeutic chemical (ATC) classification domestically produced during the concerned period.
In the second phase, we extracted information about each domestic antibiotics manufacturer, and the medicines with sales information for less than ten years were excluded. Then we plotted the data using Origin Pro 2018 software (37) and the regression line fitted with an R-square > 0.8 for each graph (18). Accordingly, different PLC typologies for generic antibiotic medicines were identified.
In the last phase of this study, we examined the impact of the product-related and competition-related factors (Figure 1) on the PLC curves. We used Pearson’s coefficient and generalized linear model for all PLC curves and those with one-peak sales patterns.
2.2. Data Analyses
The dataset in this study included all systematic antibiotics in Iran, for which sales data for above ten years were available (n = 261). The impacts of various factors on the PLC of the following antibiotics were examined:
PLC type1 (classification sale patterns based on the complexity of curves: 1 = linear pattern, 2 = binomial pattern, 3 = one-peak pattern, 4 = two-peak pattern, and 5 = multi-peak pattern); PLC type 2 (classification of sales patterns by their slope: 1 = positive slope only in sales pattern, 2 = positive and negative slope in sales pattern, and 3 = only negative slope in sales pattern), cumulative sales (under the PLC curve over time), cumulative market share, the order of the entry (among other domestic manufacturers), number of producers (during all PLC period), and antimicrobial spectrum (The antibiotics were classified into four categories: 1 = narrow spectrum, 2 = moderately broad-spectrum, 3 = broad-spectrum, and 4 = very broad spectrum (38)); ease of administration (1 = oral antibiotics, 2 = parenteral antibiotics). The quality-index includes seven indicators (Q = X1 + X2 + X3 + X4 + X5 + X6 + X7): Bioavailability in percent (X1), Protein absorption in percent (X2), Plasma half-lifetime in hours (X3), Number of approved indications (X4), 1/Frequency of side-effects in percent (X5), 1/Number of dangerous interactions (X6), 1/number of intakes of medicine per day (X7).
Besides collecting these variables for all medicines, we collected the following data for the drugs with one peak in the PLC curves: Time to reach sales peak, sales volume in peak time, and market share in peak time.
2.3. GLM Analysis
This study used a generalized linear model by SPSS Modeler version 18.0 to achieve the factor impact on the PLC curves. We combined GLM with a machine learning technique to increase model performance by tracking the model fitness in training and testing datasets and providing acceptable training processes (28, 32). For this purpose, the SPSS Modeler separated the data into two categories: (1) training (70%) and (2) testing (30%) (39), which provided an infrastructure for the GLM analysis. In the next step, to analyze the variable impacts on the PLC curves, a GLM was developed. The validation procedure is essential in the machine learning approach to assess a model's accuracy performance, indicating how well the testing data learn from training data (40). We used the accuracy, error values, and correlation coefficients of the testing and training datasets to track acceptable machine learning processes and validate the models. The analysis was performed with SPSS modeler software version 18.0 (28).
3. Results
3.1. Descriptive Statistics
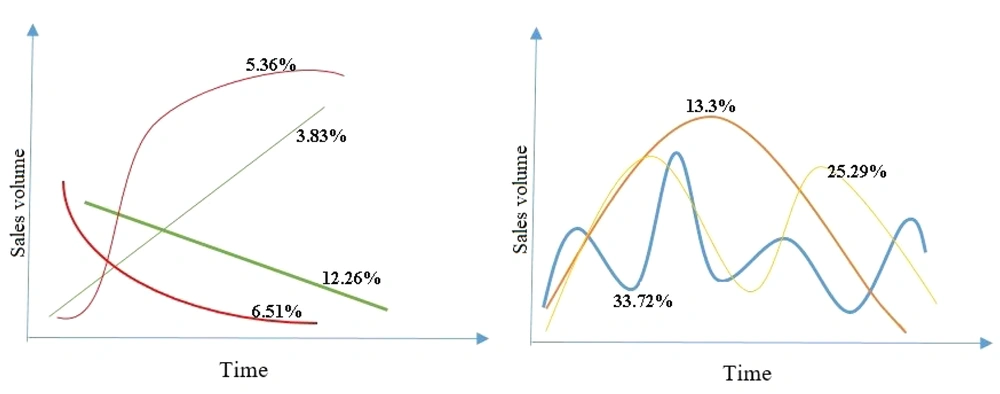
Some specifications of the 261 antibiotics are presented in Appendix 1. We investigated the sales pattern of each antibiotic produced by each domestic company. Among 280 medicines, including all dosage forms with sales information for above ten years, 19 medicines (6%) had sales patterns not fitted any regression line. The remaining 261 medicines fitted a regression line with an R-square > 0.8. In this regard, four general sale patterns were detected: 16% of the medicines had linear sales growth with a positive and negative slope; 11.87% had binomial sales growth patterns; 13.3% one peak sales pattern, 25.29% two peak sales patterns; and 33.72% had an oscillating sales pattern (Figure 2).
3.2. Correlation Results
The results of correlation between the research variables are presented in Table 1.
| Variables | All PLC | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 1. PLC type 1 | 1 | - | - | - | - | - | - | - | - | - | - | - |
| 2. PLC type 2 | -0.333 a | 1 | - | - | - | - | - | - | - | - | - | - |
| 3. AE | 0.142 b | -0.120 | 1 | - | - | - | - | - | - | - | - | - |
| 4. PLC time | -0.057 | 0.183 a | -0.628 a | - | - | - | - | - | - | - | - | - |
| 5. CS | 0.076 | -0.008 | -0.010 | 1 | - | - | - | - | - | - | - | - |
| 6. CMS | -0.136b | -0.142b | -0.081 | -0.024 | 1 | - | - | - | - | - | - | - |
| 7.NC | 0.095 | 0.019 | 0.524 a | 0.249 a | -0.096 | 1 | - | - | - | - | - | - |
| 8. EA | 0.166b | -0.100 | -0.218 a | -0.202 a | 0.094 | -0.375 a | 1 | - | - | - | - | - |
| 9.MS | 0.195 a | -0.250 a | 0.195 a | 0.007 | -0.076 | 0.108 | 0.116 | 1 | - | - | - | - |
| 10. Quality | 0.168b | -0.127 | 0.105 | 0.047 | -0.039 | -0.048 | -0.098 | 0.111 | 1 | - | - | - |
| One Peak PLC | ||||||||||||
| 11. SP | - | - | 0.286 | 0.937 a | -0.360 | 0.518 a | - | - | - | 1 | -0.064 | |
| 12. MSp | - | - | -0.567 a | -0.454b | 0.810 a | -0.862 a | - | - | - | -0.438b | 1 | -0.023 |
| 13. TP | - | - | 0.146 | -0.108 | 0.058 | 0.065 | - | - | - | - | - | 1 |
| 3. AE | - | - | 1 | - | - | - | - | - | - | - | - | - |
| 4. CS | - | - | 0.136 | 1 | - | - | - | - | - | - | - | - |
| 5. CMS | - | - | -0.511 a | -0.325 | 1 | - | - | - | - | - | - | - |
| 6. Producers | - | - | 0.687 a | 0.531 a | -0.706 a | 1 | - | - | - | - | - | - |
| 7. EA | - | - | -0.290 | -0.399b | 0.503 a | -0.564 a | 1 | - | - | -0.460b | 0.676 a | 0.267 |
| 8. MSp | - | - | 0.191 | -0.134 | 0.161 | 0.058 | 0.390b | 1 | - | -0.050 | 0.198 | 0.248 |
| 9. Quality | - | - | 0.230 | -0.034 | -0.133 | 0.294 | -0.071 | -0.210 | 1 | -0.081 | -0.259 | 0.184 |
Abbreviations: AE, arrangement of entry; CS, cumulative sales; MS, market share; CMS, cumulative market share; NC, number of competitors; EA, ease of administration; MSp, microbial spectrum; SP, sales amount in peak time; TP, time to reach peak sales.
a P < 0.01
b P < 0.05
3.3. GLM Analyses
According to Table 2, R-square is 0.778 (training dataset) and 0.803 (testing dataset) for all PLC curves and 0.989 (training dataset) and 0.999 (testing dataset) for one-peak PLC curves. The testing dataset’s higher R-square and smaller error values indicated excellent machine learning processes (28). Further information is presented in Table 2.
| Target | R2 | Min E | Max E | ME | MARE | SD |
|---|---|---|---|---|---|---|
| Log cumulative sales | ||||||
| GLM -training dataset of all curves | 0.778 | -1.549 | 1.558 | 0.0 | 0.436 | 0.556 |
| GLM -testing dataset of all curves | 0.803 | -1.239 | 1.131 | 0.0 | 0.445 | 0.555 |
| GLM-training set of the one peak curves | 0.989 | 0.999 | 0.322 | 0.005 | 0.078 | 0.123 |
| GLM -testing set of the one peak curves | 0.999 | -0.167 | 0.111 | -0.017 | 0.049 | 0.082 |
| Log sales in peak time | ||||||
| GLM -training dataset of all curves | 0.986 | -0.356 | 0.356 | -0.-001 | 0.099 | 0.144 |
| GLM -testing dataset of all curves | 0.998 | -0.114 | 0.199 | 0.004 | 0.053 | 0.096 |
| Time to reach peak sales | ||||||
| GLM -training dataset of all curves | 0.975 | -2.354 | 1.547 | -0.038 | 0.540 | 0.893 |
| GLM -testing dataset of all curves | 0.988 | -1.170 | 2.000 | 0.120 | 0.503 | 0.988 |
Abbreviations: Min E, minimum error; Max E, maximum error; ME, mean error; SD, standard deviation.
3.4. The Impact of Product-Related and Competition-Related Factors on PLC Curves
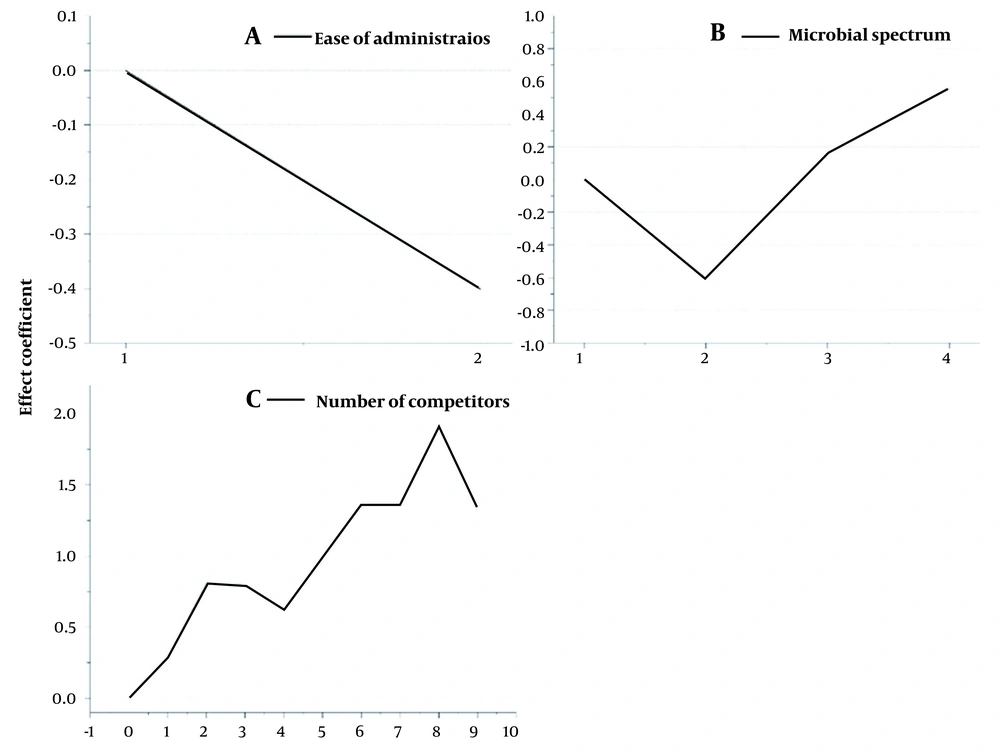
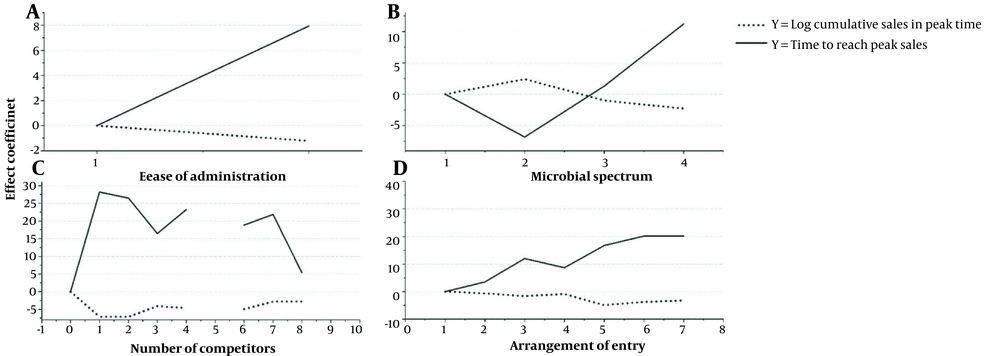
Table 3 shows the coefficient of the effects of each variable on the research objectives. Figure 3 illustrates the effect of each significant categorical variable on the PLC curves. Figure 3A shows that oral pharmaceutical forms (code 1) positively affect cumulative sales.
| Parameters | Dependent Variable = Log Cumulative Sales | Dependent Variable = Log Cumulative Sales in Peak Time | Dependent Variable = Time to Reach Peak Sales | |||
|---|---|---|---|---|---|---|
| Results for All PLC Curves | Results for PLC Curves with One Peak | |||||
| Beta | Sig. | Beta | Sig. | Beta | Sig. | |
| Intercept | 8.803 | 0.000 | 477.563 | 0.000 | -52.631 | 0.000 |
| H2 | Accepted | Accepted | Rejected | |||
| Ease of administration | - | 0.000 | - | 0.000 | - | 0.000 |
| [Ease of administration = 2] | 0.402 | 0.000 | -1.217 | 0.000 | 7.944 | 0.000 |
| [Ease of administration = 1] | 0a | - | 0a | - | 0a | - |
| H3 | Accepted | Rejected | Rejected | |||
| Microbial spectrum | - | 0.000 | - | 0.000 | - | 0.000 |
| [Microbial spectrum = 4] | 0.556 | 0.203 | -2.306 | 0.000 | 11.188 | 0.000 |
| [Microbial spectrum = 3] | -0.604 | 0.000 | -0.987 | 0.000 | 1.304 | 0.140 |
| [Microbial spectrum = 2] | 0.158 | 0.125 | 2.411 | 0.000 | -6.819 | 0.000 |
| [Microbial spectrum = 1] | 0a | . | 0a | - | 0a | - |
| H5 | Rejected | Accepted | Rejected | |||
| Arrangement of entry | - | 0.595 | - | 0.000 | - | 0.000 |
| [Arrangement of entry = 7] | 0.781 | 0.082 | -3.198 | 0.000 | 20.111 | 0.000 |
| [Arrangement of entry = 6] | -0.170 | 0.648 | -3.795 | 0.000 | 20.111 | 0.000 |
| [Arrangement of entry = 5] | 0.033 | 0.894 | -4.890 | 0.000 | 36.694 | 0.000 |
| [Arrangement of entry = 4] | -0.009 | 0.959 | -0.910 | 0.007 | 8.726 | 0.000 |
| [Arrangement of entry = 3] | 0.095 | 0.578 | -1.639 | 0.000 | 12.052 | 0.000 |
| [Arrangement of entry = 2] | -0.080 | 0.639 | -0.617 | 0.007 | 3.499 | 0.012 |
| [Arrangement of entry = 1] | 0a | - | 0a | - | 0a | - |
| H4 | Rejected | Accepted | Rejected | |||
| Number of competitors | - | 0.000 | - | 0.000 | - | 0.000 |
| [Number of competitors = 8] | 1.332 | 0.000 | -2.777 | 0.000 | 5.449 | 0.039 |
| [Number of competitors = 7] | 1.907 | 0.000 | -2.806 | 0.000 | 21.856 | 0.000 |
| [Number of competitors = 6] | 1.357 | 0.000 | -4.971 | 0.000 | 18.820 | 0.000 |
| [Number of competitors = 5] | 0.992 | 0.000 | - | - | - | - |
| [Number of competitors = 4] | 0.622 | 0.001 | -4.633 | 0.000 | 23.196 | 0.000 |
| [Number of competitors = 3] | 0.795 | 0.000 | -4.103 | 0.000 | 16.422 | 0.000 |
| [Number of competitors = 2] | 0.808 | 0.000 | -7.113 | 0.000 | 26.452 | 0.000 |
| [Number of competitors = 1] | 0.284 | 0.065 | -7.132 | 0.000 | 28.152 | 0.000 |
| [Number of competitors = 0] | 0a | - | 0a | - | 0a | - |
| H1 | Accepted | Accepted | Rejected | |||
| Quality | 0.664 | 0.000 | 7.807 | 0.000 | -21.583 | 0.000 |
| Time to peak | - | - | 0.112 | 0.000 | - | 0.000 |
Figure 3B indicates that antibiotics in spectrum category 2 (see method section) have less cumulative sales than spectrum category 1. However, broad-spectrum antibiotics (categories 3 and 4) have more cumulative sales than narrow-spectrum drugs.
Figure 3C reveals the effect of the number of competitors on cumulative sales. In contrast to expectations, the general trend of this chart was positive. In other words, the number of competitors was positively correlated with the cumulative sales of each manufacturer's medicines. This is probably because the total demand raised with increased domestic manufacturers over time. However, the relationship between the two variables was reversed when the number of competitors exceeded eight. Moreover, according to Table 3, there was a positive connection between quality and cumulative sales.
3.5. The Impact of Product-Related and Competition-Related Factors on One-Peak PLC Curves
For the one-peak PLC curves, quality, microbial spectrum, the number of competitors, time to reach peak sales, and entry arrangement significantly affected sales in the peak (the highest point of the PLC curves); however, quality, microbial spectrum, the number of competitors, and entry arrangement significantly affected the time to reach peak sales as well (Table 3).
Figure 4 shows the effect of the main variables on the sales at the peak and the time to reach peak sales in the one-peak PLC curves. Graph A demonstrates that fewer sales are recorded in the peak time in injectable (code 2) than in oral (solid-line) forms. Moreover, according to the dot-line in graph A, the injectable forms reached sales peak later and had a more prolonged growth stage of PLC compared to the oral forms of antibiotics.
Figure 4B shows fewer peak time sales of broad-spectrum antibiotics (categories 3 and 4) and more peak time sales of narrower spectrum antibiotics (category 2) than antibiotics with spectrum category 1. The opposite was observed concerning the time to reach peak sales. Accordingly, in the one-peak PLC curves, antibiotics with spectrum category 2 had a shorter growth stage with higher peak sales than other categories.
Figure 4C illustrates the competition effect in the one-peak PLC curves. According to the results, the peak height of the producer was higher when there was no competitor. Nonetheless, this graph (like Figure 4C) indicates that when the number of competitors is > 1, more peak sales are recorded, probably due to increased demand. Concerning the time to reach peak sales, the situation is vice versa: the early entrant gets peak sales sooner (hence, shorter growth phase) than later entrants with a more competitive market. Moreover, the effect of adding one competitor in the market was extremely high, and then the addition of newer competitors would have a more negligible effect.
Figure 4D shows the effect of the order of entry on the PLC curves. As presented, later entrants gained fewer peak sales than the early entrants. Moreover, these producers reached peak sales later than the early entrants. Further, drugs with higher quality got more peak sales and reached peak sales sooner.
In all these graphs, there is an inverse relationship between the trajectory of the height peak and the time to reach the peak, indicating that more peak sales are associated with the shorter growth phase of the product life cycle.
4. Discussion
We collected the sales data of 261 oral and injectable forms of systemic antibiotics having more than ten years of presence in the market. More than half of the studied PLCs had oscillating sales patterns during 2001 - 2017; hence, we could not judge their PLC stage position according to the product life cycle concept. One of the critical limitations of the PLC theory is that it describes a specific stage for products only based on the sale variable (41). Pharmaceutical products usually have an oscillating sales pattern due to various factors, some of which are addressed in this study. However, we can identify the PLC stage based on the PLC curves and sales growth for other patterns with a more transparent shape. The medicines with positive slope and linear sales graphs stayed in the growth stage for more than ten years, and these medicines could well maintain their market (n = 10). For PLCs with polynomial and positive slope (binomial equations), they were not in the decline stage because, as presented in the graphs, their sales growth stopped or was slightly incremental. The one-peak sales pattern showed the decline stage of PLC. The analysis of the one-peak sales curves showed that the range of the time-lapse to peak arrival was 2 - 14 years, and the average of this variable was 7.3 years in PLC. Two other patterns (linear and binominal with negative slope) were losing their market during the study time, and these medicines were in the decline stage from 2002 to 2017 regarding their PLCs.
According to the GLM results, the area under curves of the antibiotics (cumulative sales) depended on the quality, ease of administration, microbial spectrum, and the number of competitors. Most of these findings are consistent with previous studies (5, 18, 22). We found a positive relationship between competitors and cumulative sales concerning the competition factor in all curves. The increasing demand for antibiotics can explain this unexpected result. In recent years, antibiotics consumption have increased due to population growth and the irrational use of antibiotics in Iran (13); hence, the increased demand and domestic producers emerged simultaneously. This aroused the positive correlation between these two variables.
Concerning the one-peak curves, entry arrangement, quality, ease of administration, microbial spectrum, and the number of competitors had effects on peak sales and the time to reach peak sales. In some cases, our findings are consistent with Fisher's study (18), suggesting that the later entrants gain fewer sales in the peak time (based on GLM) and less market share (based on correlation results) than early entrants. However, concerning the time to reach peak sales, the present findings show that early entrants reach the peak sales sooner than later entrants, which is in contrast with Fisher's findings. Moreover, the higher competitive environment was generally correlated with higher peak sales and shorter growth phases. These findings, including those observed in all PLC curves, can be explained by further demand for antibiotics in recent years in Iran (13), encouraging more producers to enter the market, hence shortening the growth phase of PLC.
The next point is that reaching peak sales sooner in the generic pharmaceutical market may be correlated with an increase in cumulative sales during PLC. This finding contradicts Fisher's findings (18). One reason is the fundamental differences between the generic Iranian pharmaceutical market and those studied by Fisher. In Iran, there is no brand medicine, and all companies are generic or brand-generic producers. Moreover, the order of entry for the concerned antibiotics in this study is not much different from one another because, due to their generic nature, they have been produced at short-time intervals. Accordingly, in such a tight competitive environment, reaching the peak sales sooner than competitors and maintaining this peak, and probably prolonging the maturity phase of PLC are competitive advantages helping manufacturers gain more market share.
Finally, it should be noted that the analyses in the present study are based on the sales data, not on the defined daily dose (DDD); therefore, all the findings are from the manufacturers' perspectives. We mainly focused on sales trends and patterns to examine the PLC theory regarding the scope of the present study. Considering the DDD instead of digital sales in future studies is recommended. Due to the lack of daily or monthly sales data, we included that annual information about antibiotics sales as such the accuracy of our findings in analyzing PLC may decrease. Future researchers can avoid this issue by adding further information.