1. Background
Osteoporosis is a systemic skeletal disease characterized by decreased bone density and impairment in bone tissue microarchitecture, causing more fragile bones and a greater likelihood of fractures (1). Osteoporosis is a common public health problem worldwide, and it depends on many factors, such as ethnicity, gender, age, nutritional status, drug use, and diseases affecting bone density (1, 2). Osteoporosis and osteoporotic fractures have undesirable consequences on the individual and society in terms of financial, psychosocial, physical, and quality of life aspects (1, 2). This is why early diagnosis of osteoporosis, especially before the development of fractures, is essential.
World Health Organization (WHO) adopted the bone mineral density (BMD) test with dual-energy X-ray absorptiometry (DEXA) as a reference standard in 1994 (3). The T-score, which reflects how much standard deviation (SD) above or below the mean BMD of a young, healthy white woman, is used by WHO to identify osteoporosis. When the T-score is -2.5 SD or less, osteoporosis is diagnosed (2). While DEXA is economical and non-invasive, it has low sensitivity to predict fractures and involves low-dose ionizing radiation (4, 5). Furthermore, it has some limitations, such as the possibility that reference data for BMD provided by manufacturers may not be appropriate for local populations, being affected by body size, osteodegenerative changes, vascular calcifications, prior injected contrast media, fractures and deformities, two-dimensional measurement of BMD, and operator dependency (4, 6). Other imaging modalities such as quantitative computed tomography (QCT), quantitative ultrasound (QUS), and high-resolution peripheral quantitative computed tomography (HR-pQCT) emerged as a probable alternative to DEXA. Quantitative computed tomography provides 3D imaging and accurate bone density measurements but is limited by higher radiation doses and costs. Quantitative computed tomography is portable and radiation-free, suitable for screening but less accurate than DEXA and QCT. High-Resolution peripheral quantitative computed tomography offers detailed bone microarchitecture assessment, improving fracture prediction and monitoring therapy, but its use is restricted by high costs and limited availability (7-9).
Many studies in the literature have evaluated and demonstrated the use of various magnetic resonance imaging (MRI) techniques in the diagnosis of osteoporosis. In osteoporotic bone, the proportion of adipose tissue increases as bone production declines, which is thought to be caused by the differentiation of stromal cells into adipocytes rather than osteoblasts (10, 11). The amount of fat, protein, water, and bone cells determines how the bone marrow appears on the MRI sequence (5, 12-20). Among these studies, the apparent diffusion coefficient (ADC) values decreased in osteoporotic patients, which was hypothesized to be related to a decrease in diffusion due to the narrowing of the extracellular space as a result of increasing adipose tissue (5, 12, 15, 16, 19, 20). Apparent diffusion coefficient denotes a biological tissue's particular diffusion capacity, microscopic structure, and organization (21).
Radiomics and machine learning (ML) offer novel approaches for osteoporosis diagnosis by extracting high-dimensional data from medical images, which traditional methods might overlook. Radiomics can quantify tissue heterogeneity and capture subtle changes in bone microarchitecture, while ML algorithms can analyze these complex data sets to identify patterns indicative of osteoporosis (14, 17, 22, 23). These techniques could complement existing diagnostic methods, such as DEXA, by providing more detailed and accurate assessments of bone health (22). Early and accurate detection of osteoporosis using these advanced techniques could potentially lead to better clinical outcomes by enabling timely intervention and personalized treatment plans, thus reducing the risk of fractures and associated complications.
2. Objectives
The primary objective of this study is to evaluate the diagnostic performance of various ML models, specifically naive bayes and neural networks, in identifying osteoporosis using radiomics features extracted from lumbar MRI ADC maps. This will be measured using performance metrics such as AUC, accuracy, sensitivity, specificity, F1 score, and recall. Additionally, the secondary objective is to identify the most significant radiomics features that contribute to accurate osteoporosis diagnosis. The hypotheses guiding this study are: (1) machine learning models can significantly improve the diagnostic accuracy of osteoporosis compared to traditional methods; and (2) specific radiomics features from lumbar MRI ADC maps are significantly associated with osteoporosis and can reliably differentiate between osteoporotic and non-osteoporotic cases. These objectives and hypotheses are designed to provide a comprehensive evaluation of the potential of ML in enhancing osteoporosis diagnosis, with a focus on both model performance and feature significance.
3. Patients and Methods
3.1. Study Design and Patient Selection
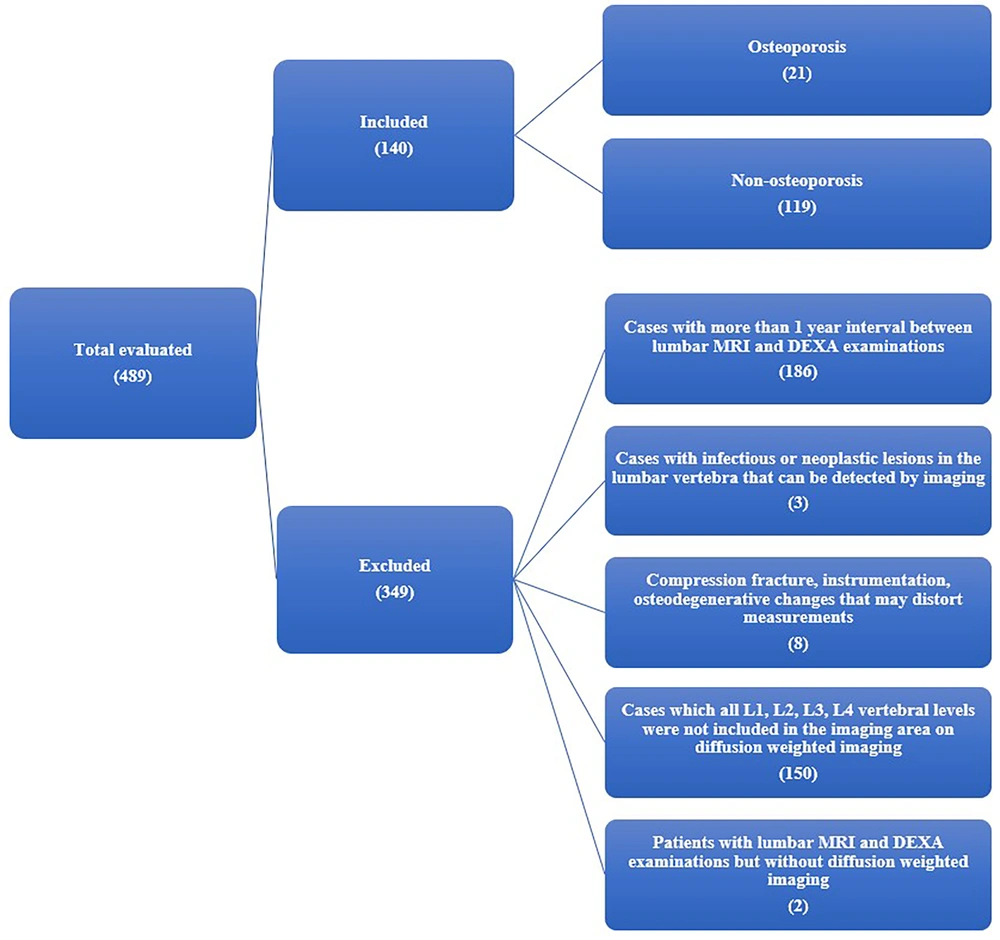
This cross-sectional study retrospectively scanned cases referred to the Radiology Department between 01/01/2015 and 31/12/2020. Lumbar MRIs were obtained from a Philips Ingenia 1.5T MRI system (Philips, Best, Netherlands), and BMD measurements were acquired using a DEXA device (Lunar Prodigy, model 8743; GE Lunar, Madison, WI, USA). Lumbar MRIs and DEXA examinations from the same patients, performed within one year of each other, were included unless they met the exclusion criteria.
Exclusion criteria were as follows:
(1) Interval exceeding one year between lumbar MRI and DEXA examinations,
(2) Presence of an infectious or neoplastic lesion in any lumbar vertebral body,
(3) Fracture of a lumbar vertebral body, instrumentation, or osteodegenerative changes that could impair the measurements,
(4) Cases in which the first four lumbar vertebrae were not included in the imaging field,
(5) Absence of diffusion-weighted imaging.
The study continued with 140 participants, 21 of whom had osteoporosis, after exclusion (Figure 1). The cases’ height and weight were recorded. Anterior-posterior lumbar vertebrae BMD was routinely measured. The DEXA scan used L1-4 as the basis for T-scores. The cases were classified as “osteoporosis” if the T-score was ≤ -2.5, and “non-osteoporosis” if the T-score was > -2.5.
Figure 1.
Patients’ enrollment diagram
3.2. Image Acquisition
The lumbar MRI diffusion-weighted imaging sequence was acquired axially on a Philips Ingenia 1.5T MRI device (Philips, Best, Netherlands). The sequence utilized a spin-echo technique with fat suppression (SPIR) and a parallel imaging method (SENSE). The pulse repetition time was 7505 milliseconds, the echo time was 60 milliseconds, and the echo train length was 43. The slice thickness was 3 mm, with a 3 mm gap between slices. the field of view (FOV) was 225 × 225 mm², and the b-values were 0 and 650 s/mm².
The PACS software available in our hospital was used as the archiving system. Lumbar MRI diffusion-weighted images (b-values of 0 and 650 s/mm²) of the cases that met the criteria were transferred to the 3DSlicer 4.8.1 program in DICOM (Digital Imaging and Communications in Medicine) format. First, monoexponential ADC maps were created with the module named DWModeling.
3.3. Segmentation
Segmentation was performed manually by an experienced board-certified radiologist. To ensure consistency, the intraobserver reliability was evaluated using the intraclass correlation coefficient (ICC), which measured the absolute agreement between the features obtained from two separate segmentation sets performed at a one-month interval. Features that achieved good (0.75 ≤ ICC < 0.9) to excellent (ICC ≥ 0.9) intraobserver reliability were considered stable.
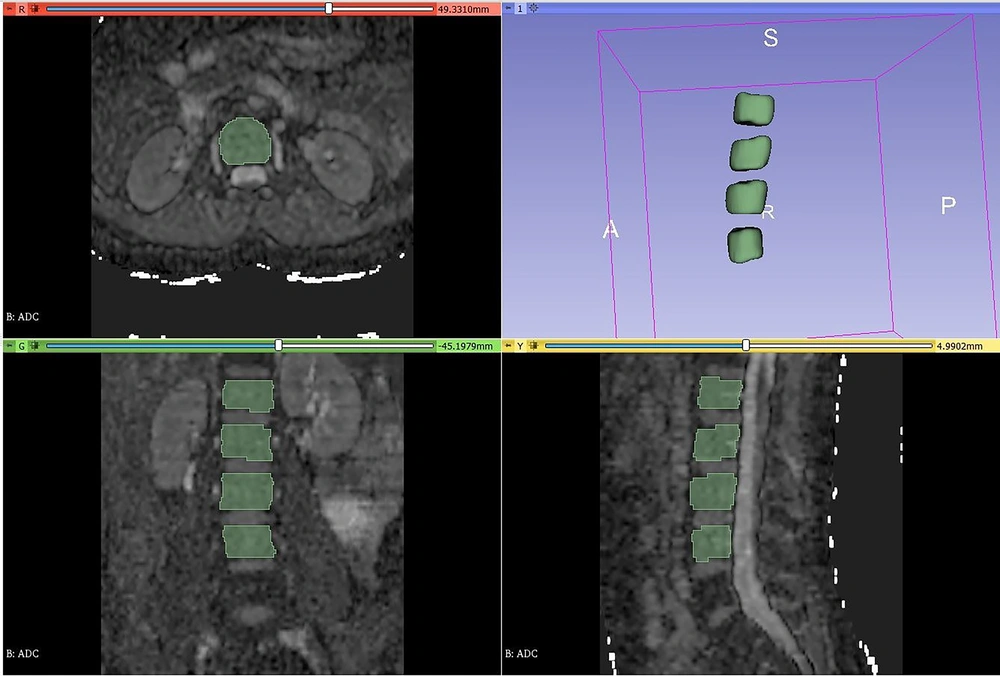
The contours were meticulously drawn to closely follow the cortical bone while remaining within the boundaries of the vertebral body. Each vertebral level was segmented separately and named as L1, L2, L3, and L4. Additionally, inspired by the DEXA assessment, which provides average bone mineral density values for L1, L2, L3, and L4 levels, the segmentations were combined into two separate sets: L1-4 and L2-4. Consequently, a total of six segmentations—L1, L2, L3, L4, L1-4, and L2-4—were obtained for each case (Figure 2).
Figure 2.
Segmentation process on 3D Slicer software of lumbar vertebrae
3.4. Preprocessing and Radiomics Feature Extraction
Following the segmentation process, features were extracted from segmented volumes using the PyRadiomics-based Radiomics module. Prior to feature extraction, a consistent configuration was applied across all cases. Specifically, under the module’s “resampling and filtering” section, the bin width was fixed at 25. Additionally, the Laplacian of gaussian filter kernel size was set to 3 mm, and wavelet-based features were enabled to generate transformed filtered images. This standardization aimed to achieve uniformity among cases, increase the volume of data, and capture high dimensionality in the radiomics dataset.
Subsequently, for each of the L1, L2, L3, L4, L1-4, and L2-4 segmentations, the following features were extracted:
- First-order features (18 features) from the original images
- Second-order features based on gray level co-occurrence matrix (GLCM) (24 features)
- Second-order features based on gray level dependence matrix (GLDM) (14 features)
- High-order features based on gray level run length matrix (GLRLM) (16 features)
- High-order features based on gray level size zone matrix (GLSZM) (16 features)
- High-order features based on neighborhood gray-tone difference matrix (NGTDM) (10 features)
Additionally, features were extracted from Laplacian of Gaussian-filtered images with a kernel size of 3 mm:
- First-order features (18 features)
- Second-order features based on GLCM (24 features)
- Second-order features based on GLDM (9 features)
- High-order features based on GLRLM (16 features)
- High-order features based on GLSZM (16 features)
- High-order features based on NGTDM (5 features)
Furthermore, a total of 744 features were obtained from wavelet-transformed images for each case, resulting in a grand total of 5,580 features across all cases.
3.5. Feature Selection, Model Validation, Classification, and Performance Evaluation
For classification using ML algorithms, the Orange data mining program version 3.30 was employed. The dataset consisted of 5,580 features and 140 cases, which were subjected to classification using seven distinct ML algorithms: k-nearest neighbors (kNN), decision tree, random forest, logistic regression, support vector machine (SVM), naive bayes, and neural network. The classification was performed both before and after the feature selection process using these seven ML algorithms to evaluate the positive effect of feature selection on the performance metrics.
In this study, we used the fast correlation-based filter (FCBF) method to select five features from the extracted radiomics data. The choice of five features was based on preliminary experiments, aiming to balance the trade-off between reducing dimensionality and retaining significant predictive power. This approach helps mitigate the risk of overfitting by focusing on the most relevant features while avoiding the inclusion of redundant or less informative ones. We recognize that the optimal number of features may vary with different datasets and encourage further research to explore this aspect.
The ML models were validated using 10-fold cross-validation to ensure robust evaluation. This method involves dividing the dataset into ten equal parts, with each part used as a validation set while the remaining nine parts are used for training. This process is repeated ten times, with each part serving as the validation set once. The performance metrics were calculated by averaging the results from each fold, providing a more reliable estimate of the model's performance compared to a single train-test split.
The performance metrics, including AUC (Area Under the Curve), classification accuracy (CA), F1 score, precision (positive predictive value), recall (sensitivity), and specificity, were calculated for each fold. These metrics provide a comprehensive evaluation of the model’s diagnostic capabilities, measuring its ability to correctly identify positive and negative cases of osteoporosis. The use of cross-validation ensures that the models are not overfitted to a particular subset of the data and can generalize well to unseen data.
3.6. Conventional Statistical Analysis
IBM SPSS Statistics for Windows, version 22 (IBM Corp. Released 2013. IBM SPSS Statistics for Windows, Version 22.0. Armonk, NY: IBM Corp.), was used for conventional statistical analysis. After evaluating the ML model performance, independent samples t-test and Mann-Whitney U test were performed to determine whether each feature showed a statistically significant difference in osteoporosis status. The normal distribution of data was assessed using the Kolmogorov-Smirnov test and histogram graphs. Means and SDs for normally distributed data and medians and interquartile ranges for non-normally distributed data were expressed as mean ± SD and median (interquartile range), respectively. Categorical data were expressed as counts and percentages.
Receiver Operating Characteristic curve analysis was performed for features found to be significant in these tests, and threshold values were determined. Threshold values for significant radiomics features were established using the Youden index. The Youden index was employed to identify the optimal cut-off points that maximize the sum of sensitivity and specificity, thereby ensuring balanced and effective discrimination between osteoporotic and non-osteoporotic cases. A P-value of < 0.05 was considered significant in all statistical results.
3.7. Ethical Considerations
This study was approved by the Clinical Research Ethics Committee of Balikesir University Faculty of Medicine on 26/05/2021, with the decision number 2021/129. Informed consent was not required due to the retrospective nature of the study.
4. Results
A total of 140 cases (132 females, 8 males; mean age 65.32 ± 8.50 years) were included. For women, the mean age was 65.20 ± 8.19 years, and for men, it was 67.22 ± 13.28 years. Female subjects had a median height of 1.53 ± 0.08 m, mean body weight of 73.21 ± 13.81 kg, and mean BMI of 31.43 ± 5.53 kg/m². Male subjects had a mean height of 1.67 ± 0.08 m, mean body weight of 73.25 ± 15.64 kg, and mean BMI of 26 ± 3.59 kg/m².
Age, body weight, and BMI fit a normal distribution for all cases and by gender, except height, which was normally distributed only for males. An independent samples t-test showed no significant age difference between osteoporotic and non-osteoporotic groups (P = 0.889), but body weight and BMI were significantly different (P = 0.003 and P = 0.001, respectively). The osteoporotic group had lower mean body weight (64.90 ± 10.13 kg) and BMI (27.40 ± 4.38 kg/m²) compared to the non-osteoporotic group (74.68 ± 13.94 kg and 31.77 ± 5.52 kg/m²) (Table 1). No significant difference in height was found (P = 0.412).
Table 1.
Comparison of Age, Body Weight and Body Mass Index Between Osteoporotic and Non-osteoporotic Subjects
| Variables | Independent samples t-test (t-test for equality of means) | ||
|---|---|---|---|
| Sig. (2-tailed) | Mean difference | Std. error difference | |
| Age | 0.889 | -0.28 | 2.02 |
| Body weight (kg) | 0.003 | -9.78 | 3.18 |
| BMI (kg/m2) | 0.001 | -4.37 | 1.27 |
Abbreviation: BMI, body mass index.
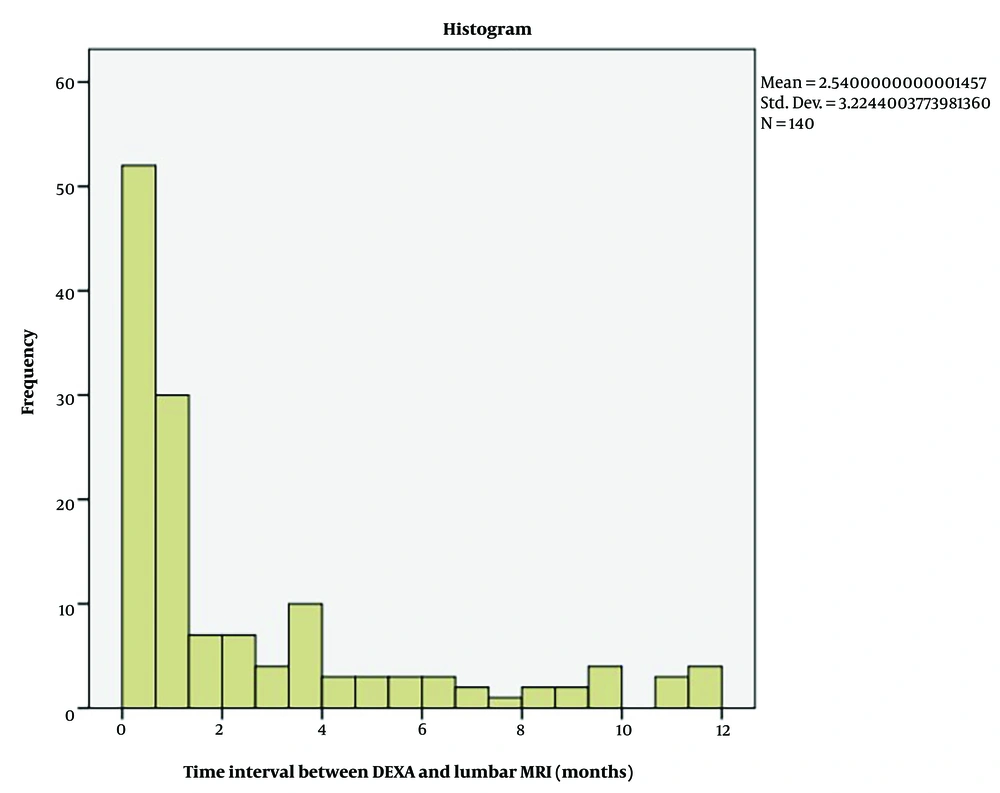
The median interval between DEXA and lumbar MRI was 1 month (max 11.87 months) (Figure 3).
Figure 3.
Histogram plot showing frequencies of time interval between dual-energy X-ray absorptiometry (DEXA) and lumbar MRI
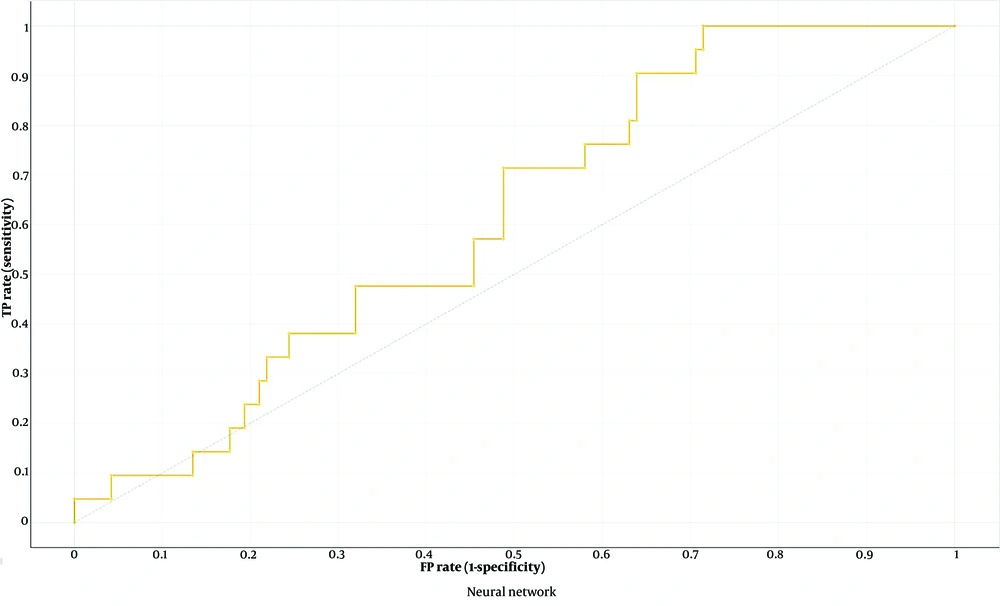
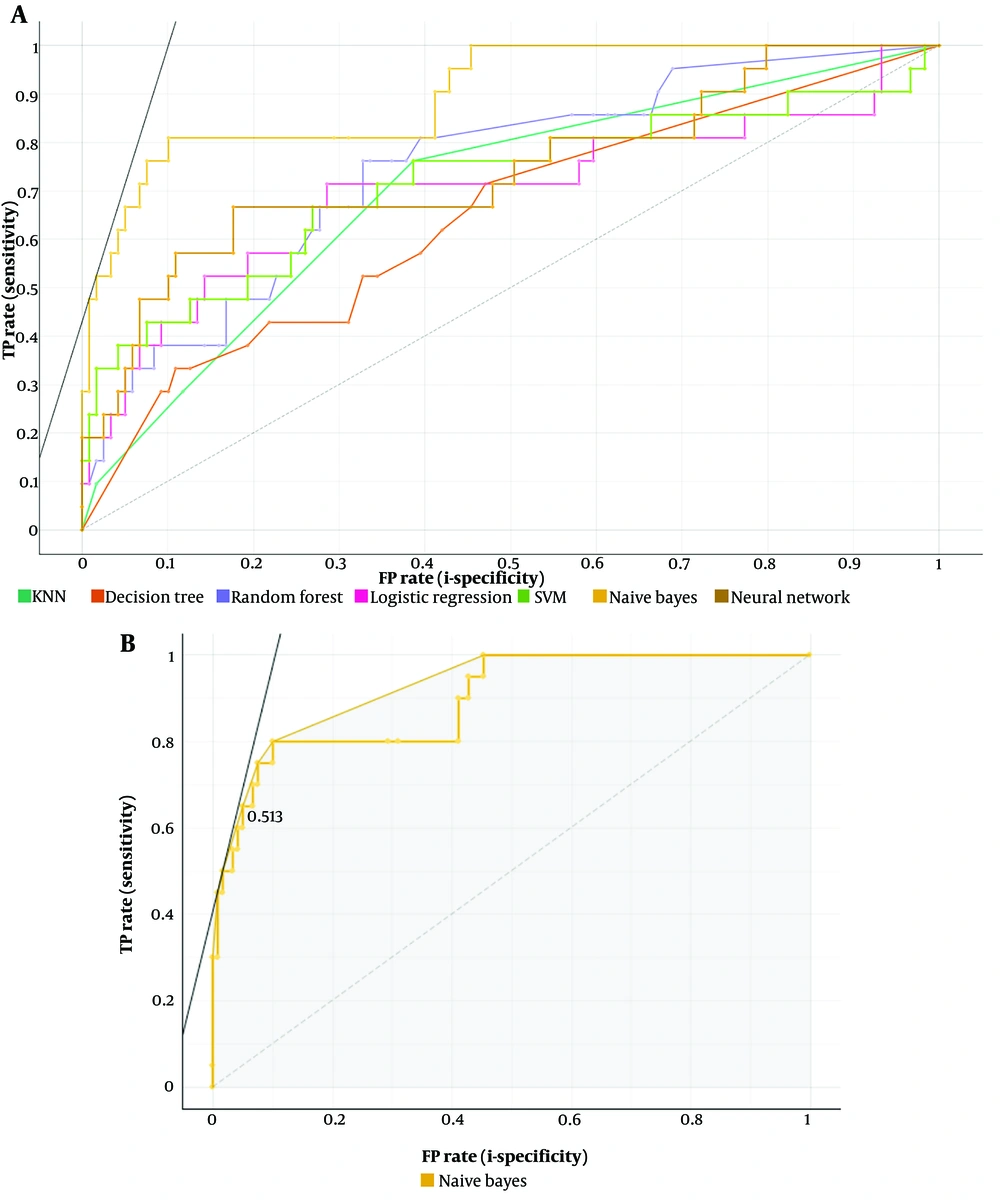
The neural network was the top-performing ML model using 5,580 radiomics features for osteoporosis detection (AUC 0.616, CA 0.764, F1 score 0.108, precision 0.125, recall 0.095, specificity 0.882) (Figure 4). Feature selection with FCBF improved performance across seven ML models (Table 2), with Naive Bayes achieving the highest performance (AUC 0.913, CA 0.907, F1 score 0.683, precision 0.7, recall 0.667, specificity 0.95) (Tables 3 , 4 and Figure 5A and B).
Figure 4.
Receiver operating characteristic (ROC) curve of the neural network model formed with all radiomics features (5580 radiomics features)
Table 2.
The Selected Five Features and their Definitions
| Radiomics feature a | Definition |
|---|---|
| L1-4 log-sigma-3-0-mm-3D GLCM sum squares | The sum of squares or Variance is a measure of the mean intensity level in the GLCM in the distribution of neighboring intensity level pairs. The L1-4 label represents the related segmented vertebral level. It was obtained from the images created by choosing the Laplacian of Gaussian filter 3 mm. |
| L3 log-sigma-3-0-mm-3D first order minimum | First order minimum is the minimum grey level value in the image. The L3 label represents the related segmented vertebral level. It was obtained from the images created by choosing the Laplacian of Gaussian filter 3 mm. |
| L3 wavelet-LLH first order Mean | First order mean is the average grey level value in the image. The L3 label represents the related segmented vertebral level. It was obtained from the images created by wavelet transform. LLH is one of the 8 sub volumes in the 3D wavelet transform. |
| L1 wavelet-LHH GLSZM large area high gray level emphasis | LAHGLE measures the ratio in the image of the co-distribution of larger sized regions with higher grey level values. The L1 label represents the related segmented vertebral level. It was obtained from images created by wavelet transform. LHH is one of the 8 sub volumes in the 3D wavelet transform. |
| L2 log-sigma-3-0-mm-3D GLCM IDN | One of the measures of an image's local homogeneity is IDN (inverse difference normalized). Unlike homogeneity1, IDN normalizes the difference in intensity values between neighbors by dividing it by the total number of discrete intensity values. The L2 label represents the related segmented vertebral level. It was obtained from the images created by choosing the Laplacian of Gaussian filter 3 mm. |
Abbreviations: GLSZM, gray level size zone matrix; GLCM, gray level co-occurrence matrix.
a The 5 features selected by fast correlation-based filter (FCBF).
Table 3.
The Performance Values of Machine Learning Models Formed with the Five Selected Features by Fast Correlation-Based Filter a
| Variables | AUC | CA | F1 | Precision | Recall | Specificity |
|---|---|---|---|---|---|---|
| ML Algorithm | ||||||
| Naive Bayes | 0.913 | 0.907 | 0.683 | 0.7 | 0.667 | 0.95 |
| Neural Network | 0.752 | 0.864 | 0.296 | 0.667 | 0.19 | 0.983 |
| Random Forest | 0.743 | 0.864 | 0.345 | 0.625 | 0.238 | 0.975 |
| SVM | 0.738 | 0.857 | 0.091 | 1 | 0.048 | 1 |
| Logistic Regression | 0.722 | 0.864 | 0.296 | 0.67 | 0.19 | 0.983 |
| kNN | 0.709 | 0.85 | 0.16 | 0.5 | 0.095 | 0.983 |
| Decision Tree | 0.654 | 0.8 | 0.333 | 0.333 | 0.333 | 0.882 |
Abbreviation: ML, machine learning; AUC, area under the curve; SVM, support vector machine; KNN, k-nearest neighbors.
a The performance of ML algorithms.
Table 4.
Confusion Matrix for the Naive Bayes Model (5 Features) a
| Variable | Predicted | ||
|---|---|---|---|
| Osteoporotic | Non-osteoporotic | Total | |
| Actual | |||
| Osteoporotic | 14 (10) | 7 (5) | 21 |
| Non-osteoporotic | 6 (4) | 113 (81) | 119 |
| Total | 20 | 120 | 140 |
a Confusion matrix for the Naive Bayes model (showing number of instances and percentages).
Figure 5.
Receiver operating characteristic (ROC) curves of the all seven ML model (A); and the Naive Bayes model only (B). (Abbreviations: kNN, k-nearest neighbors; SVM, support vector machine; ML, machine learning).
All features had ICC values > 0.75, indicating reliability. Independent samples t-test and Mann-Whitney U tests identified 521 and 670 significant features (P < 0.05) for osteoporosis status, respectively. Receiver operating characteristic (ROC) analysis showed 58 features with AUC > 0.70, predominantly from wavelet-transformed images (42 features), mainly from the LHL subvolume (30 features) and the L1 vertebra level (38 features). The Youden index determined threshold values for these features, with corresponding sensitivity and specificity provided (Table 5).
Table 5.
Threshold, Sensitivity, Specificity Values of the Radiomics Features Which had AUC Values Greater Than 0,70
| Radiomics feature | AUC (%95 CI) | P | Threshold a | Sensitivity | Specificity |
|---|---|---|---|---|---|
| L1-4 log-sigma-3-0-mm-3D first order median b | 0.742 (0.631 - 0.854) | 0.0004 | 161.8236694 | 0.714 | 0.714 |
| L1 wavelet-LHH first order range b | 0.742 (0.627 - 0.856) | 0.0004 | 772.300293 | 0.857 | 0.580 |
| L2-4 log-sigma-3-0-mm-3D first order median b | 0.74 (0.631 - 0.85) | 0.0005 | 130.8338051 | 0.905 | 0.513 |
| L1 wavelet-LHH GLDM high gray Level emphasis b | 0.733 (0.633 - 0.833) | 0.0007 | 12426.98297 | 0.762 | 0.655 |
| L1 wavelet-LHL GLDM large dependence high gray level emphasis b | 0.728 (0.623 - 0.834) | 0.0009 | 316.7002581 | 0.905 | 0.538 |
| L1 wavelet-LHL gray level size zone matrix (GLSZM) small area emphasis b | 0.726 (0.627 - 0.825) | 0.0010 | 669.0405296 | 0.857 | 0.597 |
| L1 wavelet-LHL first order minimum b | 0.726 (0.603 - 0.849) | 0.0010 | 138.3913483 | 0.667 | 0.798 |
| L4 log-sigma-3-0-mm-3D first order median b | 0.723 (0.617 - 0.829) | 0.0011 | 123.4394493 | 0.905 | 0.555 |
| L1 wavelet-LHL neighborhood gray-tone difference Matrix (NGTDM) coarseness b | 0.722 (0.623 - 0.821) | 0.0012 | 820.7429058 | 0.952 | 0.487 |
| L1 wavelet-LHL first order root mean squared b | 0.721 (0.613 - 0.829) | 0.0013 | 144355620.8 | 0.810 | 0.580 |
| L1 wavelet-HHL GLSZM zone percentage b | 0.72 (0.602 - 0.838) | 0.0013 | 0.424339815 | 0.714 | 0.723 |
| L1 wavelet-LHL first order entropy b | 0.72 (0.612 - 0.829) | 0.0013 | 594726568.4 | 0.810 | 0.580 |
| L1-4 log-sigma-3-0-mm-3D first order root mean squared b | 0.719 (0.607 - 0.831) | 0.0014 | 238.6731562 | 0.714 | 0.739 |
| L1 wavelet-LHL first order variance b | 0.719 (0.606 - 0.832) | 0.0014 | 183.7174645 | 0.952 | 0.403 |
| L1 wavelet-LHL gray level run length matrix (GLRLM) long run emphasis b | 0.719 (0.607 - 0.831) | 0.0014 | 56.88197474 | 0.952 | 0.403 |
| L1 wavelet-HHL NGTDM complexity b | 0.718 (0.6 - 0.836) | 0.0015 | 0.676536483 | 0.714 | 0.723 |
| L1 wavelet-LHL first order uniformity b | 0.718 (0.593 - 0.843) | 0.0015 | 5.645465978 | 0.571 | 0.857 |
| L1 wavelet-LHL GLRLM gray level variance b | 0.718 (0.605 - 0.831) | 0.0015 | 33487.69379 | 0.952 | 0.403 |
| L1 wavelet-LHL GLDM small dependence emphasis b | 0.718 (0.605 - 0.831) | 0.0015 | 53.66430712 | 0.952 | 0.403 |
| L1-4 log-sigma-3-0-mm-3D first order mean b | 0.718 (0.593 - 0.843) | 0.0015 | 155.6497469 | 0.762 | 0.639 |
| L1 wavelet-LHL GLRLM short run low gray level emphasis b | 0.717 (0.608 - 0.826) | 0.0015 | 2414.827911 | 0.905 | 0.471 |
| L1 wavelet-LHL GLSZM size zone non-uniformity normalized b | 0.717 (0.615 - 0.819) | 0.0015 | 893.0282637 | 0.762 | 0.664 |
| L1 wavelet-LHL GLRLM long run low gray level emphasis b | 0.717 (0.615 - 0.819) | 0.0015 | 849.1502259 | 0.762 | 0.664 |
| L1 wavelet-LHL GLDM small dependence high gray level emphasis b | 0.715 (0.614 - 0.817) | 0.0017 | 883.5853389 | 0.762 | 0.664 |
| L2 log-sigma-3-0-mm-3D first order median b | 0.715 (0.59 - 0.841) | 0.0017 | 182.5972176 | 0.619 | 0.824 |
| L3 log-sigma-3-0-mm-3D first order root mean squared b | 0.715 (0.609 - 0.821) | 0.0017 | 221.0883332 | 0.810 | 0.622 |
| L1 wavelet-HHL first order range b | 0.715 (0.603 - 0.827) | 0.0017 | 277.4433441 | 0.810 | 0.580 |
| L1 wavelet-LHL gray level co-occurrence matrix (GLCM) Id b | 0.714 (0.598 - 0.831) | 0.0018 | 74.51247581 | 0.619 | 0.723 |
| L1 wavelet-LHL GLSZM gray level non-uniformity normalized b | 0.713 (0.597 - 0.83) | 0.0018 | 5.074148459 | 0.619 | 0.782 |
| L3 log-sigma-3-0-mm-3D first order median b | 0.712 (0.601 - 0.823) | 0.0020 | 154.2673759 | 0.714 | 0.672 |
| L1-4 log-sigma-3-0-mm-3D first order 90percentile b | 0.711 (0.596 - 0.826) | 0.0021 | 374.7948471 | 0.714 | 0.748 |
| L1 wavelet-LHL first order energy b | 0.711 (0.592 - 0.83) | 0.0021 | 239.8392797 | 0.524 | 0.815 |
| L1 wavelet-LHL GLCM Imc2 b | 0.711 (0.607 - 0.815) | 0.0021 | 802.288168 | 0.762 | 0.639 |
| L1 wavelet-LHL GLCM IDM b | 0.71 (0.594 - 0.826) | 0.0022 | 90.46296759 | 0.619 | 0.731 |
| L2-4 log-sigma-3-0-mm-3D first order root mean squared b | 0.709 (0.601 - 0.818) | 0.0023 | 226.992795 | 0.714 | 0.681 |
| L3 log-sigma-3-0-mm-3D NGTDM busyness c | 0.709 (0.604 - 0.814) | 0.0023 | 0.368800857 | 0.905 | 0.471 |
| L2-4 log-sigma-3-0-mm-3D first order mean b | 0.708 (0.586 - 0.83) | 0.0024 | 145.8226851 | 0.762 | 0.588 |
| L1 wavelet-LHL first order kurtosis c | 0.707 (0.601 - 0.814) | 0.0025 | -640.053894 | 0.762 | 0.622 |
| L1 wavelet-HHL GLCM Cluster prominence c | 0.707 (0.604 - 0.81) | 0.0025 | 0.093677529 | 0.857 | 0.529 |
| L1 wavelet-LHL GLSZM Small Area high gray level emphasis c | 0.707 (0.592 - 0.821) | 0.0026 | 0.04102843 | 0.905 | 0.471 |
| L1 wavelet-LHL first order mean b | 0.706 (0.584 - 0.829) | 0.0026 | 4.713948691 | 0.571 | 0.807 |
| L1 wavelet-LHL GLCM IDMN b | 0.706 (0.601 - 0.811) | 0.0026 | 27.3785354 | 0.762 | 0.622 |
| L1 wavelet-LHL GLCM joint energy b | 0.706 (0.601 - 0.811) | 0.0026 | 54.75707079 | 0.762 | 0.622 |
| L1 wavelet-LHL GLRLM run length non-uniformity normalized b | 0.706 (0.603 - 0.809) | 0.0026 | 831.1979223 | 0.952 | 0.454 |
| L1 wavelet-LHL GLCM sum entropy b | 0.705 (0.59 - 0.821) | 0.0028 | 47.99747138 | 0.714 | 0.605 |
| L1 wavelet-HHL GLCM joint average c | 0.705 (0.585 - 0.824) | 0.0028 | 0.140912352 | 0.762 | 0.639 |
| L3 wavelet-LLH first order median b | 0.704 (0.565 - 0.843) | 0.0029 | 70.33731461 | 0.571 | 0.815 |
| L1 wavelet-LHL GLCM cluster tendency b | 0.704 (0.591 - 0.817) | 0.0029 | 575635.1876 | 0.810 | 0.571 |
| L1 wavelet-LHL first order range b | 0.703 (0.587 - 0.82) | 0.0030 | 2222.682983 | 0.571 | 0.773 |
| L2 wavelet-LLL GLCM difference average b | 0.703 (0.613 - 0.793) | 0.0031 | 18.4495188 | 1.000 | 0.479 |
| L2 log-sigma-3-0-mm-3D GLSZM zone variance c | 0.703 (0.597 - 0.809) | 0.0031 | 45.36158539 | 0.714 | 0.647 |
| L1 wavelet-LHL GLCM correlation b | 0.702 (0.579 - 0.825) | 0.0032 | 3.771944675 | 0.667 | 0.723 |
| L2 log-sigma-3-0-mm-3D GLSZM large area emphasis c | 0.702 (0.596 - 0.807) | 0.0032 | 101.9358356 | 1.000 | 0.370 |
| L1-4 wavelet-LLL GLCM difference variance b | 0.702 (0.599 - 0.805) | 0.0032 | 259.307057 | 0.857 | 0.529 |
| L3 log-sigma-3-0-mm-3D first order 90percentile b | 0.702 (0.594 - 0.809) | 0.0032 | 362.6814285 | 0.714 | 0.731 |
| L2 wavelet-LLL GLCM contrast b | 0.701 (0.611 - 0.792) | 0.0033 | 619.6491217 | 0.952 | 0.521 |
| L1 wavelet-LLL GLDM high gray level emphasis b | 0.701 (0.591 - 0.81) | 0.0034 | 269.6090191 | 0.857 | 0.504 |
| L2-4 log-sigma-3-0-mm-3D first order 90 percentile b | 0.7 (0.589 - 0.811) | 0.0035 | 357.1382874 | 0.762 | 0.681 |
a Threshold values are defined by Youden Index.
b Larger test result indicates more positive test.
c Smaller test result indicates more positive test.
Among these 58 features, 30 belonged to the L1 vertebra level and were obtained from images created by wavelet transformation. Of these 30 features, 9 were first-order, 8 were GLCM-based, 3 were GLDM-based, 5 were GLRLM-based, 4 were GLSZM-based, and 1 was NGTDM-based.
5. Discussion
Our study is the only study to predict osteoporosis using radiomics features obtained from lumbar MRI ADC maps and ML algorithms. Additionally, it is the only study that examines whether each of these radiomics features shows a statistically significant difference in osteoporosis, aiming to find a threshold value for those that show significant differences.
The neural network model demonstrated low performance metrics, including an AUC of 0.616, an F1 score of 0.108, and a recall of 0.095, despite being identified as the best model when utilizing all features. Several factors may explain this outcome. Firstly, the significant class imbalance in the dataset likely biased the model toward the majority class, impairing its ability to accurately predict the minority class. Secondly, the small dataset size limited the model's capacity to generalize and effectively learn from the data. Neural networks typically require large volumes of data to achieve optimal performance, and the lack of sufficient data may have hindered the model's efficacy. Additionally, the complexity of neural networks means they are highly sensitive to hyperparameter settings, and inadequate tuning could result in suboptimal model configurations.
Moreover, the model might have been prone to overfitting due to the high dimensionality of the feature set and the relatively small sample size. Overfitting occurs when the model learns noise and details from the training data to an extent that negatively impacts its performance on new, unseen data. This can be particularly problematic in complex models like neural networks, which have a high capacity to fit the training data too closely. These findings highlight the importance of addressing class imbalance, ensuring sufficient data volume, performing rigorous hyperparameter optimization, and implementing techniques to prevent overfitting in future studies to enhance the predictive performance of neural networks in similar applications.
The Naive Bayes model showed significant improvement after feature selection, achieving an AUC of 0.913. This improvement can be attributed to several factors. Feature selection likely removed irrelevant or redundant features, reducing the dimensionality of the data and allowing the model to focus on the most informative variables. This process enhances the model's ability to generalize from the training data to new, unseen data by minimizing the risk of overfitting.
In the clinical context, this improvement is particularly relevant. A higher AUC indicates a better ability of the model to distinguish between osteoporotic and non-osteoporotic cases, which is crucial for early diagnosis and intervention. By identifying the most significant features, clinicians can better understand the underlying factors contributing to osteoporosis, leading to more targeted and effective treatment strategies. Additionally, the use of a more accurate model in clinical practice can improve patient outcomes by enabling more precise and reliable diagnostic processes. Thus, the feature selection process not only enhances the performance of the Naive Bayes model but also has meaningful implications for improving the clinical management of osteoporosis. Future studies should continue to explore and validate these selected features to ensure their robustness and relevance in diverse patient populations.
To our knowledge, there are few studies on osteoporosis prediction using ML and radiomics data obtained from DEXA, MRI, and CT. In the study by Rastegar et al., which included 147 cases and aimed to differentiate osteoporotic, osteopenic, and normal BMD using ML models based on radiomics data from DEXA, the most successful combinations showed AUC values of 0.78 and 0.76 for the trochanteric and femoral neck regions, respectively, in differentiating osteoporosis from normal cases (22). In the study by Lim et al., a success rate exceeding 93% (CA, specificity, and negative predictive values) was achieved in predicting femoral osteoporosis using radiomics data from abdominopelvic CTs and ML algorithms (24).
In the study by He et al., which included 109 cases, radiomics data from lumbar MRI T1 and T2-weighted images and ML algorithms were utilized. AUC values for models created with data from T1-weighted images, T2-weighted images, and both were 0.772, 0.772, and 0.810, respectively, for differentiating normal from osteopenia; 0.724, 0.682, and 0.797 for differentiating normal from osteoporosis; and 0.730, 0.734, and 0.769 for differentiating osteopenia from osteoporosis (14). While BMD values were categorized as osteoporosis, osteopenia, and normal in some of these studies, the diagnostic performance of the Naive Bayes model in our study was higher for differentiating osteoporosis (Table 3).
Recent studies have also explored automated techniques. An automated method was described for detecting early-stage osteoporosis using cortical radiogram metric measures and trabecular texture analysis from hand and wrist radiographs (25). Zhao et al. developed a fully automated radiomics pipeline with deep learning-based segmentation using the DIXON sequence at six echo times with a short TE time in the lumbar region to demonstrate osteoporosis and abnormal bone density. They reported a model with success comparable to manual segmentation for BMD classification (26).
In the literature, some studies have used data obtained from CT, dental panoramic radiography, and radiographs to predict osteoporosis using deep learning algorithms, beyond classical ML approaches (27-31). Dai et al. demonstrated that BMD values from DEXA could be estimated by a model created with radiomics data from abdominal CT (32).
In the study by Burian et al., texture analysis was performed using classical statistical methods on chemical shift images to examine differences in bone marrow between pre- and postmenopausal women, with a focus on the proton density fat fraction (17). Additionally, various studies using deep learning and ML have investigated bone properties (29, 33).
There are also studies focused on detecting or predicting vertebral fractures. In a study by Ramos et al. involving 47 patients, the new ML model BEAUT (BonE Analysis Using Texture), developed using radiomics features from lumbar MRI T2-weighted images, was more effective at predicting fragility fractures than other ML models (CA 0.92, AUC 0.97) (34). In another study by Valentinitsch et al., a model combining three-dimensional texture features with regional volumetric BMD of the entire thoracolumbar spine showed high discrimination performance in detecting vertebral fractures, outperforming the diagnostic success of volumetric BMD alone (35).
Similar to our findings, numerous publications have described the relationship between low BMD, BMI, and body weight (36-40). In our study, the height and age variables did not show a significant difference in the osteoporotic group (P > 0.05). In the study by Ozeraitiene and Butenaite, it was noted that anthropometric measurements such as body weight, BMI, and skinfold thickness were lower in cases of osteoporosis (41). In the study by Mikula et al., prospective stature shortening was found to be an effective method for identifying patients with vertebral fractures, vitamin D deficiency, and low BMD. While the absence of stature shortening does not exclude these diagnoses, its presence supports a high positive likelihood ratio (42).
In the review by Yedavally-Yellayi et al., it is stated that significant stature shortening in men and women aged 50 and over is a risk factor warranting vertebral imaging (43). Advanced age is a well-known risk factor for low BMD (1, 2, 43). The high mean age of the patients in our study may explain the lack of a statistically significant age difference between the osteoporotic and non-osteoporotic groups (mean 65.32, standard deviation 8.50).
The statistically significant differences in body weight and BMI between the osteoporotic and non-osteoporotic groups are noteworthy. These factors could potentially influence the radiomics features extracted from MRI images, as body composition might affect tissue properties and, consequently, the radiomics signatures. Differences in body weight and BMI might also impact the performance of machine learning models by introducing bias related to these physical attributes. To mitigate these potential influences, future studies could consider using Z-scores for body weight and BMI, standardizing these variables relative to the population mean and standard deviation. This approach could help minimize the impact of body composition differences on radiomics feature extraction and model performance. Additionally, including body weight and BMI as covariates in the analysis could provide more robust results, ensuring that the observed differences are not solely attributable to these factors.
Selecting five features using the FCBF method effectively reduced the dimensionality of the dataset while retaining the most relevant predictive information. This decision was based on preliminary analyses, which suggested that this number provided a good balance between model complexity and performance. While this approach reduces the risk of overfitting, it is essential to validate these findings with larger datasets. Future studies should explore the impact of selecting different numbers of features on model performance and generalizability to ensure optimal outcomes.
Apart from the retrospective nature of our study, there were some limitations. One significant limitation is the low number of male cases, with only 8 male participants out of a total of 140 cases. This gender imbalance reflects the higher prevalence of osteoporosis in women but poses a challenge for the generalizability of our findings. The predominance of female cases may limit the applicability of our results to the male population, which could exhibit different patterns and responses to osteoporosis. Future studies should aim to include a larger and more balanced sample size with more male participants to ensure that the findings are generalizable to both genders. This approach would enhance the robustness and applicability of the results across different demographics.
Instead of the hold-out cross-validation, the stratified 10-fold cross-validation technique was preferred, as the number of cases was limited, and the use of hold-out cross-validation would further reduce the dataset size. The lack of external validation with an independent dataset is another important limitation. Although the maximum one-year interval between the two examinations was set as an inclusion criterion and might seem relatively long, statistical analysis of the interval showed that DEXA and MRI examinations were frequently taken at close intervals (median difference of 1 month, with an interquartile range of 3.44 months).
In conclusion, we defined an ML model with good performance in the diagnosis of osteoporosis by using radiomics features obtained from lumbar MRI ADC maps. We also determined the threshold values at which each radiomics feature performed optimally. In the future, larger-scale prospective studies with a balanced male-to-female ratio and the use of ML and radiomics data from multiparametric MRI sequences could be transformative in diagnosing osteoporosis.
