Comparison of Different Approaches in Estimating Initial Reproduction Number of SARS-CoV-2 in the Islamic Republic of Iran

Nasrin Talkhi; Nayereh Esmaeilzadeh; Mohammad Taghi  Shakeri; Zahra Pasdar

doi:10.5812/jamm.113224

Journal of Archives in Military Medicine

JAMM International

Home

Current Issue All Issues In Press Articles Search Accepted Manuscripts

Instructions

Journal Information Board and Committees Indexing and Listing Sources Journal Metrics Publication Ethics and Malpractice Statement Support Reviewer and AE Registration Form Contact Us Open Peer Review (OPR)

Authors Guide Submit Manuscript

Image Credit:J Arch Mil Med

https://doi.org/10.5812/jamm.113224

Comparison of Different Approaches in Estimating Initial Reproduction Number of SARS-CoV-2 in the Islamic Republic of Iran

Author(s):

Nasrin Talkhi ¹,

Nayereh Esmaeilzadeh

²,

Mohammad Taghi Shakeri

^1,*,

Zahra Pasdar

1Department of Biostatistics, School of Health, Mashhad University of Medical Sciences, Mashhad, Iran

2Department of Epidemiology, School of Health, Mashhad University of Medical Sciences, Mashhad, Iran

3Institute of Applied Health Sciences, School of Medicine, Medical Sciences and Nutrition, University of Aberdeen

Journal of Archives in Military Medicine:Vol. 9, issue 2; e113224

Published online:Apr 21, 2021

Article type:Research Article

Received:Feb 11, 2021

Accepted:Mar 13, 2021

How to Cite:Talkhi N, Esmaeilzadeh N, Shakeri MT, Pasdar Z. Comparison of Different Approaches in Estimating Initial Reproduction Number of SARS-CoV-2 in the Islamic Republic of Iran. J Arch Mil Med. 2021;9(2):e113224. doi: https://doi.org/10.5812/jamm.113224

Abstract

Background:

The basic reproduction number (R0) is an epidemic threshold parameter that indicates the magnitude of disease transmission and thus allows suggestions for the planning of control measures.

Objectives:

Our aim in this study was to compare different approaches for estimating R0 in the early stage of the SARS-CoV-2 outbreak and discern the best-fitting model.

Methods:

The dataset was derived from cumulative laboratory-confirmed COVID-19 cases from 26th February to 30th May 2020 in Iran. The methods of exponential growth (EG) rate, maximum likelihood (ML), time-dependent (TD) reproduction number, attack rate (AR), and sequential Bayesian (SB) model were used. The gamma distribution (mean 4.41 ± 3.17 days) was used for serial interval (SI) distribution. The best-fitting method was selected according to the lowest root mean square error (RMSE).

Results:

We obtained the following estimated R0 [95% confidence interval]: 1.55 [1.54; 1.55], 1.46 [1.45; 1.46], 1.31 [1.30; 1.32], and 1.40 [1.39; 1.41] using EG, ML, TD, and SB methods, respectively. Additionally, the EG and ML methods showed an overestimation of R0, and the SB method showed to be under-fitting in the estimation of R0. The AR method estimated R0 equal to one. The TD method had the lowest RMSE.

Conclusions:

The simulated and actual R0 of TD showed that this method had a good fit for actual data and the lowest RMSE. Therefore, the TD method is the most appropriate method with the best performance in estimating actual R0 values.

Keywords

COVID-19

Initial Reproduction Number

Exponential Growth Rate

Maximum Likelihood

Attack Rate

Sequential Bayesian Model

Time-dependent Reproduction Number

1. Background

Severe acute respiratory syndrome coronavirus 2 SARS-CoV-2 has rapidly spread across the globe since December 2019 (1). Thus, the virus has demonstrated high infectiousness among susceptible populations. The first reports of human-to-human transmission of the disease were on 19th February 2020, and more than 146,600 laboratory-confirmed cases have been reported until 30th May in Iran due to community transmission (1).

The basic reproduction number (R0) is an epidemic threshold parameter that indicates the magnitude of infection transmissibility and may allow for prompt initiation of planning and implementation of public health and control measures. Mathematically, it represents the average number of secondary patients in a fully susceptible community at the beginning of an outbreak (2, 3). For demonstrating the persistence or dying-out of the epidemic, the quantity of R0 is compared with the unit value; these orders are R0 ≥ 1 or R0 < 1, respectively (3-5). During the first wave, the government of the Islamic Republic of Iran immediately began to impose restrictions on public gatherings and enhance the testing capacity. Thus, the number of infected people in the susceptible community reduced over time, and the effective reproduction number (Rt), which is defined as the actual average number of secondary cases per principal case when time > 0, could be computed. The R0 values for COVID-19 have been addressed in many countries, as well as Iran (2, 4-16). One study applied susceptible-infectious-removed (SIR) compartmental models to estimate R0 in the first 21 days of the epidemic in Iran (16). Another study used two methods, Generalized Growth model (GGM) and epidemic doubling time. The distribution of serial interval was as a gamma distribution (mean 4.41 ± 3.17 days), and the duration of the study was one month (7). However, the peak of the epidemic in Iran occurred in the first 40 days of the outbreak, which faded out later (1). On the other hand, several approaches have been proposed to estimate R0, such as exponential growth (EG) rate, Maximum Likelihood (ML), time-dependent (TD) reproduction number, attack rate (AR), sequential Bayesian (SB) model, gamma-distributed generation time, the final size of the epidemic, and Richard model (3, 17, 18). The use of these models is dependent on the type of data available. Hence, our aim in this study was to compare five approaches (EG, ML, SB, TD, and AR) to estimate R0 with the same generation time distribution and thus, determine the best fitting method.

2. Objectives

In our study, we intend to calculate the R0 of COVID-19 in the first wave of the epidemic (26th February to 30th March, 2020). We compared different approaches for estimating R0 in the early stage (26th February to 30th March, 2020) of the SARS-CoV-2 outbreak and discern the best fitting model.

3. Methods

The dataset was derived from cumulative laboratory-confirmed COVID-19 cases between 26th February 2020 and 30th May 2020 in Iran. The source of data can be found at https://www.worldometers.info/coronavirus/.

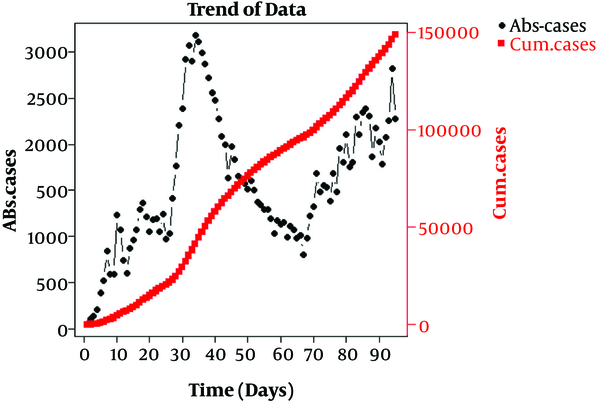
To estimate R0, the serial interval (SI) distribution was used as a proxy of generation time distribution (3, 11, 17, 18). The serial interval, i.e. time between symptoms onset in primary and secondary cases or time intervals between symptom onsets in primary cases and secondary cases (3). The distribution of SI was considered as gamma distribution (mean 4.41 ± 3.17 days) from a previous study (19, 20). Figure 1 shows that the first peak of the epidemic occurred at the end of the first 34 days.

Figure 1.

The incidence case count data between 26th February and 30th May 2020 in Iran

The equation of the EG method is

μ_{t} = (\sum_{i = 1}^{t} N_{t - 1} w_{i})

where

R = \frac{1}{M (- r)}

. In this equation “r” represents the growth rate of infection in the community, with Poisson regression; “M” is the moment generating function of GT; “N_t” demonstrates cases over a successive time unit, and “w” indicates GT (21).

The formula for the ML method is

L L (R) = \sum_{t = 1}^{T} \frac{\exp (- μ_{t)} μ_{t}^{N_{t}}}{N_{t}!}

where

μ_{t} = R \sum_{t = 1}^{t} N_{t - i} w_{i}

. Here, the sequential of N is denoted by N_t; “R” is the biggest value of the loglikelihood function (22), and generation time (w) is estimated by maximizing loglikelihood.

The TD formula is

R_{t} = \frac{1}{N_{t}} \sum_{t_{j = t}\}} R_{J}

where

R_{j} = \sum_{i} P_{i}

, and

p_{i j} = \frac{N_{i} w (t_{i} - t_{j})}{\sum_{i \neq k} N_{i} w (t_{i} - t_{k})}

. Besides p_ij in this equation represents the probability of sequential transition of infection between individual and. Also, R_j is the average of all transmission networks corresponding to the cases detected, and R_t indicates the mean of computed R_j (23).

Another approach to estimate R0 is the SB method with the Bayesian formula

p (R| N O, \dots, N_{t + 1}) \frac{p (N_{t + 1}| R, N_{O}, \dots, N_{t}) p (N O, \dots, N_{t})}{p (N O, \dots, N_{t + 1})}

. We presume that N_t+1 is the incidence case in time (t + 1) for an approximate SIR model with approximate Poisson distribution. The mean of this distribution is

N (t) e^{(y (R - 1))}

. Where

\frac{1}{γ}

indicates the average of the infection period. This Bayesian equation indicates a non-formative prior for R applied with this model, and the posterior R distribution in a previous time period has the same prior distribution for a later time period. For this model, the exponential distribution is used to express GT (3).

Lastly, the AR method equation to estimate R0 is

R 0 = \frac{\log (\frac{1 - A R}{S_{0}})}{A R - (1 - S_{0})}

. In this formula, AR and S₀denote the infection ratio and early susceptible ratio, respectively (24).

The values of R0 were simulated and sensitivity analysis was used to guide the selection of optimal time windows. The root mean square error (RMSE) was used to evaluate the models (3).

4. Results

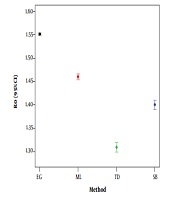
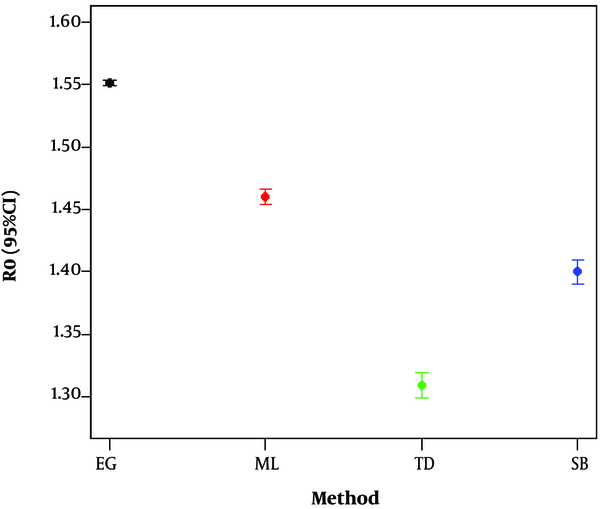
During the desired time period, we experienced one peak in the first epidemic time (26th February to 30th March, 2020) and after the fade-out, the second peak (from 10th May onwards) was probably ongoing (see Figure 1A). We obtained the estimated R0 [95% confidence interval] as follows: 1.55 [1.54; 1.55], 1.46 [1.45; 1.46], 1.31 [1.30; 1.32], and 1.40 [1.39; 1.41] using the EG, ML, TD, and SB methods, respectively.

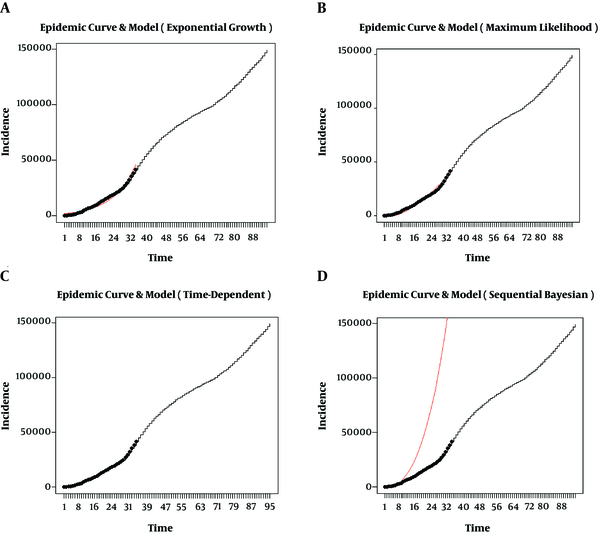
As seen, the range of estimations is various; however, the confidence intervals are narrow (Table 1 and Figure 2). The epidemic curves based on EG, ML, TD, and SB methods in Figure 3 represent the similarity of fitting curves and actual data, except for SB with poorly fitting time.

Table 1.Estimation of R0 by Five Approaches on the Same Dataset^a

Approach	Default R (%95 CI)	Optimal R (%95 CI)
EG
Optimal time window: 13 - 18	1.55 (1.54; 1.55)	1.68 (1.65; 1.71)
ML
Optimal time window: 14 - 34	1.46 (1.45; 1.46)	1.49 (1.48; 1.49)
TD
Optimal time window: 13 - 18	1.31 (1.30; 1.32)	1.43(1.41; 1.45)
SB
Optimal time window: 13 - 18	1.40 (1.39; 1.41)	1.50 (1.46; 1.53)
Optimal time window: 14 - 34		1.36 (1.34; 1.37)
AR
Optimal time window: 13 - 18	1.04 (1.04; 1.04)	1.04 (1.04; 1.04)

^aDefault times were obtained using data in the first 34 days. Optimal times are the best fitting time window. For the SB and AR methods, the optimal time window was obtained on day 18, as best fits the end of the exponential growth period, daily estimates were averaged over the 34 first days for the TD approach.

Figure 2.

Estimates of the reproduction ratio by four different methods

Figure 3.

Goodness-of-fit methods (observed incidence and predicted incidence for each method)

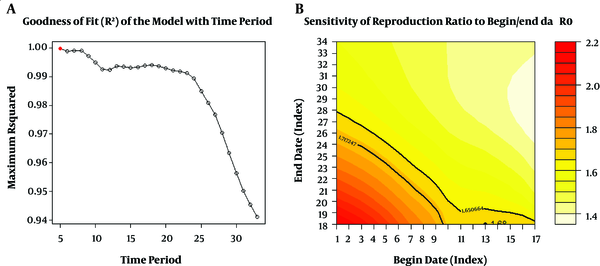
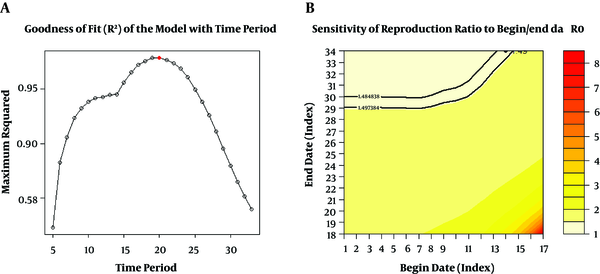
Sensitivity analyses were performed for both EG and ML methods to look for the best time window using EG. The largest R-squared (0.999) obtained was related to the period where the exponential growth model fitted the data best. The best fitting took place between time units 13 and 18 with a length of five days. Additionally, R-squared = 0.978 occurred between time units 14 and the epidemic peak point (34) with a length of 20 days. The goodness of fit is shown in heatmaps in Figures 4 and 5. The estimated R0s were 1.68 [1.65; 1.71] and 1.49 [1.48; 1.49] for EG and ML methods, respectively, as reported in Table 1.

Figure 4.

Sensitivity of the reproduction ratio to the choice of the time period by EG method. A, The red dot corresponds to the best value; B, The value corresponding to the best fit is shown as a dot, and the solid black lines show the limits of the corresponding 95% CI.

Figure 5.

Sensitivity of the reproduction ratio to the choice of the time period by ML method. A, The red dot corresponds to the best value; B, The value corresponding to the best fit is shown as a dot, and the solid black lines show the limits of the corresponding 95% CI.

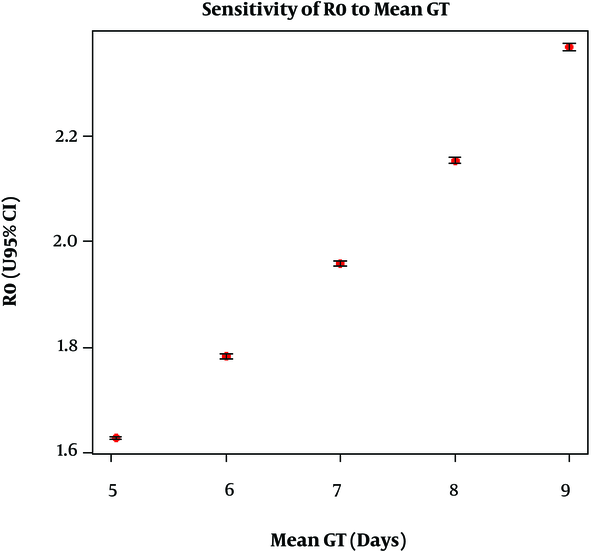
An important issue worth considering is how estimates change according to the choice of the generation time distribution (Figure 6). As expected, the estimates increased with the mean generation time. Thus, when the mean of GT varied between 5 and 9 days, R0 varied in the 1.628-2.369 interval.

Figure 6.

Sensitivity of the reproduction number to the choice of generation time distribution

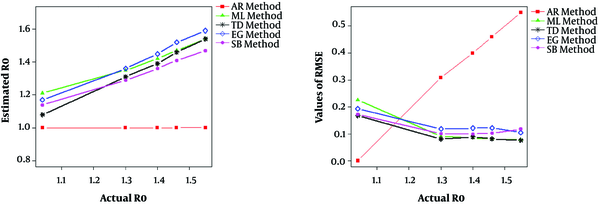
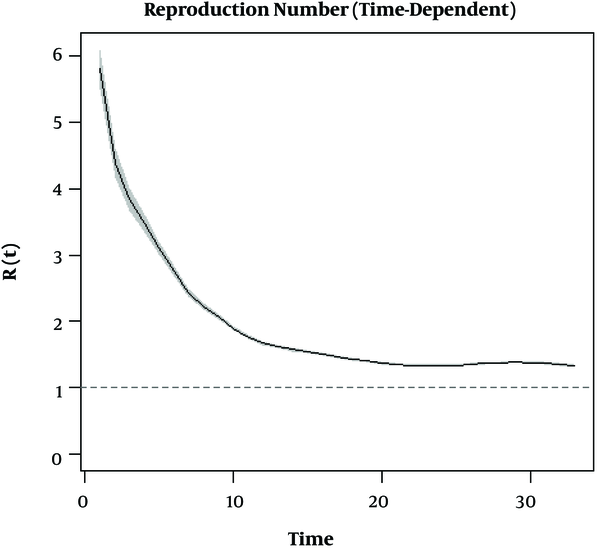
The results of 10,000 times of simulation and obtained RMSE and bias indices are shown in Tables 2 and 3. The TD method estimated the closest values to actual values among the other methods. In two observations, the TD and ML methods estimated values closest to the actual value, and in other observations, there were large differences. As a result, the TD method could be the best method with the optimal performance (lowest RMSE value) in estimating actual R0 values in this dataset (Table 3 and Figure 7). Figure 8 represents a descending trend of the reproduction numbers in real-time based on the TD method during the first peak of the outbreak. Moreover, the EG and ML methods displayed the overestimation of R0, and the SB method showed to be under-fitting in the estimate of R0. The AR method estimated R0 equal to one.

Table 2.R0 Estimation of COVID-19 Data Using Different Methods

Actual R0	Simulated R0 (95% CI)
Actual R0	EG	ML	TD	AR	SB
1.55	1.59 (1.50, 1.69)	1.544 (1.32, 1.79)	1.547 (1.16, 1.95)	1.00161 (1.00160, 1.00162)	1.47 (0.99, 1.91)
1.46	1.52 (1.43, 1.61)	1.47 (1.25, 1.73)	1.46 (1.03, 1.92)	1.00057 (1.00056, 1.00057)	1.41 (0.89, 1.89)
1.30	1.36 (1.27, 1.47)	1.35 (1.09, 1.65)	1.31 (0.73, 1.96)	1.000069 (1.000068, 1.000070)	1.29 (0.64, 1.90)
1.04	1.17 (1.07, 1.28)	1.21 (0.93, 1.55)	1.08 (0.28, 2.09)	1.000003 (1.000003, 1.000004)	1.14 (0.34, 1.91)
1.40	1.45 (1.36, 1.55)	1.42 (1.18, 1.70)	1.39 (0.91, 1.93)	1.000243 (1.000241, 1.000245)	1.36 (0.79, 1.90)

Table 3.Root Mean Squared Error and Bias Values of Reproduction Number Estimation for Each Method

Actual R0	RMSE (Bias)
Actual R0	EG	ML	TD	AR	SB
1.55	0.1094 (0.0460)	0.0777 (-0.0065)	0.0767 (-0.0040)	0.5495 (-0.5495)	0.1181 (-0.0807)
1.46	0.1224 (0.0608)	0.0820 (0.0184)	0.0816 (0.0179)	0.4596 (-0.4596)	0.1025 (-0.0485)
1.30	0.1186 (0.0574)	0.0918 (0.0487)	0.0812 (0.0168)	0.3090 (-0.3090)	0.1006 (-0.0119)
1.04	0.1937 (0.1784)	0.2258 (0.2188)	0.1679 (0.1306)	0.000757754 (-0.000757753)	0.1722 (0.1481)
1.40	0.1213 (0.0565)	0.0854 (0.0279)	0.0888 (-0.0076)	0.3997 (-0.3997)	0.1002 (-0.0354)

Figure 7.

Simulated R0 and RMSE values against actual R0 based on five methods

Figure 8.

Time-varying reproduction numbers during the outbreak of COVID-19 (26th February to 30th March, 2020); the shaded areas show the 95% confidence intervals

5. Discussion

Direct and indirect transmission besides short transmission time of SARS-CoV-2 has lead to the need for estimating the number of reproductions to assess the epidemic situation and take preventive measures. However, there are several methods that can be used to estimate the reproduction number, and thus the best-fitting model needs to be selected (3). In this study, five methods (EG, ML, TD, AR, and SB) were implemented, and the R0 estimations were 1.55, 1.46, 1.31, 1.04 1.40, respectively. In all cases, R0 was > 1. Our results suggested the TD method as the best method with the best performance for R0 estimation in this dataset.

The computed R0 based on the well-established method for Iranian cases of COVID-19 in the early stages of the epidemic was 1.31 [1.30; 1.32]. Thus, this infection persists. The World Health Organization (WHO) gave a preliminary R0 estimate of 1.4 to 2.5 (25). Liu et al. calculated the overall R0 to be 3.32 (2.81 - 3.82) for COVID-19 in a systematic review and meta-analysis (25). Muniz-Rodriguez et al. (7) applied the SIR method in Iran, and the range of R0 was estimated to be 4.86 in the first week to 2.1 in the fourth week of the outbreak (16). Another study used the GGM and doubling time methods and gamma distribution (7.5 ± 3.4 days) for SI. The R0 was computed as 4.4 [3.9; 4.9] and 3.50 [1.28; 8.14], respectively (7). Their estimated R0 values were larger than our estimates. However, it is important to acknowledge that differences in methods used and applying them to different epidemic distributions make it difficult for straightforward and direct comparisons to be made on numerical values between and within study results (3). To the best of our knowledge, our study is one of the first ones in the literature to compare common approaches on the same dataset and the same epidemic distribution for GT to estimate the R0 of COVID-19 in Iran.

The main aim of this investigation was to recognize the most well-established method for estimating R0; however, during this time, according to several recommendations by the Iranian Ministry of Health and Medical Education, the government closed educational centers, locked down activities, and used other confronting approaches from the earliest days of the outbreak on 24th, February 2020 (26). According to the advantages of TD as mentioned above, it seems that this method may have practical importance in evaluating time-dependent variations in the potential spread of COVID-19 to estimate R0 and Rt (27). Our results showed a decreasing trend of Rt from 5.80 (5.49; 6.10) on the first day of the epidemic to 1.30 [1.29; 1.31] a day before the first fade-out. Along the epidemic period, two factors resulted in time-dependent variation: intrinsic (reduction of susceptible individuals) and extrinsic (implementation of preventive measures). Thus, the estimation of R0 and Rt by utilizing the TD method can usefully monitor herd immunity and confronting approaches. In conclusion, the awareness of R as an epidemic threshold parameter for COVID-19 is useful to indicate the magnitude of infection transient and encourage the planning of control measures. Several mathematical models have been developed to estimate this parameter during epidemic courses. The best model is unknown. The TD method has several advantages, such as being the least biased, satisfactory correction for offspring cases due to the importation of cases during the outbreak, and no requirement for extensive and detailed data. Therefore, we propose this model to estimate R0 and Rt in Iran.

Footnotes

References

1.
WHO. Coronavirus. 2020, [cited 2020 May 30]. Available from: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports/.
2.
Farrington CP, Kanaan MN, Gay NJ. Estimation of the basic reproduction number for infectious diseases from age‐stratified serological survey data. J Royal Stat Soci. 2002;50(3):251-92. https://doi.org/10.1111/1467-9876.00233.
3.
Obadia T, Haneef R, Boelle PY. The R0 package: a toolbox to estimate reproduction numbers for epidemic outbreaks. BMC Med Inform Decis Mak. 2012;12:147. [PubMed ID: 23249562]. [PubMed Central ID: PMC3582628]. https://doi.org/10.1186/1472-6947-12-147.
4.
Khan A, Hassan M, Imran M. Estimating the basic reproduction number for single-strain dengue fever epidemics. Infect Dis Poverty. 2014;3:12. [PubMed ID: 24708869]. [PubMed Central ID: PMC4021574]. https://doi.org/10.1186/2049-9957-3-12.
5.
Safi MA, Garba SM. Global stability analysis of SEIR model with holling type II incidence function. Comput Math Methods Med. 2012;2012:826052. [PubMed ID: 23091562]. [PubMed Central ID: PMC3474276]. https://doi.org/10.1155/2012/826052.
6.
Khosravi A, Chaman R, Rohani-Rasaf M, Zare F, Mehravaran S, Emamian MH. The basic reproduction number and prediction of the epidemic size of the novel coronavirus (COVID-19) in Shahroud, Iran. Epidemiol Infect. 2020;148. e115. [PubMed ID: 32517845]. [PubMed Central ID: PMC7322167]. https://doi.org/10.1017/S0950268820001247.
7.
Muniz-Rodriguez K, Fung IC, Ferdosi SR, Ofori SK, Lee Y, Tariq A, et al. Transmission potential of COVID-19 in Iran. medRxiv. 2020. https://doi.org/10.1101/2020.03.08.20030643.
8.
Olfatifar M, Houri H, Shojaee S, Pourhoseingholi MA, Alali WQ, Busani L, et al. The Required Confronting Approaches Efficacy and Time to Control COVID-19 Outbreak in Iran. Arch Clin Infect Dis. 2020;15(COVID-19). https://doi.org/10.5812/archcid.102633.
9.
Read JM, Bridgen JR, Cummings DA, Ho A, Jewell CP. Novel coronavirus 2019-nCoV: early estimation of epidemiological parameters and epidemic predictions. MedRxiv. 2020. https://doi.org/10.1101/2020.01.23.20018549.
10.
Zhao S, Lin Q, Ran J, Musa SS, Yang G, Wang W, et al. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: A data-driven analysis in the early phase of the outbreak. Int J Infect Dis. 2020;92:214-7. [PubMed ID: 32007643]. [PubMed Central ID: PMC7110798]. https://doi.org/10.1016/j.ijid.2020.01.050.
11.
Viceconte G, Petrosillo N. COVID-19 R0: Magic number or conundrum? Infect Dis Rep. 2020;12(1):8516. [PubMed ID: 32201554]. [PubMed Central ID: PMC7073717]. https://doi.org/10.4081/idr.2020.8516.
12.
Zhang S, Diao M, Yu W, Pei L, Lin Z, Chen D. Estimation of the reproductive number of novel coronavirus (COVID-19) and the probable outbreak size on the Diamond Princess cruise ship: A data-driven analysis. Int J Infect Dis. 2020;93:201-4. [PubMed ID: 32097725]. [PubMed Central ID: PMC7110591]. https://doi.org/10.1016/j.ijid.2020.02.033.
13.
Velavan TP, Meyer CG. The COVID-19 epidemic. Trop Med Int Health. 2020;25(3):278-80. [PubMed ID: 32052514]. [PubMed Central ID: PMC7169770]. https://doi.org/10.1111/tmi.13383.
14.
Wang Y, Wang Y, Chen Y, Qin Q. Unique epidemiological and clinical features of the emerging 2019 novel coronavirus pneumonia (COVID-19) implicate special control measures. J Med Virol. 2020;92(6):568-76. [PubMed ID: 32134116]. [PubMed Central ID: PMC7228347]. https://doi.org/10.1002/jmv.25748.
15.
D'Arienzo M, Coniglio A. Assessment of the SARS-CoV-2 basic reproduction number, R 0, based on the early phase of COVID-19 outbreak in Italy. Biosaf Health. 2020;2(2):57-9. [PubMed ID: 32835209]. [PubMed Central ID: PMC7148916]. https://doi.org/10.1016/j.bsheal.2020.03.004.
16.
Sahafizadeh E, Sartoli S. Epidemic curve and reproduction number of COVID-19 in Iran. J Travel Med. 2020;27(5). [PubMed ID: 32419024]. [PubMed Central ID: PMC7542670]. https://doi.org/10.1093/jtm/taaa077.
17.
Nikbakht R, Baneshi MR, Bahrampour A, Hosseinnataj A. Comparison of methods to Estimate Basic Reproduction Number (R 0) of influenza, Using Canada 2009 and 2017-18 A (H1N1) Data. J Res Med Sci. 2019;24:67. [PubMed ID: 31523253]. [PubMed Central ID: PMC6670001]. https://doi.org/10.4103/jrms.JRMS_888_18.
18.
Nikbakht R, Baneshi MR, Bahrampour A. Estimation of the Basic Reproduction Number and Vaccination Coverage of Influenza in the United States (2017-18). J Res Health Sci. 2018;18(4). e00427. [PubMed ID: 30728313]. [PubMed Central ID: PMC6941634].
19.
Nishiura H, Linton NM, Akhmetzhanov AR. Serial interval of novel coronavirus (COVID-19) infections. Int J Infect Dis. 2020;93:284-6. [PubMed ID: 32145466]. [PubMed Central ID: PMC7128842]. https://doi.org/10.1016/j.ijid.2020.02.060.
20.
You C, Deng Y, Hu W, Sun J, Lin Q, Zhou F, et al. Estimation of the time-varying reproduction number of COVID-19 outbreak in China. Int J Hyg Environ Health. 2020;228:113555. [PubMed ID: 32460229]. [PubMed Central ID: PMC7211652]. https://doi.org/10.1016/j.ijheh.2020.113555.
21.
Chowell G, Diaz-Duenas P, Miller JC, Alcazar-Velazco A, Hyman JM, Fenimore PW, et al. Estimation of the reproduction number of dengue fever from spatial epidemic data. Math Biosci. 2007;208(2):571-89. [PubMed ID: 17303188]. https://doi.org/10.1016/j.mbs.2006.11.011.
22.
Chowell G, Nishiura H, Bettencourt LM. Comparative estimation of the reproduction number for pandemic influenza from daily case notification data. J R Soc Interface. 2007;4(12):155-66. [PubMed ID: 17254982]. [PubMed Central ID: PMC2358966]. https://doi.org/10.1098/rsif.2006.0161.
23.
Roberts MG, Nishiura H. Early estimation of the reproduction number in the presence of imported cases: pandemic influenza H1N1-2009 in New Zealand. PLoS One. 2011;6(5). e17835. [PubMed ID: 21637342]. [PubMed Central ID: PMC3102662]. https://doi.org/10.1371/journal.pone.0017835.
24.
Dietz K. The estimation of the basic reproduction number for infectious diseases. Stat Methods Med Res. 1993;2(1):23-41. [PubMed ID: 8261248]. https://doi.org/10.1177/096228029300200103.
25.
Liu Y, Gayle AA, Wilder-Smith A, Rocklov J. The reproductive number of COVID-19 is higher compared to SARS coronavirus. J Travel Med. 2020;27(2). [PubMed ID: 32052846]. [PubMed Central ID: PMC7074654]. https://doi.org/10.1093/jtm/taaa021.
26.
Esmaeilzadeh N, Shakeri M, Esmaeilzadeh M, Rahmanian V. ARIMA models forecasting the SARS-COV-2 in the Islamic Republic of Iran. Asian Pac J Trop Med. 2020 Nov 1;13(11):521. https://doi.org/10.4103/1995-7645.291407.
27.
Yamauchi T, Takeuchi S, Yamano Y, Kuroda Y, Nakadate T. Estimation of the effective reproduction number of influenza based on weekly reports in Miyazaki Prefecture. Sci Rep. 2019;9(1):2539. [PubMed ID: 30796315]. [PubMed Central ID: PMC6384943]. https://doi.org/10.1038/s41598-019-39057-w.

Import into EndNote Import into BibTex

Crossmark

Checking

Share on

Comments

Number of Comments:0

Cited by

Scopus by DOI: 0
Last Update: 3 weeks ago
Scopus by Title: 0
Last Update: 3 weeks ago
Scopus by Title (Ref): 0
Last Update: 3 weeks ago
CrossRef: 0
Last Update: 5 days ago

Metrics

Get Permission (article level)

Purchasing Reprints

Copyright Clearance Center (CCC) handles bulk orders for article reprints for Brieflands. To place an order for reprints, please click here ( https://www.copyright.com/landing/reprintsinquiryform/ ). Clicking this link will bring you to a CCC request form where you can provide the details of your order. Once complete, please click the ‘Submit Request’ button and CCC’s Reprints Services team will generate a quote for your review.

Search Relations

Author(s):

Nasrin Talkhi :[PubMed][Scholar]
Nayereh Esmaeilzadeh:[PubMed][Scholar]
Mohammad Taghi Shakeri:[PubMed][Scholar]
Zahra Pasdar :[PubMed][Scholar]

JAMM International

Outlines

Comparison of Different Approaches in Estimating Initial Reproduction Number of SARS-CoV-2 in the Islamic Republic of Iran

Abstract

Background:

Objectives:

Methods:

Results:

Conclusions:

1. Background

2. Objectives

3. Methods

4. Results

5. Discussion

Footnotes

References

Crossmark

Checking

Last Update: 3 weeks ago

Last Update: 3 weeks ago

Last Update: 3 weeks ago

Last Update: 5 days ago