1. Context
A lot of studies use standard statistical inferences, like hypothesis testing, confidence interval, and so on. The theory of these inferences is usually based on independent and identically distributed (IID) assumption (Neyman (1)). Moreover, common statistical softwares use the extended formula based on IID.
On the other hand, many studies are conducted on finite populations that are basically far from standard statistical assumptions (Sarndal et al. (2). Generally, finite population sampling designs do not generate IID samples except under some specified situations. So, it is very important to know if our sample is IID. One important and useful inference in standard statistics is Central Limit Theorem (CLT). CLT is based on IID, but for non-IID samples, the investigated theorem is far more complicated and different form standard cases (for more information see Chen and Rao (3); Fuller (4); and Hajek (5). Kozak (6) wrote a related note about the importance of distinguishing between finite and infinite populations. He looked at infinite population, as a case that generates IID sample.
2. Evidence Acquisition
Here, we are going to investigate some finite population cases to see whether they can generate IID samples. As an important point, we do not select between finite and infinite population, but we have to use one of them for our research, which is almost finite population case.
In section 2, we define and briefly explain IID sample. Section 3 contains the 3 famous sampling designs; simple random sampling (SRS), stratified sampling (StS), and cluster sampling (ClS). In this section we investigate the sample attributes and if it is possible to look at generated sample as an IID sample or not. The discussion will be ended by a conclusion in section 4.
2.1. Definition of Independent and Identically Distributed
In many situations for extending a statistical formula, there is a common sentence “Assume we have a random sample X1, X2, …, Xn of size n from a population (Fx(x)).” When we say random sample, it means a subset of independent and identical variables from the population. IID comes from “Independent and Identical.” In mathematics, we write: X1, X2, ⋯, Xn∶ iid f(µ, σ2), where E(X) = µ and Var(X) = σ2 are expectation and variance of X. To determine the IID of samples, first we should know the meaning of “Independent” and “Identical” terms.
2.1.1. Independence
X1, X2, …, Xn are mathematically independent if

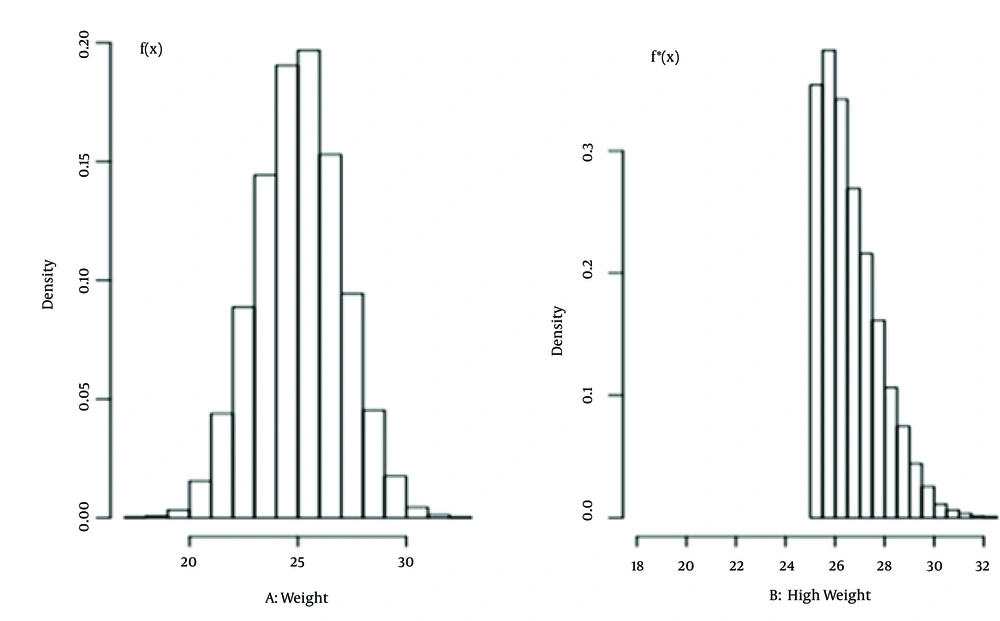
Conceptually, it means that information about one variable does not give information about the others. For example, assume that we are going to get a sample of size n from population of 11-year-old boys in Iran. In other words, X1, X2, …, Xn: iid f(25, 4) (Figure 1A).
Then, f is the density of respective variable, in the population. Function f indicates under what distribution the variable gets different values. For example in Figure 1A, we can see that P(Xi = 23.5) = 0.15. Now X1 and X2 are independent if observing X1 does not give information about X2. Mathematically, P(X2 = 23.5) = 0.15 and if we know X1 = 22, again P(X2 = 23.5|X1 = 22) = 0.15. Then, variables are conceptually independent, if observing one variable does not give information about others.
2.1.2. Identically Distributed
Mathematically, X1, X2, ..., Xn are identically distributed, if

and conceptually it means that all Xis come from the same distribution or all variables get different values under same probability or density function. In effect, in boy’s weight case, X1 and X2 are identically distributed if we select both of them from the same population or density function (f). For example, if we select X1 from f(x), it means from all population, and X2 from f*(x), it means from the boys with high weight (Figure 1B), then X1 and X2 are not identical. In Figure 1, in both A and B, one unit probability is distributed under the bars.
3. Results
3.1. Investigating Independence and Identically Distributed in Some Important Sampling Designs
Theoretically, it is easy to assume that a sample is IID but in practice, especially in finite populations, the situation is completely different. Now that we know the definition of IID, it is important to check some important sampling designs, to see if they generate IID samples.
3.1.1. Simple Random Sampling With Replacement
In this design, we select one of the population members, with equal chance of being selected, then the respective attribute of the member is recorded and the member is returned to the population and this procedure will be repeated until a sample of size n be recorded. Therefore, each member is selected in each stage of sampling with the probability of 1/N. Is this sample IID?
Assume we have a population of size N = 3 as: ⌊10, 20, 30⌋, and we are going to get a sample of size n = 2. Here f is:

Then, we take X1: f(x). Assume X1 = 20. Because this member is returned to the population, then X2: f(x) and they are identical. Also X1 gives no information about X2, and hence they are independent. Therefore, Simple Random Sampling with Replacement (SRSWR) generates IID sample.
3.1.2. Simple Random Sampling Without Replacement
In this design, the first sample unit is selected with equal chance for all population. The respective member will be excluded from the population and the second sample unit will be selected from the remaining population. In this design, it is easy to show that probability of selecting each member, in each specified stage is 1/N. Again assume our population is (1) and n = 2. Assume, X1 = 20, then P(X2 = 10) = 1/3 but P(X2 = 10|X1 = 20) = 1/2. Then, X1 and X2 are not independent. On the other hand, they are still identical, because they get different values with equal chance. Then, simple random sampling without replacement (SRSWOR) does not generate IID sample. As we know SRSWOR is more acceptable than SRSWR, because the former contains more information. What now? Can we use SRSWOR sample in standard statistical inferences?
3.1.2.1. SRSWOR When N Is Very Large Compared to n
Assume we have a large population of 1000 members with respective variable equals 10, 1000 equals 20 and the same for 30. ⌊10, 10, ..., 10, 20, 20, ..., 20, 30, 30, ..., 30⌋.
Now assume that n = 2 and X1 = 20, then P(X2 = 10) = 1000/3000 =1/3 and P(X2 = 10|X1 = 20) = 1000/2999 ≃ 1/3. Then, if N is very large in comparison with n (in practice n < 0.05 N), the design does not seriously violate independence. Thus, if N is very large, SRSWOR generates IID sample.
3.1.3. Stratified Sampling
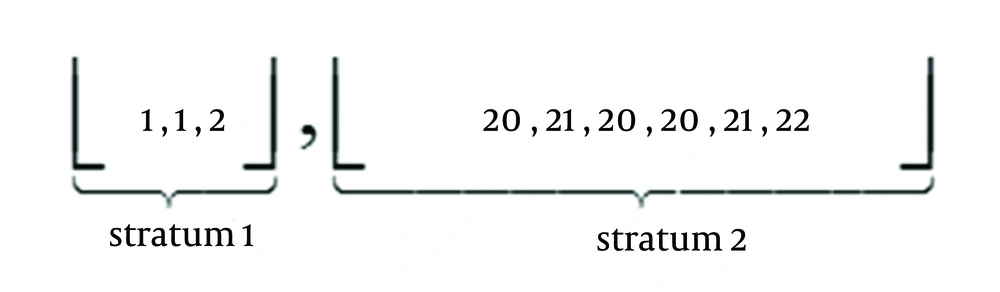
Statisticians seek two advantages in extending sampling designs: 1- improving precision 2- reducing costs. Stratified sampling was raised for the first purpose. In statistical surveys, it is advantageous to sample each subpopulation (stratum) independently, when subpopulations vary within an overall population. In such situation, according to the interest variable, the population is divided into homogeneous subgroups. The strata should be mutually exclusive. To get a sample, SRSWR or SRSWOR can be applied within each stratum. In addition, if inside each stratum is homogeneous and there are serious gaps between strata, StS is more efficient than SRSWOR. To improve precision, it is better to allocate bigger sample in stratum with more variation. Because it is difficult to have information about the variance of the strata, proportional allocation is a reasonable option. Assume we have a population, partitioned into H strata, each of size {Nh, h = 1, 2, ..., H} and we are going to get a sample of size n with proportional allocation. Then, a sample of size around nNh/N should be taken of hth stratum. Now, does this design generate IID sample? Assume we have a population partitioned into 2 strata as Figure 2.
And we are going to take a sample of size n = 3 of the population, then n1 = 1 (it is not reasonable to take a sample of size one but it is just an example) and n2 = 2. Now X1 will be selected from the first and X2, X3 will be selected from the second stratum. But

and

Then, Xis are not identical and therefore, StS design does not generate IID sample. Noticing that is very important because in many surveys to make inference about population, for example to test H0: µ = µ0, the sampler or designer for taking a “good” sample, plans to execute an StS design with SRSWOR. Then, the data will be put in an application like SPSS and the test could lead to misleading results, because the data are not IID, and standard inference for hypothesis testing uses formula based on IID assumption. For example, the test statistics will be

While the exact test statistic is:

Where,


and

Therefore, Z* = 0.38, Z = 5.7 and with wrong analysis (Equation 6), H0 will not be rejected, but with right analysis (Equation 7), H0 will be rejected strongly. However, according to previous sections, the sample of each stratum could be IID. Then it is OK if someone is going to do some analyses inside the stratum, or even compare strata for example by analysis of variance.
3.1.4. Cluster Sampling
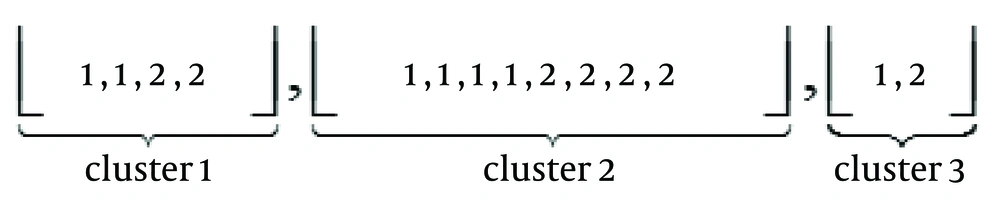
Cluster sampling was raised to reduce costs of sampling. If the population is partitioned into some subpopulations (strata) with variations inside each stratum, like all population, and there are no serious differences between strata, it is reasonable to choose few strata and get a sample inside them to reduce the costs of sampling. The population within a cluster should ideally be as heterogeneous as possible, but there should be homogeneity between clusters. Now does this design, generate IID sample? To answer this question, assume an ideal clustered population as Figure 3.
Then, we are going to get a sample of size n = 3 with proportional allocation of the population from two clusters. Assume clusters 1 and 2 are selected by SRSWOR and then we allocate X1 from cluster 1 and X2, X3 from cluster 2. Now,

Also, X2 ~ f(x), even if we take X from the whole population, again X ~ f(x) then the Xis are identical. Furthermore,

Then, each cluster represents the population, and if the size of the subpopulation is large enough, the Xis are independent, and therefore cluster sampling almost generates IID sample. A summary of the results are presented in Table 1. “Almost yes” means it can be satisfied under some lax conditions.
| Design | Independency | Identically Distributed | IID |
|---|---|---|---|
| SRSWR | Yes | Yes | Yes |
| SRSWOR | Almost yes | Yes | Almost yes |
| Stratified Sampling | Almost yes | No | No |
| Cluster Sampling | Almost yes | Almost yes | Almost yes |
3.1.4.1. Stratified for Spreading the Sample in the Whole Population
Researchers sometimes assume that the population is partitioned into some strata and take their sample with stratified sampling, but just to separate the sample in the whole population (for example because they think there might be a correlation between adjacent members). In such situations, maybe the strata are clusters, and then it can generate IID sample.
3.1.5. A Simulation
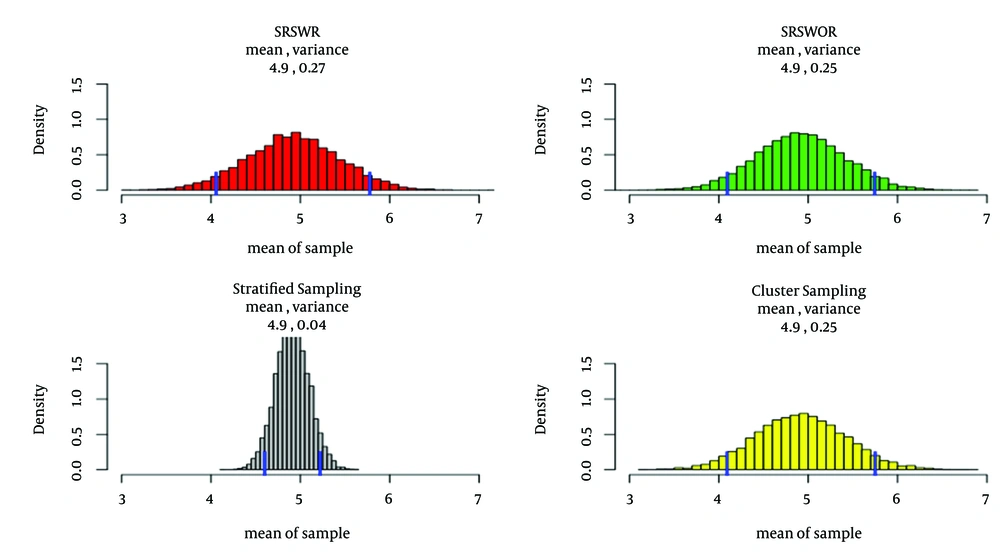
Here, we simulate a population of size 1000, with normal distribution, and the mean of the population of 4.9. We perform the 4 designs:
• SRSWR: a sample of size 100 of whole population,
• SRSWOR: a sample of size 100 of whole population,
• Stratified sampling: we decide to partition the population into 4 strata with the equal size of 250. To construct the strata, we first sort out the population, the first 250 forms the first stratum and the next 250 forms the second stratum and so on. Then, we take a sample of size 25 from each stratum.
• Cluster sampling: we decide to partition the population into 4 with equal size of 250. To construct the clusters we randomly partition the population into 4 clusters. For sampling, we randomly select 2 clusters of 4 and then we take a sample of size 50 from each of them.
As we can see in Figure 4, distribution of the estimators are the same for SRSWOR and cluster sampling (that use SRSWOR in the second stage sampling), distribution of the SRSWR is almost similar to the first two designs, but they are not completely similar because the size of sample is almost significant. For stratified sampling, the situation is completely different. As we expect, this strategy could be much more efficient than the others. Also, 95% confidence intervals are almost the same for the first 3 designs and more precise for stratified sampling.
Mean and variance of the estimators, computed using Monte Carlo method, with 10000 iterations, are presented. The blue lines indicate 95% confidence interval. The results are almost the same for SRSWR, SRSWOR, and cluster sampling that almost generate IID samples. Stratified sampling shows better estimation compared to others because of its smaller error and its sample is far from IID assumption.
Thus, as discussed before, cluster sampling and SRSWOR almost generate IID sample like SRSWR and for stratified sampling the situation is completely different.
4. Conclusions
Planning a design to sample a population is one of the important stages of a research. The next stages (analyzing the data and making conclusion about population or process) strongly depend on the first stage. Common statistical inferences are based on IID samples. IID samples are not produced in practice, especially in finite population cases. However, it is not bad news if our sample is not IID. For example, in many extended sampling designs for estimating mean of a population, the sample is not IID, but the design can estimate the unknown parameter with very small error that is not almost possible with an IID sample. Just researchers should be aware not to use this sample in statistical inferences such as standard hypothesis testing and confidence interval. To make such inferences, the formulas should be adapted for the design.
In this article, we explained that even in finite population cases, with some designs and under some conditions, IID sample can be generated and there is no worry about using standard statistical inferences.