1. Introduction
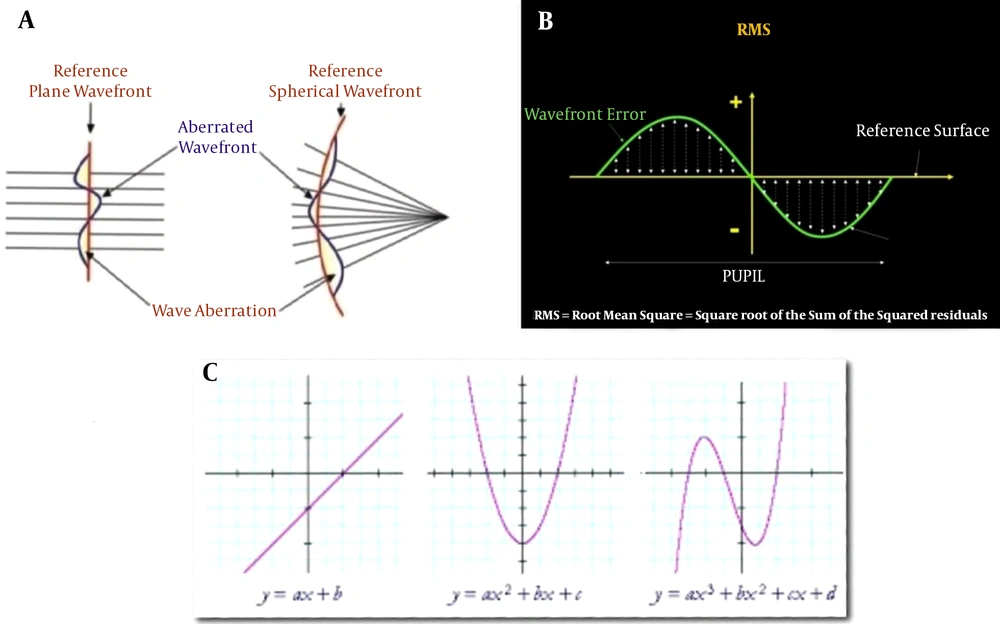
Different methods are used for aberrometry which are divided into two groups: (1) outgoing, and (2) incoming. In the incoming aberrometry method, such as ray tracing or Tscherning , the infrared light is trace on the retina it is then compared with a photodetector pointing point on the retina with a pointing point on the retina reference compared that has no aberration (1-3). In the outgoing method, such as the Hartman shack, the infrared beam of laser light travels over the retina the reflex light that will be parallel to normally passes through the lenseset and then focuses on a sensor called a charged coupled device, the surface of the sensor contains several rows of squares, the center of each of which will be the focal point of the optical lens (4). If there are aberration on the wavefront that is out of eye their light focus will shift from the center of these squares and the sensor will sense and measure them and will show the deviation of each point on the wavefront quantitatively in microns and qualitatively with the map. the value of the deviation of the wavefront from the reference surface is shown in micrometers. When it is positive, the wave front is ahead of the reference level (such as myopia) and when the wavefront is behind the reference level (back), it has a negative sign (such as hyperopia). Because the wavefront values are quite variable compared to the reference level, they give different values for each wavefront (5, 6). The device reports the sum of statistics and because the numbers obtained may also be negative, the second power of them is added together, and then the second root of this sum (root mean sqare or rms) is reported as the determinant of the aberration (Figure 1B). It also device shows the aberrometry qualitatively with a map the green areas correspond to areas of the reference surface in the pupil range that do not deviate from the wavefront (the deviation from the wavefront is in the zero micron range) and the yellow and red zones are the zones of positive deviation and the blue and purple zones are the zones of negative deviation (Figure 1C).
Now a clinician or refractive surgeon should be able to interpret and analyze the data obtained from the aberrometry to provide a therapeutic solution. For example, correcting them by prescribing glasses, or by prescribing lenses, or correcting by excimer laser or other methods. But since the results of the aberrometry have a complex and mixed form of aberration that is unclear to the physician, measurement aberrometry has to be broken down into basic components that usually have a simpler form and that the physician can make it easier to interpret and find a cure.
These basic components were expressed mathematically many years ago by Fritz Zernike (a Dutch physicist and nobel laureate for the invention of contrast-phase microscopy) which became known as the Zernike modes, which are arranged in a special pyramidal order (7).
Zernike modes or pyramids are fundamental forms that show different distortions using polynomial equations. These equations usually have one variable which on the function of coefficient and power is applied and the result is a polynomial equation that shows a particular shape when plotting it in a two-dimensional coordinate system for example, if the variable power is one, the drawing shape will be a line, and if power is two, the parabola and if the power of three is similar to the letter N and so on (Figures 1C and 2A).
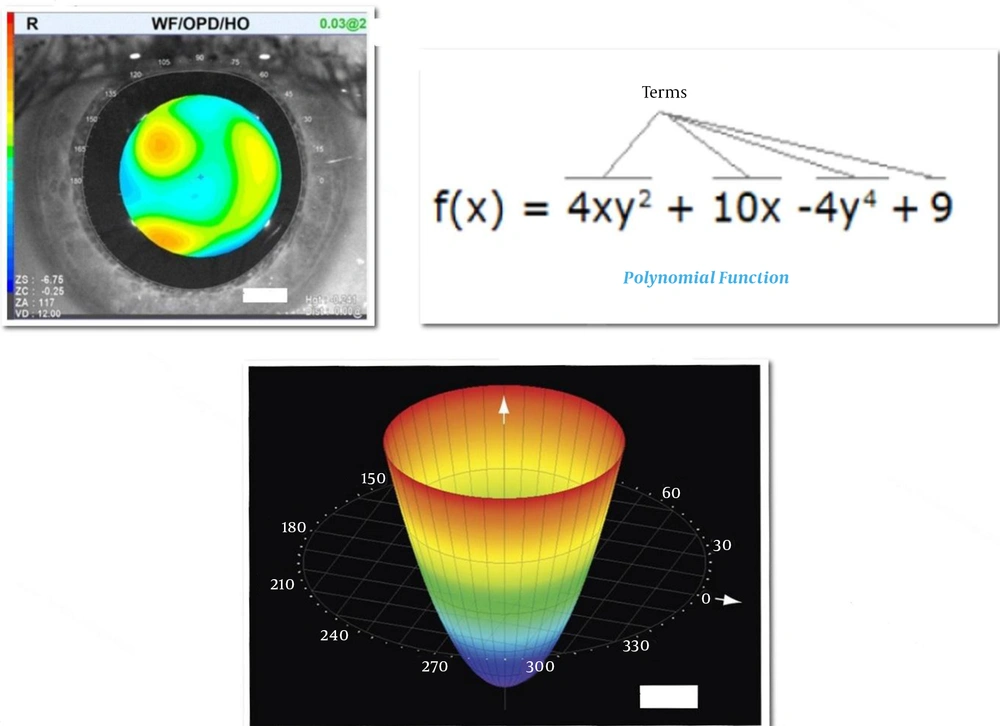
Optically, the variable x is, in fact the distance from the center of the pupil and is represented by r in millimeters.
Thus, for example, if the equation with r is represented by the power of two, the level of distortion will be one parabola relative to the reference level, as shown in the following three-dimensional view (Figure 2B). Which in Zernike modes, known as defocus, as the power and number of sentences increases, the equation becomes more complex, for example the power equation of three which will be in the form of Figure 2C.
Figure 2C is in the form of Zernike known as coma (8, 9).
The highest power in a Zernike polynomial equation represented by the symbol n, which is an integer. The number of sentences and their power indicates the curvature that the surface of the wavefront finds relative to the reference surface, which is in fact the pupil entrance. These two levels are parallel to each other but can be considered to be not parallel to each other, that's mean they are tilted horizontally or vertically in this case, the complexity of the Zernike forms is added (10, 11). The wavefront surface is tilted relative to the reference surface is represented by an integer m, the θ is the angle between these two levels. When m is positive the tilt is horizontal, then cos θ angle that determines the equation and the shape of the distortion, and if the tilt is vertical, m will be negative and sin θ will determines the equation and the shape of distortion.
Thus two numbers n and m represent a particular mode, n known as radial frequency and represents the highest power in the transaction and changes vertically in the Zernike pyramid and m is known as the angular frequency, and indicates the tilt of the wavefront relative to the reference surface and changes horizontally (m is always less or equal to n). n and m are either even or odd, so that the half of these difference two numbers is equal to an integer.
Therefore, in general, each Zernike mode is represented by the Zmn symbol. Thus very simply any Zernike mode is a mathematical equation that represents the coordinates of each point of the wavefront relative to the reference surface with two variables r to mm and angle θ to degrees (12).
If r is the distance of a point with a certain distance from the center of the pupil (the reference surface) and t is the angle between the reference surface and the wavefront and z is the corresponding point on the wavefront:
2. Evidence Acquisition
2.1. Equation 1
But expressing different modes with this simple equation has the drawback that it is not possible to make quantitative comparisons between different shapes, also these different forms cannot be added or subtracted, because as mentioned, this equation must be mathematically capable of decomposing the general mode of aberrometry into fundamental modes (13-15). For this reason, the above equation has to be mathematically normalized so that it can be done in two ways:
- Normalized relative to the radius of the pupil: In this case, the radius of the pupil is considered to be between zero and 1 (normalization to unite radius) as a result, it is possible to compare the same modes but with different pupil radius.
- Normalization to different quantities (normalization to unite variance) which it makes it possible for different modes to be comparatively and quantitatively comparable with each other, and at the same time to be able to add or subtract from each other, which is why the Zernike modes are called orthogonal and orthonormal.
The mathematical operation to normalize leads to the general formula in Figure 3.
2.2. Equation 2
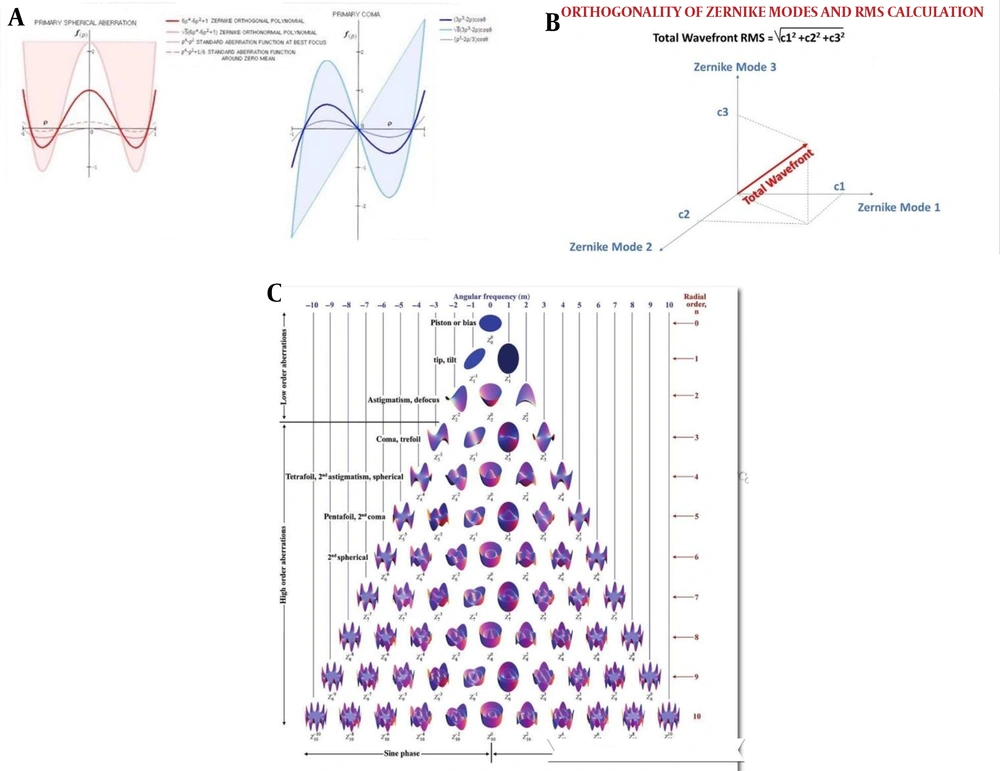
In the above equation K is an integer between zero and half the sum or half of the subtraction of two numbers m and n, and t is the angle between the reference surface and the wavefront , thus by putting them in this formula the equation for each of the Zernike modes items is determined. It is noteworthy that the positions of these modes are considered relative to the (zmc) zero mean circle in this way, the reference level of the pupil is considered zero, as a result the wavefront deviation from the reference surface is evenly distributed between the two sides of the reference surface. This is well illustrated in Figure 4A that in zmc the amount of positive and negative deviation is equal and the sum of deviations is zero.
There is an exception, that is spherical aberration which on both sides of zero mean is not equal and the deviation on one side is 1.5 times the other. it is also shown in Figures 2B and C that the points on the green area are at the periphery of the pupil, that's mean they have a deviation of zero, and the dots on the blue and purple areas are behind the pupil and are therefore negative, and the yellow and red areas are in front of the pupil and are therefore positive (16, 17).
Expressing deviation from zmc is actually part of the normalization process, and therefore does not mean that in any aberration the wavefront shape is relative to the reference surface, for example if it was in defocus (Figure 2B) to be placed a apex of parabola on one side of the reference surface and the ends of it on the other side then must be in defocus aberration; in the center of the pupil hyperopia and in the peripheral part of the myopia, which, of course is not the case.
In addition to expressing the mean deviation relative to the zero mean, expression of deviation relative to the reference level is also done also called the standard deviation at best focus. In this case the total deviation is considered on one side of the reference surface, so it will be generally positive or negative. In fact, the actual shape of the wavefront aberration relative to the reference surface in different shapes is the same shape.
Figure 4A is a Spherical abrasion and coma are given in which various deviations from the reference level are shown. as shown in these figures in standard form the best focus is deviation on one side of the reference level, which is actually the case but the deviation around the zero mean square is on both sides of the reference surface, when comparing the deviation range on both sides of the spherical aberration reference surface with coma we find that in coma these two levels are equal but in the spherical aberration the ratio is 3: 2.
Also note that measures of deviation they are much smaller in standard dimensions than orthogonality and orthonormality. Because the dimensions of these two terms were for normalization, they have increased so that they are in fact perpendicular to the Zernike modes, which is orthogonality, this means that the quantity of each one is completely independent of the other modes and has no effect on the quantity of the other modes. In addition, different modes can coalesce and result in new modes, such as the defocus mode (Z02), which is completely independent of the spherical aberration mode (Z04) but can be assembled with it (18, 19).
As can be seen in Figure 4B, modes 1, 2, and 3 are perpendicular to one another and can be aggregated and the sum of their results considered as a new mode.
Thus, according to equation 2, each case of modes Zernike can be determined and plotted, and each mode is represented by Zmn, each with modes n vertically increasing and m increasing horizontally in Zernike's pyramid.
The vertex of the pyramid is Z00, that amount of deviation is constant in all parts of the reference surface and the total deviation is displayed in one color (the Zernike coefficient is equal in all parts) this mode is known as piston.
The second row is Z11, Z-11; which corresponds to horizontal and vertical tilts. In this type of deviation, r is one power, thus the deviation at the surface of the pupil changes linearly, so the deviation of the wavefront relative to the reference surface is only tilted and the curve is not.
The third row is in the middle of Z02, which is a part of the defocus, r is the power of two (the curve has a turning point) without any tilts since m is zero. If the parabola is ahead of the reference level, it will be diffuse myopia and if it is behind the reference level, it will be hyperopic.
The right side of the Z22 is with or against astigmatism, and the left side of the Z-22 is the oblique astigmatism. These two modes are in fact the same as the defocus that is tilted horizontally or vertically.
The first three rows of deviation modes are known as low order aberration because they are structured in such a way that they can be modified with glasses.
The fourth row on is high order aberration which cannot be corrected by glasses.
The fourth row consists of Z13 and Z-13, which are horizontal and vertical coma respectively in these two modes, the r mode has a power of three (the curve has two turning points) and is tilted horizontally or vertically.
Fourth row side modes are Z33 and Z-33, which are known as shamrock or trefoil aberration. These modes are actually the result of horizontal or vertical horizontal tilting and vertical tilting.
The fifth row, located in the middle of Z04, it is spherical aberration, in this mode r is to the power of four and and it has no tilt. This mode is in fact a higher-order of defocus but resembles a cylinder rather than a parabola and because of having the statement «r» at power two in equation, there is also a tab in the center (it has three turning points).
The difference between defocus and spherical aberration with respect to their curve shape is clearly evident, in defocus the deviation from the center to the peripher gradually increases, whereas in spherical aberration from center to peripheral there is no deviation, but abrupt deviation occurs in the peripher.
On both sides of the spherical aberration are the Z24 and Z-24, which are known as second order astigmatism. In fact, these are the same stigmatisms that have the power of four. When these two modes are tilted horizontally or vertically, they create side modes which are Z44 and Z-44 respectively and also known as tetrafoil.
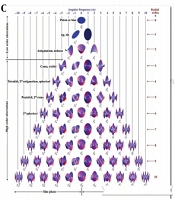
In the same way, with increasing n and m, the rows of the Zernike pyramid increase, and the higher the row, the number of modes in that row increases (Figure 4C).
In the Zernike pyramid, each mode is 2n away from its similar mode for example Z22 astigmatism is in the first order (r power two) and Z24 astigmatism is second order (r power four) and the latter, also the Z13 is first order horizontal coma (r is power of three) and the Z15 is a second-order horizontal coma (r of power five) and so on.
The side of the pyramid is the trefoil from the third row onwards that fourth row is Terfoil Z33, fifth Tetrafoil Z44, sixth Pentafoil Z55, seventh Hexafoil Z66 and so on. In the Figure 4C, the Zernike pyramid is brought down to order ten (n equal to ten) but in fact it can continue to infinity, but because with increasing order aberration, their prevalence decreases. In ophthalmology order higher than six does not matter and is not considered, however in the construction of other optical systems such as microscopes and telescopes higher orders may still be important and considering them can affect their image quality (20, 21).
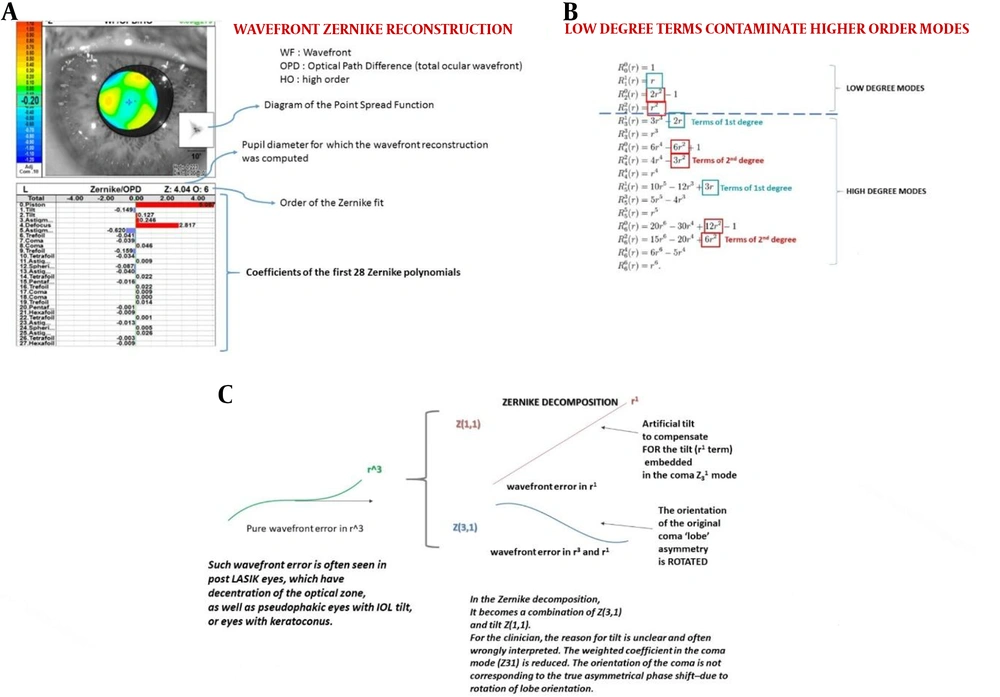
As mentioned, each of the modes of Zernike is attributed to a mathematical expression, which is a polynomial equation whose variable is r which is the distance from the center of the pupil. Another variable is the angle θ, which is the angle between the wavefront and the reference surface these expressions are called polynomial orthonormals (equation 2). by placing the value of r and the size t, a number is obtained which is called the "Zernike cofficent" at a certain distance from the center of the pupil (for example, the Zernike coefficient at a distance of one millimeter from the center of the pupil about the spherical abrasion (Z04) according to its equation equals radical five).
Of course, scientifically, the term "Zernike coefficient" is not correct and the more accurate term is Zernike aberration term, but most of the texts refer, in this article this number is also called the Zernike coefficient (Figures 5A and B).
Now the question is, that according to what was said, how do the abirrometers which are obtained in different ways, become the types of Zernike modes described above? As illustrated in the figure, Zernike modes that have the ability to come together to form a particular mode with a certain quantity. What is measured in abirrometry is actually a result of the sum of several modes of Zernike that by knowing the coefficients of each of these modes, we can determine how many aberrometry performed, includes how many Zernike modes and what is the weight (what percentage) of the measured abirrometry.
The value of the coefficient is determined by knowing r and delta, for example, for Z02 or defocus mode, if the value of r is zero, it will have a coefficient equal to radical minus three also for r = 1, its coefficient will be a positive radical of three. In this way, the Zernike ratio is obtained for different modes any point. by determining these coefficients as well as measuring the amount of deviation at several points (at least in the number of modes that we want to decompose the general aberrometry into them) several equations simultaneous can be used by solving them, it is possible to determine the weight percentage of each of the Zernike modes and decompose the abirrometry to the zarnike modes.and for example, determined that a patient's abirrometry having rms equal to Z microns, how much of the piston (Zp), how much of the diffuser (Zd), how much of the coma (Zc), and what amount of other modes and abirrometry maps can also be decomposed into Zernike modes (Figure 5C).
In the same way, having information about 28 points, abirrometry can be broken down into 28 modes related to the first 6 order of the Zernike pyramid. Most abirrometers have computer programs that can perform mathematical calculations and break down the obtained abirrometers into Zernike modes. The device may then perform the results as in Figure 6A.
Figure 6A is the aberrometry patient with the Nidek company OPDscan, which breaks down the performed aberrometry into 28 Zernike modes and determines the weight of each ,the red color is the deviation ahead of the reference level which is positive, and the blue color is the deviation behind the reference level which is negative, as shown in the image the machine is based on the type of Zernike aberration that it has analyzed [point spread function (PSF)] which actually reflects the quality of vision has also simulated. PSF displays a simulated image of a spot on the retina which is distorted due to aberration and may be seen in other forms instead of one point (of course, even if there is no aberration, the optical system is perfectly ideal (best focused) again the image of a point will not be a point, but a circle created by the phenomenon of light scattering from the edges of the pupil or any other aperture (which is called the airy disk).
Now the question arises, how much valid is this analysis? How consistent it is with clinical reality? For example, in the example above, aberrometry is related to a disease with a deviation of rms of about 9 microns, is it really if 9 microns, to decompose into Zernike modes 5 microns related to the piston and 2.8 microns to the defocus and 0.6 microns to the oma?
Zernike's Basic modes more than clinical logic has mathematical logic, mathematical logic can be used to a great extent in the construction of optical devices but it can really be just as useful in understanding the optical system clinically in ophthalmology? This is important clinically and therapeutically when a physician experiences coma or spherical aberration and must know the exact amount to treat it with laser or other methods. If their assessment is incorrect, their treatment protocol will probably not be correct, and the patient's treatment outcome will not be the desired outcome.
as mentioned, to normalize and orthogonalize the initial equations describing wavefront aberrations, changes are made to them using mathematical principles, do these changes bring them closer or farther to clinical reality?
Dr. Daniel Gatinel believes that the being orthogonal, equations and modes of the Zernike however, it has made it possible to put them together and as a result aberrometry obtained from the devices can be analyzed, but at the same time it has caused some high order modes to have low order values or, as Gattinel claims, high order modes with low order modes to contaminate because there are some low order sentences in the high order equations (Figure 6B).
In the example in Figure 6B, Dr. Gattinel has shown that there are some low order sentences that should not exist in high order but they are necessary to maintain orthogonality, so high order modes are not completely pure and have a low order effect in themselves. for example, as mentioned above, the spherical aberration equation (Z44) that r is the power of four, has a sentence of two powers because of this spherical aberration, which should be the shape of a cylinder, it also has a portion in its center that shows itself as a tongue at the base of this cylinder (Figures 4A and 7B) as a result, the use of Zernike modes for aberrometric analysis may confuse clinician.
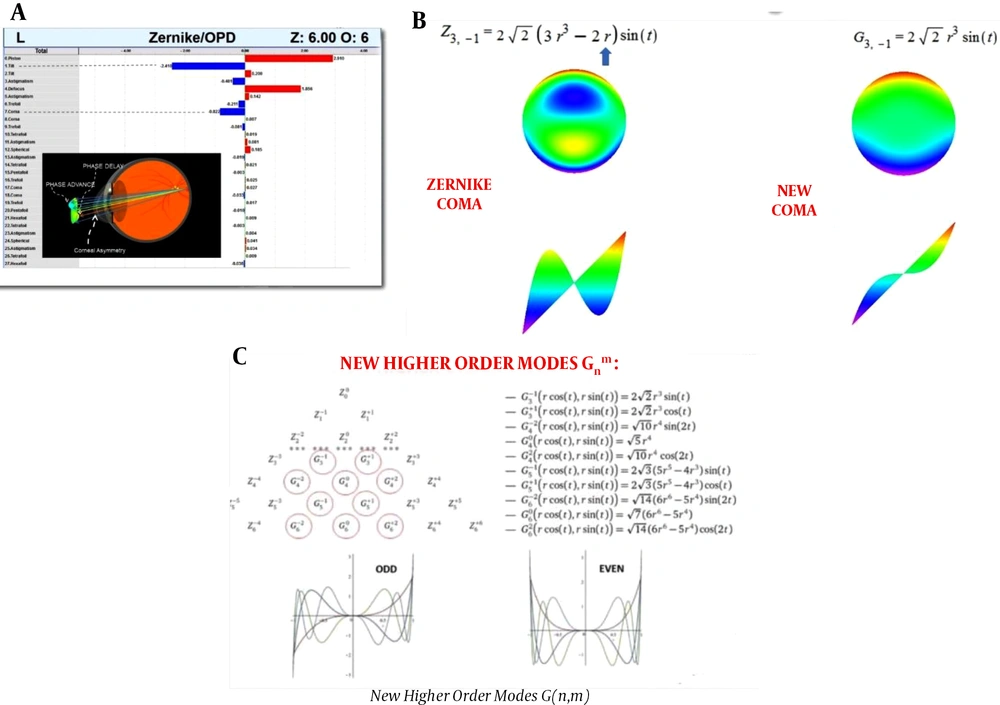
Another example is coma (Z13) that basic mathematical expression is «r» at power 3 also has the expression «r» at power 1 which corresponds to the tilt mode (Z11) as a result, first the Zernike coma mode (or more accurately artifact) it has tilt, and secondly because of the negative expression r, as a result, the device shows a coma to a lesser extent (understimate) as in Figure 6C.
For example, Figure 8A shows an aberrometric decomposition of a keratoconus case by an OPD scan device. We expect to have a major share of coma aberrometric decomposition in the keratoconus patient but as expected, the coma share is less than expected, instead the share of negative tilt (vertical tilt or Z-11) is high. for the reasons stated, this tilt is an artifact due to the addition of the sentence r to the power of one to the coma mode.in addition the same sentence reduced the amount of coma that we expected to be higher in keratoconus.
For this reason, Gattinel proposes that in the Zernike coma, the negative expression r to the power of -1 is deleted, and instead of the Z1-3, which represents the vertical coma of Zernike, it offers the G1-3 (Figure 8B).
In the case of other high order modes located in the central part of the Zernike pyramid, a similar proposition is generally given for modes 3 and 5 with the power of one and in the modes of 4 and 6 the power of two is omitted from the Zernike equation. Of course, because the side modes of the Zernike pyramid do not have the problem of low order contamination, they do not need to change. Figure 8C shows the modified modes using G instead of Z and a circle is drawn around it.
In this way, the first order and second order of the Zernike modes related to spherical aberration and coma, and the second order and third order modes of astigmatism are changed.
Of course, the fact is that it is difficult to show clinically which of the modes Zernike or Gatinel are more accurate. Because it is about understanding the quality of the patient's own vision and it cannot be shown objectively. Of course, there are indirect ways that clinician can use to evaluate the accuracy of aberrometric analysis for example, Zernike based aberrometric analysis will show how much aberration is low-order and so it is correctable with glasses, if according to what has been said, this analysis is not correct for any reason, therefore the amount of vision correction with glasses may be less or more than what the device has analyzed as low order.
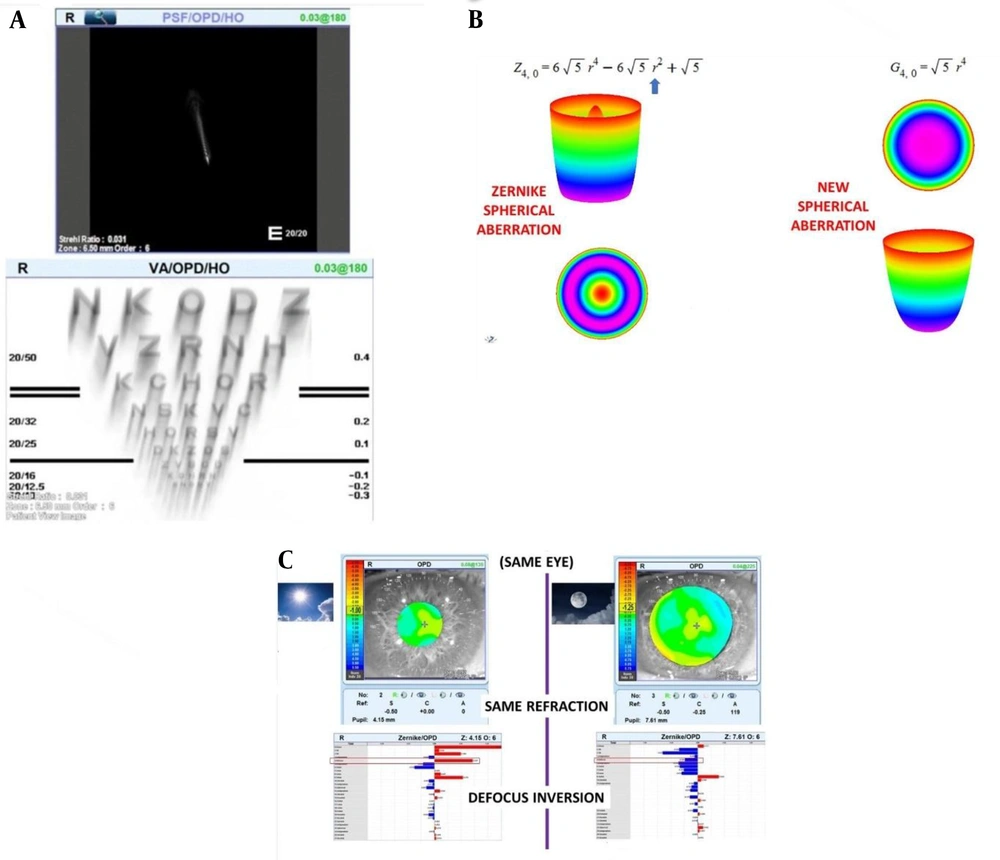
Another way is to compare what the patient perceives from the PSF or what he or she sees from the letters E chart or other letters with what the device simulates and see how it fits.
Figure 7A the device simulates the PSF of patient. here we can ask the patient to draw what he or she sees from a point image and then we see if this point that the patient has drawn is similar to the PSF of the device, which is simulated based on the analysis of aberrometric values is it or not. (Figure 7 PSF device simulates a coma patient's resembling a comet).
Also in Figure 7A, the device also predicts visual acuity using a snellen chart and and she simulates it in a way that the patient probably sees. So we can try it too or ask of patient to draw the letters that they see from the visual acuity chart, then compare what the patient sees with the simulated device if very similar, it may indicate the accuracy of the analysis of the device on the basis of Zernike modes or other modes.
Another way is to interpret the maps of each mode based on best focus. As mentioned, the best focus is the actual expression of the wavefront deviation from the reference level and its description must match the type of aberration. For example, defocus aberration (Z02), whose shape is parabola consider, in best focus mode the vertex of the parabola it is exactly at the center of the pupil tangent to the reference surface. as a result, there is no deviation in the center but toward the peripher gradually and with a steep gradient the distance between the existing wavefront and the reference level there is a gap that corresponds to hyperopia and myopia (if the defocus curve is ahead of the reference level, it will be myopia and if it is behind, it will be hyperopia) as a result, at the center section patient with defocus, he will have good vision (provided the pupil is tight and pint point mode) but with the pupil opening to the normal level (ie, not a pint point) the patient's vision declines.This also applies to spherical aberration mode (Z04), as shown in Figure 4A.
In best focus mode in the center of the wavefront such as defocus, it is tangent to the reference level. therefore, it does not have a deviation in the center, but like defocus it gradually moves away from the reference level towards the environment and reaches a maximum in mid peripheral and in the more peripheral part, the distance is reduced again to zero in the preipher, but in far periphery again and this time with a much steeper slope, it moves away from the reference level as a result, if the spherical deviation is considered in front of the reference level, the patient has good vision in the center (provided that pupil not too dilate).
At mid peripheral is myopic (pupil mid dilate) and in far preipheral the myopia intensity is much higher because on the spherical edges of aberration the slope of increasing distance from the reference surface is much greater than defocus. Thus we expect the person with spherical aberration according to Zernike mode, in middilate pupil mode have a vision disorder in form of hallo and in severe dilatation this disorder becomes much more severe.
In Figure 7B, the spherical modes of the Zernike aberration (Z04) are compared with the spherical aberration of the Gaitinel (G04). mode Z04 in terms of formula r is the power of 4 and so it has a cylindrical shape (in principle, in polynomial equations the pair power equals the state parabola and the higher the pair's power, the more it looks like a cylinder and looks like a square at high power) but because it also has the factor r of power 2, there is a parabolic shape at the center of the cylinder(defocus) so it has tabs in the middle of the cylinder it is the same tabs that, according to what was said above, does not cause deviation in the central part but in the mid peripheral part (again because of the factor r to the power of two) there should be deviation and in far peripheral because of the factor r power 4, deviate with a steeper slope and so from mid preferal onwards, that is with the average pupil, the person suffers from visual impairment and hallucinations.
But in the mode that Gattinel suggests (G04) by removing r to power 2 the shape of the deviation, which is the same cylinder, no longer has this tab (parabola or defocus) and the shape of the deviation of the wavefront from the reference surface will be quite similar to a pure cylinder. Here, also in best focus mode, such as defocus in the center tangent to the reference surface and not have deviation but by moving away from the center it has a cylindrical deviation not a parabola. So like the defocus deviation (parabola) it does not deviate rapidly from the reference level and in middle pupil range it will have good vision but in peripheral segment the abrupt, steeply sloping part of the peripheral, it is far from the surface and deviates. Thus, unlike Z04 a person with G04 mode with low to moderate dilatation does not experience halo but when the pupil opens more than mid peripheral, it suddenly and with more intensity becomes a halo.
In summary, this is the clinical difference between Zernike and Gatinel that person with spherical aberration with Zernike mode with a tighter pupil than with spherical aberration with Gatineal mode has a problem with halo.
Of course Dr. Gatinel to refute the spherical aberration of Zernike using Figure 7C, he gives some reasons which, in the author's view, is not true and is illustrated in Figure 1A.
Overall, according to the interpretation of the two spherical aberrations of Zarnike and Gatinel, tests can be designed to compare these modes to find out which one is more correct. In any case, if Dr. Gattinell's proposed modes are more consistent with clinical facts there is a big problem with these modes and it is loss of their orthogonality. Therefore, mathematically, the decomposition of the aberrometric map into Gattinell modes is a serious problem and a solution must be found for it.
3. Conclusions
There are no strong clinical reasons for Zernike modes to be a fully accurate description of aberrometry, so clinicians should consider other clinical data and findings in their interpretation.
In the aberrometric analysis shown in this Figure 7C, Gattinel explains the weakness of spherical aberration because according to this aberration there is myopia in the central part and hyperopia in the peripheral part. As a result, in the photopic pupil (day) the patient is myopic and in the mesopic pupil (dim light) the patient becomes hyperopic. While it is clear that there is no such case of aberration clinically. Gattinel concludes on the basis of this argument that Zernike spherical aberration is not right but from the author's point of view this argument is not correct because he made this interpretation based on the shape of the curve around the zero mean circle. However, as mentioned, the actual interpretation of the mod must be based on the best focus, which is the interpretation given in the text.