Abstract
Background:
Sonolysis a method that uses advanced oxidation processes (AOPs), which remove organic contaminants without producing secondary waste.Objectives:
The aim of this study was to develop an empirical kinetics model to predict apseudo-first order rate constant (kap) of sonochemical degradation of malachite green (MG). Then, this model was used to estimate the required electrical energy per order (EEO) at various operational conditions.Materials and Methods:
An ultrasonic bath with the operating frequency of 35 kHz and an output power of 170 W was used for sonochemical degradation of MG. The MG concentration was determined using a spectrophotometer at 617 nm.Results:
The experimental data showed that the degradation of MG in this process obeyed pseudo-first order kinetics. Using nonlinear regression analysis a model was developed for apseudo-first order constant (kap) of the MG sono-degradation as a function of operational parameters, including initial concentration of MG (5 - 10 m gL-1), temperature (294 - 307 K), power density (0.049 - 0.163 W mL-1) and mechanical agitation (75 - 400 rpm), as shown in the Equation 3.Conclusions:
The present research demonstrated that the ultrasonic (US) process can be utilized as an effective and simple method for treatment of MG dye in an aqueous solution. Moreover, the EEO is directly proportional to the MG concentration and power density and inversely proportional to temperature and mechanical agitation, which can be predicted by the obtained empirical kinetics model. Consequently, EEO is very sensitive to the mentioned operational parameters.Keywords
Kinetics Nonlinear Regression Sonochemical Degradation Electrical Energy Per Order Malachite Green
1. Background
Environmental sonochemistry is an example of advanced oxidation processes (AOPs) and deals with the removal of toxic and hazardous organic compounds from contaminated waters (1, 2). Textile industry wastewaters have considerable amounts of organic dyes, which are resistant to conventional biological treatments. Furthermore, other physical and chemical processes, such as adsorption and coagulation, merely transfer contaminants to a secondary phase that requires more treatment. The advantages of using ultrasound are based on simplicity of its use, producing no secondary waste and good penetration of ultrasonic waves in non-transparent solutions (3-8).
Malachite green (MG) is used as an agent for food coloring, an additive to food, an anthelminthic, medical disinfectant and also as a dye in the silk, leather, cotton, paper, acrylic and textile industries. However, MG has become a highly controversial compound recently, owing to the risks it creates to those who consume treated fish, including its influences on the reproductive and immune system and its carcinogenic and genotoxic properties. The use of MG has been forbidden in several countries; for instance, it is not approved by the U.S. Food and Drug Administration. However, it is still being used in the world because of its low cost, availability and efficacy (9-11).
Cavitation is the origin of sonochemical effects, creating micro bubbles. After ultrasonic waves enter in to a liquid, the cavitation phenomenon results in formation, growth, and eventually collapse of micro bubbles generating highly localized temperatures and pressures (hot spot approach). Hence, intense energy is available for chemical and mechanical effects in the solution.
The generated reactive oxygen species from the dissociation of water molecules under ultrasonic irradiation, especially hydroxyl radicals, have the main role of degradation and mineralization of various organic contaminants such as the dyes. In the hot spot model, three regions exist including the gaseous nuclei, the interfacial regions and the bulk solution, which are dependent on the pollutant type. The degradation can occur mainly in a particular region (12-15).
Various models have been developed for description of the sonochemical process mechanism, based on the pseudo-first order kinetics assumption. Moreover, development of a kinetics model for a process based on intrinsic elementary reactions is one of the best methods, due to the exact understanding of the reactions in the process and the effects of operational parameters. However, sometimes this kind of modeling is difficult owing to the diversity of reactions, especially for a complicated process. Thus, an empirical kinetics modeling of the process via non-linear regression analysis can be applied in such cases. The validity of this empirical model was evaluated by comparison of experimentally and theoretically calculated data (16-20).
2. Objectives
The objective of the present study was to develop an empirical kinetics model to predict apseudo-first order rate constant (kap) of the MG sono-degradation as a function of initial concentration of dye [MG0], temperature (T), power density (P/V) and mechanical agitation (MA) using non-linear regression analysis. Finally, this model can be used in order to determine the required electrical energy (EEO) for the process at different operational conditions.
3. Materials and Methods
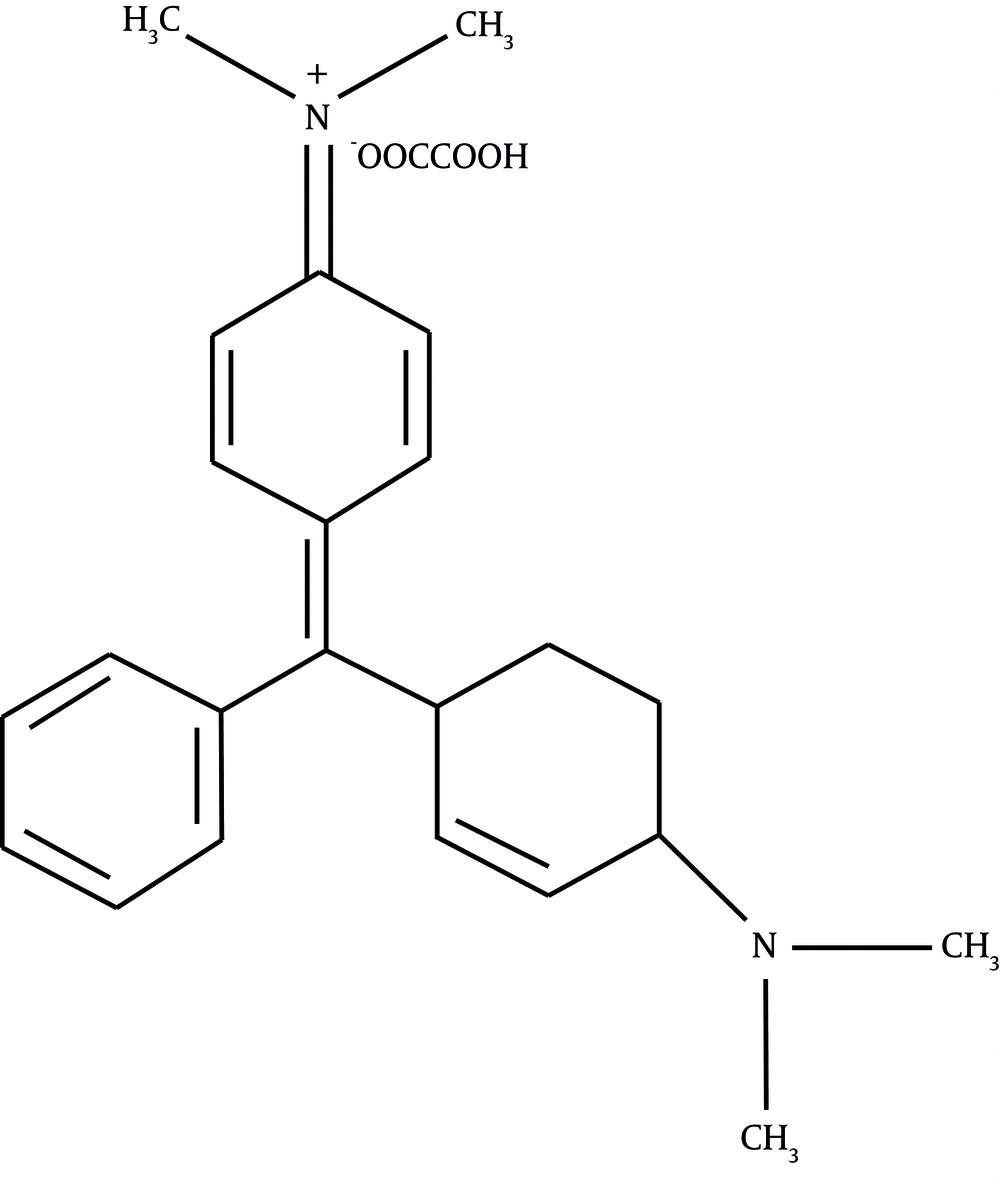
Malachite green oxalate (C.I. 42000), whose structural formula is shown in Figure 1, was obtained from Panreac Co. (Spain) and used without further purification. All solutions were prepared with double-distilled water by dissolving the required amount of MG. The ultrasonic bath was purchased from Elma (GmbH) with an operating frequency of 35 kHz and with a rated output power of 170 W. The efficiency of the bath was determined by the calorimetric method as 28.8%, which indicates that the actual power (P) dissipated in the bulk solution is 49 W (13). Power density was calculated by dividing the actual power dissipated in the bulk solution to the volume of the dye solution. Mechanical agitation was used during the experiments. The operational conditions of the experiments have been summarized in Table 1. In each experiment, a specific volume of the MG solution, with a specific concentration, was poured into the ultrasonic bath. A mechanical stirrer was used in the solution, and the sonication was started. At distinct reaction intervals, 5 mL of the sample was withdrawn and the concentration of MG was determined by the spectrophotometry method using a spectrophotometer (Ultrospec 2000, Biotech Pharmacia, England) at 617 nm.
Chemical Structure of MG
Operating Conditions of Experiments
| Operational Parameters | Values |
|---|---|
| MG initial concentration, m gL-1 | 4.89 - 9.87 |
| Temperature, K | 294 - 307 |
| Power density, W mL-1 | 0.049 - 0.163 |
| Mechanical agitation, rpm | 75 - 400 |
4. Results
The apparent rate constants (kap) of MG degradation were estimated using the pseudo-first order kinetics assumption from the slope of ln ([MG]o/[MG]) versus irradiation time at different operational conditions (13). In all cases, the R2 (correlation coefficient) values were higher than 0.99, which confirmed the proposed pseudo-first order kinetics for the process.
The relationship between kap and the initial concentration of MG, power density and mechanical agitation can be modeled with the power law-type of empirical Equations, which have the general form of:
Using nonlinear regression analysis with Polymath 5.1, model parameters were calculated and reported, and are shown in Table 2. In addition, the dependence of kap on temperature can be calculated from the Arrhenius Equation and activation energy (Ea) was 30.95 kJmol-1 (13). Therefore, kap can be modeled as the following Equation:
Model Parameters for Predicting kap
| Operational Parameters | A | Q | R2 |
|---|---|---|---|
| MG Initial concentration, m gL-1 | 0.0463 | 0.948 | 0.999 |
| Power density, W mL-1 | 0.0505 | 0.547 | 0.983 |
| Mechanical agitation, rpm | 0.0022 | 0.307 | 0.999 |
With known values of [MG]0 (m gL-1), (P/V) (W mL-1), (MA) (rpm) and T (K), we can calculate k0 as 15.75 × 103. Substituting these values into Equation 2, we obtained:
The results of this work are similar to the information found in the literature. Kim et al. (4) have reported the value of m as -1.87 for sonochemical degradation of dibenzothiophene in the initial concentration range of 3.3 × 10-6 to 7.7 × 10-6 M. Furthermore, Sivakumar and Pandit (7) found the value of power density to be 0.6418 for the degradation percent of Rhodamine B with four different ultrasonic systems. Also, for sonochemical decomposition of dibenzothiophene in aqueous solution, the activation energy was 12.6 kJ mol-1, in the temperature range of 288 - 323 K (4).
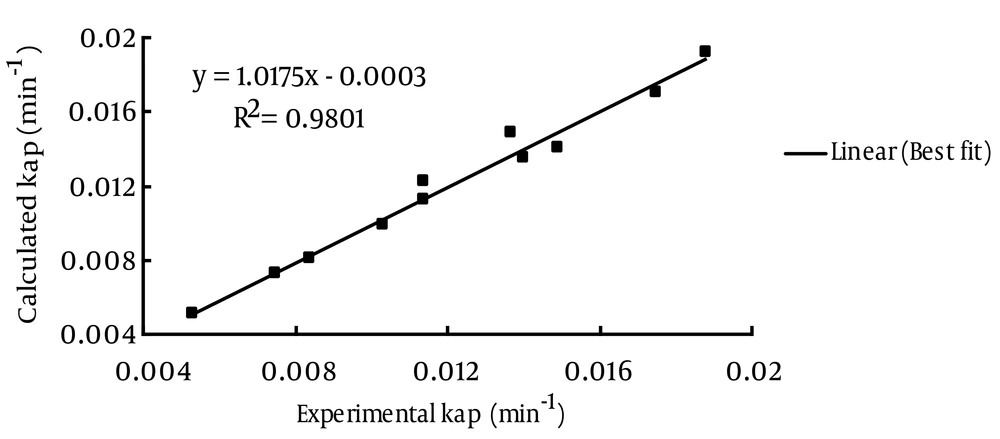
For evaluation of Equation (3) in predicting kap in different conditions, a comparison between experimental and calculated kap for sonochemical degradation of MG is shown in Figure 2.
Comparison Between Experimental and Calculated Pseudo-First Order Rate Constants for Decolorization of MG in U.S. Process at Different Operational Parameters
For experimental details refer to Table 3.
Experimental and Calculated Amounts for EEO
| Operational Parameters Variation | EEO (Experimental) | EEO (Calculated) |
|---|---|---|
| MG initial concentration (m gL-1)a | ||
| 4.89 | 633.79 | 658.21 |
| 6.82 | 870.40 | 902.30 |
| 9.87 | 1231.70 | 1280.66 |
| Temperatureb, K | ||
| 297 | 572.63 | 581.97 |
| 302 | 438.12 | 463.84 |
| 307 | 373.03 | 383.18 |
| Power densityc, W mL-1 | ||
| 0.07 | 818.05 | 764.32 |
| 0.098 | 952.99 | 879.31 |
| 0.163 | 1157.45 | 1131.89 |
| Mechanical agitationd, rpm | ||
| 75 | 777.14 | 812.34 |
| 400 | 466.28 | 485.29 |
The EEO can be calculated from the following Equation for a batch-type reactor:
Where Pel is the input power (kW) to the AOPs system, t is the irradiation time (min), V is the volume of water (L) in the reactor and C0 and C are the initial and final pollutant concentrations, respectively (21). Assuming first-order kinetics:
A comparison between predicted EEo values estimated from kinetics modeling (Equation 3) and EEo values obtained from experimental data is shown in Table 3.
5. Discussion
MG is not a volatile compound; thus, its presence in the gas phase of a cavity is unlikely. Consequently, the major route for its degradation is oxidation by hydroxyl radicals in the interfacial area. Moreover, the applied frequency of sonication is low; hence, the collapse of bubbles is more violent. However, the delayed growth and longer collapse duration permit radical scavenging and recombination reactions at the interfacial sheath, hence, inhibiting reactive species into the bulk solution. As a result, the dye degradation is increased by adsorption on the bubble-water interface (13, 22). Then, MG, a cationic dye in the basic class, can be degraded by ultrasonic irradiation, and kap can be predicted at different operational parameters, utilizing nonlinear regression analysis to obtain the empirical kinetics model. For cost evaluation, electrical energy per order (EEO) based on experimental and calculated data was obtained. The results of this study (Table 3) show that the EEO is directly proportional to the MG concentration and power density, and inversely proportional to temperature and mechanical agitation. From Figure 2, it can be seen that the results obtained from the model (Equation 3) are in good agreement with the experimental data.
As mentioned previously, the main route for MG degradation is the oxidation by hydroxyl radicals in the interfacial area; the MG degradation is limited by the available interfacial area generated at the constant sonication condition (5, 22). An explanation of the effect of power density on EEO seems to be necessary. Although kap increases with enhancement of power density, the solution volume becomes lower in the high power densities than in the low power densities. The effect of decreasing of volume is predominantly seen in Equation 5, and the EEO becomes low with enhancement of power density. The increase in temperature will raise the vapor pressure and so cause easier cavitation but less violent collapse; in this temperature range, the influence of easier cavitation is predominant. The influence of sonication on sono-degradation of MG was enhanced by mechanical stirring, owing to the dispersion of the cavitation bubbles and easier diffusion of the dye to the interfacial area (13).
Goel et al. (23) have reported EEO values for ultrasonic degradation of trichloroethylene, toluene, styrene and eosin B in aqueous solution with an initial concentration of 50 mgL-1 in an ultrasonic bath (100 W) as 4,382; 6,643; 7,538 and 7,532 kWh per m3 per order, respectively. In our work, EEO values for ultrasonic degradation of MG with an initial concentration of 5 mg L-1 in an ultrasonic bath (170 W) at different operational parameters changed from 373 to 1,232 kWh per m3 per order. The low EEO and the difference between our data and the other studies could be related to the difference in the experimental set-up of the ultrasonic bath, such as the mechanical stirrer, direct dissipation of ultrasonic waves to the solution and also various operational conditions.
Acknowledgements
References
-
1.
Adewuyi YG. Sonochemistry: Environmental Science and Engineering Applications. Indust Engin Chem Res. 2001;40(22):4681-715. https://doi.org/10.1021/ie010096l.
-
2.
Voncina D. Reactive dye decolorization using combined ultrasound/H2O2. Dyes and Pigments. 2003;59(2):173-9. https://doi.org/10.1016/s0143-7208(03)00101-3.
-
3.
Dukkanci M, Gunduz G. Ultrasonic degradation of oxalic acid in aqueous solutions. Ultrason Sonochem. 2006;13(6):517-22. [PubMed ID: 16352455]. https://doi.org/10.1016/j.ultsonch.2005.10.005.
-
4.
Kim IK, Huang CP, Chiu PC. Sonochemical decomposition of dibenzothiophene in aqueous solution. Water Res. 2001;35(18):4370-8. https://doi.org/10.1016/s0043-1354(01)00176-2.
-
5.
Manousaki E, Psillakis E, Kalogerakis N, Mantzavinos D. Degradation of sodium dodecylbenzene sulfonate in water by ultrasonic irradiation. Water Res. 2004;38(17):3751-9. [PubMed ID: 15350427]. https://doi.org/10.1016/j.watres.2004.06.002.
-
6.
Rehorek A, Tauber M, Gubitz G. Application of power ultrasound for azo dye degradation. Ultrason Sonochem. 2004;11(3-4):177-82. [PubMed ID: 15081977]. https://doi.org/10.1016/j.ultsonch.2004.01.030.
-
7.
Sivakumar M, Pandit AB. Ultrasound enhanced degradation of Rhodamine B: optimization with power density. Ultrason Sonochem. 2001;8(3):233-40. https://doi.org/10.1016/s1350-4177(01)00082-7.
-
8.
Vinodgopal K, Peller J, Makogon O, Kamat PV. Ultrasonic mineralization of a reactive textile azo dye, remazol black B. Water Res. 1998;32(12):3646-50. https://doi.org/10.1016/s0043-1354(98)00154-7.
-
9.
Culp S, Beland F. Malachite Green: A Toxicological Review. Int J Toxicol. 1996;15(3):219-38. https://doi.org/10.3109/10915819609008715.
-
10.
Alderman DJ, Clifton-Hadley RS. Malachite green: a pharmacokinetic study in rainbow trout, Oncorhynchus mykiss (Walbaum). J Fish Dis. 1993;16(4):297-311. https://doi.org/10.1111/j.1365-2761.1993.tb00864.x.
-
11.
Bergwerff AA, Scherpenisse P. Determination of residues of malachite green in aquatic animals. J Chromatography B. 2003;788(2):351-9. https://doi.org/10.1016/s1570-0232(03)00042-4.
-
12.
Behnajady MA, Modirshahla N, Tabrizi SB, Molanee S. Ultrasonic degradation of Rhodamine B in aqueous solution: influence of operational parameters. J Hazard Mater. 2008;152(1):381-6. [PubMed ID: 17723264]. https://doi.org/10.1016/j.jhazmat.2007.07.019.
-
13.
Behnajady MA, Modirshahla N, Shokri M, Vahid B. Effect of operational parameters on degradation of Malachite Green by ultrasonic irradiation. Ultrason Sonochem. 2008;15(6):1009-14. [PubMed ID: 18442946]. https://doi.org/10.1016/j.ultsonch.2008.03.004.
-
14.
Eskandarloo H, Badiei A, Behnajady MA, Ziarani GM. Ultrasonic-assisted sol-gel synthesis of samarium, cerium co-doped TiO2 nanoparticles with enhanced sonocatalytic efficiency. Ultrason Sonochem. 2015;26:281-92. [PubMed ID: 25682738]. https://doi.org/10.1016/j.ultsonch.2015.02.001.
-
15.
Eskandarloo H, Badiei A, Behnajady MA, Ziarani GM. Ultrasonic-assisted degradation of phenazopyridine with a combination of Sm-doped ZnO nanoparticles and inorganic oxidants. Ultrason Sonochem. 2016;28:169-77. [PubMed ID: 26384896]. https://doi.org/10.1016/j.ultsonch.2015.07.012.
-
16.
Behnajady MA, Vahid B, Modirshahla N, Shokri M. Evaluation of electrical energy per order (EEO) with kinetic modeling on the removal of Malachite Green by US/UV/H2O2 process. Desalination. 2009;249(1):99-103. https://doi.org/10.1016/j.desal.2008.07.025.
-
17.
Khataee A, Vahid B, Behjati B, Safarpour M, Joo SW. Kinetic modeling of a triarylmethane dye decolorization by photoelectro-Fenton process in a recirculating system: Nonlinear regression analysis. Chem Eng Res Des. 2014;92(2):362-7. https://doi.org/10.1016/j.cherd.2013.07.019.
-
18.
Khataee A, Vahid B, Saadi S, Joo SW. Development of an empirical kinetic model for sonocatalytic process using neodymium doped zinc oxide nanoparticles. Ultrason Sonochem. 2016;29:146-55. [PubMed ID: 26584992]. https://doi.org/10.1016/j.ultsonch.2015.09.004.
-
19.
Okitsu K, Iwasaki K, Yobiko Y, Bandow H, Nishimura R, Maeda Y. Sonochemical degradation of azo dyes in aqueous solution: a new heterogeneous kinetics model taking into account the local concentration of OH radicals and azo dyes. Ultrason Sonochem. 2005;12(4):255-62. [PubMed ID: 15501707]. https://doi.org/10.1016/j.ultsonch.2004.01.038.
-
20.
Samaei MR, Maleknia H, Azhdarpoor A. Effects of pH on the Kinetics of Methyl Tertiary Butyl Ether Degradation by Oxidation Process (H 2 O 2/Nano Zero-Valent Iron/Ultrasonic). Jundishapur J Health Sci. 2015;7(3). ee30285.
-
21.
Bolton JR, Bircher KG, Tumas W, Tolman CA. Figures-of-merit for the technical development and application of advanced oxidation technologies for both electric- and solar-driven systems (IUPAC Technical Report). Pure Appl Chem. 2001;73(4):627-37. https://doi.org/10.1351/pac200173040627.
-
22.
Ince NH, Tezcanli-Guyer G. Impacts of pH and molecular structure on ultrasonic degradation of azo dyes. Ultrasonics. 2004;42(1-9):591-6. [PubMed ID: 15047352]. https://doi.org/10.1016/j.ultras.2004.01.097.
-
23.
Goel M, Hongqiang H, Mujumdar AS, Ray MB. Sonochemical decomposition of volatile and non-volatile organic compounds--a comparative study. Water Res. 2004;38(19):4247-61. [PubMed ID: 15491671]. https://doi.org/10.1016/j.watres.2004.08.008.