1. Introduction
“A clinical practise guideline (CPG) is a set of recommendations or rules developed in some systematic way in order to help professionals and patients during the decision-making process concerning an appropriate health-care pathway, by means of opportune diagnosis and therapy choices, on specific health problems or clinical conditions” (1). CPGs are designed by specialists to be used by all clinicians in a country or all over the world. A CPG is considered as a standard for the diagnosis and treatment of a disease. Therefore, the logical consistency of a guideline is crucial, and designers must ensure the consistency of a guideline prior to use by clinicians.
Usually, a CPG is written in a natural language. Since CPGs are complex, designing them is a difficult and error-prone task and may have some ambiguity due to the nature of a natural language. As a result, having an appropriate formal language to model and analyze CPGs helps clinicians to reduce errors and resolve ambiguity issues. Moreover, designers can use some tools developed for the language to easily model a guideline and check its logical consistency with no trouble.
There are different formalizations and tools with different functionalities [e.g., Absru (2, 3), PROforma (2, 3), EON (4), GLIF (2, 3), g-HMSC (5), Little-JIL (6)]. While some of these languages are considered as general-purpose process modeling languages, e.g. PROforma, Little-JIL, g-HMSC, some other languages are particularly designed to model clinical guidelines (EON and GLIF). Generally, these languages are designed to reduce potential errors occurring in the process of delivering the treatment to a patient, and also to make it easier for clinicians to use guidelines for the diagnosis or treatment of a disease (2). In the next section, we briefly review these formalisms.
As it was explained in previous study (2), since a CPG is a time-oriented process that consists of treatment steps and/or diagnostic steps, which are performed in a temporal setting, a temporal logic can be used to model the CPG and support the (semi) automatic analysis. Moreover, because the domain of medicine is inherently interval-based in the sense that most activities are described as being performed in an interval, e.g. taking ibuprofen for 2 days, an interval-based temporal logic is a suitable choice to model a guideline. Furthermore, duration of most medical activities is known and must be specified in a CPG; hence, the desired formalism should be a metric one (3).
In previous studies (2, 3), we introduced a metric interval-based temporal logic called IMPNL. Moreover, we proposed a tableau-based algorithm for the satisfiability checking of an IMPNL formula. We indicated that the algorithm was sound and complete and that the complexity of the algorithm was in PSpace. We also explained that how IMPNL could be used to model a CPG and check its consistency.
In this paper, we introduced a clinical practice guideline analyzer. The newly introduced tool uses IMNPL to model a CPG and checks its consistency based on the proposed algorithm for satisfiability checking of an IMPNL formula. Notably, a CPG is consistent if a corresponding IMPNL formula is satisfiable.
The rest of the paper is organized as follows: In section 2, the existing formalisms for modeling clinical guidelines are reviewed. In section 3, the syntax and semantics of IMPNL are discussed, and a CPG analyzer is presented. Finally, the last section concludes the work and recommends future studies.
2. Background
In this section, we briefly considered the following languages which are used to model clinical guidelines. In previous study (2), we compared some of these formalisms.
Arden Syntax (4, 7) is a rule-based language aimed to be considered as a standard for representation of processes and sharing of medical knowledge; however, it is not able to model complex guidelines (7), e.g. treatment guidelines. In Arden Syntax, a medical logic can be encoded as independent rules, such as reminders and alerts (8). Two tools, i.e. Medical Logic Module Library and the MLM (Medical Logic Module) syntax checker, have been developed for this language.
EON (4, 9) is particularly designed to model medical guidelines. In this language, a complex clinical guideline is modeled as a “network of tasks”, and each task consists of some steps with a specific function or goal (6, 8). This language is powerful enough to model domain ontologies (6). The Protégé-2000 knowledge engineering environment is used for encoding EON guidelines.
Glare (10, 11) is a domain-independent system for acquiring, representing, and executing medical guidelines (12). An informal state-based semantics is defined for this language; however, it can be automatically translated to the input language of SPIN (6). Some tools have been developed for the language with the purpose of acquisition and execution of guidelines (13).
PROforma (6, 9) is a general-purpose process modeling language, and is also a task-based formalism that can model clinical processes as a collection of plans, decisions, enquires, and actions (14). PROforma contains expressive constructs for describing uncertainty aspects of a guideline. Different tools [e.g., Arezzo®, Performer, Tallis (14)] have been developed for the language to model various processes in different domains.
Little-JIL (6), as a general-purpose process modeling language, models clinical guidelines in form of a collection of tasks and supports hierarchical decomposition, decisions, goals, concurrency, and exception handling (6). One of the main advantages of the language is its exception handling mechanism, through which it separates normal flow from exceptional flow. Little-JIL provides various continuation options after handling an exception (6). It can be automatically translated to the input language of formal verifiers (6), FLAVERS (5), and SPIN (15). Therefore, it is possible to determine whether certain goals or properties are always satisfied on all possible execution paths through the process definition. In terms of support for timing issues, Little-JIL is not as strong as EON, or PROforma (6). Moreover, it has not enough manuals and documentation (16).
Asbru is a time-oriented (17), text-based, machine-readable (18), and general-purpose process modeling language. Similar to EON, the language can model complex clinical guidelines as a “network of tasks”, and each task may consist of some steps with a specific function or goal (8). Asbru can be automatically translated to an internal representation used by the SMV model checker (6, 19), and KIV (8, 20). AsbruView is a tool providing visualization and understanding of Asbru guidelines. Moreover, Asbru Interpreter is an execution engine for clinical guidelines modeled in Asbru (21).
G-HMSC (5, 22) is a formalism, in which a simple flowchart is drawn to model multi-agent processes involving decisions (5). There are some tools performing various analyses, e.g. model checking, state invariant generation, guard analysis, verification of non-functional process requirements, verification of task preconditions, and detection of inadequate decisions, on processes modeled by g-HMSC (5, 22). Hommersom et al. (23) proposed a restricted version of a point-based temporal language to formalize a guideline. They translated the language to a simple fragment of first-order logic and used OTTOR as a resolution-based theorem prover as well as MACE-2 as a program to search small finite models in first-order logic to assess the quality of guidelines by checking whether or not a property holds.
While some tools with reasoning facilities have been provided to find and fix some guideline errors (e.g., inconsistent precondition of an activity), none of them can automatically check the satisfiability of a guideline. Therefore, the main difference between these languages and our tool is the ability to automatically and easily check the satisfiability of a guideline.
3. Methods and Discussion
At first, we described a metric interval-based language called IMPNL and then we introduced the CPG analyzer.
3.1. IMPNL - A Metric Interval-Based Temporal Logic
The language of IMPNL consists of a set, AP, of propositional variables, logical operators, atomic negation (¬), or (∨), and and (∧), and temporal operators, ◊r and ◊l, corresponding to Allen’s relations meet and its inverse, met-by. This logic has two constants ⊤ (True) and ⊥ (False), defined as usual.
The formulas, denoted by φ, ψ, ..., are recursively defined using BNF (Backus Naur Form), where pk is a propositional variable. Notably, the subscript of an atomic formula denotes the length of the interval, on which it should be evaluated. However, the subscript of a non-atomic formula denotes an index, and is used to distinguish the formula from other formulas.
ψ = pk |¬pk |⊤k |⊥k |ψ1 ∨ ψ2 |ψ1 ∧ ψ2 |◊rψ|◊lψ where k ∈ N
In IMPNL, a user must specify the length of an interval as a subscript of a propositional variable. Therefore, it is not possible to have a propositional variable as an atomic formula without specifying the length.
The semantics of IMPNL is based on a 3-tuple structure M = ⟨D, I(D)−, V⟩, where the pair ⟨D, I(D)−⟩ is a strict interval structure and V: I(D)− → 2AP is a valuation function that assigns to every interval a set of propositional variables which are true on that interval. A satisfaction relation is defined as follows:
It is stated that a formula ψ is satisfiable if there exists a structure M and an interval [c0, c1] s.t. M, [c0, c1] ⊨ ψ. Moreover, it is easy to show that M, [i, j] ⊨ ◊z(ψ1 ∨ ψ2) if and only if M, [i, j] ⊨ ◊zψ1 ∨ ◊zψ2 (z ∈ {r, l}), and if M, [i, j] ⊨ ◊z(ψ1 ∧ ψ2), then M, [i,j] ⊨ ◊zψ1 ∧ ◊zψ2 (z ∈ {r, l}).
Notably, in IMPNL, only an atomic formula can be negated and there is no negation for a complex formula. In addition, the length of each atomic formula must be specified. Finally, IMPNL has a homogeneity assumption, i.e. if a formula is true (false) on an interval, it is true (false) in every subinterval of that interval.
3.2. CPG Analyzer
In this section, we presented our tool which uses IMPNL to model a CPG and checks its satisfiability and consistency using the tableau-based satisfiability checking algorithm for IMPNL formulas.
Our analyzer has different modules. One module is responsible for processing IMPNL and constructing the corresponding tableau tree. This module is implemented using NodeJS and C++. The client part of the analyzer, responsible for inputting formula and showing the corresponding tableau tree along with calendar and other provided information, is a web-based application.
As we already mentioned earlier, manual checking of satisfiability of a CPG is difficult, time-consuming, and error-prone. Sometimes, we need a loop in a guideline [See section 6.1 of Yousef Sanati study (2)]. To analyze such a loop, we should expand the formula and apply the algorithm on the expanded version. This needs hard work and is impossible to be performed manually. Moreover, it is crucial to detect points where inconsistencies occur. Our tool deals with all these problems. Here, we modeled a real-life guideline using our tool and showed that the CPG was consistent. Further, we described a situation, in which inconsistency points occurred. Finally, it is important to note that we developed the analyzer based on formal software engineering guidelines to have a user-friendly software. For example, a wizard helps clinicians to enter the formula and analyze it. Moreover, the analyzer’s interface is straightforward and makes sense for the majority of clinicians. In addition, the analyzer results are visualized (e.g., in the format of a tree or calendar) for clinicians and thus are more understandable.
3.3. HIV/AIDS Guideline Analysis
In this section, we modeled a real-life guideline for the diagnosis and treatment of HIV/AIDS from previous study (2). Due to the lack of space, we briefly described the guideline and refer the reader to Yousef Sanati study (2) for full details.
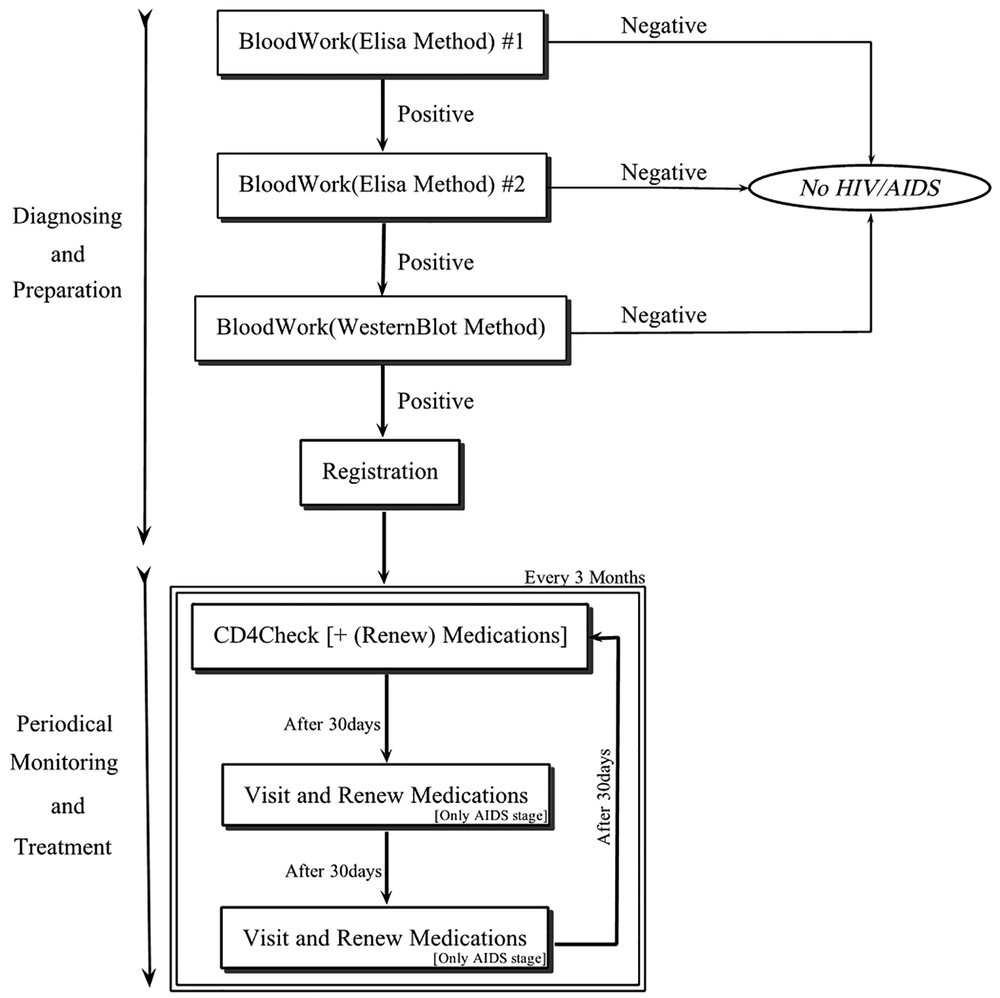
Generally, HIV/AIDS has three major stages as follows: acute infection (lasts 6 - 8 weeks), clinical latency (lasts 8 - 10 years), and AIDS (lasts 0 - 20 years). The diagnosis and treatment processes of the disease are similar for any HIV/AIDS patient in each of the stages. Figure 1 shows the entire process of the HIV/AIDS clinical practice guideline.
The HIV/AIDS CPG (2)
As can be observed in Figure 1, blood-work should be performed three times to ensure that the patient has an HIV infection. Each blood-work and registration process take 1 day and 4 days, respectively. Routinely, the blood level, of CD4 (Cluster of Differentiation 4) of an infected patient should be investigated every 3 months. If the level is fine and the patient has no sign of AIDS (e.g., Candidiasis of bronchi), no medication is needed. However, if the level is not acceptable, or there is at least one sign of AIDS, the patient should take three medications every day. Furthermore, the patient should be visited by a physician every 30 days to ensure that he/she takes the right medications with the right dosages. The prescriptions for the patient should be also renewed. Here, we considered one combination of medications, i.e. Kaletra, Tenofovir, and Lamivadin, from different possible combinations used for the treatment (2).
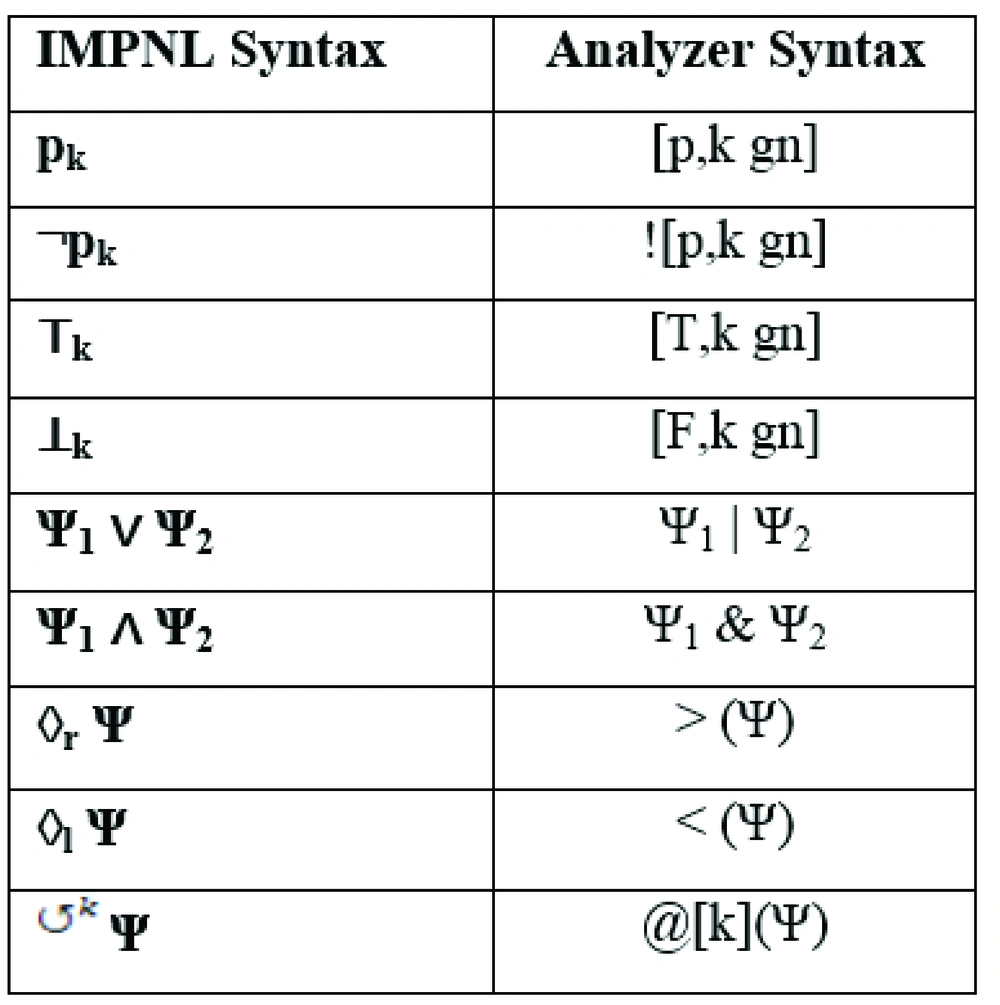
To enter a CPG formula, conventions in Figure 2 are used. Here, gn can be any granularity including d (days), mon (months), y (years), h (hours), min (minutes), and s (seconds).
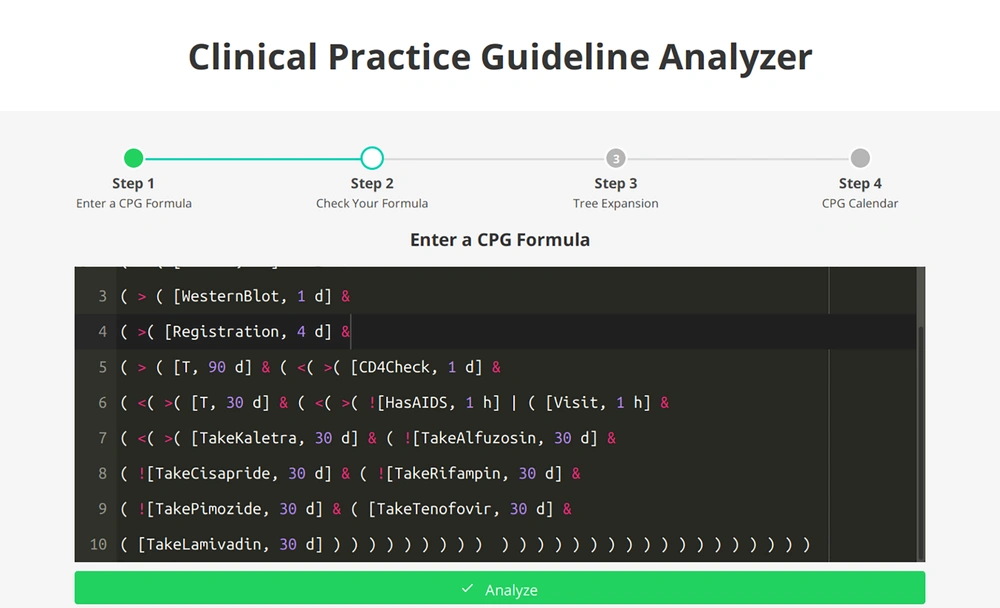
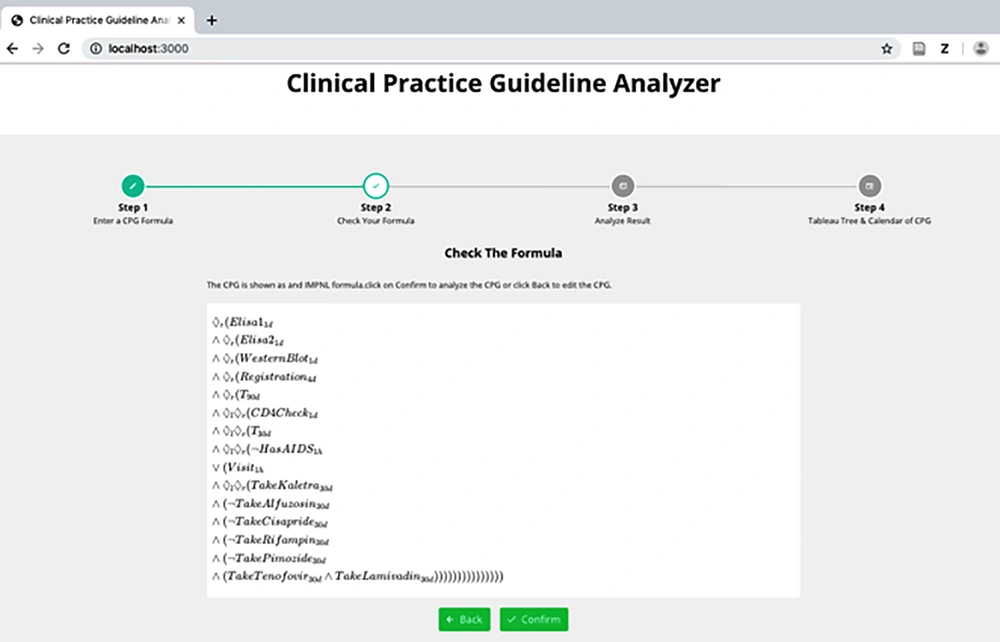
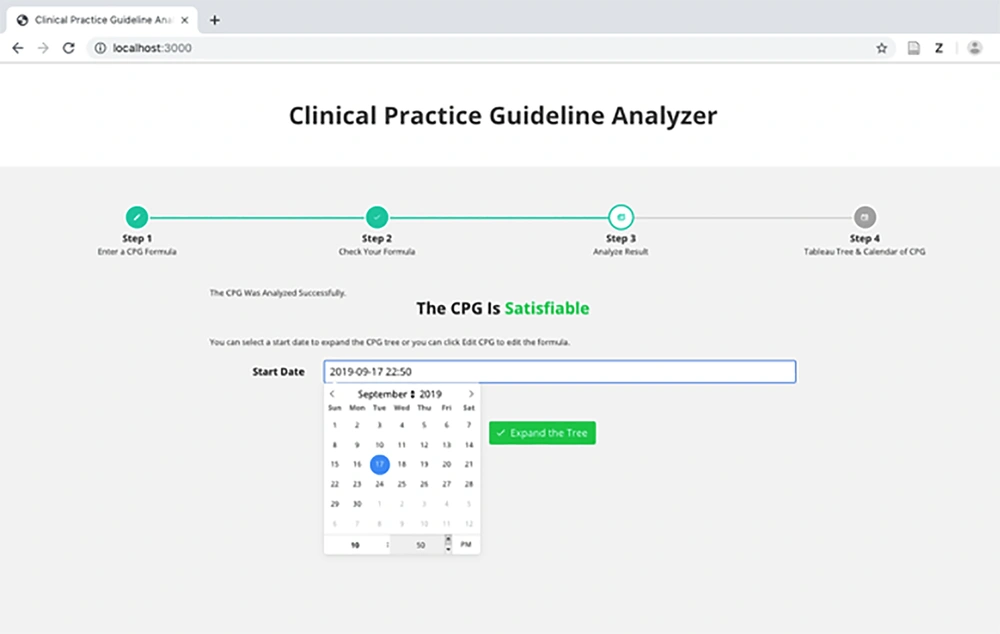
Figure 3 represents the analyzer syntax of the HIV/AIDS CPG. After the analysis, the IMPNL syntax of the formula and the result of the satisfiability of the CPG are shown in Figures 4 and 5. As can be observed in the figure, the CPG is satisfiable. This indicates that the guideline is consistent and can be used for patients.
3.4. Concrete Model of the CPG
Another important feature of the analyzer is the ability to generate a concrete model for a CPG in two forms as follows: tree model and calendar model. Whatever model is desired, the start date and time should be provided by the designer (Figure 5).
3.4.1. Tree Model
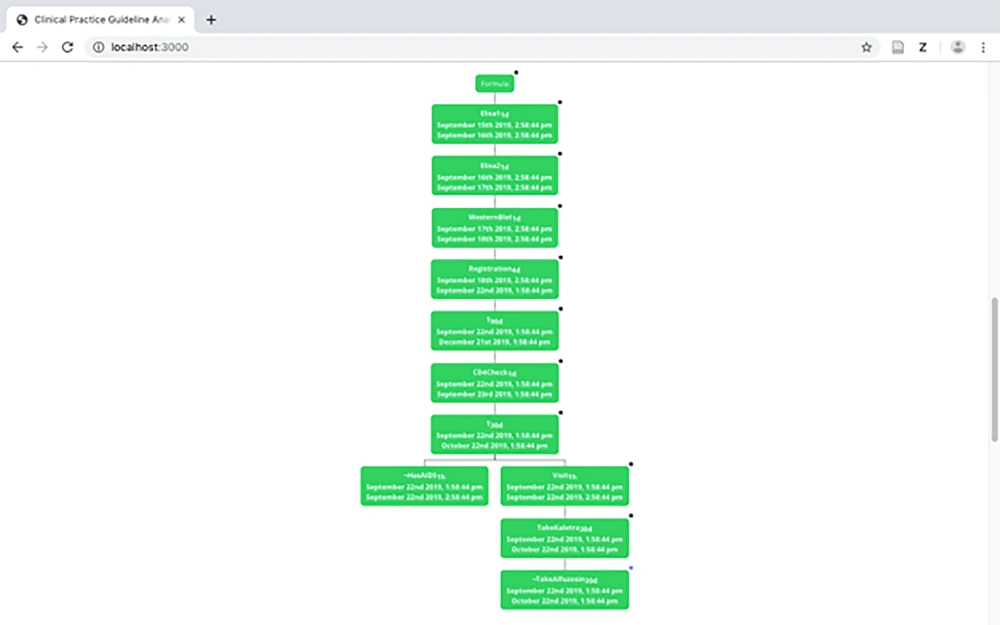
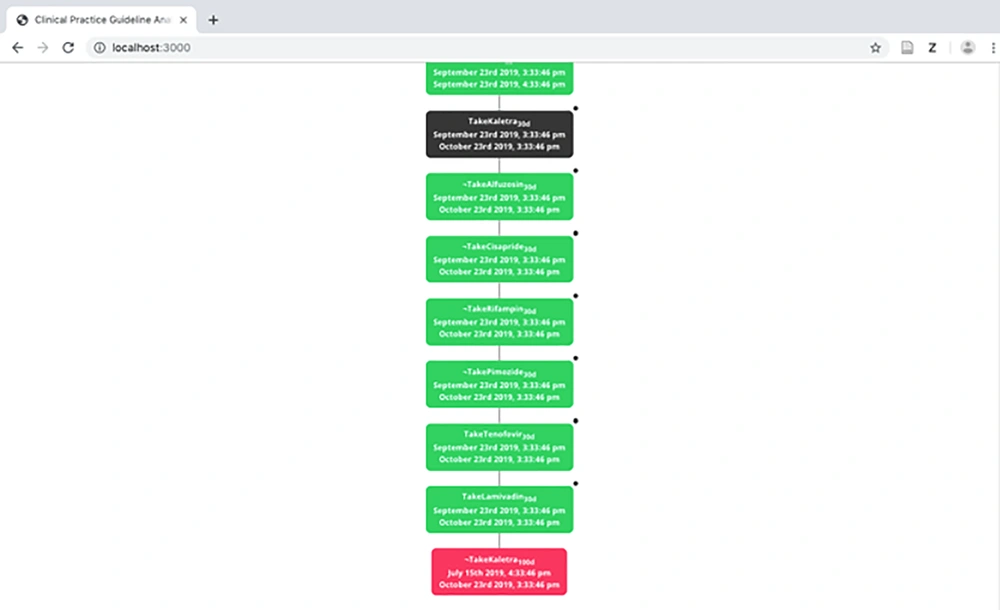
The tree model is constructed using the tableau-based algorithm presented in previous studies (2, 3). Figure 6 displays a part of the tree model of the HIV/AIDS CPG. As can be observed in the figure, two branches exist. The left branch represents the status, in which a patient is not in the AIDS stage of the disease whereas the right branch demonstrates the treatment process in the AIDS stage. Every node in the tree contains the medical activity and the interval, on which the activity should be carried out.
3.4.2. Calendar Model
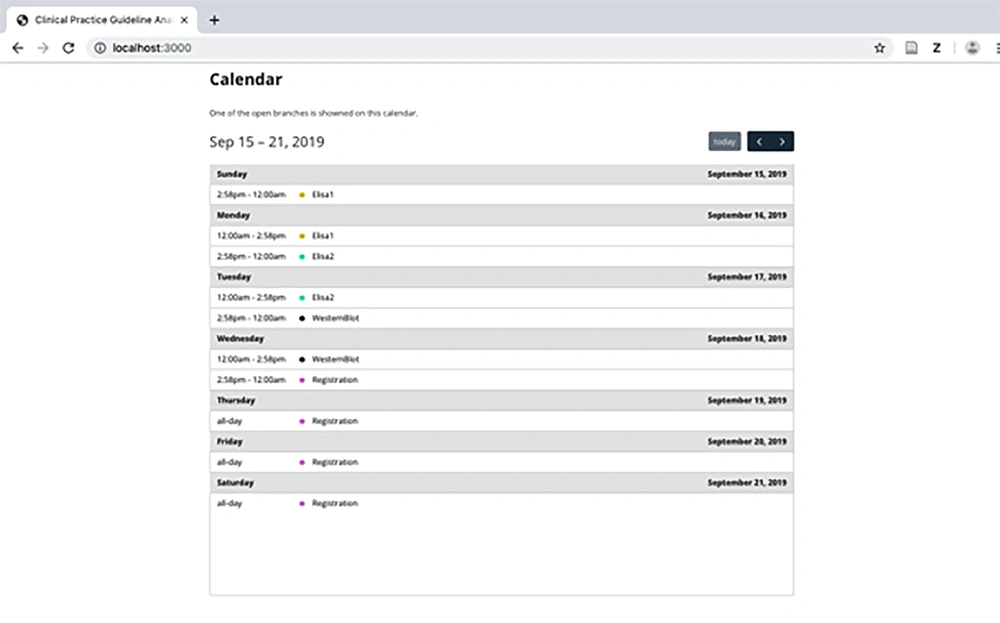
The main aim of the analyzer is to help CPG designers to check the satisfiability of a CPG; however, a physician can also use the calendar model to check whether a patient is coherently treated with the HIV/AIDS CPG (Figure 7).
Accordingly, this is a vital feature that increases the safety of the patient and prevents many medical errors.
3.5. Inconsistency Point Detection
One of the important features of the tool is the ability to help designers to easily find inconsistencies. They can use this feature to determine and fix problems.
Generally, the two following types of inconsistencies can be detected by the analyzer.
3.5.1. Medical Activity Duration Inconsistency
This type of inconsistency occurs when the duration of a medical activity is not equal to the length interval, on which the activity should be performed. As an example, the formula [TakeKaletra, 100 d] and [TakeRifampin, 30 d] is unsatisfiable, because [TakeKaletra, 100 d] and [TakeRifampin, 30 d] are inconsistent. There should be an interval, on which a patient should simultaneously take Kaletra and Rifampin for the entire duration of the interval. This is impossible since Kaletra should be taken for 100 days whereas Rifampin should be taken for 30 days.
3.5.2. Medical Activities Conflicts
During the analysis, there may be an interval, in which two conflicting medical activities should be performed. This problem must be detected and avoided by the designer during CPG designing. Suppose that there is an interval, on which Kaletra should be used and should not be used. This is an inconsistency and must be fixed by changing the CPG formula.
In the tree model, inconsistent nodes are shown in red. A designer can click on a red node and observe a hint which indicates why the medical activity corresponding to the node is inconsistent. Moreover, if there is a conflicting medical activity to this node, the node corresponding to the activity turns black. In order to show this feature, we remove ![HasAIDS, 1 h] (in IMPNL ~HasAIDS1h) from the formula and add ><(![TakeKaletra, 100 d]) (in IMPNL ◊r ◊l (~TakeKaletra100d)) to the end of it. Figure 8 illustrates inconsistent nodes (red and black nodes).
4. Results and Conclusion
In this paper, we introduced a CPG analyzer based on a tableau-based algorithm for satisfiability checking of a metric interval-based temporal logic called IMPNL. At first, we reviewed the syntax and semantics of a metric interval-based temporal logic. Then, we presented the CPG analyzer. Designers can use the analyzer to model CPGs and check whether CPGs are satisfiable. In other words, if there are any inconsistent conditions in the guideline, the analyzer can determine that the guideline is not satisfiable. Moreover, the analyzer highlights points where inconsistencies occur. Accordingly, this helps designers to find and fix inconsistencies. Another important feature of the analyzer is the ability to generate a concrete model for a guideline. As a future work, we are going to develop an enhanced CPG analyzer based on MITDL (Metric Interval-based Temporal Description Logic), which is considered as a metric interval-based temporal description logic language. MITDL is a combination of IMPNL with the description logic ALC (Attributive Concept Language with Complements). This logic is powerful enough to model both dynamic (e.g., time constraints) and static (e.g., drug contraindications) aspects in the domain of medicine.