1. Background
Thyroid diseases are among the most common endocrine disorders worldwide. The thyroid is a small, butterfly-shaped gland that lies in the middle of the lower neck. Thyroid disorders include thyroid benign and cancerous nodules. Deficiency and abnormal hypersecretion of thyroid hormones are termed hypothyroidism and hyperthyroidism, respectively. Levothyroxine is a drug of choice in hypothyroidism, whereas hyperthyroidism is controlled by antithyroid drugs, which reduce the synthesis of thyroid hormones, or decreasing the thyroid tissue amount with radioiodine (131I) treatment or thyroidectomy (1). The exact description of thyroid hormones is not found in the ancient literature of Unani medicine. However, Jalinoos was the first physician to describe the anatomy of the thyroid gland (2). Ancient Unani physicians treated thyroid disorders with seaweed, which contains a high amount of iodine and advised heated sponge for goiter (3).
Symptoms of thyroid disease are easily confused with those of the other illnesses that can make the diagnosis difficult. Once thyroid disease is gotten initially, the disorder can be monitored even before starting the treatment. Early and cost-effective diagnosis and treatment of thyroid disorders is a challenge in both Unani and modern medicine.
Physicians’ diagnosis dataset and disease grouping methods are valuable in medical diagnosis for experts. Grouping methods can minimize fault diagnosis rates that may happen to low-experience physicians, and the results can be achieved in the short-run (4).
Artificial neural networks (ANNs) (5) are applied in many researches in various medical fields. ANNs are also used to classify thyroid diseases. Keleş and Keleş (6) studied the thyroid disease diagnosis for the first time and introduced an expert system according to the neuro-fuzzy classifier with 95.33% accuracy. Temurtas (7) conducted a study on designing a model for thyroid disease diagnosis with 93.19% accuracy using the multilayer perceptron (MLP) and Levenberg-Marquardt (LM). The study by Chen et al. (8) on thyroid disease suggested a particle swarm optimization (PSO) that optimized support vector machines with the fisher score (FS-PSO-SVM) CAD system and an average accuracy of 97.49%. Razia et al. (9) used the UCI dataset to compare MLP and radial basis function performances. Ma et al., (10, 11) proposed a convolutional neural network according to the computer-aided diagnostic method for thyroid diseases using the single-photon emission computerized tomography (SPECT) images.
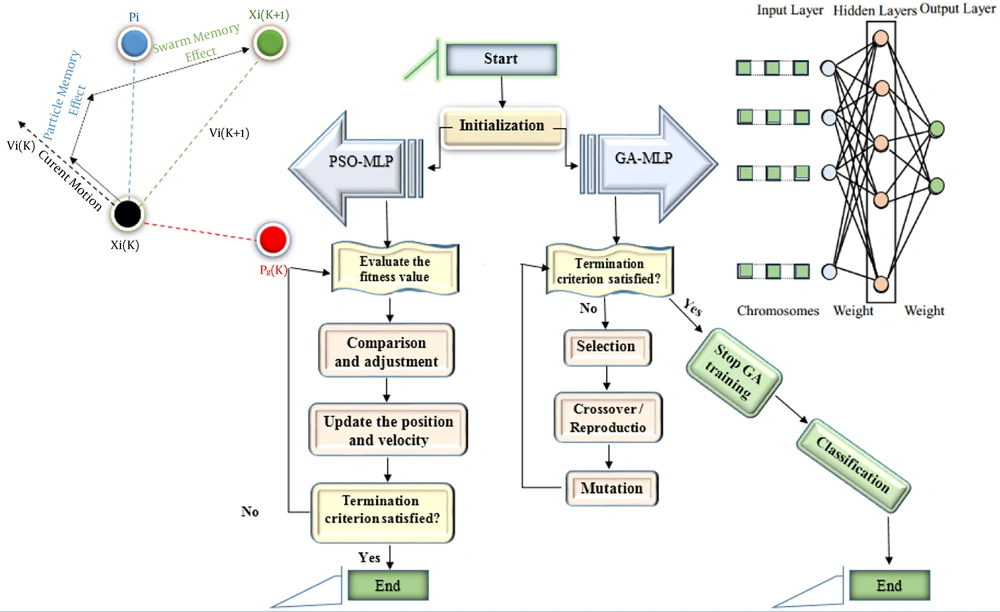
Based on the stated researches, it is assumed that the unique capability of ANNs can be efficient and useful to categorize, differentiate, and diagnose diseases. In the current study, it was attempted to diagnose the disease with simple parameters through chemometric methods using MLP. The PSO and genetic algorithm (GA) techniques optimizing models were used to diagnose thyroid functional disease. The overall suggested framework of algorithms is illustrated in Figure 1.
The framework of combining particle swarm optimization and the genetic algorithms as training of multi-layer perceptron technique for classification
2. Objectives
The current study aimed at investigating the early diagnosis of acute kidney disease by increasing the accuracy of diagnosis using the MLP method to reduce the duration and cost of treatment.
3. Methods
3.1. Data
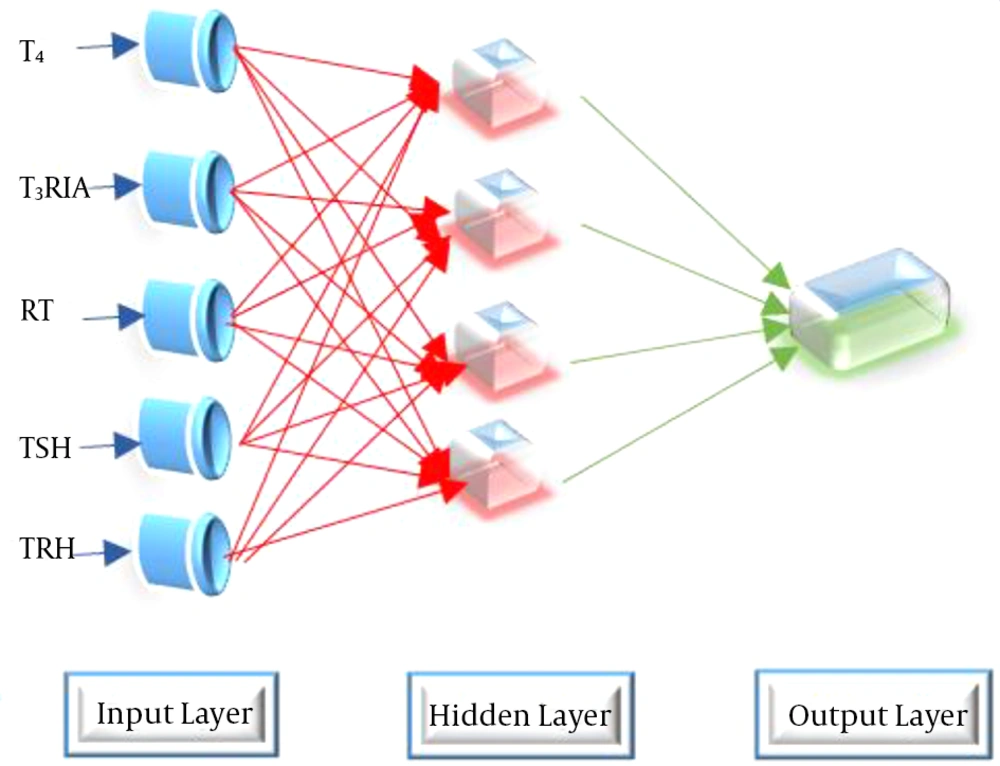
The current study used the dataset including the results of five laboratory tests regarding the thyroid gland from the UCI machine learning repository as follows: total serum thyroxin (T4), the maximal absolute difference (∆TSH), T3-resin uptake test (RT3U), total serum triiodothyronine (T3RIA), and basal thyroid-stimulating hormone (TSH) (12). The data were collected for three classes: 150 cases of euthyroidism, 30 cases of hypothyroidism, and 35 cases of hyperthyroidism. The diagnoses were based on a complete medical record, including scan images, anamnesis, etc. The input, hidden, and output layers of NN to diagnose thyroid functional disease are demonstrated in Table 1.
| Layers | Details | |
|---|---|---|
| Input layer | Factors | T4 |
| T3RIA | ||
| RT3U | ||
| TSH | ||
| TRH | ||
| Hidden layer(s) | Number of hidden layers | 1 |
| Output layer | Dependent variables | Displacement |
| Number of units | 1 | |
| Rescaling method for scale dependents | Standardized | |
| Activation function | Identity | |
| Error function | Sum of squares | |
Neural Network Input, Hidden, and Output Layers Structure for Diagnosis of Thyroid Functional Disease
3.2. Multilayer Perceptron
ANNs are utilized in innovation and science in biology, chemistry, and physics. An ANN is the human neural architecture mathematical representation reflecting its learning and generalization abilities (13). The ANN basic architecture applied to implement this classification task is a supervised network of multilayer feed-forward with the algorithm of backpropagation learning (14). The training and testing algorithm was coded using the basic MATLAB in order to analyze the data.
The MLP includes interconnected neurons or nodes in a simple system (Figure 2), which is a model among an input and an output vector representing a nonlinear mapping. The nodes can be viewed as weighted directed graphs and generate an output signal, which is a function of the sum of the inputs to the modified node by a simple nonlinear transfer or activation function.
The architecture of a general three-layer neural network with one hidden layer and one output
A typical MLP network of processing nodes comprises at least three layers: an input layer that gets external inputs, at least one output layer, and a hidden layer that creates the classification. MLP is a prominent NN model owing to its comparably simple algorithm and the clear architecture. Due to the variety of NN training methods, choosing the most optimal training method can increase the accuracy of NN predictions. The current study employed three algorithms to train NN: the Levenberg-Marquardt algorithm, PSO, and GAs.
3.3. Particle Swarm Optimization
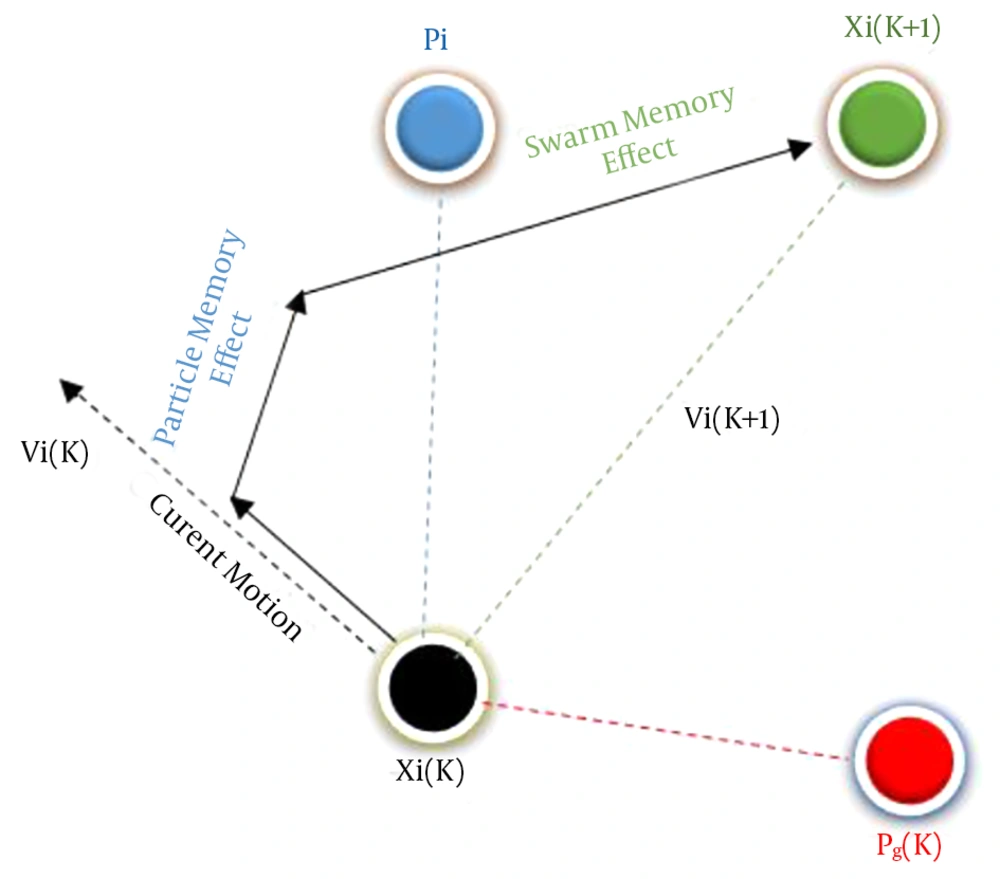
PSO is a populace-based stochastic streamlining procedure introduced by Kennedy and Eberhart (15), propelled by social conduct of bird flocking or fish schooling, in which every person is treated as a minuscule particle in the n-dimensional space, with the velocity vector of particle i and position vector demonstrated as Xi(t) = (Xi1(t), Xi2(t), …, Xin(t)) and Vi(t) = (Vi1(t), Vi2(t), ...,Vin(t)). The particles travel as indicated by the following formula:
where acceleration coefficients including c1 and c2 and particle i are recognized as the personal best position (pbest), which is the best previous position (the position providing the best value of fitness) shown as vector Pi = (Pi1, Pi2, …, Pin), and the global best position (gbest) is the best position between the particles individual best positions in the populace demonstrated as vector Pg = (Pg1, Pg2, ..., Pgn).
Two random numbers uniformly dispersed in (0, 1) are r1 and r2. Commonly, the Vid value is constrained in the interval [-Vmax, Vmax]. Shi and Eberhart introduced inertia weight w, generally applied to accelerate the algorithm convergence speed (16, 17).
In PSO, in the swarm, every particle demonstrates a point in the solution space. The particles move around the space to find the optimum solution while thinking about the best solution (point) attended using the entire swarm and using the individual. X, inertia weight is another significant parameter that adjusts the ability of algorithm local search and the global search. The large inertia weight values increase the global search algorithm. Once the algorithm converges to the optimum solution, it can be considered as a disadvantage to select a large value for the inertia weight. Hence, strategies are offered to alter the inertia weight (17, 18) adaptively. Regarding the classification and performance, a constant inertia weight was utilized in the current study. The PSO algorithm diagram is demonstrated in Figure 3.
The diagram of the PSO algorithm
3.4. Genetic Algorithms
GA is a technique of global search applied in the computational approach classified as a heuristic one (19). GA is a search technique to find approximate solutions to optimization problems. Therefore, it is not ensured to get the optimal solution. It is a global search procedure obtained and meant for proficient search and plan techniques. Three essential genetic operators manage the current exploration: mutation, selection, and crossover. GAs utilize these systems to locate an ideal explication for any multidimensional issue (20, 21). GA is a particular class of evolutionary algorithms (also recognized as evolutionary computation), which utilizes methods enlivened by evolutionary biology, including crossover, selection, mutation, and inheritance. Lately, the inclination to hybridize ANN and GA is common among authors (22-25). The preferences suggested by the current procedures shape a preferable GA-ANN hybrid intelligence framework, which could promote speculation and, in the meantime, facilitate the ANN configuration procedure.
3.5. Data Cleaning and Preprocessing
The database should be preprocessed before assessment by the NN data in training. For this purpose, a few methodologies are available. To lie within the interval (0, 1), data are commonly scaled according to the most usually utilized transference function, which is the so-called logistic one. Furthermore, it is exhibited that instances of missing information ought to be expelled from the database to enhance the characterization accomplishment of the system (26). A reduction in the network performance classification is observed for the database that is imbalanced, the ones with various number cases for any class (27).
3.6. Software
The PSO and GAs, as training for the MLP models, were calculated by classification toolbox 4.0 in MATLAB environment (MATLAB R2018a, The Mathworks Inc., Natick).
4. Results
The designed network has just one output neuron, similar to the current study, figured as a binary categorizing issue once the three classes are 2, 1, and 0. In the current study, five inputs were selected and viewed as elements to predict thyroid functional disease. The inputs were based on thyroid functions: the isotopic displacement method by which T4 was measured within 5.2 - 11.6 µg/dL as the normal range; radioimmunoassay by which T3RIA was measured within 0.8 - 2.5 µg/L as the normal range, radioimmunoassay by which RT3U was measured within 94% - 118% as the normal range, TSH calculated within 0.3 - 2.5 µIU/mL as the normal range; and ∆TSH was the 5th variable in which the TSH value maximal absolute difference after the injection of 200 µg TRH was compared with that of the basal value.
The study employed a feed-forward MLP with one hidden layer. Then the Levenberg-Marquardt algorithm was used to train the MLP. Furthermore, the NN initial weights and bias were defined by PSO and GA. Last but not least, the weights and bias in each layer were coded in sequence in PSO and GA. After designing the network data processing by the ANN technique, training and testing were the two key phases. To implement the algorithm, no standard NN software was applied; rather, the basic MATLAB was employed. The normalized inputs were fed into the network to train the NN until the network was given adequately small goal mean squared error (MSE). In the current study, a fully-connected feed-forward NN with one hidden layer was applied.
5. Discussion
All 215 individuals with the five features mentioned in these algorithms participated in the study, and data of 70% of them were selected as training, 10% as validation, and 20% as test results. To achieve the best classification, different architectures for NN were used; 4 - 20 neurons in the middle layer and weight optimization of the features through all three algorithms in 400 Epoch. The MSE index was used as the performance indicator calculation, and the best model for each algorithm was reported. In case of no improvement in fitness values after 40 Epoch, the algorithm was stopped.
An expert diagnostic system based on the comparison of PSO with GA as training for MLP technique classifier was introduced to diagnose thyroid functional disease. The results mentioned above for the problems of the thyroid functional disease classification confirmed that the network diagnoses thyroid functional disease with the 95% performance of the network, as demonstrated in Table 2. The significance of each term was determined by P- and R% values. The smaller the P value and the larger the R% value, the more significant is the corresponding term. The results of the analysis of variance (ANOVA) in the diagnosis of thyroid disease after applying GA as NN training, validation, and testing showed a significant difference at the 0.05 level and the better performance of the GA-MLP model compared with the PSO-MLP and BP-ANN models.
| Classifier | Training | Validation | Testing | Mean | ||||
|---|---|---|---|---|---|---|---|---|
| R% | Classification Accuracy, % | R% | Classification Accuracy, % | R% | Classification Accuracy, % | Total R% | Classification Accuracy, % | |
| BP-ANN | 71 | 70 | 67 | 67 | 68 | 68 | 70 | 68 |
| PSO-MLP | 90 | 89 | 85 | 97 | 84 | 97 | 88 | 85.5 |
| GA-MLP | 97 | 96 | 95 | 95 | 99 | 93 | 97 | 95 |
The Statistical Parameters of the Classifier Methods
The performance of the suggested method was contrasted with other techniques in the literature employing the current datasets. The results outline is demonstrated in Table 3. The examination demonstrated that the employed strategy had the second most astounding diagnosis accuracy, despite the fact that its accuracy was somewhat lower than those of some of the best previous methods. Due to the advantages of the mentioned method with respect to reported ones, it may be used as an alternative method in most of the laboratories.
| Method | Method Information | Classification Accuracy, % | Reference |
|---|---|---|---|
| GDA, WSVM | The feature extraction - feature reduction phase, classification phase, and GDA_WSVM test for thyroid disease phase determination, individually. | 91.86 | (28) |
| AIRS | Thyroid disease diagnosis with a novel hybrid machine learning technique comprising this grouping system. By hybridizing AIRS with a progressed fuzzy weighted preprocessing, a system was achieved to explain this diagnosis issue via classifying. | 81.00 | (29) |
| ARIS with fuzzy weighted preprocessing | 85.00 | ||
| MLNN with LMe | A comparative thyroid disease diagnosis was comprehended by the probabilistic, multilayer, learning vector quantization NNs. | 93.19 | (7) |
| Learning vector quantization | 90.05 | ||
| PNN | 94.62 | ||
| LDA | By LDA, an experimental study was performed to reach more reliable accuracy. | 99.62 | (30) |
| MLPNN | The research examined RBFNN and MLPNN for the structural classification of thyroid diseases. | 91.6 | (31) |
| RBFNN | 94.8 | ||
| K-nearest neighbor | Different characterization models were utilized to order T4U, TSH, and goiter. Many classification methods, such as K-nearest neighbor, Naive Bayes, and support vector machine, were applied. | 93.44 | (32) |
| Naive Bayes classifier | 22.56 | ||
| AIRS | Application of medical information gained based on AIRS. | 95.90 | (33) |
| SVM | The features, such as variance, mean, histogram feature, coefficient of local variation feature, homogeneity, and NMSID, were extorted and applied to train the classifiers such as SVM and ELM. | 84.78 | (34) |
| ELM | 93.56 | ||
| Radon-based approach | 90.9 | ||
| Fuzzy rule-based expert system | To diagnose thyroid disorders, a fuzzy rule-based classifier was designed. | 97 | (35) |
| The current study method (GA-MLP) | A comparison of PSO with GAs as training for the MLP method to diagnose thyroid functional disease. | 95 | This work |
| 85.5 | |||
| The current study method (PSO-MLP) |
The Diagnostic Accuracy of Approaches Available in the Literature and the Current Study for Thyroid Functional Disease
5.1. Conclusions
The current study results recommended that ANNs may likewise be utilized to develop a precise and successful model to predict thyroid functional disease. The results for the classification of the thyroid functional disease indicated that the system characterizes thyroid functional disease with the NN performance of 95% for GA-MLP and performance of 85.5% for PSO-MLP. The NN performance can further be upgraded by defining a higher goal error and training the ANN to progress the number of epochs to accomplish the predetermined objective.
The current study aimed at formulating diagnostic models of functional thyroid disease with suitable analytical characteristics by MLP ANNs. The results showed that GA is more successful than PSO in the diagnosis of functional thyroid disease and that the proposed GA-MLP can achieve very high diagnosis accuracy (95%). To streamline the diagnostic procedure in daily routine, prevent misdiagnosis, and reduce the cost of diagnosis in the early stages of the disease without using invasive procedures, the GA-MLP can be employed.
