1. Background
Major changes and challenges in the health sector such as the developments in the medical technologies have altered the status and position of hospitals and it clarifies the necessity of their careful and proper planning and management (1, 2). Patients may spend a lot of time getting the services they need due to poor hospital organization (3, 4). Diagnostic services are among the important hospital services, which are very expensive due to employing advanced facilities and technologies in which making and implementing the right managerial decisions is of high importance. The magnetic resonance imaging (MRI) department is a paraclinical and central one, which provides services to the inpatients and outpatients and helps physicians to diagnose the diseases (5, 6).
Waiting time can be measured as an indicator of hospital performance (7). Long waiting time indicates poor management, lack of coordination, and insufficient resources (8, 9), which impedes the provision of quality services in hospitals, wastes patients’ time, and reduces their satisfaction (10). Given that patients’ satisfaction with the waiting time plays an important role in improving the quality of services (11), it is necessary to review it as one of the most common problems in the hospitals (7).
To improve performance and reduce waiting time, the health system managers should be aware of the current state of business processes. The system analysis tools are used to understand the complexity of a system’s performance, determining the rate of access to pre-defined operational objectives, and how to improve them, among which the queuing theory is a tool to analyze systems that have queues and consist of clients, servers, and queues (12, 13). Queuing theory is a mathematical science-based approach to analyze waiting lines. The queuing models are used to achieve the equilibrium between the system capacity and costs of the delay in service delivery. Therefore, queuing theory is applied to minimize the costs through minimizing inefficiencies and delays in the system and increasing the patients’ satisfaction (14, 15). By a proper understanding of the queuing theory and variables related to the patients’ waiting time, the hospitals and health service managers can make the right and constructive decisions to improve and increase patients’ satisfaction (16).
Also, by simulating the results of queuing theory, different scenarios can be created to change the waiting time, system productivity, and the related costs. Simulation allows examining the effects of different solutions to improve the current situation and reduces the costs and risks of actual implementation of solutions (17, 18). The simulation with various scenarios can predict the results of making changes in the important elements of a system, including costs, waiting time, and staff, and help managers to make the right decisions to optimize the system performance (17, 18). The simulation results show a real picture of a system to the researchers through providing its dynamic analysis. This process improves the analyst’s understanding of the real relationships of the system more accurately (17, 19).
There are several studies conducted in the health sector using queuing theory and simulation such as those of O’Reilly et al. to optimize the DNA sequencing (20), Goldwasser et al. to estimate the public beds in intensive care units (ICUs) in Rio de Janeiro (21), Haghighinejad et al. to reduce waiting time in an emergency department in Iran (22), Antognini et al. to calculate the number of operating rooms needed to manage the non-elective surgical cases (23), Mathews and Long to improve the critical care patient flow and bed use (24), Mallor et al. to optimally control the ICU patient discharge (25), Komashie et al. to increase patients and staff’s satisfaction by providing an integrated model (16), Bettinelli et al. to plan emergency medical systems (26), Bahadori et al. to optimize the hospital pharmacy performance (14), Mohebbifar et al. to reduce the waiting time in the outpatient departments of health services and teaching hospitals (27), and White et al. to increase capacity in an emergency department (28). In the present study, since many patients were referred to the studied military hospital from different parts of the country, the overcrowding in all departments such as the paraclinical and imaging departments was a major problem and the large number of referrals exposed the patients to long waiting time. Therefore, the reorganization and optimization of the operating departments of this hospital was necessary.
2. Objectives
Given the high number of patients referred to the MRI department of this hospital and their waiting time, the current study aims at optimizing the performance of the mentioned MRI department using queuing theory and simulation to increase the productivity and patients’ satisfaction.
3. Methods
It was an applied and cross-sectional study conducted in 2015 in the MRI department of a military hospital affiliated to Baqiyatallah University of Medical Sciences, Iran, in in day (from 7 a.m. to 5 p.m.) and night (from 5 p.m. to 3 a.m.) shifts; the study population included all patients referred to the MRI department. The studied military hospital had about 45 departments and 700 available beds, which is one of the largest hospitals in Tehran and the main teaching hospital of the mentioned university with the accreditation degree of “excellent”.
In the present study, after receiving the required permission from the university authorities, the researchers referred to the studied hospital and provided the required explanations to the heads of hospital research unit, imaging department and the director of MRI department. To conduct the present study, the two following methods were used: interviews and observations. At the beginning of the study, several open interviews were conducted with the heads and managers of the studied MRI department to obtain preliminary data on this department and its processes and patients. To collect and determine the time of patients’ arrival and service delivery, some forms and checklists were prepared using the opinions of hospital managers and the MRI department heads and academic members.
To determine the sample size in this study due to the time distribution rules, the Poisson distribution (in this distribution the average is equal to variance) was used. Then, a sample of 264 patients was determined based on the service types by the following formula and the average number of patients referred to the MRI department in a month (from 5 July to 5 August 2015) by the service types, days, and work shifts, assuming α = 0.05 and d = 1/86.
n = [(Z1 – α / 2)2 × σ2 / d2]
The required samples were selected from each service based on the number of patients waited in the queues to receive the services in the morning and evening shifts using stratified sampling method proportional to the size and convenience sampling method; data were collected with the help of a stopwatch (timer) and forms of available samples in workstations. The content validity of the data collection form was approved by the study supervisor and 2 radiology experts working in the studied hospital.
The data were analyzed through the following steps, after documenting as follows:
First: The required data including the arrival rate in 2 work shifts (start-end), the time spent for patients’ admission (start-end), the time spent in the cashier station (start-end), the preparation time (start-end), the time of service delivery (start-end), the recovery time (start-end) and the time of giving required explanations to the patients, were gathered according to the service delivery processes and the queuing system of the MRI department and more to after gathered.
Second: All data and variables recorded in the data collection forms were transferred into the Excel 2013 by the service types and then analyzed.
Third: The results of the descriptive data processing and the calculation of queuing theory parameters in the MRI department were discussed with the simulation experts to model the queuing network of the MRI department and create various simulated scenarios based on the results of the queuing theory analyses to optimize the performance of the MRI department and reduce its patients’ waiting time. The collected data and the information required to model the MRI department were transferred into Arena 14.5. After interviewing the head of hospital imaging department, the director of MRI department and 2 radiology experts, and considering the hospital’s environmental conditions and the feasibility of scenarios in the medium term, 4 scenarios were created and studied based on making changes in the elements of queuing system such as the number and composition of employees and equipment according to the viewpoints of the interviewees and the study analysts.
Fourth: Based on the queuing theory analyses and the comparisons made among the outputs of proposed simulated models, the best model was suggested to optimize the performance of the studied MRI department.
It should be noted that in the current study, there was no direct communication with patients and there were interactions with the department management; the researchers explained the study aims and methods to the hospital research unit and assured them about the accuracy and reliability of the reported results; however, the present study was approved by the ethical committee of Baqiyatallah University of Medical Sciences (code number: CH/7018/998).
The limitation of the present study was that the diversity and multiplicity of radiology services and the need to transfer the delivery time of all services into the simulation scenarios made the study very complex. This complexity required more time, a lot of attention and patience in the two studied shifts, and enough time, attention, and patience were devoted to collect correct and accurate data and results.
4. Results
During the primary observations in the studied hospital MRI department, as well as according to the interview conducted with the director of MRI department, the required information were collected and presented in Tables 1 and 2.
Table 1. Personnel and Work Shifts in the Studied MRI Department
| Work Shifts | Hours | The Number of Receptionists | The Number of Preparation Process Employees | The Number of MRI Technologists | The Number of MRI Machines |
|---|---|---|---|---|---|
| Morning | 7 a.m. to 5 p.m. | 2 | 1 | 1 | 1 |
| Night | 5 p.m. to 3 a.m. | 1 | 1 | 1 | 1 |
Abbreviation: MRI, magnetic resonance imaging.
Table 2. The Daily Schedule of the Studied MRI Department
| Hours | Activities | Hours | Activities |
|---|---|---|---|
| From 7 a.m. to 8 a.m. | Preparing the machine and starting to work | From 5:30 p.m. to 7 p.m. | Knee coil - To prevent depreciation and damage, the machine is connected, and after providing the relevant services, it is disconnected and retracted. |
| From 8 a.m. to 10 a.m. | Performing MRIs in special cases that require an injection on specific organs, including hip, ankle, wrist, femur, elbow, and long bones | From 7 p.m. to 8 p.m. | Performing MRIs on the waist and knee - To prevent depreciation and damage, the machine is connected, and after providing the relevant services, it is disconnected and retracted. |
| From 10 a.m. to 2 p.m. | Performing MRIs in the patients admitted to the studied hospital departments and the outpatients (typical patients); lunch and praying | From 8 p.m. to 9 p.m. | Dinner and praying |
| From 2 p.m. to 4 p.m. | Typical cases, including spinal cord, brain, organs and limbs, hands and legs | From 9 p.m. to 12 p.m. | Performing general MRIs at night (head, whole body, pelvis) |
| From 4 p.m. to 4:30 p.m. | Performing MRIs on neck and shoulders (shoulders coil) - To prevent depreciation and damage, the machine is connected, and after providing the relevant services, it is disconnected and retracted. | From 12 p.m. to 3 a.m. | Performing general MRIs at midnight (head, whole body, pelvis) |
| From 4:30 p.m. to 5:30 p.m. | Performing MRIs on shoulders (shoulder coil) - To prevent depreciation and damage, the machine is connected, and after providing the relevant services, it is disconnected and retracted. | From 3 a.m. to 7 a.m. | Downtime |
Abbreviation: MRI, magnetic resonance imaging.
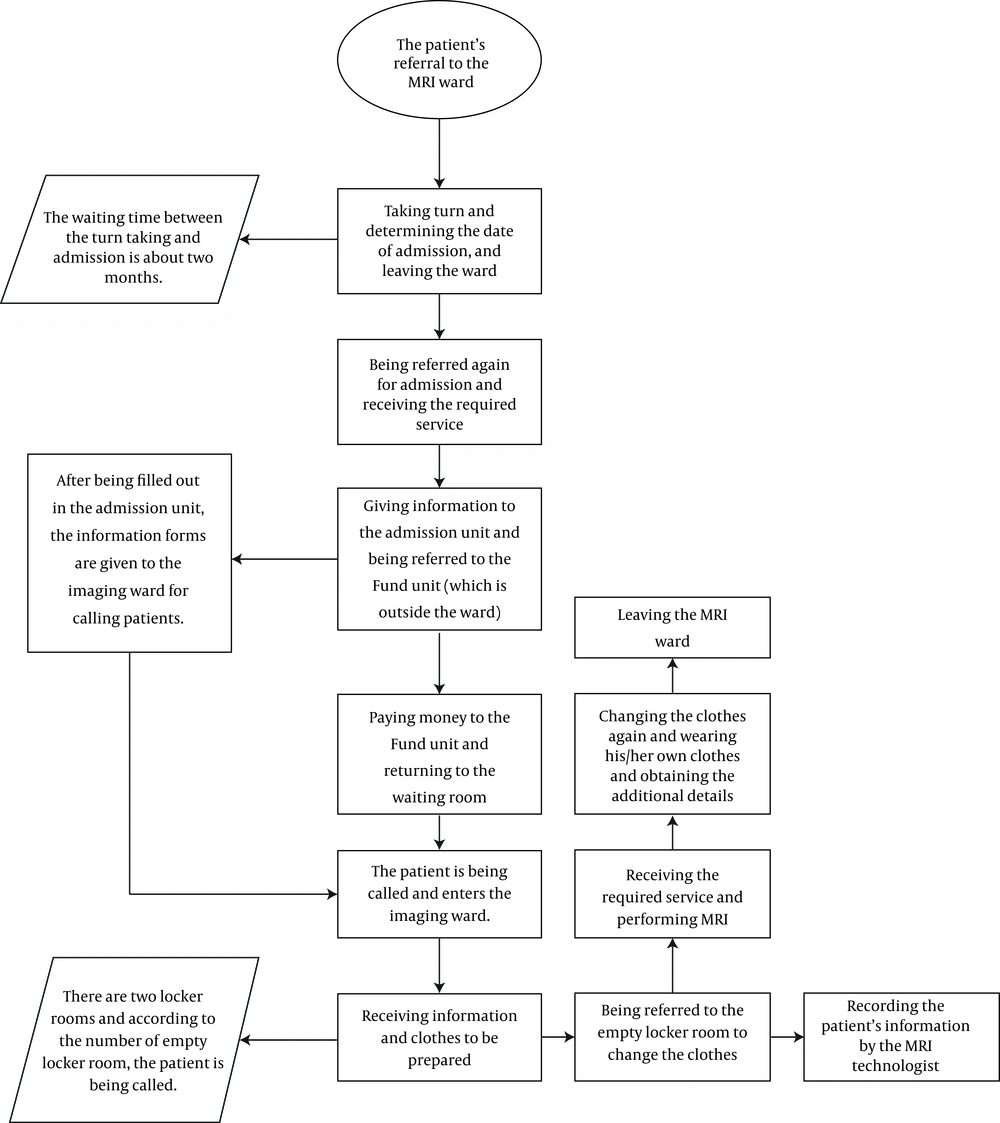
In the studied MRI department, the patients faced the following workstations from the time of entering the department for turn-taking until leaving it after receiving services:
1) Turn-taking and long waiting time (about 2 months) for admission
2) Admission
3) Paying to the cashier station
4) Being prepared to receive services (after being called, which was along with short waiting time)
5) Receiving Imaging service and leaving the department.
The more detailed description of the patient flow is presented in Figure 1.
Figure 1.
The Workflow and Patient Flow Chart in the Studied MRI Department
The flowchart was specific to the studied MRI department and was prepared by interviewing the MRI department managers, heads, and drawing the service delivery processes.
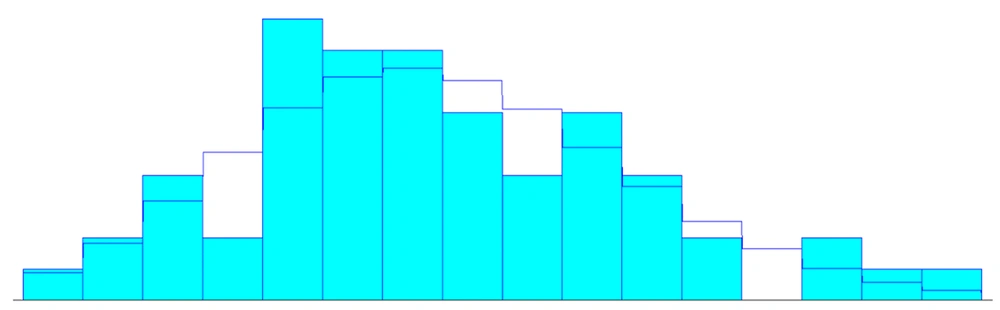
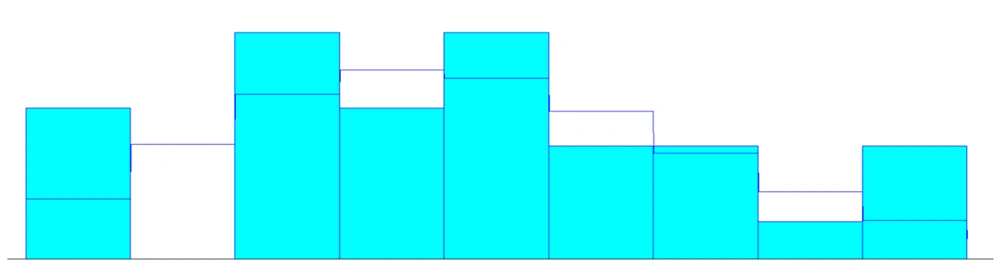
According to the determined sample size and selected samples, the patients’ arrival time in the studied MRI department for turn-taking and the service delivery time in various workstations until the time of leaving the MRI department after receiving the required services were recorded. The patients’ arrival in the MRI department and the time of service delivery in the two studied work shifts had Poisson and normal distribution, respectively (Figures 2 and 3).
Figure 2.
The Distribution of Patients’ Arrival Time in the Studied MRI Department for Turn-Taking in the Morning Shifts
Figure 3.
The Distribution of Patients’ Arrival Time in the Studied MRI Department for Turn-Taking in the Night Shifts
According to the recorded time, the queuing model of the studied hospital MRI department was as follows:
It should be noted that the studied MRI department provided, on average, 79 and 2360 services daily and monthly, respectively.
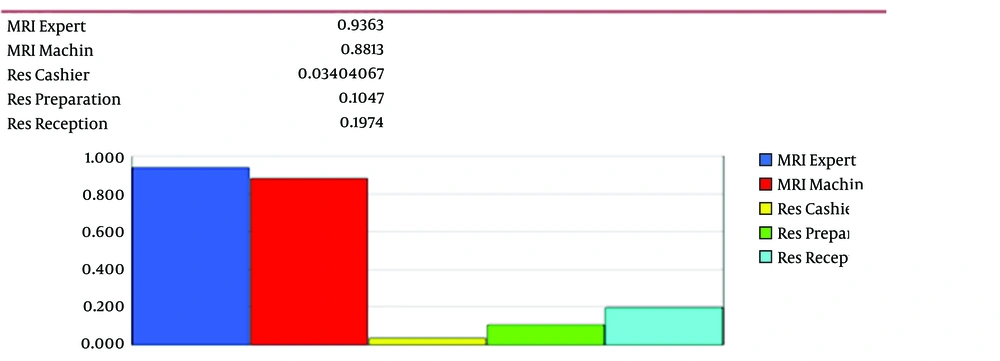
The above graph indicates that the MRI technologists were working at 93%, the MRI machine at 88%, the preparation process employees at 10%, and the receptionists at 19% of their capacities (Figure 4).
Figure 4.
The Productivity of the Studied MRI Department Employees and Machines
The results presented in Table 3 show that according to the available queuing model in the studied MRI department, on average, there were 5 patients in the queue of admission station, one patient in the queue of cashier station, 11 patients in the queue of preparation process and 2 patients in the queue of receiving the required services. The waiting time for turn-taking until admission was 56 days, for preparation process was 49 minutes, and for receiving the required services was 1 hour and 12 minutes.
Table 3. The Waiting Time in the Available Queuing Model in the Studied MRI Department
| Average | Minimum Value | Maximum Value | |
|---|---|---|---|
| The average number of people waiting in queue of | |||
| Admission station | 5.168 | 0.00 | 96.375 |
| Cashier station | 0.016 | 0.00 | 0.964 |
| Preparation process | 10.818 | 0.00 | 70.112 |
| MRI services | 2.190 | 0.00 | 3475.94 |
| Average waiting time in the year (minutes) for | |||
| Admission station | 80728.05 | 12.222 | 157019.14 |
| Preparation | 59.309 | 0.00 | 3607.59 |
| Wait for MRI services | 71.973 | 0.055 | 3604.45 |
According to the queuing model provided by Arena 14.5, various scenarios were created to reduce waiting time, increase employees’ productivity, and in general optimize the department performance as follows:
Model 1: Reducing 1 receptionist from the admission station in the morning shift
In this proposed model, the studied MRI department provided, on average, 78 and 2344 services daily and monthly, respectively. In this scenario, the MRI technologists were working at 93%, the MRI machine at 87%, the preparation process employees at 10%, and the receptionist at 29% of their capacities.
After reducing 1 receptionist from the admission station in the morning shift, the available queues in the studied MRI department will be as follows:
There will be 7 patients in the queue of admission station, 8 patients in the queue of preparation process, 2 patients in the queue of receiving the required services, and no patient in the queue of cashier station.
The waiting time will be as follows:
The waiting time for turn-taking until admission 56 days, for preparation process 54 minutes and the required services 54 minutes.
Model 2: Adding an hour to the working hours of the studied MRI department
In this proposed model, the studied MRI department provided, on average, 83 and 2499 services daily and monthly, respectively. In this scenario, the MRI technologists were working at 93%, the MRI machine at 88%, the preparation process employees at 10%, and the receptionist at 20% of their capacities.
After adding an hour to the working hours of the studied MRI department, the available queues in the studied MRI department will be as follows:
There will be 5 patients in the queue of admission station, 10 patients in the queue of preparation process, 2 patients in the queue of receiving the required services and no patient in the queue of cashier station.
The waiting time will be as follows:
The waiting time for turn-taking until admission 48 days, for preparation process 1 hour and for receiving the required services 1 hour and 7 minutes.
Model 3: Adding an hour to the working hours and reducing1receptionist from the admission station in the morning shift
In this proposed model, the studied MRI department provided, on average, 83 and 2482 services daily and monthly, respectively. In this scenario, the MRI technologists were working at 93%, the MRI machine at 88%, the preparation process employees at 10%, and the receptionist at 29% of their capacities.
After adding an hour to the working hours of the studied MRI department and reducing1receptionist from the admission station in the morning shift, the available queues in the studied MRI department will be as follows:
There will be 7 patients in the queue of admission unit, 8 patients in the queue of preparation process, 2 patients in the queue of receiving the required services, and no patient in the queue of cashier station.
The waiting time will be as follows:
The waiting time for turn-taking until admission 48 days, for preparation process 1 hour, and for receiving the required services 54 minutes.
Model 4: Adding an MRI machine and an MRI technologist
In this proposed model, the studied MRI department provided, on average, 104 and 3141 services daily and monthly, respectively. In this scenario, the MRI technologists were working at 61%, the MRI machine at 57%, the preparation process employees at 13%, and the receptionist at 26% of their capacities.
After adding an MRI machine and an MRI technologist, the available queues in the studied MRI department will be as follows:
There will be no patient in the queue of cashier station, 5 patients in the queue of admission station, 3 patients in the queue of preparation process, and 17 patients in the queue of receiving the required services.
The waiting time will be as follows:
The waiting time for receiving the required services will be 11 minutes, for preparation process 8 minutes and for turn-taking until admission without any waiting time.
The important points that can be observed in this model are the changes in the productivity of elements, and also the elimination of waiting time for turn-taking until admission, which is 56 days in the other models. It seems that this scenario made major changes compared with the three other scenarios and was more efficient than others in optimizing the department performance and reducing the waiting time.
5. Discussion
The results showed that the patients’ arrival time in the studied MRI department had the Poisson distribution which was consistent with those of Adeleke et al. (29), de Bruin et al. (30), and Kembe et al. (31). Given that the patients are referred to the studied MRI department from an unlimited population, the Poisson distribution for the patients’ arrival is logical and reasonable.
In the present study, the patients’ admission time, patients’ preparation time, service delivery time, and the time of leaving the studied MRI department had normal distribution, which were in line with the results of the study by Ajami et al. (32).
Also, the results showed that the highest average among the time of performing different activities in the studied MRI department was related to receiving the required services, which was reasonable due to the sensitivity of imaging and the need to ensure sufficient accuracy by the technologists when performing the MRI processes, and the conditions of the MRI machine. It should be noted that the time of delivering imaging services varies in different patients based on the location and the number of images.
Also, the time taken to perform MRIs with injecting an anesthetic was more than those of the outpatient and inpatient MRIs (types of services). For this type of imaging, some preparatory activities such as preparation of patients by physician and the patients’ family and administration of injections for anesthesia are needed. Also, patient’s handling and movement by the staff on the MRI machine increases the time of service delivery. The lowest average time were related to the recovery phase, giving required explanations to the patients, and leaving the MRI department. The results of Amina et al. (33) showed that the highest average time was related to the waiting time between requesting laboratory tests and receiving their results. The results of Pan et al. (18) showed that the highest and lowest average time were, respectively, related to the patients’ examinations by the residents studying in the 1st and 2nd years, and the time spent in the cashier station. Moreover, the results of Ameh et al. (34) showed that the highest and lowest average of waiting time were related to the orthopedic clinic and dermatology clinic, respectively.
In the present study, after calculating the average time of providing services in the different workstations, the available work flow and queues in the studied MRI department were determined.
Then, the results of analysis by reducing1receptionist, the productivity of receptionists, as well as the queue of patients’ admission increased and, on the other hand, the waiting time for receiving required services decreased. The reason can be that by reducing1receptionist, the activities of the remaining receptionists increases and by decreasing inputs (1 receptionist) and increasing outputs (the activities of other receptionists) and the ratio of outputs to inputs, the productivity of receptionists increases. By reducing1receptionist, the mean number of patients waiting in the queue increases, however, it is offset by increasing the productivity and, ultimately, the patients’ waiting time to receive the required services is reduced. Therefore, it can be concluded from these findings that the improvement of productivity and the greater use of internal and potential capacities of employees can reduce waiting time without any cost and even with downsizing. The results of Ajami et al. (35) showed that the patients’ waiting time before receiving services in the studied emergency department increased by decreasing1receptionist and providing services in the admission station only by1receptionist, which were inconsistent with those of the present study. This difference can be due to the differences in the nature of the departments studied in the two studies since the type of patients referred to the two departments, i e, emergency and MRI departments, are different and the waiting time in the two departments are also different. Moreover, this difference may be due to differences in the productivity of receptionists working in the admission station of these 2 departments.
Furthermore, the results of the current study showed that all existing queues and waiting time in the studied MRI department to receive the required services could be reduced by increasing the working hours. Based on the high referral to the studied MRI department, the major capacity of MRI machine was used; and given that all patients referred to this department were outpatients, increasing working hours can be more responsive and provide the necessary services to patients. Therefore, the referrals are distributed across the added hours and the waiting time and queues will be shorter. The result of Aeenparast et al. (17) indicating that the patients’ waiting time for examination can be reduced by increasing physicians’ working hours were in line with those of the present study.
The results of the current study showed that adding an MRI machine and an MRI technologist could decrease waiting time in all activities of the studied MRI department. As mentioned above, this scenario could make fundamental changes in the productivity of elements; it could also result in the elimination of waiting time for turn-taking until admission. Therefore, it seems that this scenario is more efficient than the other 3 scenarios to optimize the department performance and reduce the waiting time. In the current study, an MRI machine had to be added and necessarily a technologist to work with it. In this case, the technologist should be a full-time one. In other words, by adding an additional machine and according to the work shifts, either a technologist should be employed or the available technologists should work overtime. Therefore, for more detailed and accurate analysis, it is necessary to calculate the costs of human resources besides the costs of purchasing a machine. According to the results of the present study, the load of current referrals, previously taken by the existing MRI machine and MRI technologists, is distributed and the substantial reductions in the patients’ waiting time is achieved in the short term. It should be noted that over time and due to increased capacity for patients’ admissions (which is dependent on the service quality, advertising and promotions, and many other factors), the referrals and waiting time will increase again.
The results of the present study were similar to those of Zare Mehrjardi et al. (36), which showed that patients’ waiting time could significantly decrease by adding personnel. In the study by Duguay and Chetouane (37), the greatest decreases in the patients’ waiting time occurred by increasing a physician and a nurse and without adding any examination room. Ajami et al. (35) concluded that the patients’ waiting time could be decreased by adding an intern student to the studied specialized service. However, the main problem with adding resources is the large increases in the costs of using resources. In the 4th model of the current study, special attention should be paid to the cost-effectiveness considerations. As indicated, the patients’ waiting time for turn-taking until admission dramatically reduced by purchasing and using an additional MRI machine. Also, in the current situation, there was no possibility of physical space development in the studied MRI department and the MRI machine was also very expensive. These were some reasons to continue the current processes. However, it is necessary to conduct another study to compare the revenues produced by admitting new patients and reducing waiting time with the capital and current costs spent on purchasing an MRI machine and then making evidence-based decisions about purchasing an MRI machine and employing MRI technologists according to the break-even point.
According to the results of the proposed scenario, the mean waiting time could be significantly reduced by making small changes in the personnel (changes in the working hours and the number of personnel) and the number of machines (adding an MRI machine). Also, the results showed that, currently, the patients’ waiting time to receive the required services on average was 80728.05 minutes per year (56 days), and the department productivity on average was 52.5% indicating the high system capacity not used. There was dramatically reduced waiting time and increased required services in the 4th scenario. Therefore, using this scenario was appropriate and efficient to solve the current problems. However, final decisions on using this scenario require cost-benefit analyses.
