1. Background
Cancer has always been one of the issues facing human health all over the world to the extent that researchers and therapists have always sought to find better treatment methods to deal with this disease (1). Increasing the life expectancy of cancer patients has always been one of the main goals of treatment. The progress of science in the fields of pharmaceuticals and medical research, as well as finding better methods in the fields of surgery, radiotherapy, and chemotherapy, has led to an increase in the survival of cancer patients (2-4). In the progress of medical science in the field of cancer treatment, breast cancer (BC) is one of the pioneers, and early diagnosis and treatment methods have been able to significantly increase the survival of patients (5). Worldwide, BC is responsible for 15.0% of all cancer-related deaths in women, with an estimated 627 000 deaths in 2018 (6). In 2016, the 5-year survival rate of invasive BC patients was 77%, and their 15-year survival rate was 44% (7). In America, according to the availability of diagnostic facilities and organized data collection, 1 out of 8 women will be diagnosed with BC during their lifetime (8). According to the report presented by the e European Cancer Information System (ECIS) in 2018, BC was still reported as the most common cancer among women in Europe, with 29.2% of all cancers in women (9). In Iran, as a less developed country, BC accounts for 23% of all women's cancers (10). Along with the vast advances in medical sciences in the field of patient survival studies, the science of statistics was also developed. At first, methods such as Cox and Kaplan-Meier analysis, and later parametric and non-parametric methods, and then a variety of more complex survival data analysis methods were used to help researchers analyze these data (11). Although all of these methods are still applicable, due to the changing nature of survival data, especially in cancers with high recovery rates, better methods are needed for more accurate data analysis. As mentioned, the survival rate of BC patients has increased. In survival terminology, this data is called cured data (12). In the cured data, the survival rate is not decreasing, unlike its previous common state, but remains relatively flat from a certain time (13).
After identifying the cured data, newer statistical methods were proposed for more accurate analysis. The non-parametric and parametric mixture models were quickly advanced. Chen et al. (14) and others (15, 16) proposed Bayesian and frequentist extensions of these models. However, these models have limitations as they heavily rely on assumptions of parametric distributions or positive stable distributions, which may lead to less robust results when these assumptions are violated (17, 18). Additionally, the calculation of the hazard function in the suggested semi-parametric models poses challenges (16).
An alternative to mixture models, which is based on defective distribution, was proposed. These distributions do not normalize to one for certain parameter values and can fit survival-cured data without explicitly including the cure rate parameter (19). Initially, defective models were introduced, using well-known defective distributions such as Gompertz, inverse-Gaussian, and exponentiated-Weibull. Later, more flexible risk functions were achieved by developing defective models based on the Kumaraswamy and Marshall-Olkin families of defective distributions (19). Utilizing more accurate analysis methods can assist researchers in identifying more effective risk factors in survival rates and improving disease control planning (20, 21). Compared to mixture models, defective models require one less parameter to be estimated, resulting in fewer iterations and no failure in the maximum likelihood estimation (MLE) method. Additionally, precise estimation of presumed population proportions is not reflected in standard asymptotic inference (16). Another advantage of defective models is that the cure rate does not need to be known in advance; if the parameter space remains unchanged, it indicates the absence of a cure rate in the data (22, 23). Since Marchall Olkin and Kumaraswamy are families of distributions, various basic distributions like Gompertz, Weibull, and inverse-Gaussian can be easily incorporated into this family of distributions (20).
2. Objectives
The purpose of this study is to investigate the factors affecting the survival of BC patients, using cured models based on Kumaraswamy's defective distribution.
3. Methods
In the form of a retrospective longitudinal study, the information of 2 574 BC patients who visited Shohada Tajrish Hospital for treatment between September 2013 and September 2020 was collected. This information was recorded and collected at the Cancer Research Center affiliated with Shahid Beheshti University of Medical Sciences. All the patients who were selected for the study were those whose BC was confirmed by the pathologist and the pathology test. There were only 15 male patients among the patients who were excluded from the study. Patients whose information had many defects were excluded from the study (286 patients). Patients who died for reasons other than BC were also excluded from the study (159 patients). Finally, the data of 2 574 patients were included in the study for analysis. The dependent variable in this study was the time between diagnosis and death from BC among patients (in years). In terms of survival analysis terminology, death due to BC was considered the desired event. Also, only right censoring was investigated in this study for the patients who did not die during the study (83%). We tried to measure the clinicopathological and biological characteristics of BC that may be effective in the survival rate of patients using the cured model. Age at the diagnosis time, cancer stage, tumor size, tumor histologic grade, metastatic lymph node status, number of metastatic lymph nodes, lymphovascular invasion (LVI), HER2, KI67, P53, estrogen/progesterone receptor, chemotherapy treatment (CT), radiotherapy treatment (RT), hormone therapy (HT), and type of surgery as possible risk factors were included in the model.
In accordance with Rocha et al.'s article, we initially introduced the defective Kumaraswamy family of distribution and concluded that the Gompertz and inverse Gaussian distributions within this family provide the best fit for cured data, we utilized these two distributions in the Kumaraswamy family distributions (20). AIC, BIC, and CAIC are commonly used criteria to assess goodness-of-fit. Since AIC, BIC, and CAIC have distinct characteristics and assumptions for model selection, we employed all three criteria to determine the most suitable model for the data (24, 25). Additionally, we also applied a mixture model to compare further, ultimately selecting the model with the lowest ACI, BIC, and CAIC as the preferred model for interpreting coefficients. Consequently, we reported the risk factors influencing patient survival rate based on a significance level of 0.05.
4. Results
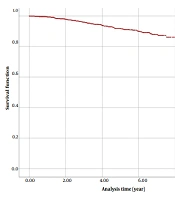
To check the nature of the data, the Kaplan-Meier survival chart was drawn. In Figure 1, it can be seen that the survival rate did not decrease after the 8th year and is a straight line, which shows the cure nature of the data.
Figure 1.
Kaplan-Meier estimate for the survival curve of breast cancer data
Given the large sample size (n = 2 574) of this study, both Bayesian and frequentist methods yield similar estimates. Furthermore, in studies with lengthy follow-up periods like this one (8 years), a substantial number of censored cases do not significantly impact estimates and can often be considered as cure rates. However, in studies with shorter follow-up times, distinguishing between censored cases and cured rates can lead to differences in estimates.
Three cured models, namely the mixture model, defective Kumaraswamy-Gompertz model, and defective Kumaraswamy-Inverse Gaussian model, were fitted to the data to analyze the impact of risk factors. The goodness-of-fit results are presented in Table 1. Maximum likelihood estimations (MLE) were obtained using numerical convergence and Newton-Raphson methods implemented in R software. The programs used for analysis can be provided upon request.
Table 1.AIC, BIC, and CAIC Values for the Fitted Distributions and for the Standard Mixture Model
| Model | AIC | BIC | CAIC | |
|---|---|---|---|---|
| Mixture | 0.73 | 596.71 | 590.36 | 593.61 |
| Defective Kumaraswamy Gompertz | 0.82 | 562.08 | 571.32 | 563.27 |
| Defective Kumaraswamy Inverse Gaussian | 0.78 | 583.62 | 587.45 | 584.71 |
Abbreviations: p ̂, estimate of cure fraction or cure rate; AIC, Akaike information criterion; BIC, Bayesian information criterion; CAIC, consistent AIC.
According to the results and the AIC, BIC, and CAIC criteria in Table 1, it is clear that the cured model using the defective Kumaraswamy family of distributions based on the Gompertz distribution had the best fit for the data. The estimated cure rate (
If we consider the Gomperts distribution for a > 0, b > 0, and t > 0 as follows:
And place it in the following formulas:
The probability density functions, survival, and hazard functions for the Kumaraswamy-Gompertz family for u > 0, b > 0, r > 0, and t > 0 are as follows:
If we set a < 0, we reach the family of defective Kumaraswamy-Gomperts distribution, in which the cure ratio is calculated as follows:
So p0 is the cure ratio for the defective Kumaraswamy-Gomperts distribution.
The covariates of interest can be obtained by parametrizing b as:
The hazard ratio (HR) for x1 versus x2 can also be obtained with:
Based on the Hessian matrix of the estimates (which can be calculated by the Newton-Raphson method), confidence intervals for the estimates can be calculated with the obtained standard deviation.
Based on the results of the defective Kumaraswamy Gompertz model for the cured data presented in Table 2, the variables of age (P-value = 0.046), tumor histologic grade (P = 0.038), tumor size (P = 0.041), HER2 (P = 0.001), KI67 (decrease) (P = 0.027), P53 (P = 0.029), and hormone therapy (P = 0.039) were significant. According to the results, it can be seen that the risk of death for people who are over 60 years old when the disease is diagnosed is 65% higher than for people who are under 40 years old, and the death hazard for HER2-positive patients is 43% higher than others. The risk of death for patients whose histological grade is poorly differentiated is 3.74 times that of patients whose grade is well-differentiated, for patients with T3 tumor size is 2.66 times that of patients whose tumor size is T1, and for patients with KI67 < 20% is 3.23 times that of others. The death hazard for patients with P53 negative is 2.107 times that of others, and for patients who did not receive hormone therapy, it is 2.83 times that of others.
Table 2.Clinicopathological and Biological Characteristics of BC Patients Using Cured Models Based on Defective Kumaraswamy Gompertz Distribution
| Variables and Categories | No. (%) | Hazard Ratio | 95% CI for HR | P-Value |
|---|---|---|---|---|
| Age at diagnosis (y) | ||||
| Under 40 | 642 (24.9) | Ref | - | - |
| 40 to 60 | 1436 (55.8) | 1.23 | (0.98 - 1.48) | 0.059 |
| Over 60 | 460 (19.9) | 1.65 | (1.48 - 2.05) | 0.046 |
| Unknown | 36 (1.4) | 1.12 | (0.91 - 1.33) | 0.063 |
| Tumor histologic grade | ||||
| 1 (well differentiated) | 228 (8.9) | Ref | - | - |
| 2 (moderately differentiated) | 1180 (45.8) | 1.740 | (1.12 - 1.93) | 0.085 |
| 3 (poorly differentiated) | 838 (32.6) | 3.746 | (2.96 - 4.02) | 0.038 |
| Unknown | 328 (12.7) | 1.205 | (1.04 - 1.38) | 0.079 |
| Stage | ||||
| I | 555 (21.5) | Ref | - | - |
| II | 939 (36.5) | 1.015 | (8.96 - 1.14) | 0.265 |
| III + (III and IV) | 936 (36.4) | 1.203 | (0.94 - 1.31) | 0.132 |
| Unknown | 143 (5.6) | 1.362 | (1.15 - 1.40) | 0.196 |
| Metastatic lymph node status | ||||
| Negative (-) | 1215 (47.2) | Ref | - | - |
| Positive (+) | 2474 (42.7) | 1.061 | (0.79 - 1.21) | 0.210 |
| Unknown | 259 (10.1) | 1.217 | (1.12 - 1.41) | 0.156 |
| Number of metastatic lymph nodes | ||||
| N0 (1 - 2) | 1779 (69.1) | Ref | - | - |
| N1 (3 - 5) | 251 (9.7) | 1.03 | (0.86 - 1.27) | 0.380 |
| N2+ (N2 and N3) (> 5) | 280 (10.8) | 1.16 | (0.74 - 1.18) | 0.231 |
| Unknown | 260 (10.1) | 1.08 | (0.84 - 1.38) | 0.426 |
| Tumor size | ||||
| T1 (0 - 2 cm) | 653 (25.4) | Ref | - | - |
| T2 (2 - 5 cm) | 1038 (40.3) | 0.68 | (0.49 - 0.73) | 0.090 |
| T3+ (T3 and T4) (> 5 cm) | 681 (26.5) | 2.66 | (2.01 - 2.97) | 0.041 |
| Unknown | 202 (7.8) | 1.31 | (1.12 - 1.49) | 0.067 |
| Estrogen receptor (ER) | ||||
| Negative (-) | 1841 (71.5) | Ref | - | - |
| Positive (+) | 219 (8.5) | 0.45 | (0.15 - 0.62) | 0.330 |
| Unknown | 514 (20) | 0.39 | (0.18 - 0.52) | 0.417 |
| Progesterone receptor (PR) | ||||
| Negative (-) | 1639 (63.7) | Ref | - | - |
| Positive (+) | 221 (8.6) | 1.32 | (1.04 - 1.38) | 0.374 |
| Unknown | 714 (27.7) | 0.98 | (1.04 - 1.38) | 0.291 |
| Lymphovascular invasion (LVI) | ||||
| Negative/probable = negative (-) | 781 (30.3) | Ref | - | - |
| Definite = positive (+) | 450 (17.5) | 1.047 | (1.01-1.098) | 0.221 |
| Unknown | 1343 (52.1) | 1.24 | (0.91 - 1.42) | 0.186 |
| HER2 | ||||
| Negative (-) | 1774 (69) | Ref | - | - |
| Positive (+) | 516 (20.0) | 1.43 | (1.28 - 1.72) | 0.001 |
| Unknown | 284 (11) | 1.02 | (0.92 - 1.31) | 0.074 |
| KI67 (decrease) | ||||
| > 20% | 1769 (68.7) | Ref | - | - |
| < 20% | 805 (31.2) | 3.23 | (2.97 - 3.48) | 0.027 |
| P53 | ||||
| Positive (+) | 1535 (59.6) | Ref | - | - |
| Negative (-) | 984 (38.2) | 2.107 | (1.98 - 2.53) | 0.029 |
| Unknown | 55 (2.1) | 1.048 | (0.94 - 1.37) | 0.083 |
| Chemotherapy treatment (CT) | ||||
| Yes | 1441 (56) | Ref | - | - |
| No | 372 (14.5) | 1.22 | (0.81 - 1.35) | 0.213 |
| Neo-adjuvant | 529 (20.6) | 1.16 | (0.91 - 1.39) | 0.274 |
| Unknown | 232 (9) | 1.34 | (0.76 - 1.43) | 0.209 |
| Radiotherapy treatment (RT) | ||||
| No | 58 (2.3) | Ref | - | - |
| Yes | 2072 (80.5) | 1.12 | (0.82 - 1.29) | 0.071 |
| Unknown | 444 (17.2) | 1.16 | (0.98 - 1.34) | 0.084 |
| Hormone therapy (HT) | ||||
| Yes | 1919 (74.6) | Ref | - | - |
| No | 439 (17.1) | 2.836 | (2.33 - 3.92) | 0.039 |
| Unknown | 216 (8.4) | 1.23 | (0.94 - 1.47) | 0.183 |
| Type of surgery | ||||
| BCS | 1865 (72.5) | Ref | - | - |
| MRM | 450 (17.5) | 1.12 | (0.81 - 1.19) | 0.113 |
| BCS/ MRM | 15 (0.6) | 1.09 | (0.95 - 1.23) | 0.093 |
| Subcutaneous mastectomy | 19 (0.7) | 1.23 | (0.83 - 1.31) | 0.184 |
| Unknown | 225 (8.7) | 1.17 | (0.63 - 1.26) | 0.157 |
5. Discussion
In this study and according to the selected model, age, tumor size, historical grade, HER2 and P53 status, KI67, and hormone therapy are the factors that affect the death hazard of patients. According to the HR size, tumor historical grade and KI67 status have a greater effect on the death hazard of BC patients. The value of the cured parameter in this study was estimated at 0.82, which indicates a high rate of recovery in patients. The results obtained in the current model were more accurate than other models, and the confidence intervals for the available parameters were smaller and more accurate than other survival models.
The use of defective distributions in the modeling of cured data does not have a long life, and despite the simplicity of interpretation and accuracy of these models, there are not many studies on the use of these models on cured data. Although methods such as machine learning and artificial intelligence have been used to identify the risk factors of cancer patients, it should be noted that not considering the cured feature in these models can reduce the accuracy (26, 27). On the other hand, it is much easier for non-statisticians to use existing programs of cured models. Along with the progress of medical sciences in various fields, progress in the field of medical data modeling is also of particular importance, and the use of more up-to-date and accurate models can definitely be a more suitable guide for the management of treatment and prevention of diseases.
The characteristics of survival data are that people can be followed in different time intervals, and the use of any of the cured models depends only on the existence of a smooth line in the Kaplan-Meier curve. Since the cured models also pay attention to the people who have recovered from the event, they can have more advantages than the former survival models and give more accurate and reliable estimates of the effect of significant risk factors to the researcher (28). The cured model introduced in this research, in addition to its simplicity and easy interpretation, is a suitable model compared to other cured models because of the fewer parameters it has. In addition, the most important advantage of this model is that it is not necessary to know the cure nature of data to use this model. If the data are not cured, contrary to the researcher's assumption, the model still fits well, and the closeness of the cured ratio to zero indicates to the researcher that the data used were not cured (20).
Mixture models, as the first models presented for the cured data, as well as two well-known distributions of cured models of defective distributions of Kumaraswamy, were fitted on the data. According to the GOF criteria, the Kumaraswamy defective model based on Gompertz distribution was selected as the best model, and its coefficients were presented to determine the risk factors affecting the survival rate of patients. In other studies that used Cox analyses and simpler survival models, different factors such as T stage, LVI, ER, and PR were introduced to the survival rate of patients (29, 30). A study conducted in 2000 analyzed the results of 40 clinical trials involving BC patients, who were followed up for an average of 10 to 20 years. The study revealed that neither age nor the type of radiotherapy had a notable impact on the patient’s survival rate (31). Another study that examined 194 clinical trials on BC patients showed that the use of newer drugs or the better use of existing drugs can be effective in improving the survival rate of patients. The use of tamoxifen in patients who received hormone therapy could significantly increase the survival rate. Considering that in the present study, hormone therapy was also effective on the survival rate, and considering that most of the hormone therapy drugs in this study were tamoxifen, it can be concluded that the model used is highly accurate and the results are in line with the results of 194 clinical trials (32). Although the results of this study are inconsistent with some studies (29, 33), the identification of factors consistent with those introduced in large clinical trials indicates the high accuracy of the model (31, 32). Some of the risk factors identified in this model have been identified separately in other studies (34), but the significance of the variables together and considering the cure nature of the data can give researchers more confidence in the prognosis of this disease and with higher accuracy. The use of the introduced model in prospective studies like clinical trials and on other data from different centers can probably be effective with high accuracy in identifying other factors affecting the survival rate of patients.
It is suggested that the survival of patients suffering from other cancers as well as other diseases, such as types of transplants in chronic kidney diseases, heart diseases, etc., should be investigated with this type of analysis to more accurately identify the factors affecting survival.
5.1. Conclusions
Due to not needing a special assumption, having a better fit to the data if there is a cured rate, easier to use and interpret than other existing cured models, fitting the cured rate if there is one, and not causing problems in the model when the data is not cured, it is recommended that the presented model be examined and paid attention to by researchers in future studies.
Another advantage of using the cured model is that, in addition to the proper estimation of the cured rate of recovered patients, parameters affecting the survival rate of other patients can be easily obtained.
Despite high recovery rates of BC patients in this study (82%) and according to the cured model patients aged over 60 years old, those with poorly differentiated histological grade tumors (grade not specified), tumor size T3, HER2 positive status, KI67 expression level below 20%, negative P53 status, and patients who have not received hormone therapy have poorer survival than others.
