Abstract
Background:
Breast cancer is the first cause of cancer-related deaths among women in Iran.Objectives:
The aim of the present study was to compare the traditional statistical analysis and data mining technique as the research methods for identifying the prognostic factors regarding the survival time of patients with breast cancer. Decision tree method is one of the predictive models that used in the medical field. The most used algorithms are classification and regression trees (CART), the quick, unbiased, efficient statistical tree (QUEST), Chi-square automatic interaction detector (CHAIDs) algorithm, and the C5.0 algorithm.Methods:
We used data for 438 patients, who were referred to cancer research center in Shahid Beheshti University of Medical Sciences. The patients were visited and treated during 1992 to 2012 and followed up until October 2014. The data were analyzed by regression logistic and decision tree method. Six measures for evaluation of predictive performance of different models were used.Results:
The C5.0 algorithm performed better than CHAID, QUEST, CART algorithms, and the logistic regression in predicting breast cancer survival. The multiple logistic regression results indicated that the factors of age at diagnosis, histologic grade, axillary lymph node status, and type of surgery were statistically significant with regard to the probability of death in patients with breast cancer. Moreover, based on C4.5 they reported that tumor size, age of menarche, hormonal therapy, axillary nodal status, and histological grade are the most prominent variables.Conclusions:
The more precise methods can identify the more accurate predictors. The decision tree method was able to predict the probability of death more accurately compared with the conventional logistic regression. Some improvements for classical classification tree such as boosting and bagging have been developed in order to obtain better predictive performance. We suggest that the modern classification tree method in the breast cancer context be the focus of future studies.Keywords
Decision Tree Survivability Breast Cancer Logistic Regression
1. Background
Breast cancer is the most diagnosed cancer among women worldwide (1). Overall, there are 1.67 million new cases and 0.52 million deaths all around the world (2). Breast cancer is the first cause of cancer-related deaths among women in Iran and is diagnosed in the range of 40 to 49 years (3, 4). Approximately, 12% of women will be diagnosed with breast cancer in their lifetime while 1.9% of them will be under the age of 35 at the diagnosis time (5). Survival of the patients with breast cancer is different due to their different clinical characteristics (6). However, rather than other cancers, the survivability is high, especially if the cancer is diagnosed early (5). The 5-year survival is ranged from 65% to 80% in all populations (2). In Iran, the increasing rate of mortality was higher for age between 15 to 49 years old compared to age > 50 (7). The prognostic factors of breast cancer can be grouped in 2 categories: chronological and biological (8). The first category is based on the amount of time present and the second category is based on the potential behavior of tumor. Lymph node status and tumor size are time-dependent factors, but histological grade is a biological factor (6). However, the effects of factors such as age at diagnosis, stage of cancer, the prescribed chemotherapy agent, lymph node status, tumor size, histological grade, hormonal factors, and family history are unclear and challenging topic still (9, 10).
The statistical methods help to identify the most important predictors among them regarding the outcome of patients’ survival time or recurrence of time. The more precise methods can identify the more accurate predictors, and consequently, the cancer is able to be managed effectively. The aim of the present study was to compare traditional statistical analysis and data mining technique as the research methods for identifying prognostic factors regarding patients with breast cancer’ survival time. The data mining technique was decision tree method by 4 algorithms and statistical method was the logistic regression. Decision tree method is one of the data mining tools that do not consider the distribution for outcome variable (11). Decision tree method partitions the similar patients into subgroups based on clinical features and survival time (12-14). There are several algorithms in decision tree method such as classification and regression tree (CART), Chi-squared automatic interaction detector (CHAID), Commercial version (C5.0), quick, unbiased, efficient statistical tree (QUEST) (11). By decision tree, we discover/explain several rules by patterns and relationship between the prognostic factor and survival rate outcome in the context of breast cancer.
2. Methods
2.1. Patients
The present retrospective study was performed on 500 patients with breast cancer, who were referred to cancer research center in Shahid Beheshti University of Medical Sciences, Tehran, Iran. The patients were visited and treated during 1992 to 2012 and followed up until October 2014 via phone calls to check if they are still alive or not. For these patients, 13 prognostic factors were recorded, including age at diagnosis, family history of cancer, abortion, breastfeeding, marital status, tumor size, estrogen and progesterone receptor status (positive for if more than 10% of tumor cells showed a nuclear staining) (15), type of surgery (modified radical mastectomy or breast conserving surgery), histologic and nuclear grading according to Scarf-Bloom-Richardson criteria (16), axillary Lymph node status (N0, N1, N2 and N3 category) (17), Lymphovascular invasionand, and stage of disease according to AJCC (18). We had complete data for 438 patients because of some incomplete information in their medical records. Eventually, dataset for 438 patients consisted of 13 predictor variables and 1 dependent variable. The dependent variable for decision tree method was considered as qualitative and is divided into survival and death. The protocol of the present study was confirmed by the ethical committee of Shahid Beheshti University of Medical Sciences. The data were analyzed by SPSS v20 and SPSS Modeler v14. The significant level was considered at 0.05.
2.2. Statistical Analysis
2.2.1. Univariate Analysis
Descriptive statistics of clinical, pathological, and biological characteristics of patients were shown in Table 1. We assessed the differences of these characteristics between patients, who had survived and had not survived, by Univariate analysis. For all the discreet, variables comparison was made between 2 groups by the Chi-square test and Mann-Whitney test.
Comparisons of the Clinical, Pathological, and Biological Characteristics of the Patients by Survived or Not: Univariate and Multiple Analysis
| Variables | Survived (N = 363) | Deceased (N = 75) | Total (N = 438) | Univariat Analysis | Multiple Analysis | |
|---|---|---|---|---|---|---|
| P Value | OR | P Value | ||||
| Surgery | ||||||
| BCS | 253 (92.3) | 21 (7.7) | 272 (100) | < 0.001 | Reference | |
| MRM | 110 (67.1) | 54 (32.9) | 164 (100) | 3.7 | < 0.001 | |
| Stage | ||||||
| I | 92 (95.8) | 4 (4.2) | 96 (100) | < 0.001 | Reference | |
| II | 175 (90.7) | 18 (9.3) | 193 (100) | 0.66 | 0.5 | |
| III | 91 (67.4) | 44 (32.6) | 135 (100) | 0.45 | 0.3 | |
| IV | 5 (35.7) | 9 (64.3) | 14 (100) | 1.12 | 0.9 | |
| Grade | ||||||
| I | 46 (97.9) | 1 (2.1) | 47 (100) | < 0.001 | Reference | |
| II | 211 (89.8) | 24 (10.2) | 235 (100) | 3.7 | 0.2 | |
| III | 106 (67.9) | 50 (32.1) | 156 (100) | 11.8 | 0.03 | |
| Lymphovascular invasion (LVI) | ||||||
| Negative | 241 (90.6) | 25 (9.4) | 266 (100) | < 0.001 | Reference | |
| Positive | 122 (70.9) | 50 (29.1) | 172(100) | 1.1 | 0.7 | |
| Estrogen receptor | ||||||
| Negative | 95 (75.4) | 31 (24.6) | 126 (100) | 0.008 | Reference | |
| Positive | 268 (85.9) | 44 (14.1) | 312 (100) | 0.5 | 0.2 | |
| Progesterone receptor | ||||||
| Negative | 114 (76) | 36 (24) | 150 (100) | 0.006 | Reference | |
| Positive | 249 (86.5) | 39 (13.5) | 288 (100) | 1.3 | 0.5 | |
| Tumor Size | ||||||
| < 2 | 103 (92.8) | 8 (7.2) | 111 (100) | < 0.001 | Reference | |
| 2 - 5 | 208 (86) | 34 (14) | 242 (100) | 1.2 | 0.6 | |
| ≥ 5 | 52 (61.2) | 33 (38.8) | 85 (100) | 1.8 | 0.3 | |
| Lymph node status | ||||||
| N0 | 188 (94.9) | 10 (5.1) | 198 (100) | < 0.001 | Reference | |
| N1 | 105 (86.8) | 16 (13.2) | 121 (100) | 2.4 | 0.08 | |
| N3 | 27 (69.2) | 12 (30.8) | 39 (100) | 8.3 | 0.002 | |
| N4 | 43 (53.8) | 37 (46.2) | 80 (100) | 9.2 | 0.001 | |
| Abortion | ||||||
| Yes | 126 (82.4) | 27 (17.6) | 153 (100) | 0.8 | ||
| No | 237 (83.2) | 48 (16.8) | 285 (100) | - | - | |
| Family history of cancer | ||||||
| Yes | 106 (85.5) | 18 (14.5) | 124 9100) | 0.3 | ||
| No | 257 (81.8) | 57 (18.2) | 314 (100) | - | - | |
| Marital status | ||||||
| Single | 22 (91.7) | 2 (8.3) | 24 (100) | 0.4 | ||
| Married | 341 (82.4) | 73 (17.6) | 414 (100) | - | - | |
| Breastfeeding | ||||||
| Yes | 313 (82.2) | 68 (17.8) | 381 (100) | 0.3 | ||
| No | 50 (87.7) | 7 (12.3) | 57 (100) | - | - | |
| Age at diagnosis | ||||||
| < 40 | 63 (71.6) | 25 (28.4) | 88 (100) | 0.005 | Reference | |
| 40 - 70 | 289 (86) | 47 (14) | 336 (100) | 0.5 | 0.04 | |
| ≥ 70 | 11(78.6) | 3 (21.4) | 14 (100) | 1.08 | 0.9 | |
2.2.2. Decision Tree Algorithms
Decision tree method is one of the predictive models used in the medical field. It is a nonparametric and powerful method that recursively split observations into branches to construct a tree (19). The tree structure consisted of nodes (or leaves) and branches. Each node represents a value of the outcome variable given the values of the input variables represented by the path from the root to the node. There are several mathematical algorithms in decision tree method for identifying a variable and its best corresponding threshold for splitting observations into 2 or more homogeneous branches. The most used algorithms are classification and regression trees (CART) based on Gini index, the quick, unbiased, efficient statistical tree (QUEST) based on Chi-square or ANOVA test, Chi-square automatic interaction detector (CHAIDs) algorithm based on Chi-square test, and the C5.0 algorithm based on the information gain index. We used the default settings in the SPSS Modeler software package for building the tree in CART, CHAID, QUEST, and C5.0 algorithms. Maximum tree depth was 5, with minimum cases in parent node of 100.
To assess the predictive performance of each algorithm, a 10-fold cross validation method was used. In this method, the total of the dataset was divided into 10 subsets. Each subset was used to test the predictive performance of the model that was generated from the remaining 9 subsets as the model derivation sample. This leads to 10 independent performance estimates; then, validation results were averaged over 10 subsets to produce a single estimation (20).
2.2.3. Logistic Regression
Logistic regression is a generalization of liner regression for dichotomous outcome. It is one of the accepted methods that build a model between the probability of the binary event and predictor variables by logistic function (21). The output of the logistic regression is the probability of the event so it will always be some number between 0 and 1. Thus, we can never get a risk estimate either above 1 or below 0 in the logistic regression. The probability greater than 0.5 it means patients are designed to class addressed as “1”. This probability gives the risk of getting a disease for an individual in epidemiologic term. In the present study, we used logistic regression for prediction of the outcome of survived and deceased in patients with breast cancer, and variables that were statistically significant in univariate analysis were entered in the model by forward stepwise method (22).
3. Results
3.1. Patients Characteristics
The clinical, pathological, and biological characteristics of 438 breast cancer women were presented in Table 1. The mean age at the time of diagnosis was 48.37 ± 10.92 with the range of 22 to 40 years. The mean duration of follow-up was 52.3 with the range of 3 to 253 months. During the study up to October 2014, a total of 75 (17.12%) deaths caused by breast cancer were recorded. Using the life-table method, the 1-year overall survival rate was 98% (95% CI: 97% - 99%). The univariat analysis showed that age at diagnosis (P = 0.005), type of surgery (P < 0.001) lymph node status (P < 0.001), tumor size (P < 0.001), stage (P < 0.001), histologic grade (P < 0.001), estrogen receptor (P = 0.008), progesterone receptor (P = 0.006), and lymphovascular invasion (P < 0.001) were statistically significant prognostic factors for survival outcome. Abortion, marital status, breastfeeding, and family history factors were not statistically significant (Table 1). Variables that were significant in univariate analysis were entered into a multiple logistic regression model. Logistic regression results indicated that among these variables, type of surgery, histologic grade, and lymph node status were statistically significant.
3.2. Evaluation of Predictive Performance of Different Models
In the present study, 6 measures for evaluation of predictive performance of different models were used: accuracy, sensitivity, specificity, positive predictive value, negative predictive value, and area under the receiver operating characteristic curve (AUC). Table 2 showed these measures for cross-validation set of CART, CHAID, QUEST, C5.0 algorithms, and logistic regression models. The accuracy value ranged from 82.9% to 86.4% that the minimum accuracy was for QUEST and the maximum accuracy was for C5.0 algorithm. Also, the sensitivity, specificity, positive predictive value, negative predictive value, and AUC values ranged from 0 to 67.4%, 88.4% to 100%, 38.7% to 62.7%, 82.8% to 96.2% and 0.78% to 0.86%, respectively. For sensitivity and negative predictive values, C5.0 algorithm was higher than others, while for specificity and positive predictive values, QUEST algorithm and logistic regression were higher than the others, respectively. The logistic regression had the higher AUC value, CART ranked second, CHAID ranked third, followed by QUEST and C5.0. Overall, as shown in Table 2, C5.0 performed better than CHAID, QUEST, CART algorithms, and the logistic regression in predicting breast cancer survival.
Comparison of the Models Performance
| Model | Accuracy | Sensitivity | Specificity | Positive Predictive Value | Negative Predictive Value | AUC |
|---|---|---|---|---|---|---|
| Decision tree (CART) | 85.2 | 50.6 | 92.2 | 57.5 | 90.05 | 0.83 |
| Decision tree (CHAID) | 85.2 | 50.6 | 92.2 | 57.5 | 90.05 | 0.81 |
| Decision tree (QUEST) | 82.9 | 0 | 100 | - | 82.8 | 0.80 |
| Decision tree (C5.0) | 86.4 | 67.4 | 88.4 | 38.7 | 96.2 | 0.78 |
| Logistic regression | 85.8 | 42.6 | 94.7 | 62.7 | 88.8 | 0.86 |
3.3. Decision Rules of CART, CHAID, QUEST and C5.0 in Predicting Breast Cancer Survival
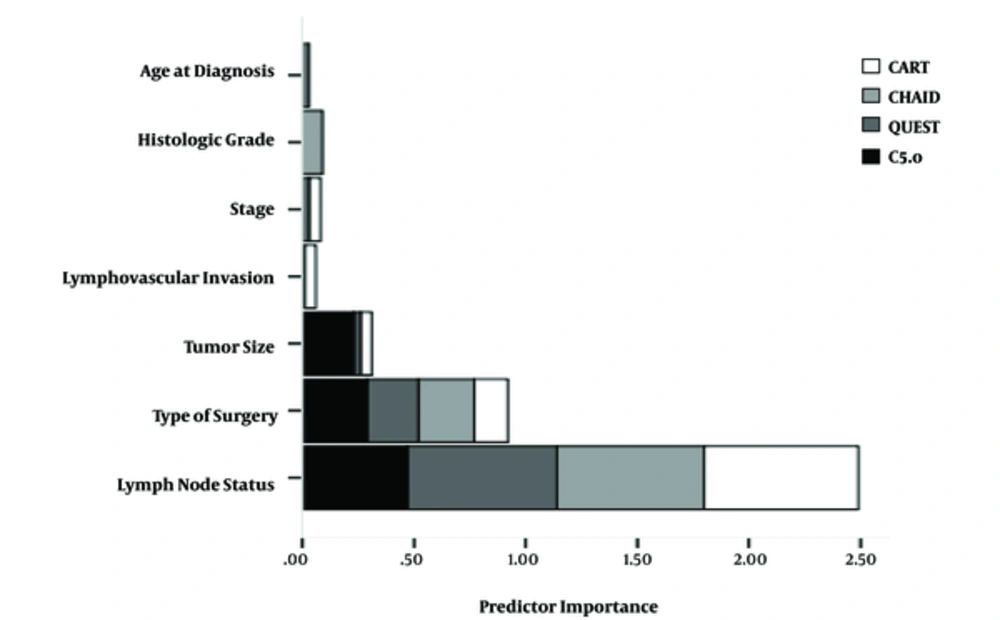
Decision rules provide information about risk factors that play important roles in explaining the survival. Rules were generated from the path of the root node to terminal nodes. Due to the prevalence of death in the total sample in this study, population was 17.12%; those terminal nodes consisting of more than 17.12% death are considered as higher risk groups and have been bolded in Table 3. As shown in Table 3, of the potential 9 variables from the candidate list (Table 1) 2, 3, 3, and 4 variables remained in tree structure based on CART, CHAID, QUEST, and C5.0 algorithms, respectively. Lymph node status was identified the most important prognosis factor for death by CART, QUEST, and CHAID algorithms, while the type of surgery created the first-level split in C5.0. shows shows the predictor importance by indicating the relative importance of each predictor in making the prediction of the model. Since values are relative, the sum of values for all predictors is 1.0 in each algorithm.
Terminal Nodes of the Different Models
| Model | Terminal Nodes | % Death |
|---|---|---|
| Decision tree (CART) | ||
| Node 1 | Lymph node status (N0 or N1) | 8.2 |
| Node 2 | Lymph node status (N3 or N4 ) + surgery (BCS) | 20.8 |
| Node 3 | Lymph node status (N3 or N4 ) + surgery (MRM) | 57.6 |
| Decision tree (CHAID) | ||
| Node 1 | Lymph node status (N0) + Grade (≤ 2) | 0.7 |
| Node 2 | Lymph node status (N0) + Grade (> 2) | 16.07 |
| Node 3 | Lymph node status (N1) + surgery (BCS) | 4.11 |
| Node 4 | Lymph node status (N1) + surgery (MRM) | 27.08 |
| Node 5 | Lymph node status (N3 or N4 ) + surgery (BCS) | 20.76 |
| Node 6 | Lymph node status (N3 or N4 ) + surgery (MRM) | 57.58 |
| Decision tree (QUEST) | ||
| Node 1 | Lymph node status (N3) | 46.2 |
| Node 2 | Lymph node status (N0 or N1 or N2) + surgery (MRM) | 22.8 |
| Node 3 | Lymph node status (N0 or N1 or N2) + surgery (BCS) + Grade (> 2) | 13 |
| Node 4 | Lymph node status (N0 or N1 or N2) + surgery (BCS) + Grade (≤ 2) | 1.7 |
| Decision tree (C5.0) | ||
| Node 1 | surgery (BCS) | 7.6 |
| Node 2 | surgery (MRM) + Lymph node status (N0) | 6 |
| Node 3 | surgery (MRM) + Lymph node status (N2) | 62.5 |
| Node 4 | surgery (MRM) + Lymph node status (N3) + Tumor size (≤ 5) | 39.1 |
| Node 5 | surgery (MRM) + Lymph node status (N3) + Tumor size (> 5) | 70.3 |
| Node 6 | surgery (MRM) + Lymph node status (N1) + LVI (positive) | 16 |
| Node 7 | surgery (MRM) + Lymph node status (N1) + LVI (negative) + Tumor size (≤ 5) | 18.7 |
| Node 8 | surgery (MRM) + Lymph node status (N1) + LVI (negative) + Tumor size (> 5) | 85.7 |
Variables Importance by the Different Models
In the CART algorithm, 2 initial branches were lymph node status: N0 or N1versus N3 or N4. Those who reported the lymph node status: N0 or N1comprised the lowest risk group others than patients (8.2% death). For those who reported the Lymph node status:N3 or N4, type of surgery was the second important predicting factor such that those who had modified radical mastectomy were classified as higher risk group (57.6% death) compared with those who had breast conserving surgery (20.8% death).
According to the CHAID classification tree, after the first-level split produced by the lymph node status variable the grad and surgery variables also entered the model. In this model, the lowest risk group comprised those who reported the lymph node status: N0 and Grade ≤ 2 (0.7% death). Also, those who reported the lymph node status: N3 or N4 and modified radical mastectomy were classified as the highest risk group (57.58% death).
Based on QUEST algorithm, the classification tree built the optimal split by 3 prognosis factors: lymph node status, type of surgery, and grad. The first terminal node was the highest risk group and consisted of individuals who reported the lymph node status: N3 (46.2% death). According to the first data, split subjects who reported the lymph node status: N1 or N2 or N3 went on to further subdivisions based on type of surgery. Terminal node 2 was the second high risk group (22.8% death) and followed by terminal node 3. Terminal node 4 comprised those who reported the lymph node status: N0 or N1 or N2 and breast conserving surgery and grade ≤ 2 were classified as the lowest risk group (1.7% death).
The final classification tree, based on C5.0 algorithm, generated 8 terminal nodes, and 4 variables were used to construct the tree. The first variable, which best divided the sample, was type of surgery. Overall, node 1, node 2, and node 5 were identified by C5.0 as the low risk groups. Low risk groups according to this tree consisted of subjects, who experienced breast conserving surgery (7.6% death), subjects who experienced modified radical mastectomy, and lymph node status: N0 (6% death) and subjects who experienced modified radical mastectomy and lymph node status: N1 and positive LVI (16% death). Also, the highest risk group based on this tree consisted of those who experienced modified radical mastectomy, lymph node status: N1, negative LVI and Tumor size > 5 (85.7% death).
4. Discussion
The objective of decision tree method is to classify subjects into homogenous categories based on their observed characteristics. Traditional statistical methods often cannot determine as well interactions between clinical variables on outcome of survival to translating this information into appropriate management (23), while decision tree method can explore the interactions between variables to find homogenous subgroups of patients with different prognosis factors regarding outcome of survival (24). Thus, the decision tree method is accompanied by results that are applicability in real settings in the medical field. In the present study, we compared the performance of decision tree method based on 4 algorithms and regression method by considering the outcome of survived and deceased.
The logistic regression had not been greater predictive ability compared with decision tree method based on C5.0 algorithm. In breast cancer context, several studies examined the predictive ability of data-mining methods for predicting the probability of death. They found that these methods resulted in improved predictive accuracy compared with the conventional regression methods (5, 10, 25). In summary, we found that among patients with breast cancer, the decision tree method based on C5.0 algorithm was able to predict the probability of death more accurately compared with the conventional logistic regression and other algorithms of decision tree method.
Our study showed association between clinical and pathologic factors and survival in patients with breast cancer. In multiple logistic regression factors of age at diagnosis, histologic grade, axillary lymph node status, and type of surgery were statistically significant with the probability of death in patients with breast cancer as observed in other studies (25-27). Histological grade (OR = 11.8; P = 0.03) and the involvement of axillary nodes by tumor (OR = 9.2; P = 0.001) that are biological factors were highly correlated with long-term survival. According to the Fisher’s study, the presence or absence of involved axillary lymph nodes is the single best predictor of survival from breast cancer (28). Histological grade is established on a combination of scores for mitotic rate, nuclear grade, and architectural morphological appearance (29). Several studies have shown the importance of histologic grade in predicting breast cancer recurrence (30, 31). Also, these 2 factors were reported in several studies as the important prognosis factors (27, 32). The odds of survival decreased with higher age at the diagnosis and type of modified radical mastectomy rather than breast conserving surgery. Patients’ age for predicting response to chemotherapy and hormone therapy is significant but, recent studies have proposed that a young age of less than 35 years is associated with an excess of high grade tumors and a poorer survival rate (33). According to the Fourquet’s study, the local control of the disease increases linearity with age (34).
A more helpful method of assessing risk of relapse is to combine several factors, to identify groups of women with different prognoses (8). On the basis of C5.0 method, the type of surgery, axillary lymph node status, Lymphovascular invasionand, and tumor size were the most important variables. According to the CART method, Sauerbrei et al. reported that tumor size and grade are the most important factors for the prognosis of recurrence-free survival in patients with breast cancer (35). Ture et al. found C4.5 algorithm, performing better than other algorithms in the decision tree method for recurrence-free and disease-free survival of patients with breast cancer (6, 25). Based on C4.5, they reported that tumor size, age of menarche, hormonal therapy, axillary nodal status, quadrant of tumor, and histological grade were the most prominent variables. Also, they showed for recurrence-free survival base on this algorithm, the subgroup of patients, who had tumor size < 4.4 cm and age of menarche ≥ years-old, are classified as the lowest risk group (7.3% recurrence) and subgroup of patients, who had tumor size ≥ 4.4 cm and receiving no hormonal therapy, are classified as the highest risk group (79% recurrence). The characteristics of the highest and the lowest risk group this study were different from the results of this study due to different variables used in 2 studies.
In our study, there are some limitations. Some clinical and pathological characteristics of patients were missing and that this information was from a single institution. Moreover, large sample size is a desirable property for data-mining methods, but our dataset was not very big. In the decision tree method, some improvements for classical classification tree such as boosting and bagging have been developed (14). These improvements contain aggregating classifications across a set of classification trees to obtain better predictive performance. In the present study, we used conventional decision tree method to classify patients with breast cancer by considering the outcome of survived and deceased. We suggest that the modern classification tree method in the breast cancer context be the focus of future studies.
Acknowledgements
References
-
1.
Garcia-Laencina PJ, Abreu PH, Abreu MH, Afonoso N. Missing data imputation on the 5-year survival prediction of breast cancer patients with unknown discrete values. Comput Biol Med. 2015;59:125-33. [PubMed ID: 25725446]. https://doi.org/10.1016/j.compbiomed.2015.02.006.
-
2.
Baghestani AR, Moghaddam SS, Majd HA, Akbari ME, Nafissi N, Gohari K. Survival Analysis of Patients with Breast Cancer using Weibull Parametric Model. Asian Pac J Cancer Prev. 2015;16(18):8567-71. [PubMed ID: 26745118]. https://doi.org/10.7314/APJCP.2015.16.18.8567.
-
3.
Haghshenas MR, Mousavi T, Moosazadeh M, Afshari M. Human papillomavirus and breast cancer in Iran: a meta- analysis. Iran J Basic Med Sci. 2016;19(3):231-7. [PubMed ID: 27114791].
-
4.
Momenyan S, Sadeghifar M, Sarvi F, Khodadost M, Mosavi-Jarrahi A, Ghaffari ME, et al. Relationship between Urbanization and Cancer Incidence in Iran Using Quantile Regression. Asian Pac J Cancer Prev. 2016;17(S3):113-7. [PubMed ID: 27165247]. https://doi.org/10.7314/APJCP.2016.17.S3.113.
-
5.
Chao CM, Yu YW, Cheng BW, Kuo YL. Construction the model on the breast cancer survival analysis use support vector machine, logistic regression and decision tree. J Med Syst. 2014;38(10):106. [PubMed ID: 25119239]. https://doi.org/10.1007/s10916-014-0106-1.
-
6.
Ture M, Tokatli F, Kurt I. Using Kaplan–Meier analysis together with decision tree methods (C&RT, CHAID, QUEST, C4.5 and ID3) in determining recurrence-free survival of breast cancer patients. Expert Syst Appl. 2009;36(2):2017-26. https://doi.org/10.1016/j.eswa.2007.12.002.
-
7.
Taghavi A, Fazeli Z, Vahedi M, Baghestani AR, Pourhoseingholi A, Barzegar F, et al. Increased trend of breast cancer mortality in Iran. Asian Pac J Cancer Prev. 2012;13(1):367-70. [PubMed ID: 22502702]. https://doi.org/10.7314/APJCP.2012.13.1.367.
-
8.
Bundred NJ. Prognostic and predictive factors in breast cancer. Cancer Treat Rev. 2001;27(3):137-42. [PubMed ID: 11417963]. https://doi.org/10.1053/ctrv.2000.0207.
-
9.
Davoodi SH, Malek-Shahabi T, Malekshahi-Moghadam A, Shahbazi R, Esmaeili S. Obesity as an important risk factor for certain types of cancer. Iran J Cancer Prev. 2013;6(4):186-94. [PubMed ID: 25250133].
-
10.
Delen D, Walker G, Kadam A. Predicting breast cancer survivability: a comparison of three data mining methods. Artif Intell Med. 2005;34(2):113-27. [PubMed ID: 15894176]. https://doi.org/10.1016/j.artmed.2004.07.002.
-
11.
Han J, Pei J, Kamber M. Data mining: concepts and techniques. Elsevier; 2011.
-
12.
Kourou K, Exarchos TP, Exarchos KP, Karamouzis MV, Fotiadis DI. Machine learning applications in cancer prognosis and prediction. Comput Struct Biotechnol J. 2015;13:8-17. [PubMed ID: 25750696]. https://doi.org/10.1016/j.csbj.2014.11.005.
-
13.
Austin PC. A comparison of regression trees, logistic regression, generalized additive models, and multivariate adaptive regression splines for predicting AMI mortality. Stat Med. 2007;26(15):2937-57. [PubMed ID: 17186501]. https://doi.org/10.1002/sim.2770.
-
14.
Austin PC, Tu JV, Ho JE, Levy D, Lee DS. Using methods from the data-mining and machine-learning literature for disease classification and prediction: a case study examining classification of heart failure subtypes. J Clin Epidemiol. 2013;66(4):398-407. [PubMed ID: 23384592]. https://doi.org/10.1016/j.jclinepi.2012.11.008.
-
15.
Zhang D, Salto-Tellez M, Putti TC, Do E, Koay ES. Reliability of tissue microarrays in detecting protein expression and gene amplification in breast cancer. Mod Pathol. 2003;16(1):79-84. [PubMed ID: 12527717]. https://doi.org/10.1097/01.MP.0000047307.96344.93.
-
16.
Bloom HJ, Richardson WW. Histological grading and prognosis in breast cancer; a study of 1409 cases of which 359 have been followed for 15 years. Br J Cancer. 1957;11(3):359-77. [PubMed ID: 13499785]. https://doi.org/10.1038/bjc.1957.43.
-
17.
Singletary SE, Allred C, Ashley P, Bassett LW, Berry D, Bland KI, et al. Revision of the American Joint Committee on Cancer staging system for breast cancer. J Clin Oncol. 2002;20(17):3628-36. [PubMed ID: 12202663]. https://doi.org/10.1200/JCO.2002.02.026.
-
18.
Fleming I, Cooper J, Henson D, Hutter R, Kennedy B, Murphy G. American joint committee on cancer. Cancer manual staging. 5 ed. 1997.
-
19.
Majidi Zolbanin H, Delen D, Hassan Zadeh A. Predicting overall survivability in comorbidity of cancers: A data mining approach. Decis Support Syst. 2015;74:150-61. https://doi.org/10.1016/j.dss.2015.04.003.
-
20.
James G, Witten D, Hastie T, Tibshirani R. An introduction to statistical learning. Springer; 2013.
-
21.
Mazzocco T, Hussain A. Novel logistic regression models to aid the diagnosis of dementia. Expert Syst Appl. 2012;39(3):3356-61. https://doi.org/10.1016/j.eswa.2011.09.023.
-
22.
Kaplan EL, Meier P. Nonparametric estimation from incomplete observations. J Am Stat Assoc. 1958;53(282):457-81. https://doi.org/10.1080/01621459.1958.10501452.
-
23.
Hess KR, Abbruzzese MC, Lenzi R, Raber MN, Abbruzzese JL. Classification and regression tree analysis of 1000 consecutive patients with unknown primary carcinoma. Clin Cancer Res. 1999;5(11):3403-10. [PubMed ID: 10589751].
-
24.
Stark K. The application of non-parametric techniques to solve classification problems in complex data sets in veterinary epidemiology ? An example. Intell Data Anal. 1999;3(1):23-35. https://doi.org/10.1016/s1088-467x(99)00003-7.
-
25.
Ture M, Tokatli F, Kurt Omurlu I. The comparisons of prognostic indexes using data mining techniques and Cox regression analysis in the breast cancer data. Expert Syst Appl. 2009;36(4):8247-54. https://doi.org/10.1016/j.eswa.2008.10.014.
-
26.
Abadi A, Yavari P, Dehghani-Arani M, Alavi-Majd H, Ghasemi E, Amanpour F, et al. Cox models survival analysis based on breast cancer treatments. Iran J Cancer Prev. 2014;7(3):124-9. [PubMed ID: 25250162].
-
27.
Rezaianzadeh A, Peacock J, Reidpath D, Talei A, Hosseini SV, Mehrabani D. Survival analysis of 1148 women diagnosed with breast cancer in Southern Iran. BMC Cancer. 2009;9:168. [PubMed ID: 19497131]. https://doi.org/10.1186/1471-2407-9-168.
-
28.
Fisher B, Bauer M, Wickerham DL, Redmond CK, Fisher ER, Cruz AB, et al. Relation of number of positive axillary nodes to the prognosis of patients with primary breast cancer. An NSABP update. Cancer. 1983;52(9):1551-7. [PubMed ID: 6352003]. https://doi.org/10.1002/1097-0142(19831101)52:9<1551::AID-CNCR2820520902>3.0.CO;2-3.
-
29.
Galea MH, Blamey RW, Elston CE, Ellis IO. The Nottingham Prognostic Index in primary breast cancer. Breast Cancer Res Treat. 1992;22(3):207-19. [PubMed ID: 1391987]. https://doi.org/10.1007/BF01840834.
-
30.
Silvestrini R, Daidone MG, Luisi A, Boracchi P, Mezzetti M, Di Fronzo G, et al. Biologic and clinicopathologic factors as indicators of specific relapse types in node-negative breast cancer. J Clin Oncol. 1995;13(3):697-704. [PubMed ID: 7884430]. https://doi.org/10.1200/JCO.1995.13.3.697.
-
31.
Todd JH, Dowle C, Williams MR, Elston CW, Ellis IO, Hinton CP, et al. Confirmation of a prognostic index in primary breast cancer. Br J Cancer. 1987;56(4):489-92. [PubMed ID: 3689666]. https://doi.org/10.1038/bjc.1987.230.
-
32.
Baghestani AR, Moghaddam SS, Majd HA, Akbari ME, Nafissi N, Gohari K. Application of a Non-Mixture Cure Rate Model for Analyzing Survival of Patients with Breast Cancer. Asian Pac J Cancer Prev. 2015;16(16):7359-63. [PubMed ID: 26514537]. https://doi.org/10.7314/APJCP.2015.16.16.7359.
-
33.
Nixon AJ, Neuberg D, Hayes DF, Gelman R, Connolly JL, Schnitt S, et al. Relationship of patient age to pathologic features of the tumor and prognosis for patients with stage I or II breast cancer. J Clin Oncol. 1994;12(5):888-94. [PubMed ID: 8164038]. https://doi.org/10.1200/JCO.1994.12.5.888.
-
34.
Fourquet A, Campana F, Zafrani B, Mosseri V, Vielh P, Durand JC, et al. Prognostic factors of breast recurrence in the conservative management of early breast cancer: a 25-year follow-up. Int J Radiat Oncol Biol Phys. 1989;17(4):719-25. [PubMed ID: 2777661]. https://doi.org/10.1016/0360-3016(89)90057-6.
-
35.
Sauerbrei W, Hubner K, Schmoor C, Schumacher M. Validation of existing and development of new prognostic classification schemes in node negative breast cancer. German Breast Cancer Study Group. Breast Cancer Res Treat. 1997;42(2):149-63. [PubMed ID: 9138604]. https://doi.org/10.1023/A:1005733404976.