Investigation of the Hourly and Spatial Patterns of Traffic Offenses During March-April 2019 in Iran Using Bivariate Generalized Additive Models and Integrated Nested Laplace Approximation

Mohammad Fayaz; Alireza Abadi; Alireza Razzaghi; Soheila Khodakarim; Mostafa Hosseini

doi:10.5812/ijhrba-118376

https://doi.org/10.5812/ijhrba-118376

Investigation of the Hourly and Spatial Patterns of Traffic Offenses During March-April 2019 in Iran Using Bivariate Generalized Additive Models and Integrated Nested Laplace Approximation

authors:

Mohammad Fayaz ^{1
, *} , Alireza Abadi ^{2
, 3} , Alireza Razzaghi ⁴ , Soheila Khodakarim ⁵ , Mostafa Hosseini ^{6
, **}

1 Department of Biostatistics, Shahid Beheshti University of Medical Sciences, Tehran, IR Iran

2 Department of Community Medicine, Faculty of Medicine, Shahid Beheshti University of Medical Sciences, Tehran, IR Iran

3 Social Determinants of Health Research Center, Shahid Beheshti University of Medical Sciences, Tehran, IR Iran

4 Road Traffic Injury Research Center, Tabriz University of Medical Sciences, Tabriz, IR Iran

5 Department of Biostatistics, School of Medicine, Shiraz University of Medical Sciences, Shiraz, IR Iran

6 Department of Epidemiology and Biostatistics, School of Public Health, Tehran University of Medical Sciences, Tehran, IR Iran

Corresponding Authors:

International Journal of High Risk Behaviors and Addiction: Vol.11, issue 3; e118376

published online: August 17, 2022

article type: Research Article

received: August 2, 2021

revised: June 26, 2022

accepted: July 2, 2022

How To Cite Fayaz M, Abadi A, Razzaghi A, Khodakarim S, Hosseini M. Investigation of the Hourly and Spatial Patterns of Traffic Offenses During March-April 2019 in Iran Using Bivariate Generalized Additive Models and Integrated Nested Laplace Approximation. Int J High Risk Behav Addict. 2022;11(3):e118376. https://doi.org/10.5812/ijhrba-118376.

Abstract

Background:

The control, management, and prevention of driving accidents and risky driving are regarded as concerns for numerous countries, according to the World Health Organization. In this regard, many technologies, such as count stations, are recommended. They count traffic offenses, such as speeding and unsafe distance, hourly and daily, and have different patterns according to the hour of the day and the location.

Objectives:

This study aimed to investigate the risky driving behaviors according to traffic offenses in Iran and estimate their hourly and spatial patterns using generalized additive models (GAMs) and stochastic partial differential equation methods.

Materials and Methods:

There were 2,316 count data stations for one month within March-April 2019. This study estimated the hourly average of each traffic offense, Pearson’s and Spearman’s correlations, and the energy statistics for testing the bivariate normal distribution. There are five distributions, such as univariate Poisson, quasi-likelihood Poisson, Gaussian, location-scale Gaussian, and bivariate Gaussian in GAMs, to study the hourly patterns which were compared to the mean squared error (MSE) and correlation.

Results:

The hourly average of total vehicles and number of speeding and unsafe distance offenses per count station had positive skew distributions with mean values equal to 347 ± 456, 22.5 ± 44.2, and 65.9 ± 150, respectively. The correlation between traffic offenses in most provinces was significant, not large, and different. The GAM with the bivariate Gaussian distribution had the best performance according to the MSE and correlation. It revealed three hourly patterns for count predictions; the first was that speeding is higher than unsafe distances; the second was that unsafe distances are higher than speeding; the third was that speeding and unsafe distances do not have a specific pattern in some hours. The percentage of speeding was higher in the central, northeast, and southeast regions than in other parts of Iran, and the percentage of unsafe distances was higher for the north, northwest, west, and some parts of the southwest than in other parts of Iran, respectively.

Conclusions:

The hourly pattern of traffic offenses exists and has a complex structure. The spatial pattern of traffic offenses shows the riskiest points in Iran.

Keywords

Iran Aggressive Driving Traffic Generalized Additive Model Stochastic Processes

1. Background

The traffic and speed cameras and count stations near the roads are some technologies developed to manage, control, and predict traffic status in different countries. These devices produce massive datasets hourly and daily, making them one of the primary resources for discovering patterns and relationships. For example, there are diverse indices, including the count of driving offenses and total vehicles based on their type, which could be considered (1, 2). According to the global status report on road safety by the World Health Organization, driving accidents and risky driving are among the remarkable causes of death worldwide (2).

This study investigated the hourly and spatial patterns of driving offenses using two advanced statistical methods, respectively. Firstly, the generalized additive model (GAM) extended the generalized linear model (GLM) idea by adding the smoothing functions, such as cubic regression splines for estimating, hypothesis testing, and confidence interval for coefficients. The GAM was enhanced to capture complex and nonlinear relationships between response variables and covariates (3-5). Secondly, the stochastic partial differential equation (SPDE) method is one of the techniques to study spatial variability with the integrated nested Laplace approximation (R-INLA) (6).

2. Objectives

The traffic offenses dataset from count stations is a source for studying driving behaviors in Iran. The speeding and unsafe-distance indices are the indicators of risky driving for the control and prevention for which governments worldwide have different laws (2). Firstly, this study estimated the hourly average of each traffic offense per count station national-wide and province-wise. It shows how many traffic offenses occurred on average in each count station hourly. Secondly, the correlations and bivariate distribution between speeding and unsafe distance province-wise offenses were evaluated by Pearson’s and Spearman’s correlation coefficients and bivariate normal test based on the energy statistics, respectively. Thirdly, this study modeled the nonlinear relationship between the number of traffic offenses and the time of a day for each province with GAMs separately. Finally, this study introduced the percentage of traffic offenses among all transported vehicles as a key index to study the risky behavior of drivers on roads and investigated their spatial variability with SPDE. Moreover, temporal variability for four different ranges of hours was evaluated.

3. Materials and Methods

3.1. Population and Dataset

The population of this study was all count data stations near the interprovincial roads of Iran, which are available online from Iran Road Maintenance and Transportation Organization on the website of the Ministry of Roads and Urban Development (rmto.ir). All days of the first Iranian month, Farvardin, were considered in this analysis (31 days within 3/21/2019 to 4/20/2019). The number of individuals traveling between provinces increases in the first and second weeks of this month due to the Iranian New Year holidays. The condition of the roads gets back to regularly slow during the third and fourth weeks of this month. Therefore, the risky driving behavior of most Iranians could be estimated in this month.

The count data stations record hourly and daily different indices, such as total vehicles and the number of speeding and unsafe distance offenses. There were 31 separated provincial datasets. The active count stations record 60 minutes an hour, and only 2,316 count data stations remain. The count of unsafe distance offenses is the total number of vehicles with a distance shorter than 2 seconds between them. The count of speeding is the total number of vehicles on the road with a speed higher than the speed control limit (rmto.ir).

3.2. Statistical Analysis

3.2.1. Testing the Multivariate Normal Distribution

In order to study the bivariate distribution of these two traffic offenses, this study chose the energy test statistics that have the best performance among multivariate Gaussian distribution tests (7, 8). The observation Z ∈ R^d has a multivariate Gaussian distribution N_d (0, I_d) with the mean vector of 0 and the variance-covariance matrix I_d (9) as follows:

Equation 1.

E {|Z - Z^{'}|}_{d} = \sqrt{2} E {|Z|}_{d} = 2 \frac{Γ (\frac{d + 1}{2})}{Γ (\frac{d}{2})}

The y₁,…, y_n are the standardized elements of the sample. The energy test statistics for the d-distribution standard normal are as follows:

Equation 2.

n ε_{n, d} = n (\frac{n}{2} \sum_{j = 1}^{n} E {|y_{i} - Z|}_{d} - 2 \frac{Γ (\frac{d + 1}{2})}{Γ (\frac{d}{2})} - \frac{1}{n^{2}} \sum_{j, k = 1}^{n} {|y_{j} - y_{k}|}_{d})

And

Equation 3.

E {|a - Z|}_{d} = \frac{\sqrt{2} Γ (\frac{d + 1}{2})}{Γ (\frac{d}{2})} + \sqrt{\frac{2}{π}} \sum_{k = 0}^{\infty} \frac{{(- 1)}^{k}}{k! 2^{k}} \frac{{|a|}_{d}^{2 k + 2}}{(2 k + 1) (2 k + 2)} \frac{Γ (\frac{d + 1}{2}) Γ (k + \frac{3}{2})}{Γ (k + \frac{d}{2} + 1)}

For computation, the sample of observation is standardized based on the mean and correlation matrix. The obtained test statistic $n ε {\hat{}}_{n, d}$ has limited distributions, such as n $ε$ _n,d, with the rejection region on the upper tail. The $n ε {\hat{}}_{n, d}$ statistics are compared to the repeated energy statistics by the Monte Carlo sampling and 200 iterations from standardized normal with the same dimensions.

3.2.2. Correlation Tests

The correlation between the two random variables Y₁ and Y₂ or ρ₁₂ was assessed with the maximum likelihood estimation of the Pearson product-moment correlation coefficient if their distribution was bivariate normal. When the joint distribution of the two random variables was not multivariate normal, the correlation was evaluated utilizing Spearman’s Rank correlation coefficient. In this test, the ranks of Y₁ and Y₂ are R₁ and R₂ for calculation, respectively (10).

3.2.3. Generalized Additive Model

The GAM is a GLM with a set of smoothing functions of covariates. The general form is as follows:

Equation 4.

g (μ_{i}) = A_{i} θ + f_{1} (x_{1 i}) + f_{2} (x_{2 i}) + \dots

where μ_i ≡ E (Y_i) and Y_i ~ EF (μ_i, ϕ). The response term is Y_i with the exponential family, a mean of μ_i, and the scale parameters of ϕ. The A_i is related to the parametric part of the model, and θ represents a vector related to the parameters. The f_i is the smoothing function of the covariate x_k (4). This study considered and compared the five distributions of univariate Poisson, univariate quasi-Poisson, univariate Gaussian, univariate location-scale Gaussian, and bivariate Gaussian for Y_i. There are two models for each distribution, with the response variable in models 1 and 2 being the number of speeding and unsafe distance offenses, respectively. The only covariate in the model is the hour of the day, and the smoothing function f₁(x) is a cubic regression spline with k = 20. The mean squared error (MSE) and correlation between observations and fitted values are the criteria for choosing the best model (4, 5).

3.2.4. Spatial Data Analysis

The response variable was the percentage of total speeding and unsafe distances in the total traffic during one month for each count station, respectively. The count station location has some information that accounts for this model. The Y_i refers to the percentage of each traffic offense at count station s_i and has a Gaussian distribution as follows:

Equation 5.

Y_{i} ~ N (μ_{i}, σ^{2}), i = 1, \dots, 2316

Equation 6.

μ_{i} = β_{0} + Z (s_{i})

where Z(.) indicates a spatially structured random effect with zero-mean Gaussian process and Matérn covariance. The fitting method was the SPDE approach with R-INLA. The mesh was constructed with different margins to approximate Y_i to a discrete Gaussian Markov random field. The models predict the lower and upper limits with 95% credible intervals, and the result is a map plot (6). All the statistical analyses were performed using R 4.0.2 (r-project.org) with mgcv, energy, geoR, maps, rgdal, maptools, sf, viridis, and ggplot2 packages (11-18).

4. Results

Table 1 shows the results of descriptive statistics and p-values for the bivariate normal test based on the energy statistics and correlation coefficients. Diverse factors were associated with driving offenses, among which only the time of day as a spline function was considered in this study. Table 2 shows the results of fitting 1) univariate GAM with quasi-Poisson distribution and 2) bivariate Gaussian GAM (other models, including univariate Poisson, univariate Gaussian, and univariate location-scale Gaussian, in Appendix 1). These two models had the best performance among their Poisson-related and Gaussian-related families according to the MSE and correlation indices.

Table 1.

Descriptive Statistics ^a

Provinces	Number of Count Stations	Hourly Average per Station (SD)		P-Value of Bivariate Normal Test ^b	Correlation
Provinces	Number of Count Stations	Speeding	Unsafe Distance	P-Value of Bivariate Normal Test ^b	Pearson	Spearman
Ardebil	64	12.2 (12.3)	33.3 (29.2)	< 0.05	0.16 (< 0.05)	0.29 (< 0.05)
Isfahan	120	26.5 (35.4)	30.3 (50.2)	> 0.05	0.26 (< 0.05)	0.50 (< 0.05)
Alborz	40	99.4 (197.6)	320.8 (555.8)	< 0.05	0.32 (< 0.05)	0.49 (< 0.05)
Ilam	48	5.5 (5.7)	14.5 (17.4)	> 0.05	0.21 (< 0.05)	0.46 (< 0.05)
West Azarbayjan	90	17.9 (19.2)	40 (28.6)	< 0.05	0.25 (< 0.05)	0.46 (< 0.05)
East Azarbayjan	82	15.4 (23.5)	18.2 (63.6)	< 0.05	-0.01 (0.11)	0.08 (< 0.05)
Bushehr	52	16.9 (14.8)	53.5 (68)	< 0.05	0.26 (< 0.05)	0.30 (< 0.05)
Tehran	103	49.5 (79.3)	259.6 (334.7)	< 0.05	0.27 (< 0.05)	0.41 (< 0.05)
Chaharmahal and Bakhtiari	62	23.7 (24.8)	26 (21.3)	> 0.05	0.46 (< 0.05)	0.49 (< 0.05)
South Khorasan	72	20.5 (16.4)	13.9 (12.7)	> 0.05	0.51 (< 0.05)	0.61 (< 0.05)
Razavi Khorasan	131	19.6 (31.5)	70 (133.9)	< 0.05	0.30 (< 0.05)	0.48 (< 0.05)
North Khorasan	47	12.6 (17.4)	32.5 (27.5)	> 0.05	0.33 (< 0.05)	0.26 (< 0.05)
Khuzestan	104	14.5 (17.8)	34.7 (31.2)	> 0.05	0.16 (< 0.05)	0.41 (< 0.05)
Zanjan	74	7.3 (8.7)	40.5 (52.5)	> 0.05	0.38 (< 0.05)	0.48 (< 0.05)
Semnan	54	43.9 (49.3)	33.1 (36.2)	> 0.05	0.58 (< 0.05)	0.69 (< 0.05)
Sistan and Balouchestan	70	26.2 (24)	1.2 (1.3)	> 0.05	0.50 (< 0.05)	0.44 (< 0.05)
Fars	126	33.7 (46.1)	74 (110.9)	> 0.05	0.21 (< 0.05)	0.35 (< 0.05)
Qazvin	57	14.8 (25.1)	171.5 (268.2)	> 0.05	0.25 (< 0.05)	0.50 (< 0.05)
Qom	76	49 (74)	82.4 (124.3)	> 0.05	0.16 (< 0.05)	0.20 (< 0.05)
Kordestan	52	7.6 (9.9)	26.9 (28)	< 0.05	0.30 (< 0.05)	0.37 (< 0.05)
Kerman	107	13.4 (13.4)	19.6 (17.2)	< 0.05	0.27 (< 0.05)	0.33 (< 0.05)
Kermanshah	72	9.8 (12.1)	42.2 (47.9)	< 0.05	0.32 (< 0.05)	0.52 (< 0.05)
Kohkilouye and Boyerahmad	28	7.1 (8.5)	24.6 (19.7)	< 0.05	0.34 (< 0.05)	0.50 (< 0.05)
Golestan	52	13.1 (24.6)	78.5 (109.9)	< 0.05	0.00 (0.65)	0.29 (< 0.05)
Gilan	84	9.8 (15)	193 (179.2)	< 0.05	0.09 (< 0.05)	0.30 (< 0.05)
Lorestan	62	11.7 (12.5)	28.7 (31.8)	< 0.05	0.38 (< 0.05)	0.49 (< 0.05)
Mazandaran	102	23.7 (34.7)	111.6 (164)	> 0.05	0.13 (< 0.05)	0.32 (< 0.05)
Markazi	64	30.6 (29.7)	56.7 (64.2)	< 0.05	0.36 (< 0.05)	0.47 (< 0.05)
Hormozgan	72	27.5 (31.7)	37.4 (37.9)	< 0.05	0.49 (< 0.05)	0.48 (< 0.05)
Hamedan	71	15.3 (20.3)	44.4 (74.9)	> 0.05	0.47 (< 0.05)	0.69 (< 0.05)
Yazd	78	19.6 (32.6)	19.8 (40.8)	< 0.05	0.58 (< 0.05)	0.53 (< 0.05)

Abbreviation: SD, standard deviation.

^aThe hourly average per station of offenses, the P-value for the normality test of the joint normal distribution of speeding and unsafe distance, the correlation between speeding and unsafe distance with Pearson and Spearman, and their P-Values by provinces of Iran.

^b Based on the energy statistics.

Table 2.

Mean Squared Error and Correlation Between Observed Values and Predicted Values by Provinces in Three Generalized Additive Models

Provinces	Univariate Quasi-Poisson				Bivariate Gaussian
	MSE		COR		MSE		COR
	Speeding	Unsafe Distance	Speeding	Unsafe Distance	Speeding	Unsafe Distance	Speeding	Unsafe Distance
Ardebil	431.58	5585.6	0.26	0.37	313.039	3886.618	0.2655	0.4164
Isfahan	4234.72	9435.8	0.25	0.24	3305.632	7955.29	0.2588	0.2578
Alborz	100001.65	741558.34	0.11	0.22	86774.854	576048.427	0.1071	0.2286
Ilam	115.86	2336.48	0.28	0.24	84.528	1887.848	0.2714	0.253
West Azarbayjan	1083.11	2514.08	0.23	0.3	1544.517	12434.603	0.2564	0.2809
East Azarbayjan	1943.81	15195.81	0.25	0.26	839.992	1988.403	0.2496	0.3423
Bushehr	779.4	14589.36	0.22	0.29	540.01	10785.777	0.2256	0.3195
Tehran	15866.28	354773.14	0.17	0.3	12766.231	242816.189	0.1775	0.3289
Chaharmahal and Bakhtiari	1664.66	2716.23	0.3	0.41	1105.088	1737.031	0.3112	0.4543
South Khorasan	1319.27	1133.26	0.33	0.32	834.305	873.05	0.3386	0.3355
Razavi Khorasan	2241.12	50497.25	0.18	0.22	1682.416	40515.689	0.1797	0.2487
North Khorasan	936.37	5419.72	0.16	0.38	767.099	3592.478	0.1647	0.4066
Khuzestan	978.81	6959.98	0.2	0.33	737.537	4672.25	0.1983	0.3649
Zanjan	229.03	19909.58	0.18	0.24	193.617	17284.791	0.1796	0.2557
Semnan	10017.67	11546.95	0.25	0.24	7481.894	9765.432	0.2607	0.2609
Sistan and Balouchestan	2478.86	12.47	0.34	0.3	1363.401	10.218	0.3528	0.3227
Fars	5385.19	39761.19	0.21	0.27	4162.456	31543.184	0.2155	0.2845
Qazvin	2263.28	360868.29	0.14	0.24	1600.491	244795.473	0.1557	0.218
Qom	16924.48	61534.78	0.23	0.27	13419.011	49202.503	0.2369	0.2833
Kordestan	235.64	3365.31	0.17	0.38	197.928	2299.921	0.1735	0.4272
Kerman	659.95	2465.71	0.26	0.34	419.746	1635.215	0.2572	0.3666
Kermanshah	744.38	11365.21	0.17	0.32	665.794	8546.778	0.1719	0.3573
Kohkilouye and Boyerahmad	339.82	5697.06	0.25	0.4	238.177	3585.047	0.2614	0.4133
Golestan	1439.64	35333.35	0.18	0.33	1237.653	24184.02	0.1821	0.3728
Gilan	508.84	143528.05	0.14	0.37	439.298	88628.456	0.1437	0.4038
Lorestan	483.89	6004.13	0.24	0.31	365.061	4710.623	0.2407	0.3312
Mazandaran	4042.83	77117.08	0.14	0.31	3398.741	55020.8	0.1454	0.3335
Markazi	3435.27	24601.29	0.28	0.3	2382.4	19328.955	0.2917	0.3174
Hormozgan	3159.51	8827.06	0.22	0.29	2209.037	6432.453	0.2174	0.2983
Hamedan	1741.22	22891.93	0.23	0.27	1362.917	18492.39	0.2293	0.2981
Yazd	2615.35	7838.14	0.16	0.18	2153.476	7174.672	0.1643	0.1896

Abbreviations: MSE, mean squared error; COR, correlation.

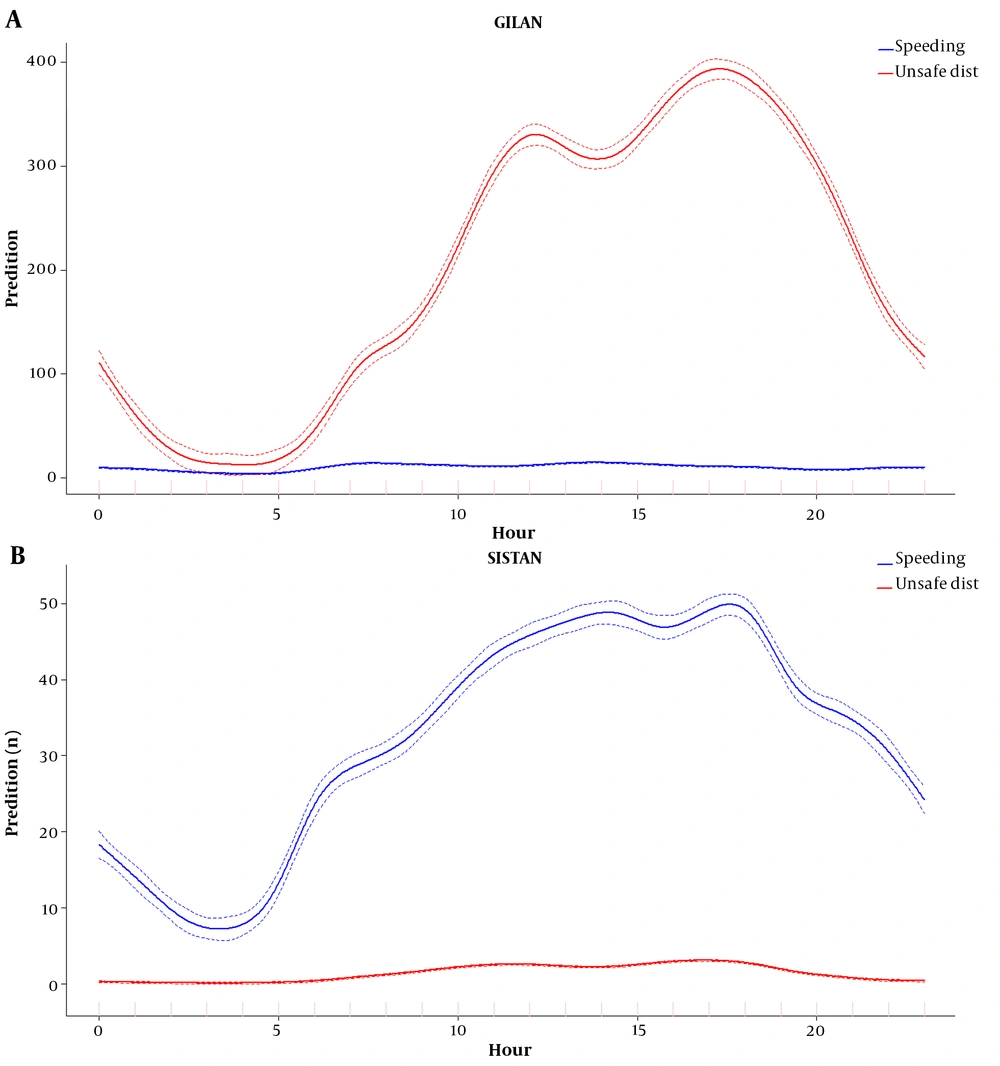
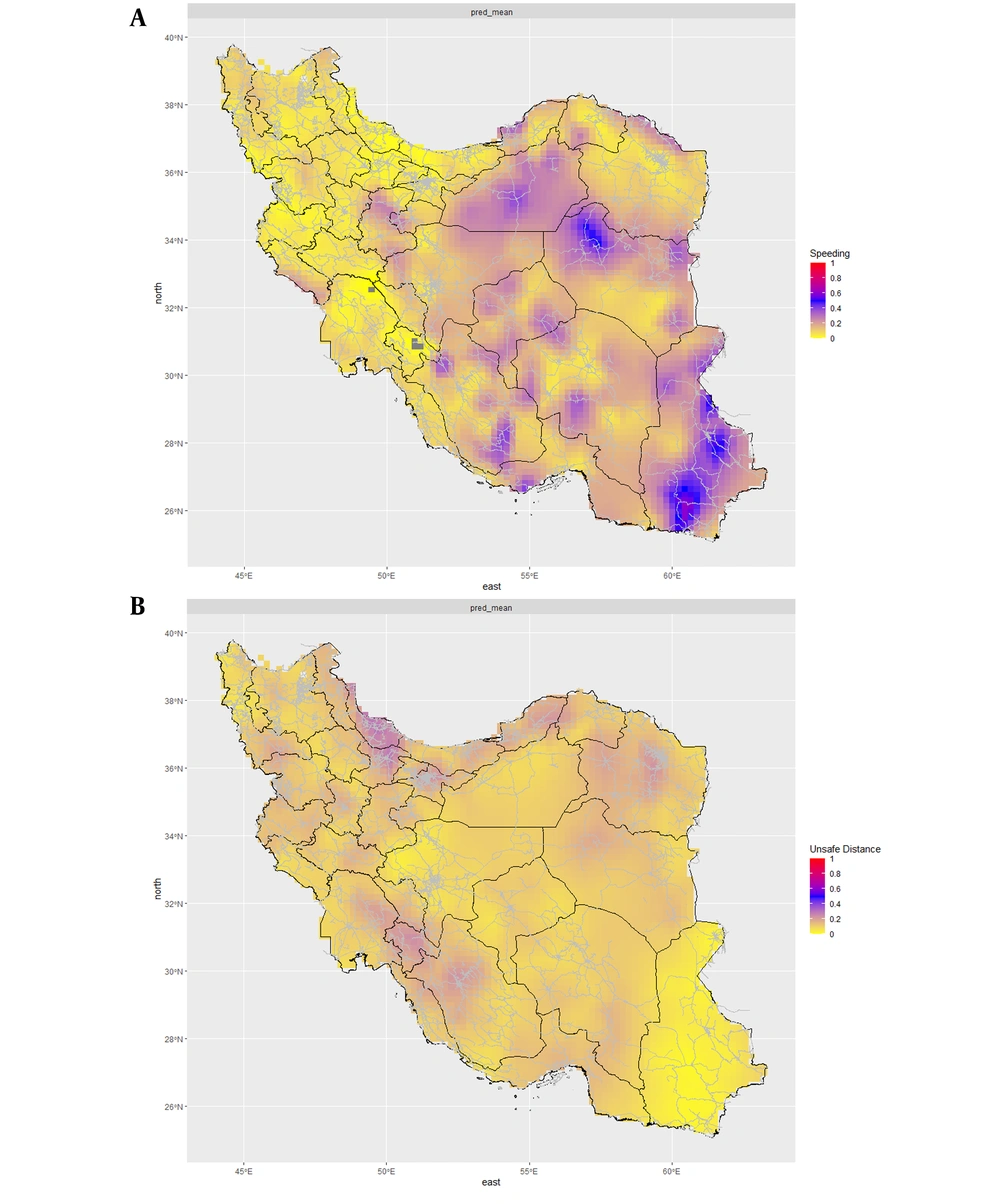
Figure 1 shows the predicted responses for the bivariate Gaussian model in Sistan and Baluchestan, and Gilan provinces, Iran. The patterns of these two plots were in contradiction. All figures for both univariate quasi-Poisson and bivariate Gaussian GAM models are presented in the appendix (Appendix 2). Figure 2 illustrates the predicted percentage of speeding and unsafe distance offenses with their spatial patterns in Iran. The two plots had a different pattern that indicated the percentage of speeding is higher in the central, northeast, and southeast regions than in other parts of Iran. The predicted percentage of speeding was higher than unsafe distance, indicating that speeding is high in Iran. The predicted percentage of unsafe distance with a range of 20 - 40% was higher for north, northwest, west, and some parts of southwest than other parts of Iran. These plots were produced with the triangulated mesh method. The other mesh method is available for comparison in Appendix 3.

Figure 1.

Estimated number of speeding (blue) and unsafe distance (red) offenses in A, Gilan; and B, Sistan and Balouchestan, Iran

Figure 2.

Mean prediction of A, speeding; and B, unsafe distance rates (within 0 (yellow) and 1 (red))

The temporal and hourly patterns of the predicted percentage for traffic offenses are available in Appendix 4.1 and Appendix 4.2, respectively. There were four intervals of 6 hours, including 0 - 5, 6 - 11, 12 - 17, and 18 - 23. According to Appendix 4.1, the predicted percentage of speeding was the highest at 0 - 5. On the other hand, Appendix 4.2 shows that the predicted percentage of unsafe distance was the lowest at 0 - 5 and had the highest value at 12 - 17 (Appendix 4.1 and Appendix 4.2).

5. Discussion

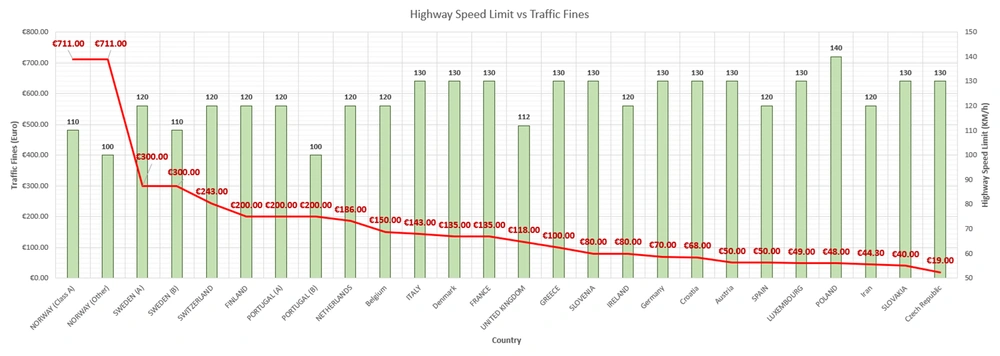
The speed limit and speeding fines for intercity highways are different in European countries and Iran. As illustrated in Figure 3, Norway has the highest speeding fines (€711), and the Czech Republic has the lowest speeding fines (€19) among other countries, respectively. In some countries, the speeding limits are different based on the two lanes or other roads (Norway), winter and other seasons (Sweden and Finland), rainy and other weather conditions (Luxembourg and Italy), and free speed (Germany). The traffic fines for speeding in Iran within 2021 - 2022 is 2,100,000 Iranian Rial (IR) (equivalently about €44.30 if €1 = 47,377 IRR (i.e., official governmental NIMA, the Central Bank of the Islamic Republic of Iran exchange rate) and about €6.72 if €1 = 312,480 IRR (i.e., unofficial open market exchange rate) in Q1 2022). Nevertheless, this comparison of speeding fines is simple and naive according to the different purchasing power parity and gross domestic product between countries; therefore, it is suggested to compare them to new indices, such as Big Mac Index, in future studies (19). The Figure 3 dataset is made from speedingeurope.com and rahvar120.ir datasets.

Figure 3.

Bar chart (green) of highway speed limit (km/h) and line chart (red) of speeding traffic fines (euro) by countries

A significant relationship has been reported between road traffic accidents (RTA) and time (e.g., the time of the day) in Yazd, Iran, during the New Year holidays and summer (20). It has been the other study for these holidays in the six most populous provinces of Iran, namely Fars, Khorasan Razavi, Tehran, Isfahan, Kerman, and Khuzestan, within 2011 - 2015, indicating that Fars and Khorasan Razavi, with attractive tourist sites, have different high RTA among others (21). The mortality rate due to traffic accidents is higher in Iran at midnight and summer (22, 23) and in spring and summer in Shiraz (24) than in other times. The present study showed that the speeding rate was higher from midnight to early morning throughout Iran. This finding might be due to the existence of black spots with low and not uniform lighting on the roads (25). It also suggests that risky driving, not darkness, is the main reason for accidents (26). However, there are some exceptions; for example, in the south of Iran (27) and Yasuj (28), the rate of accidents during the day is higher than at night. The provinces in the south of Iran are located in the warmest region in the country, with an average daily high temperature. The high rate of accidents during the day in these provinces might be due to heat stress on drivers. A similar finding was reported in a study in Saudi Arabia (29) and high ambient temperatures in Spain (30). The percentage of RTA in Fars, Isfahan, Ilam, and the southeast region of Iran has a nonlinear trend in 24 hours with different peaks of speeding and unsafe distance (26, 31-34).

The rate of unsafe distance offense is almost high in Kermanshah, Iran, and it can be added as a new risk factor of RDA in this province (35). The highest rate of mortality for drivers, passengers, and pedestrians has been reported during 13:00 - 18:00 in the west of Iran (36), 18:00 - 20:00 in Mashhad (37), and 16:00 - 18:00 in the southeast of Iran (38). The findings of other studies showed that most of the collisions occurred in the early hours of the night. A part of these collisions is due to poor visibility. Inadequate visibility has a key role in crashes involving pedestrians, motorcyclists, cyclists, and drivers (39). Moreover, crashes at dark hours cause severe injuries (40, 41). According to the findings of a meta-analysis study, the odds ratio of mortality in dark-hour crashes is 53% higher than in day-hour crashes (42). Consequently, traffic offenses might have a relationship with RTA-related mortality. In this regard, this study suggests adding traffic offenses statistics to the Iranian Integrated Road Traffic Injury Registry (43, 44) and RTA studies. The other risk factors are the spatial variations of traffic offenses and accidents, seatbelt and helmet status, gender, age group (45), and climatic conditions, such as fog in the north of Iran (46).

The traffic fines and risky driving in Iran are studied in different ways, including the relationship between the number of traffic offenses and fuel costs within 2011 - 2019 (47), the relationship between increasing traffic fines policies and the road traffic law enforcement (48), the prevalence and determination of speeding in Iran (49), the comparison study of traffic fines in Iran and other countries (50), risky driving fined by police in 2006 and 2007 in Tehran (51), the effect of cameras on speeding behavior of taxi drivers in two highways (52), and aggressive violations (e.g., “sound horn to indicate your annoyance”, “get angry, give chase”, and “aversion, indicating hostility”). Moreover, Iran and Great Britain, the Netherlands, and Finland are among the countries with higher speeding violations than other countries, such as Greek and Turkey (53). In addition, visual, perceptual, and cognitive capabilities and physiological condition of drivers (e.g., Barkley’s Attention Deficit Hyperactivity Disorder Screening Test, Risk Perception Questionnaire, Risk Taking Questionnaire, Sensation Seeking Scale Survey, and Driver Behavior Questionnaire), among other factors in SHRP2 naturalistic driving study, are assessed in the USA (54).

Advanced and sophisticated statistical methods are in demand for traffic-related datasets. The GAMs are among the statistical models that can be used for complex relationships, such as risky driving in Iran (4) (e.g., driving offenses near public places, such as airports (1)). The bivariate structure of the response can estimate the correlation and compare the traffic offenses between provinces at distinct times of the day (5). It also calculates the peak hours and 95% confidence interval with their pattern for each province. The Getis-Ord General G* statistic in geographically weighted regression models revealed that the hotspot for fatal pedestrian accidents is in Mazandaran, Iran, and it is more common in Yazd, East Azerbaijan, and Ardebil (55). Future studies can investigate clustering methods, statistical learning methods (56), functional data analysis (57), and GAM for location, scale, and shape techniques to estimate the exact distribution with many parameters and their estimation for the underlying distribution (58).

5.1. Conclusions

The present study concluded that the risky driving behaviors due to traffic offenses can be estimated straightforwardly at different times and locations and add new information about the time of the days and roads that have not registered or occurred any traffic accidents. In this regard, they are predictive models. The geographical status of the roads, such as mountains or deserts, is shown to be related to the type of traffic offenses. For example, speeding violations on desert roads are higher than mountain roads, and unsafe distance violations on mountain roads are higher than desert roads. The day-night, rush hours, and holidays are the main time-related factors for occurring traffic offenses. The future direction of this study is to investigate the relationships between the percentage of traffic offenses and traffic accident occurrence, climate status (e.g., raining, foggy, and sunny), and holidays and restrictions (e.g., coronavirus disease 2019 restriction) on all roads in different times of the day.

In highway safety research, crash modification factors and safety performance are introduced based on the traffic volume and road characteristics, and different statistical methods are proposed to estimate them (59, 60). Therefore, defining new and easy-to-compute indices is needed for future studies to measure and model the percentage of risky driving. This study had some limitations. Firstly, the police statistics have crime classification errors (e.g., some errors in detecting speeding and unsafe distance) and systematic errors (e.g., the failure of count stations in some hours) (61). Secondly, the statistics on traffic accidents are not publicly available.

Footnotes

Authors' Contribution: Mohammad Fayaz developed the original idea and the protocol, abstracted and analyzed the data, wrote the manuscript, and was a guarantor. Alireza Abadi, Soheila Khodakarim, Alireza Razzaghi, and Mostafa Hosseini contributed to the preparation of the manuscript.
Conflict of Interests: The authors declare that there is no conflict of interest in this study.
Data Reproducibility: The data presented in this study are openly available in one of the repositories or will be available on request from the corresponding author by this journal representative at any time during submission or after publication. Otherwise, all the consequences of possible withdrawal or future retraction will be with the corresponding author.
Funding/Support: There was no funding/support for this manuscript.

References

1.
Fayaz M, Abadi AR, Khodakarim S, Hoseini MR, Razzaghi AR. The Data-Driven Pattern for Healthy Behaviors of Car Drivers Based on Daily Records of Traffic Count Data from 2018 to 2019 near Airports: A Functional Data Analysis. JP J Biostat. 2020;17(2):539-57. https://doi.org/10.17654/bs017020539.
2.
World Health Organization. Global status report on road safety 2018: summary. Geneva: World Health Organization; 2018, [cited 2022]. Available from: https://www.who.int/publications/i/item/WHO-NMH-NVI-18.20.
3.
Hastie T, Friedman J, Tibshirani R. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. New York, NY: Springer Series in Statistics; 2001.
4.
Wood SN. Generalized Additive Models: An Introduction with R. New York: CRC Press; 2017. https://doi.org/10.1201/9781315370279.
5.
Wood SN, Pya N, Säfken B. Smoothing Parameter and Model Selection for General Smooth Models. J Am Stat Assoc. 2016;111(516):1548-63. https://doi.org/10.1080/01621459.2016.1180986.
6.
Moraga P. Geospatial Health Data: Modeling and Visualization with R-INLA and Shiny. New York: Chapman and Hall/CRC; 2019. https://doi.org/10.1201/9780429341823.
7.
Chen W, Genton MG. Are You All Normal? It Depends. Ithaca, NY: arXiv; 2020, [cited 2022]. Available from: https://www.researchgate.net/publication/343877013.
8.
Joenssen DW, Vogel J. A power study of goodness-of-fit tests for multivariate normality implemented in R. J Stat Comput Simul. 2012;84(5):1055-78. https://doi.org/10.1080/00949655.2012.739620.
9.
Székely GJ, Rizzo ML. A new test for multivariate normality. J Multivar Anal. 2005;93(1):58-80. https://doi.org/10.1016/j.jmva.2003.12.002.
10.
Kutner MH. Applied linear statistical models. New York: McGraw-Hill Irwin; 2005.
11.
Rizzo ML, Szekely GJ, Rizzo MM. Package ‘energy’. 2021. Available from: https://cran.r-project.org/web/packages/energy/energy.pdf.
12.
Wood SN. mgcv: GAMs and generalized ridge regression for R. R News. 2001;1/2:20-5.
13.
Garnier S, Ross N, Rudis R, Camargo AP, Sciaini M, Cédric S. viridis - Colorblind-Friendly Color Maps for R. Newark, NJ: Sjmgarnier; 2021, [cited 2022]. Available from: https://sjmgarnier.github.io/viridis/.
14.
Becker RA, Wilks AR, Ray Brownrigg R, Minka TP, Deckmyn A. maps: Draw Geographical Maps. Wien, Austria: The Comprehensive R Archive Network; 2018, [cited 2022]. Available from: https://pdf4pro.com/view/maps-draw-geographical-maps-62d0bf.html.
15.
Bivand R, Lewin-Koh N, Pebesma E, Archer E, Baddeley A, Bearman N, et al. maptools: Tools for Handling Spatial Objects. Wien, Austria: The Comprehensive R Archive Network; 2022, [cited 2022]. Available from: https://cran.r-project.org/web/packages/maptools/index.html.
16.
Ribeiro Jr PJ, Diggle P, Christensen O, Schlather M, Bivand R, Ripley B, et al. geoR: Analysis of Geostatistical Data. Wien, Austria: The Comprehensive R Archive Network; 2022, [cited 2022]. Available from: https://cran.r-project.org/web/packages/geoR/index.html.
17.
Bivand R, Keitt T, Rowlingson B, Pebesma E, Sumner M, Hijmans R, et al. rgdal: Bindings for the 'Geospatial' Data Abstraction Library. Wien, Austria: The Comprehensive R Archive Network; 2021, [cited 2022]. Available from: https://cran.r-project.org/web/packages/rgdal/index.html.
18.
Wickham H. ggplot2: Elegant Graphics for Data Analysis. New York: Springer; 2009. https://doi.org/10.1007/978-0-387-98141-3.
19.
Clements KW, Si J. Simplifying The Big Mac Index. J Int Financial Manag Account. 2017;28(1):86-99. https://doi.org/10.1111/jifm.12058.
20.
Lotfi M, Montazeri M, Lashkardoost H, Shamsi F, Askari M, Hamedi E, et al. Road traffic accidents in Yazd province, Iran: A longitudinal study (2012–2016). Arch Trauma Res. 2018;7(2):68-72. https://doi.org/10.4103/atr.atr_9_18.
21.
Besharati MM, Azizi Bondarabadi M, Memariyan M, Tavakoli Kashani A. Patterns of road traffic fatalities in the six most populous provinces of Iran, 2011–2015. Arch Trauma Res. 2019;8(3):177-81. https://doi.org/10.4103/atr.atr_91_18.
22.
Sadeghi-Bazargani H, Ayubi E, Azami-Aghdash S, Abedi L, Zemestani A, Amanati L, et al. Epidemiological Patterns of Road Traffic Crashes During the Last Two Decades in Iran: A Review of the Literature from 1996 to 2014. Arch Trauma Res. 2016;5(3). e32985. [PubMed ID: 27800461]. [PubMed Central ID: PMC5078874]. https://doi.org/10.5812/atr.32985.
23.
Shahbazi F, Soori H, Khodakarim S, Ghadirzadeh MR, Hashemi Nazari SS. Analysis of mortality rate of road traffic accidents and its trend in 11 years in Iran. Arch Trauma Res. 2019;8(1):17-22. https://doi.org/10.4103/atr.atr_72_18.
24.
Ghaem H, Hajipour M, Tababataee HR, Yadollahi M, Izanloo F. Time Series Analysis of Mortalities Resulting from Car Accidents in the Injured Individuals Hospitalized in Shiraz Shahid Rajaee Hospital During 2010 - 2016. Trauma Mon. 2018;23(1). e13573. https://doi.org/10.5812/traumamon.13573.
25.
Mohan A, Landge VS. Identification of Accident Black Spots on National Highway. Int J Civ Eng Technol. 2017;8(4):588-96.
26.
Mohammadi G. The pattern of fatalities by age, seat belt usage and time of day on road accidents. Int J Inj Contr Saf Promot. 2009;16(1):27-33. [PubMed ID: 19058047]. https://doi.org/10.1080/17457300802406963.
27.
Rakhshani T, Rakhshani F, Asadi ZS, Hadiabasi M, Khorramdel K, Zarenezhad M. Study of the pattern of mortality caused by Traffic Accidents (TAs) in The South of Iran. J Pak Med Assoc. 2016;66(6):644-9. [PubMed ID: 27339561].
28.
Rakhshani T, Kashfi M, Amirian I, Ebrahimi M, Hashemi Nazari S. Epidemiology of Fatal Road Traffic Accidents in Iran, Yasouj, 2014-2015. J Health Sci Surveill Syst. 2018;6(1):29-35.
29.
Nofal FH, Saeed AA. Seasonal variation and weather effects on road traffic accidents in Riyadh city. Public Health. 1997;111(1):51-5. [PubMed ID: 9033225]. https://doi.org/10.1038/sj.ph.1900297.
30.
Basagana X, Escalera-Antezana JP, Dadvand P, Llatje O, Barrera-Gomez J, Cunillera J, et al. High Ambient Temperatures and Risk of Motor Vehicle Crashes in Catalonia, Spain (2000-2011): A Time-Series Analysis. Environ Health Perspect. 2015;123(12):1309-16. [PubMed ID: 26046727]. [PubMed Central ID: PMC4671248]. https://doi.org/10.1289/ehp.1409223.
31.
Hasanzadeh J, Moradinazar M, Najafi F, Ahmadi-Jouybary T. Trends of Mortality of Road Traffic Accidents in Fars Province, Southern Iran, 2004 - 2010. Iran J Public Health. 2014;43(9):1259-65. [PubMed ID: 26175980]. [PubMed Central ID: PMC4500428].
32.
Mansouri M, Javad Kargar M. Analysis and Monitoring of the Traffic Suburban Road Accidents Using Data Mining Techniques; A Case Study of Isfahan Province in Iran. Open Transp J. 2014;8(1):39-49. https://doi.org/10.2174/1874447801408010039.
33.
Mohammadfam I, Karami Naserkhani R, Soltanian AR. The analysis of deaths caused by driving accidents in Ilam province, western Iran and the related factors by using the method of time series. Int J Occup Hyg. 2016;8(4):200-7.
34.
Khorshidi A, Ainy E, Hashemi Nazari SS, Soori H. Temporal Patterns of Road Traffic Injuries in Iran. Arch Trauma Res. 2016;5(2). e27894. [PubMed ID: 27703958]. [PubMed Central ID: PMC5037289]. https://doi.org/10.5812/atr.27894.
35.
Izadi N, Khoram Dad M, Jamshidi P, Zanganeh AR, Shafiei J, Firouzi A. Epidemiological Pattern and Mortality Rate Trend of Road Traffic Injuries in Kermanshah Province (2009-2014). J Community Health Res. 2016;5(3):158-68.
36.
Hamzeh B, Najafi F, Karamimatin B, Ahmadijouybari T, Salari A, Moradinazar M. Epidemiology of traffic crash mortality in west of Iran in a 9 year period. Chin J Traumatol. 2016;19(2):70-4. [PubMed ID: 27140212]. [PubMed Central ID: PMC4897842]. https://doi.org/10.1016/j.cjtee.2015.12.007.
37.
Sarbaz M, Kimiafar K, Khadem Rezaiyan M, Banaye Yazdipour AR. Epidemiology of transport accidents based on international statistical classification of diseases (ICD-10) in Mashhad, Iran. Int Electron J Med. 2018;7(1):23-9. https://doi.org/10.31661/iejm801.
38.
Rad M, Martiniuk AL, Ansari-Moghaddam A, Mohammadi M, Rashedi F, Ghasemi A. The Pattern of Road Traffic Crashes in South East Iran. Glob J Health Sci. 2016;8(9):149-58. [PubMed ID: 27157159]. [PubMed Central ID: PMC5064071]. https://doi.org/10.5539/gjhs.v8n9p149.
39.
World Health Organization. World report on road traffic injury prevention. Geneva: World Health Organization; 2004, [cited 2022]. Available from: https://www.who.int/publications/i/item/world-report-on-road-traffic-injury-prevention.
40.
Ackaah W, Apuseyine BA, Afukaar FK. Road traffic crashes at night-time: characteristics and risk factors. Int J Inj Contr Saf Promot. 2020;27(3):392-9. [PubMed ID: 32588731]. https://doi.org/10.1080/17457300.2020.1785508.
41.
Ramadani N, Zhjeqi V, Berisha M, Hoxha R, Begolli I, Salihu D, et al. Public Health Profile of Road Traffic Accidents in Kosovo 2010-2015. Open Access Maced J Med Sci. 2017;5(7):1036-41. [PubMed ID: 29362641]. [PubMed Central ID: PMC5771275]. https://doi.org/10.3889/oamjms.2017.214.
42.
Yousefifard M, Toloui A, Ahmadzadeh K, Gubari MIM, Madani Neishaboori A, Amraei F, et al. Risk Factors for Road Traffic Injury-Related Mortality in Iran; a Systematic Review and Meta-Analysis. Arch Acad Emerg Med. 2021;9(1). e61. [PubMed ID: 34580659]. [PubMed Central ID: PMC8464012]. https://doi.org/10.22037/aaem.v9i1.1329.
43.
Sadeghi-Bazargani H, Sadeghpour A, Lowery Wilson M, Ala A, Rahmani F. Developing a National Integrated Road Traffic Injury Registry System: A Conceptual Model for a Multidisciplinary Setting. J Multidiscip Healthc. 2020;13:983-96. [PubMed ID: 33061404]. [PubMed Central ID: PMC7520136]. https://doi.org/10.2147/JMDH.S262555.
44.
Marin S, Pourasghar F, Moghisi AR, Samadirad B, Haddadi M, Khorasani-Zavareh D, et al. Development and psychometric evaluation of data collection tools for Iranian integrated road traffic injury registry: Registrar-station data collection tool. Arch Trauma Res. 2019;8(3):170-6. https://doi.org/10.4103/atr.atr_40_18.
45.
Fathollahi S, Saeedi Moghaddam S, Rezaei N, Jafari A, Peykari N, Haghshenas R, et al. Prevalence of behavioural risk factors for road-traffic injuries among the Iranian population: findings from STEPs 2016. Int J Epidemiol. 2019;48(4):1187-96. [PubMed ID: 30843066]. https://doi.org/10.1093/ije/dyz021.
46.
Khodadadi-Hassankiadeh N, Rad EH, Koohestani HS, Kouchakinejad-Eramsadati L. The Pattern of Road Accidents in Fog and the Related Factors in North of Iran in 2014-2018 . Durham, North Carolina: Research Square; 2020, [cited 2022]. Available from: https://www.researchsquare.com/article/rs-73501/v1.
47.
Delavary M, Ghayeninezhad Z, Lavallière M. Evaluating the Impact of Increased Fuel Cost and Iran’s Currency Devaluation on Road Traffic Volume and Offenses in Iran, 2011–2019. Safety. 2020;6(4):49. https://doi.org/10.3390/safety6040049.
48.
Delavary Foroutaghe M, Mohammadzadeh Moghaddam A, Fakoor V. Impact of law enforcement and increased traffic fines policy on road traffic fatality, injuries and offenses in Iran: Interrupted time series analysis. PLoS One. 2020;15(4). e0231182. [PubMed ID: 32302374]. [PubMed Central ID: PMC7164613]. https://doi.org/10.1371/journal.pone.0231182.
49.
Rahimi H, Hashemi Nazari SS, Soori H, Motevalian SA, Momeni E, Azar A. Traffic Police Effectiveness and Efficiency Evaluations, an Overview of Methodological Considerations. Arch Trauma Res. 2017;6(1). e36927. https://doi.org/10.5812/atr.36927.
50.
Safarzadeh M, Bagheri R. [Comparative studies of traffic fines by traffic police in Iran and other countries]. Rahvar. 2012;9(17):59-74. Persian.
51.
Shams M, Rahimi-Movaghar V. Risky driving behaviors in Tehran, Iran. Traffic Inj Prev. 2009;10(1):91-4. [PubMed ID: 19214883]. https://doi.org/10.1080/15389580802492280.
52.
Tavolinejad H, Malekpour MR, Rezaei N, Jafari A, Ahmadi N, Nematollahi A, et al. Evaluation of the effect of fixed speed cameras on speeding behavior among Iranian taxi drivers through telematics monitoring. Traffic Inj Prev. 2021;22(7):559-63. [PubMed ID: 34424783]. https://doi.org/10.1080/15389588.2021.1957100.
53.
de Winter JCF, Dodou D. National correlates of self-reported traffic violations across 41 countries. Pers Individ Differ. 2016;98:145-52. https://doi.org/10.1016/j.paid.2016.03.091.
54.
Antin J. Design of the In-Vehicle Driving Behavior and Crash Risk Study: In Support of the SHRP 2 Naturalistic Driving Study. Washington, DC: Transportation Research Board; 2011.
55.
Kavousi A, Moradi A, Soori H, Rahmani K. Environmental factors influencing the distribution of pedestrian traffic accidents in Iran. Arch Trauma Res. 2020;9(1):8-15. https://doi.org/10.4103/atr.atr_76_19.
56.
James G, Witten D, Hastie T, Tibshirani R. An introduction to statistical learning. New York, NY: Springer; 2013.
57.
Ramsay JO; Silverman. Functional Data Analysis. New York, NY: Springer; 2005. https://doi.org/10.1007/b98888.
58.
Stasinopoulos D, Rigby RA. Generalized Additive Models for Location Scale and Shape (GAMLSS) inR. J Stat Softw. 2007;23(7):1-46. https://doi.org/10.18637/jss.v023.i07.
59.
Banks D, Persaud B, Lyon C, Eccles K, Himes S. Enhancing Statistical Methodologies for Highway Safety Research – Impetus from FHWA. McLean, VA; 2014. Contract No.: FHWA-HRT-14-081.
60.
Donnell E, Hanks E, Porter RJ, Cook L, Srinivasan R, Li F, et al. The Development of Crash Modification Factors: Highway Safety Statistical Paper Synthesis. McLean, VA; 2020. Contract No.: FHWA-HRT-20-069.
61.
Lohr S. Measuring Crime: Behind the Statistics. New York: Chapman and Hall/CRC; 2019. https://doi.org/10.1201/9780429201189.

comments

Investigation of the Hourly and Spatial Patterns of Traffic Offenses During March-April 2019 in Iran Using Bivariate Generalized Additive Models and Integrated Nested Laplace Approximation

Abstract

Background:

Objectives:

Materials and Methods:

Results:

Conclusions:

Keywords

1. Background

2. Objectives

3. Materials and Methods

3.1. Population and Dataset

3.2. Statistical Analysis

3.2.1. Testing the Multivariate Normal Distribution

3.2.2. Correlation Tests

3.2.3. Generalized Additive Model

3.2.4. Spatial Data Analysis

4. Results

Descriptive Statistics a

Mean Squared Error and Correlation Between Observed Values and Predicted Values by Provinces in Three Generalized Additive Models

Estimated number of speeding (blue) and unsafe distance (red) offenses in A, Gilan; and B, Sistan and Balouchestan, Iran

Mean prediction of A, speeding; and B, unsafe distance rates (within 0 (yellow) and 1 (red))

5. Discussion

Bar chart (green) of highway speed limit (km/h) and line chart (red) of speeding traffic fines (euro) by countries

5.1. Conclusions

References

Cookie Setting

Descriptive Statistics ^a