1. Background
Cerebral palsy (CP) consists of a heterogeneous group of non-progressive clinical syndromes that is caused by abnormal development of the brain and is the most common cause of physical disability in children (1-4). Despite medical and technological progresses in neonatal and prenatal intensive care in the past two decades, movement, and/or cognitive and/or behavioral disorders are still a dilemma in children (5). In general population, the prevalence of CP was reported 1.5 to 2.5 per 1000 live births (6-8). The etiology of CP is multi-factorial (9) and various, and usually arises from a series of causal pathways (7, 10).
Some risk factors for cerebral palsy were identified by investigators such as: low birth weight, premature birth, multiple births, infections during pregnancy, medical conditions of the mother, birth complications, brain infections, injury, asphyxia, preterm delivery, and multiple fetuses (7, 10-12). It is mentioned that having a risk factor does not mean that an infant will have CP (3, 4), but the presence of some risk factors will increase the chance of it (9, 10), i.e., more often multiple risk factors lead to CP (10).
In the most of studies, the risk factors of CP were recognized and reported but the interaction terms of those risk factors were not recognized. The interaction terms effects are of consequence for doctors and therapists and so identification of these terms is of great importance.
Regression analysis provides a way to identify the interaction terms between the risk factors. In the case of a binary response variable, Logistic regression can be used to explain the relationship between the risk factors and response variable (13). But when the independent variables are too large, logistic regression is not efficient to identify interactions. In such situations, penalized logistic regression (PLR), multifactor dimensionality reduction (MDR), Logic regression (LR) approach and classification regression (CR) methods can be used (13-17). This study, the first known study in Iran, adds to the existing information and highlights interaction between main factors. The main purpose of this study is to detect interaction terms effects for risk factors of CP children by PLR, MDR, LFS, and CR methods.
2. Methods
2.1. Data Source
This was a cross-sectional study in which the data of 225 children aged 1 - 6 years was used. This study was approved by university of social welfare and rehabilitation sciences’ ethics committee (code IR.USWR.REC.1394.190). All data was gathered over 12 months, March 2008 to February 2009, in Tehran. 112 subjects with documented CP entered the study. These children were referred from health care centers, located in the eastern and northern parts of the city of Tehran, to Asma comprehensive rehabilitation center as a referral center for the city of Tehran. In addition 113 subjects, who were apparently healthy, i.e. without CP, were randomly selected. “These children had attended only for well-being check-ups (as the control group), and were examined in the same health-care centers by the research team” (5).
2.2. Variables
These related factors of perinatal and neonatal, as the risk factors of CP in children, were collected and used: gender, breech birth, neonatal respiratory disorders, jaundice, sepsis, history of illness, parental consanguinity, premature rupture of membrane (PROM), history of infertility, multiple birth in a pregnancy, previous pregnancies, vaginal bleeding, asphyxia, SGA, preterm delivery (gestational age 37 weeks or less), risky delivery (the first delivery or more than 4 deliveries), history of abortion, vaginal delivery or cesarean delivery, maternal age at delivery (risks: < 16 or > 40 years).
2.3. Statistical Methods
PLR, MDR, LR and CR methods were used to detect interactions. Data analysis was carried out with the R3.2.2 software.
2.3.1. Penalized Logistic Regression
PLR can be considered as generalized regression model which finds interactions with the large number of variable. In this case, the logistic regression criterion is used by combining with a penalization of the L2-norm of the coefficients. “The quadratic penalty makes it possible to code each level of a factor by a dummy variable, yielding coefficients with direct interpretations. This coding method cannot be applied to regular logistic regression because the dummy variables representing a factor are perfectly collinear” (13). In this method, because of avoiding over-fitting, a penalty on large fluctuations is imposed in the process of parameters estimation:
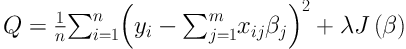
where y is a vector of dependent variables; x is a matrix of independent variables; β is a m × 1 matrix of parameters; λ is tuning parameter; and J(β) is penalty term (13, 17).
2.3.2. Multifactor Dimensionality Reduction
The MDR is a nonparametric method, as an alternative to logistic regression, to detect the interactions of main effects even if the main effects are statistically insignificant. So, this is a weakness of this approach. However, this method considers all combinations of potentially interaction terms (16) and will be able to detect high-order interaction terms (such as two-way and/or three-way interactions, etc.) (17, 18). The MDR method creates a measure of accuracy and then the best model is selected based on the highest accuracy. It is expected that this model perform well in terms of prediction and assessment of internal validation measures (19, 20). For comparing different interactions terms (combination of variables), balanced accuracy (BA) is used as
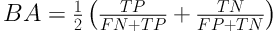
where FP, FN, TP, TN represent the number of false positives, false negatives, true positives, and true negatives, respectively. Indeed BA is the arithmetic mean of sensitivity and specificity (21).
2.3.3. Logic Regression
LR is a (generalized) regression methodology that is applied to detect interaction terms between covariates, especially, when most/all of the covariates are binary. In the LR, we are interested in finding the binary variables which resulting Boolean combinations of initial binary covariates. These new covariates, new combinations, will be entering in the regression model to get the best fit. The LR model is defined as
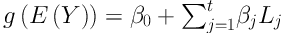
where Y is response variable, β0 and βj are parameters, and Lj is Boolean combination (logic term) of the covariates. In this model, logic terms must be determined and parameters must be estimated simultaneously (14). In this case, a single-tree approach of logic regression was used to detect interaction terms. A large value of variable importance measure (VIM) means a high importance of a particular interaction, whereas a value of about zero means no importance for it (22).
2.3.4. Classification Regression Methods
CR method is one of the most powerful, non- parametric, and yet simple powerful statistical method to determine the most important covariates, and to visualize the important associations and also to find the accurate prediction of outcome (15). Methods which will be used in this sense are: classification and regression tree (CART), AdaBoost, Bagging, and C 4.5 algorithm. These methods, also, will detect the existing interaction between covariates.
3. Results
The average weight of the children at birth was 2491.94 ± 887.13 and 3101.77 ± 542.83 with medians of 2500 and 3150 grams for CP and non CP group respectively. The average gestational age was 35.66 ± 3.78 and 39.81 ± 1.32 with medians of 38 and 40 weeks for CP and non CP group respectively. 47.1% of the studied children were male. In total, 14.7 % of children presented with respiratory disorders, 24.4% with jaundice, 14.7% with sepsis, 17.8% with history of illness, 69.8% with consanguinity, 9.3% with PROM, 4.9% with adjuvant treatment of infertility, 4.9 % with multiple birth in a pregnancy, 7.1% vaginal bleeding, 50.2% with asphyxia, 20.9% with SGA, 19.6% with preterm delivery, 1.3% with high risk delivery, 17.3% with a history of abortion, 19.6% with previous pregnancy, 70.7% with vaginal delivery and 7.6% of maternal risky age (Table 1). The relation between these risk factors and response variable was examined by chi-square and Fisher exact tests. The results of the chi-square test showed that neonatal respiratory disorders (P < 0.001), jaundice (P = 0.040), neonatal infant (P < 0.001), history of illness (P = 0.001), history of consanguinity (P < 0.001), PROM (P = 0.003), adjuvant treatment of infertility (P = 0.028), multiple birth in a pregnancy (P = 0.001), asphyxia (P < 0.001), preterm delivery (P < 0.001), have a significant relationship with CP whereas with ordinary logistic regression analysis, only history of illness (P = 0.002 and OR = 0.03) and asphyxia (P < 0.001 and OR = 127.579) variables were significant.
| Variables | Control, N = 113 | Case, N = 112 | P Valueb |
|---|---|---|---|
| Male gender | 47 (20.9) | 59 (26.2) | 0.125 |
| Breech birth | 4 (1.8) | 4 (1.8) | 1.000 |
| Respiratory disorders | 2 (0.9) | 31 (13.8) | < 0.001 |
| Jaundice | 21 (9.3) | 34 (15.1) | 0.058 |
| Sepsis | 5 (2.2) | 28 (12.4) | < 0.001 |
| History of illness | 30 (13.3) | 10 (4.4) | 0.001 |
| Consanguinity | 50 (22.2) | 107 (47.6) | < 0.001 |
| PROM | 4 (1.8) | 17 (7.6) | 0.006 |
| Adjuvant treatment of infertility | 2 (0.9) | 9 (4.0) | 0.061 |
| Multiple birth | 0 (0.0) | 11 (4.9) | 0.002 |
| Vaginal bleeding | 6 (2.7) | 10 (4.4) | 0.426 |
| Asphyxia | 23 (10.2) | 90 (40.0) | < 0.001 |
| SGA | 19 (8.4) | 28 (12.4) | 0.178 |
| Preterm delivery | 3 (1.3) | 41 (18.2) | < 0.001 |
| High risk delivery | 0 (0.0) | 3 (1.3) | 0.242 |
| History of abortion | 17 (7.6) | 22 (9.8) | 0.462 |
| Previous pregnancy | 17 (7.6) | 27 (12.0) | 0.122 |
| Vaginal delivery | 64 (28.4) | 95 (42.2) | < 0.001 |
| Maternal age (< 16 or > 40 y) | 6 (2.7) | 11 (4.9) | 0.304 |
Characteristics of Children with and Without CP, Based on Their Risk Factorsa
For identifying the interactions by PLR, first, the optimal model based on the BIC criterion and with different values of (tuning parameter) was evaluated. Then, with smallest deviation criterion was considered as a tuning parameter. The value was equal to 0.005. The identified main and interaction effects, from PLR model with forward step-wise and forward stage-wise procedure, are reported in Table 2. The main effects of asphyxia (P < 0.001), consanguinity (P = 0.003), preterm delivery (P = 0.002), history of illness (P = 0.001) were significant effects on CP. In the forward stage-wise procedure, the main effects of asphyxia (P < 0.001), consanguinity (P < 0.001) and also interaction terms of preterm delivery × consanguinity (P = 0.040), history of illness × consanguinity (P < 0.002) had significant relationship with CP.
| Variables | Coefficient | SE | P Value |
|---|---|---|---|
| Intercepta | 9.58 | 2.61 | < 0.001 |
| Asphyxia | 4.28 | 0.71 | < 0.001 |
| Consanguinity | 7.36 | 2.48 | 0.030 |
| Preterm delivery | 7.59 | 2.46 | 0.020 |
| History of illness | -2.95 | 0.90 | 0.010 |
| High risk delivery | 5.14 | 3.78 | 0.174 |
| Interceptb | 6.21 | 1.19 | < 0.001 |
| Asphyxia | 3.50 | 0.59 | < 0.001 |
| Consanguinity | 4.57 | 1.12 | < 0.001 |
| Preterm delivery × consanguinity | 6.52 | 3.17 | 0.040 |
| History of illness × consanguinity | -2.75 | 0.88 | 0.002 |
| Gender × preterm delivery × consanguinity | 1.65 | 3.74 | 0.660 |
Estimated Penalized Logistic Regression Coefficients with Forward Step-Wise and Stage-Wise Procedure
For analyzing the data with MDR, cross validation and 3-way split methods were used to identify the more important compounds.
The results are summarized in Table 3. Both methods showed that the interaction of asphyxia × consanguinity × preterm delivery had the most accuracy, and then the MDR procedure with three-way interaction was fitted to the data. Also, Table 3 shows the identified interaction terms based on balance accuracy. The first compound, i.e. asphyxia × consanguinity × preterm delivery, has higher balance accuracy and hence was detected as an important interaction term. This interaction means that the effect of consanguinity on CP is not equal in the different levels of asphyxia × preterm delivery.
| Number of Interactions | Final Model with 3-Way Split | Training Accuracy | Testing Accuracy | Validation Accuracy |
|---|---|---|---|---|
| k = 4 | Asphyxia × consanguinity × preterm delivery | 97.83 | 91.07 | 82.45 |
| k = 3 | Asphyxia × consanguinity | 87.82 | 91.96 | 85.83 |
| k = 2 | Asphyxia × consanguinity | 86.43 | 92.31 | 90.38 |
| Number of interactions | Final model with cross validation | Classification accuracy | Prediction accuracy | |
| k = 4 | Asphyxia × consanguinity × preterm delivery | 92.13 | 91.92 | |
| k = 3 | Asphyxia × consanguinity × preterm delivery | 92.15 | 92.28 | |
| k = 2 | Asphyxia × consanguinity | 89.32 | 89.03 | |
| Top 5 models identified by MDR method with the best testing accuracy | Balance accuracy | |||
| Asphyxia × consanguinity × preterm delivery | 92.145 | |||
| Asphyxia × consanguinity × respiratory disorders | 90.459 | |||
| Sepsis × asphyxia × consanguinity | 90.001 | |||
| Consanguinity × PROM × asphyxia | 90.001 | |||
| Consanguinity × multiple birth × asphyxia | 89.897 | |||
The MDR Fit Using Three-Way Split and Cross Validation Methods
In LR approach, the most logical important compounds on CP based on VIMsingle index were reported. In this case, Asphyxia × consanguinity × history of illness compound (VIM = 8.00) was most important logical compound. Other identified logical compounds were consanguinity×preterm delivery (VIM = 1.70), history of illness × consanguinity × PROM × asphyxia (VIM = 1.60), consanguinity × asphyxia (VIM = 1.55), consanguinity × PROM × asphyxia (VIM = 0.55), PROM × SGA (VIM = 0.55).
In addition, the result of stepwise logistic regression analysis based on the risk factors and detected logical compounds showed that two logical compounds (history of illness × consanguinity × PROM × asphyxia, and consanguinity × PROM × asphyxia) were significant. For completing the analysis, the significant variables in the ordinary logistic regression without any interactions and these two logical compounds, were modeled and asphyxia variable with two mentioned compounds (P < 0.001) remained in the model.
Finally, the consequences of the AdaBoost and Bagging methods, C4.5 algorithm, and CART are reported in Table 4. Then the performance of these methods with four criteria (sensitivity, specificity, and error as well as Matthew’s correlation coefficient (MCC)), were compared with the 10 stages cross-validation method. The AdaBoost method with lower error (0.06) and higher specificity and sensitivity (0.94 and 0.95, respectively) had a better performance than other methods (Table 5).
| Method | Interactions |
|---|---|
| Adaboost | |
| 2 way | Consanguinity × gender |
| Previous pregnancy × vaginal delivery | |
| 3 way | Consanguinity × preterm delivery × gender |
| Preterm delivery × history of illness × asphyxia | |
| Consanguinity × asphyxia × gender | |
| History of illness × gender × SGA | |
| Sepsis × asphyxia × SGA | |
| History of illness × asphyxia × gender | |
| Preterm delivery × vaginal delivery × asphyxia | |
| Bagging | |
| 2 way | Consanguinity × asphyxia |
| 3 way | Consanguinity × preterm delivery × asphyxia |
| C4.5 algorithm | |
| 2 way | Asphyxia × preterm delivery |
| 4 way | Asphyxia × consanguinity × history of illness × preterm delivery |
| CART | |
| 2 way | Asphyxia × consanguinity |
Detected Interactions by AdaBoost, Bagging, C4.5 Algorithm, CART Methodsa
| Method | Sensitivity | Specificity | Error | MCC |
|---|---|---|---|---|
| AdaBoost | 0.941 ± 0.029 | 0.951 ± 0.030 | 0.06 ± 0.006 | 0.887 ± 0.028 |
| Bagging | 0.832 ± 0.027 | 0.909 ± 0.029 | 0.135 ± 0.007 | 0.737 ± 0.025 |
| C4.5 algorithm | 0.892 ± 0.030 | 0.927 ± 0.029 | 0.095 ± 0.009 | 0.813 ± 0.029 |
| CART | 0.856 ± 0.030 | 0.894 ± 0.028 | 0.115 ± 0.010 | 0.769 ± 0.030 |
Sensitivity, Specificity, and Error in AdaBoost, Bagging, C4.5 Algorithm, and CART Methodsa
4. Discussion
In many epidemiological studies to investigate the relation of risk factors with a special case like presence or absence of a disease, as a dependent variable, logistic regression model was used. If the numbers of dependent variables were large, determining and identifying the interaction becomes difficult or even impossible. In this study, PLR, MDR, LR, and CR models were used to detect interaction terms.
In several studies, improvement of these models has been reported. Park and Hastie have used the PLR and MDR models to determine interaction, gene-gene and gene-environment, terms in blood pressure and Ladder cancer data (13). Sun and Wang have proposed the PLR model for genetic data and showed that this model can be used when data is correlated within a group (18). Stoknes et al. in a study on the Norwegian children with CP disease have identified several interaction terms (preterm birth × induction, maternal disease × preterm birth, maternal disease × premature birth, maternal disease × induction, maternal disease × low 5-minutes Apgar score) between related risk factors. The only significant interaction was reported as maternal disease × preterm birth. In addition, they reported that when the number of risk factors increases, the risk for CP will increase (23). O’Callaghan et al. have not found interaction between SNPs and epidemiologic risk factors for CP outcome. Finally, they have suggested more studies to assess interaction between them (24). Gao et al. in a meta-analysis study showed that maternal age (≥ 35 years), multiple pregnancy, and medicine use in early pregnancy, harmful environment, recurrent vaginal bleeding during pregnancy and pregnancy-induced hypertension were the risk factors for CP (25). Consanguinity was reported as major risk factor in several studies in southwest Asia (26-29). Studies showed that the consanguinity was associated with complex disorders (27) and increases susceptibility to multifactorial diseases (28). In addition, it is considered as a factor of higher reading disabilities (29, 30) and the cause of developmental problems (31). They have not reported any interaction terms between risk factors.
In most studies of CP no interaction between the risk factors was reported. Models without any interactions occur, when the number of risk factors is large and so determining the interactions will be difficult or even impossible. However, based on used method in this study, consanguinity, preterm birth, and asphyxia have had the most interaction with other risk factors. In this scene, consanguinity is a cultural factor and also important to investigate. One of the limitations of this study was the sample size in CP group. The cultural, local and available health system, e.g. NICU can probably affect the proportion of consanguinity and asphyxia and also homogeneity of other risk factors in this sample. So the researchers should pay attention to this issue, conduct their research using larger sample size in other CP population studies.
4.1. Conclusions
Detection and identification of some interaction terms between risk factors of CP using PLR, MDR, LR and CR models were most important results of this study and specially, there was an interaction between the consanguinity factor and other factors. These models have played an important role in the identification of interaction terms in real data (16-18, 22, 32) and simulation data set (14, 17, 22, 33). Such statistical methods have the ability of detecting risk factors interactions of diseases, such as CP. It is mentioned that this study is the beginning for a comprehensive discussion on interaction terms between risk factors in CP patients. Our results can be used by therapists and clinicians to design a preventive strategy for these patients.
